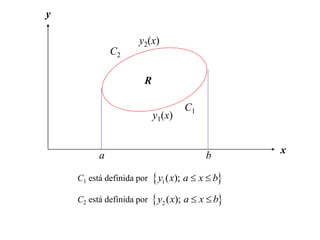
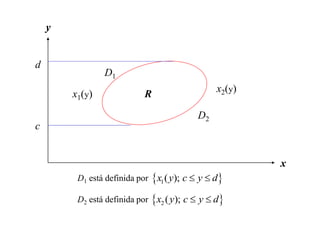
El documento presenta una demostración del Teorema de Green para una región suave. Primero, proyecta la región sobre el eje x e integra con respecto a y. Luego, proyecta la región sobre el eje y e integra con respecto a x. Al combinar estas dos ecuaciones, se obtiene el famoso teorema de Green.

1. Esbozo de demostración del Teorema de Green para una
región suave.
C
R
M L
Ldx M dy dxdy
x y
 
 
  
 
 
 
 
Ñ
Permitida su reproducción, libre y sin fines de lucro

2. x
y
a b
R
y1(x)
y2(x)
Sea C la curva cerrada que determina la frontera de la región R.
C1
C2
Se forma la curva C1, descrita por la función y1( x ); y la curva C2
descrita por la función y2( x ).
Proyectaremos la región R sobre el eje X

3. x
y
a b
R
y1(x)
y2(x)
C1
C2
C1 está definida por  
1( );
y x a x b
 
C2 está definida por  
2 ( );
y x a x b
 

4. x
y
a b
R
y1(x)
y2(x)
C1
C2
Vamos a calcular la integral
( , )
R
L x y
dxdy
y



2
1
( )
( )
( , )
y x
b
a y x
L x y
dy dx
y
 

  
 

 
 
( , )
R
L x y
dxdy
y


  
2 1
( , ( )) ( , ( ))
b
a
L x y x L x y x dx
 

2 1
( , ( )) ( , ( ))
a b
b a
L x y x dx L x y x dx
  
  2 1
C C
Ldx Ldx
  
 
Ñ Ñ C
Ldx
 
Ñ
( , )
C
R
L x y
Ldx dxdy
y

 

 
Ñ

5. x
y
c
d
R
x1(y)
x2(y)
Sea C la curva cerrada que determina la frontera de la región R.
D1
D2
Se forma la curva D1, descrita por la función x1( y ); y la curva D2
descrita por la función x2( y ).
Ahora proyectaremos la región R sobre el eje Y

6. D1 está definida por  
1( );
x y c y d
 
D2 está definida por  
2 ( );
x y c y d
 
x
y
c
d
R
x1(y)
x2(y)
D1
D2

7. x
y
c
d
R
x1(y)
x2(y)
D1
D2
Vamos a calcular la integral
( , )
R
M x y
dx dy
x



2
1
( )
( )
( , )
x x
d
c x x
M x y
dx dy
x
 

  
 

 
 
( , )
R
M x y
dx dy
x


  
2 1
( ( ), ) ( ( ), )
d
c
M x y y M x y y dy
 

2 1
( ( ), ) ( ( ), )
d c
c d
M x y y dy M x y y dy
 
  2 1
D D
M dy M dy
 
 
Ñ Ñ C
M dy
 
Ñ
( , )
C
R
M x y
M dy dxdy
x



 
Ñ

8. x
y
R
C
De este modo obtenemos el famoso teorema de Green
C
R
M L
Ldx M dy dxdy
x y
 
 
  
 
 
 
 
Ñ
( , )
C
R
L x y
Ldx dxdy
y

 

 
Ñ
( , )
C
R
M x y
M dy dxdy
x



 
Ñ