Este documento trata sobre el cálculo de integrales dobles, triples e integrales de línea y superficie. Incluye temas como integrales dobles en coordenadas polares y esféricas, teoría de campos escalares y vectoriales, divergencia, rotacional y laplaciana. También presenta los teoremas de Green, Stokes y el teorema de la divergencia.

1. CONTENIDO
1. Integrales dobles
2. Integrales dobles en coordenadas polares
3. Integral triple
4. Coordenadas esfericas
5. Coordenadas cilindricas
6. Teoria de campos escalares
7. Teoria de campos vectoriales
8. Integral de linea
9. Integral de superficie
10. Divergencia
11. Rotacional
12. Laplaciana
13. Teorema de Green
14. Teorema de Stokes
15. Referencias bibliograficas
1

2. INTRODUCCION
La matem´atica es la ciencia que se ocupa de describir y analizar las cantidades, el espacio y las
formas, los cambio y las relaciones, asi como la incertidumbre. Si miramos a nuestro al rededor
vemos que esos componentes estan presentes en todos los aspectos de la vida de las personas,
en su trabajo, en su que hacer diario, en los medios de comunicaci´on, etc.
Las matem´aticas son universales: Los resultados que se obtienen son aceptados por toda la
comunidad internacional, lo que no quiere decir que los metodos que se han utilizado histori-
camente sean iguales: Lo que si son universales son las actividades, muchas entrocadas con la
cultura de los pueblos, que han impulsado el conocimiento matematico. De esta manera habla-
mos de: Contar, localizar, medir, explicar, jugar, etc.
En el presente trabajo, se detallaran el estudio de los campos vectoriales (funciones que asignan
vectores a puntos en el espacio). En particular definimos las integrales de linea (que pueden
utilizarse para determinar el trabajo realizado por un campo de fuerza al mover un objeto a
lo largo de una curva). Mas tarde, definimos las integrales de superficie (que pueden emplearse
a fin de calcular la razon de flujo de fluido sobre una superficie). Las conexiones entre estos
nuevos tipos de integrales y las integrales sencillas, dobles y triples que hemos estudiado, se
establecen en las versiones para dimensiones superiores del teorema fundamental del calculo:
de Green, de Stokes y de la divergencia.
2

3. DEDICATORIA
Primeramente a Dios por haberme permitido llegar hasta este punto y haberme dado salud,
ser el manantial de vida y darme lo necesario para para seguir adelante dia a dia para lograr
mis objetivos ademas de su infinita bondad y amor.
A mi madre por haberme apoyado en todo momento, por sus consejos, sus valores, por la
motivacion constante que me ha permitido ser una persona de bie, pero mas que nada por su
amor. A mi padre por los ejempls de perseverancia y constancia que lo caracterizan y que me
ha influido siempre, por el valor mostrado para salir adelante y por su amor.
A mi maestro por su gran apoyo y motivacion para la culminacion de nuestros estudios pro-
fesionales, por su apoyo ofrecido en este trabajo, por haberme transmitido los conocimientos
obtenidos y haberme llevado paso a paso en el aprendizaje.
3

4. 1. INTEGRALES DOBLES
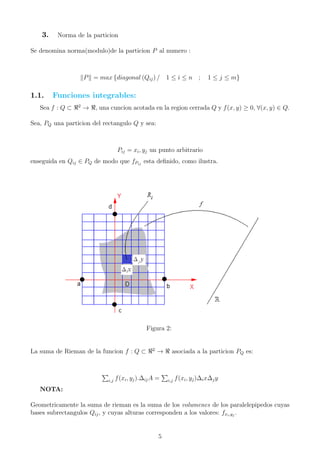
1. Toda particion P del rectangulo Q, divide en nm subrectangulos de la forma:
Qij = [xi−1, xi] × [yj−1, yj] a Q
esto es:
P = {Qij = [xi−1, xi] × [yj−1, yj] = / 1 ≤ i ≤ n ; 1 ≤ j ≤ m}
2. El area de cada sub rectangulo Qij:
para: i : 1, 2, 3, ..., n
j : 1, 2, 3, ..., n
se denota por ∆ijA = ∆ix.∆jy
Ademas se verifica que : ij ∆ijA = (b − a)(c − d)
EN EFECTO:
Figura 1:
4

5. 3. Norma de la particion
Se denomina norma(modulo)de la particion P al numero :
P = max {diagonal (Qij) / 1 ≤ i ≤ n ; 1 ≤ j ≤ m}
1.1. Funciones integrables:
Sea f : Q ⊂ 2
→ , una cuncion acotada en la region cerrada Q y f(x, y) ≥ 0, ∀(x, y) ∈ Q.
Sea, PQ una particion del rectangulo Q y sea:
Pij = xi, yj un punto arbitrario
enseguida en Qij ∈ PQ de modo que fPij
esta definido, como ilustra.
Figura 2:
La suma de Rieman de la funcion f : Q ⊂ 2
→ asociada a la particion PQ es:
i,j f(xi, yj).∆ijA = i,j f(xi, yj)∆ix∆jy
NOTA:
Geometricamente la suma de rieman es la suma de los volumenes de los paralelepipedos cuyas
bases subrectangulos Qij, y cuyas alturas corresponden a los valores: fxi,yj
.
5

6. Definicion 1. una funcion acotada f : Q ⊂ 2
→ es integrable RIEMAN sobre
la region cerrada Q, si existe un numero v con la propiedad de que , dado
ε > 0, ∃δ > 0/ i,j f(xi, yj)∆ix∆jy − V < ε
Para toda particion PQ, con PQ < δ y toda eleccion del punto Pij = (xi, yj)
para: i : 1, 2, 3, ..., n
j : 1, 2, 3, ..., n
este numero V es llamado INTEGRAL DOBLE de f sobre el conjunto Q y se indica
con el simbolo:
V =
Q
f(x, y)dA = l´ım
PQ →0
i,j
f(xi, yj)∆ix∆jy
Interpretacion geometrica
si f : Q ⊂ 2
→ , es una funcion integrable en Q y f(x, y) ≥ 0, entonces la grafica de
Z = f(x, y) es una superficie que esta encima del plano XY, luego:
Q
f(x, y).dA = v(S)
Es un volumen de un solido S,bajo la superficie Z = f(x, y) y tiene como base la region cerrada
Q.
6

7. EN EFECTO
Figura 3:
Propiedades fundamentales de la integral doble
Si f : Q ⊂ 2
→ , es una funcion integrable en la region cerrada Q, y C ∈ , entonce,
c.f es integrable en la region Q, por tanto:
Q
cf(x, y)dA = c Q
f(x, y)dA
Si, f : Q ⊂ 2
→ , es una funcion integrable.
g : Q ⊂ 2
→ , es una funcion integrable, en la region cerrada Q, entonces, f ± q
es integrable en Q:
Q
[f(x, y) ± g(x, y)] dA = Q
f(x, y)dA ± Q
g(x, y)dA
Si, f : Q ⊂ 2
→ , es una funcion CONTINUA en la region cerrada Q , y Q = Q1 ∪ Q2,
donde Q1 y Q2 son regiones cerradas, entonces:
Q
f(x, y)dA = Q1
f(x, y)dA + Q2
f(x, y)dA
Teorema del valor medio:
Si,f : Q ⊂ 2
→ , es una funcion continua en la region cerrada y acotada Q, entonces
existe un punto (k, r) ∈ Q talque:
Q
f(x, y)dA = f(k, r) Q1
dA = f(k, r).A(Q)
7

8. NO OLVIDAR: funcion continua:
a. fx0 exista
b. l´ımx→x+
0
f (x) f (x) = l´ımx→x−
0
f (x) ⇒ l´ım f (x) = L exista
c. l´ımx→x0 f (x) = f(x0) = L
Figura 4:
8

9. 1.2. Region en R2
sea Q ⊂ 2
, diremos D es una region, si es la union de un conjunto abierto conexo con
algunos, ninguno o todos sus puntos de frontera.
OBSERVACIONES:
Intuitivamente el conjunto conexo es aquel que esta hecho de una sola pieza un conjunto es
simplemente simplemente conexo si puede continuarse hasta reducirse a un punto, esto es:
Figura 5:
Ejemplo 1 si, D =



(x, y) 2
/
√
4 ≤
x=2
x < 2
√
y=x
, 0 ≤
y=1
y < 1
y=0



trazar su representacion
grafica:
Solucion
F1 = {(x, y) 2
/ y = 0, 0 ≤ x < 2}
F2 = {(x, y) 2
/ y = x2
, 0 ≤ x < 1}
F3 = {(x, y) 2
/ y = 1, 1 ≤ x < 2}
F4 = {(x, y) 2
/ x = 2, 0 ≤ y < 1}
9

10. Figura 6:
Ejemplo 2 Sea la region D, trazar su grafica correspondiente
D =



(x, y) 2
/ x2
≤
y=x
y < x
x2=y
, 0 ≤
x=1
x < 1
x=0



F1 = {(x, y) 2
/ x = 0 , y = 0}
F2 = {(x, y) 2
/ y = x2
, 0 ≤ y ≤ 1}
F3 = {(x, y) 2
/ y = x, 0 ≤ y ≤ 1}
F4 = {(x, y) 2
/ x = 1 , y = 1}
Figura 7:
10

11. 1.3. Integrales dobles mediante integrales iteradas
CASO I:
sea f : Q ⊂ 2
→ , una funcion continua e integrable en el rectangulo Q = [a, b] × [c, d],
fijando la variable Y en [c, d] la funcion f depende solo de la variable X, continua en [a, b]
Asi:
A(y) =
b
a
f(x, y)dx; c ≤ y ≤ d ,
es el area de la region transversal, que es la interseccion del plano: y = y0 con el solido S,
que esta debajo de la superficie Z = f(x, y), y por encima de la region Q ⊂ 2
. pensando de
manera intuitiva, sumar todas las secciones transversales, es equivalente a integrar desde y = c,
hasta y = d.Entonces, por el metodo de area de secciones transversales, el volumen del solido
S es la integral doble de: f(x, y) sobre Q
En efecto:
Vs =
Q
f(x, y)dx.dy =
d
c
Aydy =
d
c
b
a
f(x, y)dx dy
Interpretacion Geometrica
Figura 8:
11

12. el argumento anterior es el mismo si consideramos las secciones transversales del solido S
que se obtienen al cortar con planos paralelos al plano Y Z (del tipo x: constante), cuyas areas
estan dadas por:
A(x) =
d
c
f(x, y)dy
Al sumar todas las secciones transversales, integrando A(x) desde x = a hasta x = b, obtenemos
el volumen del solido S, es decir:
Vs =
Q
f(x, y)dx.dy =
d
c
Axdx =
b
a
d
c
f(x, y)dy dx
Figura 9:
CASO II: Integrales dobles de funciones sobre regiones mas generales
ampliamos ahora el concepto de integral doble de una funcion f(x, y) = z, sobre rectangu-
los Q, o rectangulos ms generales en 2
. Estos seran subconjuntos acotados del plano (que
podamos incluir en un rectangulo Q) y las clasificamos en tres tipos:
12

13. Regiones de tipo I
sean ∅1 : [a, b] −→ , funciones de variable real (continuas)
∅2 : [a, b] −→
x [a, b], de modo que: ∅1(x) ≤ ∅2(x); ∀x [a, b]
consideramos la region R1 del plano, dada por:
R1 = (x, y) 2
/ a ≤ x ≤ b ; ∅1(x) ≤ y ≤ ∅2(x)
Figura 10:
El hecho que las funciones : ∅1 y ∅2 sea funciones continuas en el intervalo cerrado [a, b],
garantiza que son acotadas, lo cual a su vez garantiza que son que la region R1 es una region
acotada del plano entonces la integral iterada de: z = f(x, y) sobre la region R1 se puede cal-
cular como:
R1
f(x, y)dx.dy =
R1
f(x, y)dA =
b
a
φ2(x)
φ1(x)
f(x, y)dy dx
R1
f(x, y)dA =
b
a
φ2(x)
φ1(x)
f(x, y)dy.dx
13

14. Regiones de tipo II
sean ∅1 : [c, d] −→
∅2 : [c, d] −→
Dos funciones continuas de variable real, y que pertenece al intervalo [c, d], de modo que
∅1(y) ≤ ∅2(y); ∀x [c, d] consideramos la region R2 del plano definido por:
R2 = {(x, y)/ c ≤ y ≤ d , Ψ1(y) ≤ x ≤ Ψ2(y)}
Nuevamente, por la continuidad de funciones : ∅1 y ∅2 en el intervalo cerrado [c, d] podemos
garantizar que la region R2 es acotada.
Es decir:
L a integral iterda (integral doble) de Z = f(x, y) sobre la region R2 se puede calcular como:
R2
f(x, y)dx.dy =
R2
f(x, y)dA =
d
c
ψ2(y)
ψ1(y)
f(x, y)dx dy
R2
f(x, y)dx.dy =
d
c
ψ2(y)
ψ1(y)
f(x, y)dx.dy
R2 = (x, y) 2
/ c ≤ y ≤ d , Ψ1(y) ≤ x ≤ Ψ2(y)
Figura 11:
14

15. Regiones de tipo III
considerando regiones que se pueden descomponer, por medio de un numero finito de cor-
tes verticales y horizontales, en regiones de tipo 1 o en regiones de tipo 2. casos concretos de
regiones de este tipo se estudiaran en los siguientes ejemplos:
Ejemplo 1 consideramos la region comprendida entre las funciones:
y = 4 − x2
, y = x2
− 4
Solucion
Al trazar las rectas verticales x = −2 y x = 2 la region se puede considerar de manera natural
como una region del tipo 1. hallando las intersecciones entre las parabolas se tiene:
x1 = 2
x2 = −2
Figura 12:
Luego se tiene que la region que limitada
Por la derecha, por la recta x = −2
por la izquierda, por la recta x = 2
por debajo, por la prabola ϕ1(x) = x2
− 4
por encima, por la parabola ϕ2(x) = 4 − x2
Finalmente
15

16. R1
f(x, y)dx.dy =
x2=2
x1=−2
y2φ2(x)
y1φ1(x)
f(x, y)dy dx
1.4. Teorema de Fubini
sea z = f(x, y) una funcion continua, definida sobre una region plana rectangular R.
a.-si se define la region rectangular R mediante a ≤ x ≤ b y g1(x) ≤ y ≤ g2(x) siendo, g1
y g2 funciones continuas en [a, b], entonces:
R
f(x, y)dA =
b
a
g2(x)
g1(x)
f(x, y)dy dx
b.-si se define la region R mediante c ≤ y ≤ d y h1(y) ≤ x ≤ h2(y) siendo h1 y h2 funciones
continuas en [c, d], entonces:
R
f(x, y)dA =
d
c
h2(y)
h1(y)
f(x, y)dx dy
Por lo tanto:
R
f(x, y)dA =
b
a
d
c
f(x, y)dy dx =
d
c
b
a
f(x, y)dx dy
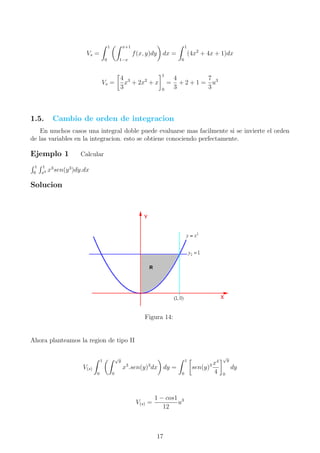
Ejemplo Calcular R
f(x, y)dx.dy
sobre la region D limitada por un triangulo cuyos vertices son: (0, 1) (1, 2) (1, 0)
Figura 13:
16

17. Vs =
1
0
x+1
1−x
f(x, y)dy dx =
1
0
(4x2
+ 4x + 1)dx
Vs =
4
3
x3
+ 2x2
+ x
1
0
=
4
3
+ 2 + 1 =
7
3
u3
1.5. Cambio de orden de integracion
En muchos casos una integral doble puede evaluarse mas facilmente si se invierte el orden
de las variables en la integracion. esto se obtiene conociendo perfectamente.
Ejemplo 1 Calcular
1
0
1
x2 x3
sen(y3
)dy.dx
Solucion
Figura 14:
Ahora planteamos la region de tipo II
V(s)
1
0
√
y
0
x3
.sen(y)3
dx dy =
1
0
sen(y)3 x4
4
√
y
0
dy
V(s) =
1 − cos1
12
u3
17

18. 1.6. Cambio de Variables en integrales dobles
Defincion 1
Una funcion vectorial T de variable vectorial es una correspondencia de un conjunto de vecto-
res A ⊂ n, a un conjunto de vectores, B ⊂ m, es decir, es una transformacion del conjunto
A ⊂ n en el conjunto B ⊂ m
Cuya notacion es:
T : A ⊂ n → B ⊂ m
talque:
T(u1, u2, u3, ...., un) = (x1, x2, x3, ..., xm)
Donde cada xi, i = 1, 2, 3, ..., m son funciones de las variables u1, u2, u3, ..., un es decir:
x1 = x1 (u1, u2, u3, ..., u3)
x2 = x2 (u1, u2, u3, ..., um)
x3 = x3 (u1, u2, u3, ..., um)
xm = xm (u1, u2, u3, ..., um)
EJEMPLOS
Figura 15:
18

19. Figura 16:
Definicion 2
una funcion vectorial de variable vectorial es una correspondencia de un conjunto de vec-
tores, D ⊂ 2, a un conjunto de vectores E ⊂ m
, es decir, es una tranformacion de una
region:D ⊂ 2 en otra region,E ⊂ m
, cuya notacion es:
T : D ⊂ 2 → E ⊂ m
talque
T(u1, u2, u3, ...., un) = (x1, x2, x3, ..., xm)
Donde cada xi, i = 1, 2, 3, ..., m son funciones de las variables u1, u2, u3, ..., un
Esto es:
x1 = f1 (u1, u2, u3, ..., un)
x2 = f2 (u1, u2, u3, ..., un)
x3 = f3 (u1, u2, u3, ..., un)
xm = fm (u1, u2, u3, ..., un)
Ejemplo 1 Dada la transformacion definida por T(u, v) = (2+u−2v, 1+u+v) = (x, y)
D ⊂ 2
= [0, 1] × [0, 1] = {(u, v) 2
/u [0, 1] , v [0, 1]}
Analizar como es la T(D) del cuadrilatero D via la funcion T
19

20. Solucion
Figura 17:
a.- Analizando la imagen del segmento horizontal desde (0,0) hasta (1,0) via la funcion T:
para (0,0) t(0, 0) = (2 + 0 − 2(0), 1 + 0 + 0) = (2, 1)
t(1, 0) = (2 + 1 − 2(0), 1 + 1 + 0) = (3, 2)
Como varia el segmento horizontal desde (0, 0) hasta (1, 0)
para (u, 0) t(u, 0) = (2 + u − 2(0), 1 + u + 0) = (2 + u, 1 + u)
x = 2 + u u = x − u
y = 1 + u u = y − 1
Figura 18:
20

21. 1.7. Continuidad de las transformaciones
Definicion
una transformacion , T : n
→ n
, es una funcion vectorial de variable vectorial, talque:
si, −→u = (u1, u2, u3, ..., un), −→x = (x1, x2, x3, ..., xn). entonces:
−→x = (x1, x2, x3, ..., xn) = T(−→u ) = (f1(−→u ), f2(−→u ), ..., fn(−→u ))
Donde las funciones fi son funciones reales componentes, y xi = fi(−→u ) = fi(u1, u2, ..., un)
que tambien se denota por
xi = xi(−→u ) = xi(u1, u2, ..., un).
Donde las coordenadas xi son funciones reales, llamadas funciones coordenadas de T de n
variables u1, u2, ..., un.
En efecto:
xi = fi : n
→
luego:
x = T(u) = T(u1, u2, u3, ..., un)
= (x1(u), x2(u), x3(u), ..., xn(u))
= (x1(u1, u2, u3, ..., un), x2(u1, u2, u3, ..., un), x3(u1, u2, u3, ..., un), ..., xn(u1, u2, u3, ..., un))
= (f1(u), f2(u), f3(u), ..., fn(u))
PROPOSICION
Una transformacion T ⊂ Rn
→ Rn
se dice que es de CLASE Ck
sobre D, es decir, si to-
das las funciones coordenadas xi(u) = fi(u) son continuas y tiene sus derivadas parciales hasta
el orden k, todas continuas sobre el dominio D
21

22. 1.8. Derivada de la transformacion
Si una transformacion :T : D ⊂ n
→ n
es decir de clase Ck
, entonces todas sus funciones
cordenadas: xi = fi = fi(u) son derivables y por lo tanto existen sus gradientes o derivadas:
f1(u) =
∂f1
∂u1
,
∂f1
∂u2
,
∂f1
∂u3
, ...,
∂f1
∂un
=
∂x1
∂u1
,
∂x1
∂u2
,
∂x1
∂u3
, ...,
∂x1
∂un
fi(u) =
∂fi
∂u1
,
∂fi
∂u2
,
∂fi
∂u3
, ...,
∂fi
∂un
=
∂xi
∂u1
,
∂xi
∂u2
,
∂xi
∂u3
, ...,
∂xi
∂un
DEFINICION
Dada una transformacion r = (f1, f2, f3, ..., fn) de Rn
de clase Ck
, sobre un dominio D
x = T(u) = (f1(u), f2(u), f3(u), ..., fn(u))
Se define la derivada de T en el punto u = (u1, u2, u3, ..., un) ∈ D a la matriz cuadrada
de orden n, definida Por:
T (u) =










f1(u)
f2(u)
f3(u)
.
.
.
fn(u)










=











∂f1(u)
∂u1
∂f1(u)
∂u2
.... ∂f1(u)
∂un
∂f2(u)
∂u1
∂f2(u)
∂u2
.... ∂f2(u)
∂un
.
.
.
∂fn(u)
∂u1
∂fn(u)
∂u2
... ∂fn(u)
∂un











22

23. 1.9. Matriz jacobiana y jacobianos de transformacion
La matriz jacobiana de orden n, derivada de T en un punto u ∈ D Cn
, se llama ma-
triz JACOBIANA de T en u, por ser la matriz cuadrada, a su determinante se le denomina
JACOBIANA de la transformacion T en el punto u y se denota por
J(u) = ∂ (x1, x2, x3, ..., xn) ∂ (u1, u2, u3, ..., un) det |T (u)|
Ejemplo: Sea (x, y) = T(u, v) = (u.cosv, u.senv)
entonces:
J(u, v) = (x, y)(x, y) =
xu xv
yu yv
=
cosv − u.senv
senv u.cosv
cosv − u.senv
senv u.cosv
= u(cos2
v + sen2
v) = u
Ejemplo T(u, v, w) = (x, y, z) = (2u, −3v, 5w)
J(u, v, w) = (x, y, z)(u, v, w) =
xu xv xw
yu yv yw
zu zv zw
=
2 0 0
0 − 3 0
0 0 5
J(u, v, w) = det
2 0 0
0 − 3 0
0 0 5
= −30
Teorema
Sea T : R2
→ R una transformacion, tal que
x = g(u, v)
y = h(u, v)
(x, y) = T(u, v) = (x(u, v), y(u, v))
de clase Ck
sobre un conjunto abierto Ω del plano uv y que T(u, v) es univalente con jacobiano
no nulo:
J(u, v) =
∂(x, y)
∂(u, v)
= 0
Donde ∂(x,y)
∂(u,v)
=
∂x
∂u
∂x
∂v
∂y
∂u
∂y
∂v
J(u, v) = det
∂x
∂u
∂x
∂v
∂y
∂u
∂y
∂v
Sea D ⊂ Ω (⊂ plano UV ) un conjunto cerrado y acotado que tiene area, y sea E = T(D)
en el plano xy la imagen del conjunto D por la transformacion T Entonces, si f(x, y) es
INTEGRABLE sobre E, la funcion f = T(u, v) es integrable sobre D y
E
f(x, y)dxdy =
D
f [x(u, v), y(u, v)] .
∂(x, y)
∂(u, v)
dudv
23

24. Figura 19:
Observacion:
Notese que el factor de correccion es el valor absoluto del Jacobiano o valor absoluto o deter-
minante Jacobiano.
Ejemplo:
Sea D la region limitada por las rectas:
x − 2y = 0 x + y = 4
x − 2y = −4 x + y = 1
Calcular la integral doble R
3xydA
hagamos:
u = x + y = 4 ⇒ u = 4
u = x + y = 1 ⇒ u = 1
v = x − 2y = 0 ⇒ v = 0
v = x − 2y = −4 ⇒ v = −4
Si u = x + y ⇒
x = u − y
y = u − x
v = x − 2y ⇒
x = v + 2y
y = x−v
2
Luego el jacobiano es:
∂(x, y)
∂(u, v)
=
∂x
∂u
∂x
∂v
∂y
∂u
∂y
∂v
=
23 13
13 − 13
= −13
R
3xydA =
D
f [x(u, v), y(u, v)]
∂(x, y)
∂(u, v)
du.dv
R
3 ×
1
9
2u2
− uv − v2 1
3
du.dv
24

25. 2. INTEGRALES DOBLES EN COORDENADAS PO-
LARES
Si (x, y) son las coordenadas cartesianas del plano R2
y (r, θ) son las coordenadas polares
del plano R2
existe una transformacion inyectiva de R2
en R2
definida por:
T : R2
→ R2
(r, θ) → (x, y) = T(r, θ)
Tal que
x = rcosθ
y = rsenθ
0 ≤ r ≤∝
α θ α + 2π
Es decir (x, y) = T(r, θ) = (rcosθ, rsenθ)
Esta transformacion (funcion vectorial de variable vectorial) inyectiva hace corresponder a cada
punto (r, θ) ∈ D un solo punto (x, y) ∈ R = T(D) y viceversa, esto es:
Figura 20:
25

26. Ejemplo 1. Calcular R
arctg y
x
dx.dy sobre la region
R = (x, y) ∈ R2
/ 1 x2
+ y2
≤ 9 x√
3
≤ y ≤
√
3x
Solucion Cambiando a coordenadas polares:
Se sabe que la transformacion a coordenadas polares esta definido por:
x = rcosθ
y = rsenθ
tgθ = y
x
⇒ θ = arctg y
x
x2
= r2
cos2
θ
y2
= r2
sen2
θ
⇒ x2
+ y2
= r2
J(r, θ) =
∂(x, y)
∂(r, θ)
= det


∂x
∂r
∂x
∂θ
∂y
∂r
∂y
∂θ

 = det


cosθ − rsenθ
senθ rcosθ


= r(cos2
θ + sen2
θ) = r
Debemos hallar la region D que es la imagen inversa de la region R en coordenadas pola-
res, mediante T
Es decir hallaremos D = T−1
(R), esto es posible haciendo los cambios de variables en la region
R, asi tenemos
Como x2
+ y2
= r2
⇒
1 ≤ r2
≤ 9
1 ≤ r ≤ 3
Como y = x√
3
⇒ y
x
= 1√
3
⇒ tgθ = 1√
3
⇒ θ1 = π
6
y =
√
3x ⇒ y
x
=
√
3 ⇒ tgθ =
√
3 ⇒ θ2 = π
3
Por lo tanto:
π
6
≤ θ ≤
π
3
26

27. Entonces se ha obtenido la region D en el plano rθ
Figura 21:
R
f(x, y)dx.dy =
D
f(rcosθ, rsenθ) |J(r, θ)| .dr.dθ
=
π
3
π
6
3
1
θrdr.dθ =
π
3
π
6
θ
r2
2
3
1
dθ
=
π
3
π
6
9
2
−
1
2
θdθ = 4
(π
3
)2
2
−
π
6
2
2
= 2
π2
12
⇒ V =
π2
6
u3
3. INTEGRAL TRIPLE
Definicion 1. Se dice que un conjunto S ⊂ R3
es acotado cuando existe un para-
lelepiped rectangular:
R = [a, b] × [c, d] × [e, f] tal que S ⊂ R, el paralelepipedo R puede ser escrito como:
R = (x, y, z) ∈ R3
/a x b, c ≤ y ≤ d, e ≤ z ≤ f
Definicion 2. Una particion de R puede ser escrito de la forma:
P = P1 ×P2 ×P3 = {[xi−1, xi] × [yj−1, yj] × [zk−1, zk] /1 ≤ i ≤ n, 1 ≤ j ≤ m, 1 ≤ k ≤ q}
27

28. Donde
P1 = {x0, ..., xn} es una particion del intervalo [a, b]
P2 = {y0, ..., yn} es una particion del intervalo [c, d]
P2 = {y0, ..., yn} es una particion del intervalo [e, f]
Observaciones
Toda particion P del paralelepipedo R divide en nmq subparalelepipedos de la forma:
Rijk = [xi−1, xi] × [yj−1, yj] × [zk−1, zk] a R
Esto es
P = {Rijk/ 1 ≤ i ≤ n, 1 ≤ j ≤ m, 1 ≤ k ≤ q}
El volumen de cada sub pararalelepipedo se denota por:
∆ijkV = ∆ix ∆jy ∆kz
Se verifica que
ijk ∆ijkV = (b − a)(d − c)(f − e)
Se denomina norma de la particion P al numero.
P = max {diag(Rijk) / 1 ≤ i ≤ n, 1 ≤ j ≤ m, 1 ≤ k ≤ q}
Definicion 2. Una funcion acotada f : S ⊂ R3
→ R es integrable Rieman sobre el
conjunto acotado S, si existe un numero L con la propiedad de que, dado ε > 0, ∃ δ > 0
talque
ijk f(xi, yj, zk)∆ix ∆jy ∆kz − L < ε
Para toda la particion Ps con Ps ≤ δ y toda eleccion del punto Pijk ∈ Rijk, el punto L
es llamado integral triple de f sobre S y se denota con el simbolo.
28

29. S
f(x, y, z).dv =
S
f(x, y, z)dx.dy.dz
Figura 22:
Propiedades de la integral triple
S
kf(x, y, z).dv = k S
f(x, y, z).dv, k = cte
S
f(x, y, z)dv = S1
f(x, y, z)dv + S2
f(x, y, z)dv S = S1 ∪ S2
S
[f(x, y, z) ± g(x, y, z)] dv = S
f(x, y, z)dv ± S
g(x, y, z)dv
OBSERVACION
Sea S ⊂ R3
una region en el espacio tridimensional que sea cerrada y acotada.
Si w = f(x, y, z) es una funcion acotada sobre S la integral triple de f sobre S se define
como.
S
f(x, y, z)dv donde
dv = dz.dy.dx
dv = dz.dx.dy
dv = dy.dx.dz
dv = dy.dz.dx
dv = dx.dz.dy
dv = dx.dy.dz
El orden de estas diferenciales dependera de la forma como se presenta la region S donde debe
observarse quien es el techo y quienes forman el piso.
29

30. 3.1. Integrales triples mediante integrales iteradas
Sea D = {(x, y) ∈ R2
/ a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x)} una region cerrada en el plano XY
donde g1, g2 : [a, b] → R son funciones continuas con g1(x) ≤ g2(x) ∀x ∈ [a, b]
Sean h1(x), h2(x) : D ⊂ R2
→ R funciones continuas en la region cerrada D y que h1(x) ≤
h2(x) ∀x ∈ D
Sea, S = {(x, y, z) ∈ R3
/ a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x), h1(x) ≤ z ≤ h2(x)} una region ce-
rrada en R3
Si f : S ⊂ R3
→ R es una funcion continua en S, entonces la integral iterada de f es:
S
f(x, y, z)dv =
b
a
g2(x)
g1(x)
h2(x)
h1(x)
f(x, y, z)dz.dy.dx
Se tiene que:
h1(x, y) y h2(x, y) son los techos
El piso es la region D = {(x, y) ∈ R3
/ g1(x) ≤ y ≤ g2(x), a ≤ x ≤ b}
Figura 23:
Ejercicio Sea w la region limitada por los planos: x = 0, y = 0 z = 2 y la superfi-
cie z = x2
+ y2
y que esta en el cuadrante: x ≥ 0 y y ≥ 0
Calcular xdx.dy.dz y graficar la region.
La region w esta graficado luego podemos describir esta region mediante las desigualdades
0 ≤ x ≤
√
2, 0 ≤ y ≤
√
2 − x2, x2
+ y2
≤ z ≤ 2
30

31. Figura 24:
Por lo tanto
w
xdx.dy.dz =
√
2
0
√
2−x2
0
2
x2+y2 x.dz.dy.dx
=
√
2
0
√
2−x2
0
x [z]2
x2+y2 dy.dx = 8
√
2
15
4. COORDENADAS ESFERICAS
En un sistema de coordenadas esfericas se tiene:
Un plano polar y un eje Z perpendicular al plano polar con el origen del eje Z en el polo del
plano polar.
A las coordenadas esfericas de un punto del espacio denotaremos por P(ρ, θ, φ) en donde
ρ =
−→
OP > 0, θ es el angulo entre la direccion positiva del eje Z y el radio vector
−→
OP
Figura 25:
31

32. La relacion entre las coordenadas cartesianas y esfericas es:



x = ρ.cosθ.senφ
y = ρ.senθ.senφ
z = ρ.cosφ
ρ = OP , ρ > 0
r = OP
θ : angulo entre OX y OP , 0 ≤ θ ≤ 2π
φ : angulo entre OZ y OP, 0 ≤ φ ≤ π
x2
+ y2
+ z2
= r2
, tgθ = y
x
, φ = arccos z√
x2+y2+z2
Calculando en Jacobiano de las coordenadas esfericas se tiene
J(ρ, θ, φ) = ∂(x,y,z)
∂(ρ,θ,φ)
= det







∂x
∂ρ
∂x
∂θ
∂x
∂φ
∂y
∂ρ
∂y
∂θ
∂y
∂φ
∂z
∂ρ
∂z
∂θ
∂z
∂φ







=


cosθ.senθ − ρsenθ.senφ ρ.cosθ.cosφ
senθ.senφ ρ.cosθ.senφ ρ.senθ.cosφ
cosφ 0 − ρsenφ


J(ρ, θ, φ) = −r2
senφ
4.1. Integrales triples en coordenadas esfericas
Si una region Ω ⊂ R3
tiene un eje de simetria, las integrales triples tambien se pueden cal-
cular en forma muy simple, usando coordenadas esfericas y cuya relacion entre las coordenadas
cartesianas es:



x = ρ.cosθ.senφ
y = ρ.senθ.senφ
z = ρ.cosφ
Si f : Ω ⊂ R3
→ R es una funcion continua sobre Ω, entonces la transformacion de la in-
tegral triple Ω
f(x, y, z)dx.dy.dz en coordenadas esfericas es dado por:
Ω
f(x, y, z)dx.dy.dz = Ω
f(ρ.cosθ.senφ, ρ.senθ.senφ, ρ.cosφ) |J(ρ, θ, φ)| dρ.dθ.dφ
Cuando T(ρ.cosθ.cosφ, ρ.senθ.senφ, ρ.cosφ) = 1 se tiene el volumen del solido, es decir
V (S) = ρ2
.senφ.dρ.dφ.dθ
Un solido en coordenadas esfericas es un conjunto de la forma
Ω = {(ρ, θ, φ)/ Q1 ≤ ρ ≤ Q2, θ1 ≤ θ ≤ θ2, φ1 ≤ φ ≤ φ2}
De tal modo que el paralelepipedo rectangular en el espacio r, θ, φ
32

33. Ω = {(r, θ, φ)/ r1 ≤ r ≤ r2, θ1 ≤ θ ≤ θ2, φ1 ≤ φ ≤ φ2}
Es transformado por medio de la transformacion de coordenadas
T(r, θ, φ) = T(ρ.cosθ.cosφ, ρ.senθ.senφ, ρ.cosφ)
en un papalelepipedo esferico.
Ejercicio Evaluar la integral
2
0
√
4−y2
0
√
4−x2−y2
0
dz.dx.dy
x2+y2+z2 utilizando coordenadas es-
fericas.
Solucion



0 ≤ z ≤ 4 − x2 − y2
0 ≤ x ≤ 4 − y2
0 ≤ y ≤ 2
pasando a coordenadas esfericas
x = ρ.cosθ.senφ
y = ρ.senθ.senφ
z = ρ.cosφ
Ω = {(ρ, θ, φ)/ a1 ≤ ρ ≤ a2, θ1 ≤ θ ≤2, φ1 ≤ φ ≤ φ2}
Ω = (ρ, θ, φ)/ 0 ≤ ρ ≤ 2, 0 ≤ θ ≤ π
2
, 0 ≤ φ ≤ π
2
Jacobiano: J(ρ, θ, φ) = ρ2
senφ
2
0
√
4−y2
0
√
4−x2−y2
0
dz.dx.dy
x2+y2+z2 =
π
2
0
π
2
0
2
0
ρ2.senφ
ρ2 dρ dφ dθ
=
π
2
0
2dθ = π
5. COORDENADAS CILINDRICAS
Dado un punto P(x, y, z) ∈ R3
asociamos a el la terna (r, θ, z) donde (r, θ) son las coor-
denadas polares de la proyeccion P del punto P sobre el plano XY (es decir (r, θ) son las
coordenadas polares de punto P = (x, y, z) y z es la distancia dirigida del plano polar al punto
P
Decimos que los elementos de la terna (r, θ, z) son las coordenadas cilindricas del punto P.
Observese que en cierto sentido podemos decir que las coordenadas cilindricas son las coor-
denadas polares de R3
, donde la tercera coordenada que se encarga de medir la altura de un
punto al plano XY coincide con la del sistema rectangular.
La relacion entre las coordenadas cilindricas y rectangulares es:



x = r.cosθ, r ≥ 0
y = r.senθ, 0 ≤ θ ≤ 2π
z = z, z ∈ R
x2
+ y2
= r2
, tgθ = y
x
33

34. Figura 26:
Si e1, e0, ez son los vectores unitarios ortogonales que marcan la direccion donde se mide cada
una de los correspondientes coordenadas r, θ, z respectivamente en el sistema de coordenadas
cilindricas (por el cual e1, e0, ez constituye una base ortonormal de R3
) es claro que el vector
ez es justamente el vector k = (0, 0, 1) del sistema rectangular y que los vectores er, e0 son los
mismos que los vectores del sistema ortonormal de R2
Es decir, se tiene que
er = (cosθ, senθ, 0) = cosθi + senθj
eθ = (−senθ, cosθ, 0) = −senθi + cosθj
ez = k
El jacobiano de la transformacion T T = (r, θ, z) = (r.cosθ, r.senθ, z) es:
J(r, θ, z) = ∂(x,y,z)
∂(r,θ,z)
= det






∂x
∂r
∂x
∂θ
∂x
∂z
∂y
∂r
∂y
∂θ
∂y
∂z
∂z
∂r
∂z
∂θ
∂z
∂z






= det


cosθ − r.senθ 0
senθ r.cosθ 0
0 0 1

 = r
5.1. Integrales triples en coordenadas cilindricas
Si f : Ω ⊂ R3
→ R es una funcion continua sobre Ω, entonces la transformacion de la
integral triple. Ω
f(x, y, z)dx.dy.dz en coordenadas cilindricas es dado por
Ω
f(x, y, z)dx.dy.dz = Ω
f(r.cosθ, r.senθ, z) |J(r, θ, z)| dr.dθ.dz
Un solido en coordenadas cilindricas es un conjunto de la forma:
34

35. Ω = {(r, θ, z)/ r1 ≤ r ≤ r2, θ1 ≤ θ ≤ θ2, z1 ≤ z ≤ z2}
Los paralelepipedos rectangulares en el espacio r, θ, z del tipo
Ω = {(r, θ, z)/ r1 ≤ r ≤ r2, θ1 ≤ θ ≤ θ2, z1 ≤ z ≤ z2}
Se transforman inyectivamente por la funcion de tranformacion de coordenadas T(r, θ, z) =
(r.cosθ, r.senθ, z) en paralelepipedos cilindricos.
De modo que la formula de cambio de variables x, y, z a coordenadas cilindricas r, θ, z en
una integral triple se define como
Ω
f(x, y, z)dx.dy.dz = Ω
f(r.cosθ, r.senθ, z)r.dr.dθ.dz
Donde Ω es la region del espacio r, θ, z transformada en Ω por la funcion T
Ejercicio Calcular (x2
+y2
)dx.dy.dz donde el dominio esta limitado por las superficies
z = 1
2
(x2
+ y2
), z = 2
Solucion
Pasando a coordenadas cilindricas
x = r.cosθ
y = r.senθ
z = z
R = Ω
Ω = (r, θ, z)/ 0 ≤ r ≤ 2, 0 ≤ θ ≤ 2π, π2
2
≤ z ≤ 2
Ω
f(x, y, z)dx.dy.dz = Ω
(x2
+ y2
)dx.dy.dz
=
2
0
2π
0
2
r2
2
r2
.r.dz dθ dr = 16
3
π
6. CAMPOS ESCALARES Y VECTORIALES
6.1. Campo
Si se asigna a cada punto del espacio el valor de una funcion univoca del punto, se dice que
este espacio, como base o soporte de dicha magnitud es un campo.
Si la magnitud es escalar hablamos de un campo escalar.
Si la magnitud es vectorial hablamos de un campo vectorial.
En general tanto los campos escalares como los vectoriales son funcion del punto y tiempo.
Cuando los cambios no dependen del tiempo se dicen que son estaticos o estacionarios.
6.2. Campo Escalar
Definicion 1. Un campo escalar es una funcion real de varias variables en al que
a cada punto de su dominio se le asigna el valor que toma una determinada magnitud
35

36. escalar sobre dicho punto,
f : A ⊂ Rn
→ R
Definicion 2. Dado un campo escalar V (x, y, z), las superficies equiescalares o de ni-
vel son aquellas en las que el campo toma un valor determinadao. Responde a la ecuacion.
V (x, y, z, ) = K
Donde a la constante K se se suelen dar valores en progresion aritmetica: c, c + k, c + 2k,
etc (vease la figura 1) con el fin de representar graficamente el campo.
Figura 27:
Definicion 3. En matematicas y en fisica un campo escalar representa la distribu-
cion espacial de una magnitud escalar, asociando un valor a cada punto del espacio. En
matematicas el valor es un numero, en fisica es una magnitud fisica. Los campos escalares
se usan en fisica como por ejemplo para indicar la distribucion de la temperatura o la
presion de un gas en el espacio.
Como expresion matematica un campo escalar es una funcion de Rn
→ R esto quie-
re decir que se asocia cada punto de un espacio vectorial con un numero o escalar
f (x1, x2, x3, ..., xn). Esta funcion tambien es conocida como funcion de punto o funcion
escalar.
Ejemplos de campos escalares
Los que proporcionan la densidad
Los que proporcionan la temperatura
Los que proporcionan la altura, etc.
Ejemplos graficos de campos escalares
36

37. Figura 28:
Figura 29:
37

38. Ejemplo 1 Sea: f (x, y) = 100 − x2
− y2
obtener cuatro curvas de nivel.
Solucion Igualamos f(x, y) a una constante k
f(x, y) = k
100 − x2
− y2
= k
Si k = 0 → x2
+ y2
= 102
Si k = 75 → x2
+ y2
= 52
Si k = 19 → x2
+ y2
= 92
Si k = 51 → x2
+ y2
= 72
Se obtiene la siguiente grafica
Figura 30:
38

39. 6.3. Campo Vectorial
Definicion 1. Un campo vectorial en n dimensiones es una funcion F : D ⊂
Rn
→ Rn
que asigna a cada ‘punto P(x1, x2, x3, ..., xn) del conjunto D a un unico vector
F(P) = (F1(x1, ..., xn); ..., Fn(x1, ..., xn)) con cada punto inicial P.
Observaciones
i) Para el caso n = 2 (en el plano, vease la figura 5) el campo vectorial es representado por.
F(x, y) = (M(x, y), N(x, y))
Donde M y N son funciones reales de dos variables.
Figura 31:
ii) Para el caso n = 3 (en el espacio, vease figura 6) El campo vectorial es representado por
F (x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z))
Donde P, Q y R son funciones reales de tres variables.
Figura 32:
39

40. Ejemplo 2. Dibuje una muestra representativa de vectores del campo vectorial
F(x, y) = x√
x2+y2
, y√
x2+y2
= x√
x2+y2
i + y√
x2+y2
j
Solucion Para describir un campo vectorial F se considera un punto generico P(x, y)
del plano R2
y se define como el vector de posicion r =
−→
OP = xi + yj del punto P. Asi, F(x, y)
es un vector unitario en la direccion del vector posicion r (vease la figura 7)
Figura 33:
40

41. 7. INTEGRAL DE LINEA
7.1. Integral de linea
En esta seccion se generaliza el concepto de la integral simple
b
a
f(t)dt de una funcion f
definida en el intervalo [a, b] a una integral de uan funcion definida sobre una curva C. Esta
integral se llama integral de linea de f sobre dicha curva y se denota por c
f.
7.2. Integral de linea de primera especie
Definicion 1. Sea α : [a.b] → Rn
una curva regular tal que α ([a, b]) = C ⊂ Rn
es
su imagen de α
La integral de linea de primera especie de la funcion f a lo largo de la curva C con
respecto al parametro longitud de arco esta dada por.
c
f (x1, x2, ..., xn) ds =
b
a
f (α(t)) α (t) dt
=
b
a
f (α1(t), ...αn(t)) [α1]2
+ ... + [αn]2
dt
Con frecuencia, en lugar de integral de linea, tambien son usadas las expresiones integral
curvilinea e integral de contorno.
Observacion 1. Si f (x1, ..., xn) = 1, la integral de linea proporciona la longitud de
arco de la curva C, esto es,
L(C) =
c
1ds =
b
a
α dt =
b
a
[α1]2
+ ... + [αn]2
dt
Observacion 2. Sea α : [a, b] → R2
una curva regular tal que α ([a, b]) = C es su
imagen en R2
.
Sea f : D ⊂ R2
→ R una funcion continua y no negatica sobre el conjunto abierto D que
contiene a la curva C (vease la figura 8)
41

42. Figura 34:
Sea Pc una particion de la curva C comprendida desde P hasta Q en trozos, de modo que la lon-
gitud de cada uno de los elementos de la particion son respectivamente ∆s1, ∆s2, ..., ∆si, ..., ∆sn
Sea Pi(xi, yi, 0) un punto arbitrario en el trozo ∆si, tal que f(xi, yi) esta bien definida. Entonces
el area de la superficie lateral de la region comprendida entre la superficie z = f(x, y) y la curva
C es dada por
A(cortina) = l´ım
Pc →0
n
i=1
f(xi, yi)∆si =
c
f(x, y)ds
Por consiguiente, la integral de linea de la funcion f sobre la curva C desde P a Q es da-
da por
A(cortina) =
c
f(x, y)ds =
b
a
f [α(t)] α (t) dt
Ejemplo 3. Sea C una curva que da vuelta al rededor de la circunferencia x2
+ y2
= 1
en sentido contrario a las manecillas del reloj y sea f(x, y) = 1 + x.
Calcule c
f(x, y)ds.
Solucion La parametrizacion del circulo unitario C : x2
+ y2
= 1 esta dada por
C :
x = cost
y = sent
, 0 ≤ t 2π
Entonces α(t) = (cost, sent) y α(t) = (−sent, cost) por tanto la integral de linea de f sobre la
curva C es.
I =
c
f(x, y)ds =
2π
0
f(cost, sent) α(t) dt
=
2π
0
(1 + cost) (−sent)2 + cos2t dt =
2π
0
(1 + cost)dt = 2π
42

43. Ejemplo 4. Calcule c
xy2
z ds donde C es la interseccion de las superficies
x2
+ y2
+ z2
= 16 y x2
+ y2
= 4 en el primer octante.
Solucion La interseccion de las superficies x2
+ y2
+ z2
= 16 y x2
+ y2
= 4 en el
primer octante es la curva.
x2
+ y2
+ = 4 ∧ z = 2
√
3
Luego, la funcion vectorial que tiene como imagen a esta curva C es
α(t) = 2 cost, 2 sent, 2
√
3 t ∈ 0,
π
2
Figura 35:
Como α (t) = (−2 sent, 2 cos, 0) y α (t) = 2, entonces la integral de linea de al funcion
sobre la curva C resulta
c
xy2
z ds =
π
2
0
(2 cost)(2 sent)2
(2
√
3) α (t) dt
= 32
√
3
π
2
0
(sen2
t cost)dt =
32
√
3
3
PROPIEDADES DE LA INTEGRAL DE LINEA
1. Sea α : [a, b] → Rn
una curva regular, tal que α ([a, b]) = C ⊂ Rn
es su imagen
de α.
Sean f, g : D ⊂ Rn
→ R funciones definidas en el conjunto abierto D que contiene a la
curva C. Entonces se tiene:
a) c
kf(x1, ..., xn)ds = k c
f(x1, ..., xn)ds, siendo k una constante.
b) I = c
[f(x1, ..., xn) ± g(x1, ..., xn)] ds = c
f(x1, ..., xn)ds ± c
g(x1, ..., xn)ds
2. Si la curva C se forma uniendo los extremos de un numero finito de curvas re-
gulares C1, ..., Cn y C = C1 ∪ C2 ∪ ... ∪ Cn, entonces
43

44. I = c
f(x1, ..., xn)ds = c1
f(x1, ..., xn)ds + c2
f(x1, ..., xn)ds + ... cn
f(x1, ..., xn)ds
3. Dala la curva C con uan orientacion determianda, se denota por −C la misma
curva con una orientacion opuesta, y se verifica
−c
f(x1, ..., xn)ds = − c
f(x1, ..., xn)ds
4. C∪(−C)
f(x1, ..., xn)ds = C
f(x1, ..., xn)ds + −C
f(x1, ..., xn)ds = 0
Observacion 3. La masa de un cable de longitud L y de densidad δ : Rn
→ R esta
dado por
m =
C
δ(x1, ..., xn)ds
Donde C es el cble de longitud L
Observacion 4. La parametrizacion de una recta L ⊂ Rn
que tiene como punto ini-
cial A(a1, ..., an) y como punto final B(b1, ..., bn) esta dado por
α(t) = A + (B − A)t, t ∈ [0, 1]
Observacion 5. Cuando la integracion se realiza sobre una curva cerrada C, es cos-
tumbre denotar la integral de linea por f ds
7.3. Integral de linea de segunda especie
Definicion 2. Sea α : [a, b] → Rn
una curva seccionalmente regular, tal que
C = α ([a, b])
Sea F : D ⊂ Rn
→ Rn
un campo vectorial definido y acotado en la region D que
contiene a la curva C.
La integral de linea del campo vectorial F a lo largo de la curva C esta dado por:
C
F.dα =
b
a
F (α(t)) .α (t)dt
Observacion 6.
i) Si el campo vectorial F : D ⊂ R2
→ R2
es definida por F(x, y) = (M(x, y), N(x, y))
entonces al integral de linea de F a lo largo de la curva C ⊂ D esta dado por
44

45. I = C
[M(x, y)dx + N(x, y)dy] = C
F(α(t)).α (t)dt
=
b
a
[M(α1(t), α2(t))α1(t) + N(α1(t), α2(t))α2(t)] dt
ii) Si la curva regular C es α : [a, b] → R3
y el campo vectorial F : D ⊂ R3
→ R3
es
definida por
F(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z)), entonces la integral de linea de F a lo largo de C
esta dado por
I = C
[P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz] =
b
a
F(α(t)).α (t)dt
b
a
[P(α1(t), α2(t), α3(t))α1(t) + ... + R(α1(t), α2(t), α3(t))α3(t)] dt
Ejemplo 5. Evaluar la integral de linea C
[(3x − y)dx + (x + 2y)dy] donde C es la
imagen de la funcion vectorial α(t) = (cos t, sen t), t ∈ [0, 2π]
Solucion Como x = cos t y y = sen t, se tiene dx = −sen t dt y dy = cos t dt, por
tanto la integral de linea es
I = C
[(3x − y)dx + (x + 2y)dy]
2π
0
[(3 cost − sen t)(−sen t) + (cos t + 2 sent)(cos t)] dt = 2π
INDEPENDENCIA DE TRAYECTORIA EN INTEGRAL DE LINEA
Una integral de linea, en general, no depende solamente del integrando y de los puntos ini-
cial A y B, sino tambien de la curva de integracion que va desde el punto inicial A hasta el
punto final B.
Sin embargo, existe una clase muy importante de integrales de linea que son independientes de
la trayectoria de integracion. Esto ocurre cuando la forma diferencial que se pretende integrar
P(x, y, z) + Q(x, y, z)dy + R(x, y, z)dz es exacta, es decir, existe una funcion f : U ⊂ R3
→ R
tal que
df(x, y, z) = P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz
TEOREMA 1. Sea α : [a, b] → R3
una curva regular, tal que α([a, b]) = C;y sea F :
D ⊂ R3
→ R un campo vectorial continuo en la region D que contiene a la curva C, tal
que F(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z)), donde P, Q, R : D ⊂ R3
→ R3
son funciones
a valores reales con derivadas parciales continuas en a region D. Si al forma diferencial
P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz = F(x, y, z).dr(dr = (dx, dy, dz))
es exacta, entonces existe una funcion f : D ⊂ Rn
→ R, tal que
i) df(x, y, z) = P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz
ii) C
[P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz] depende solo de los extremos de a trayecto-
ria C que une los extremos
α(a) = A(x1, y1, z1).dr = f(x2, y2, z2) + f(x1, y1, z1) = f(B) − f(A)
45

46. Observacion 7.
a) Sean P, Q, R : D ⊂ R3
→ R funciones continuas con primeras derivadas parciales continuas
en la region D.
La forma diferencial P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz es exacta si y solo si
∂P
∂y
= ∂Q
∂x
, ∂P
∂z
= ∂R
∂x
, ∂Q
∂z
= ∂R
∂y
, ∀(x, y, z) ∈ D
b) Sean M, N : D ⊂ R2
→ R funciones continuas con derivadas parciales de primer orden
continuas en D. Entonces, la forma diferencial M(x, y)dx + N(x, y)dy es exacta si y solo si
∂M
∂y
= ∂N
∂x
, ∀(x, y) ∈ D
La aplicacion del teorema 1 a un campo vectorial definido en R2
se presenta en el siguien-
te corolario.
Corolario 1.- Sea α : [a.b] → R2
una curva regular tal que α([a, b]) = C y sea F : D ⊂
R2
→ R2
un campo vectorial continuo en la region D que contiene a la curva C tal que
F(x, y) = (M(c, y), N(x, y)), donde M, N : D ⊂ R2
→ R son funciones de clase C1
en la region
D.
Si la forma diferencial M(x, y)dx + N(x, y)dy = F(x, y).dr(dr = (dx, dy)) es exacta, enton-
ces existe una funcion f : D ⊂ R2
→ R, tal que
i) df(x, y) = M(x, y)dx + N(x, y)dy y
ii) C
[M(x, y)dx + N(x, y)dy] depende solamente de los extremos de la curva C : α(a) =
A(x1, y1) y α(b) = B(x2, y2) y se cumple
C
[M(x, y)dx + N(x, y)dy] = f(B) − f(A)
Observacion 8. Si la integral de una forma diferencial Pdx + Qdy + Rdz es independien-
te de la trayectoria de integracion, entonces la integral de esta forma diferencial sobre cualquier
curva cerrada es cero. Pues una curva cerrada C puede ser considerada como la union de dos
arcos C1 y C2, de modo que
C1
[Pdx + Qdy + Rdz] = C2
[Pdx + Qdy + Rdz]
Por tanto
C
[Pdx + Qdy + Rdz] = C1
+ C2
= C1
− −C2
= 0
En general se tiene el siguiente teorema:
TEOREMA 1. Sean P, Q, R : U ⊂ R3
→ R funciones continuas e U y sea C una curva
regular cerrada contenida en U con una representacion parametrica
α : [a, b] → R3
, tal que α ([a, b]) = C y α(a) = α(b).
La forma diferencial Pdx + Qdy + Rdz es exacta si y solo si
46

47. C
[Pdx + Qdy + Rdz] = 0
Ejemplo 6. Calcule C
(x + z, −y − z, x − y).dr, siendo C la curva de interseccion entre
la esfera x2
+ y2
+ z2
= 16 y el cilindro x2
+ y2
= 4x
Solucion Para el campo vectorial del integrando se tiene
P(x, y, z) = x + z, Q(x, y, z) = −y − z, R(x, y, z) = x − y
∂P
∂y
= 0 = ∂Q
∂x
, ∂P
∂z
= 1 = ∂R
∂x
, ∂Q
∂z
= −1 = ∂R
∂y
Como la forma diferencial P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz+ es exacta, entonces por
el teorema 2. la integral sobre la curva cerrada C es
C
(x + z, −y − z, x − y).dr = C
[(x + y)dx − (y + z)dy + (x − y)dz] = 0
47

48. 8. INTEGRAL DE SUPERFICIE
Sea E ⊂ R3
una superficie regular y g : E ⊂ R3
→ R una funcion definida sobre E, sea
φ : D ⊂ R2
→ R una parametrizacion propia de E, donde D es una region cerrada en R2
(vease
la figura 10)
Figura 36:
Sea P = {r1, r2, ..., rn} una particion de la region cerrada D ⊂ R2
, esta particion induce la
particion p = a1, a2, ..., an, de φ(D) donde σi = φ(ri) para i = 1, 2, ..., n
Sea (ui, vi) ∈ ri, un punto arbitrario tal que φ(ui, vi) = (xi, yi, zi). La suma de Riemann de
g correspondiente a la particion P es
n
i=1 g (xi, yi, zi) A(σi) = Area de σi
La integral de superficie de la funcion g sobre la superficie E esta dada por
I = E
d(x, y, z)dσ = l´ım A(σi) →0
n
i=1 g(xi, yi, zi)A(σi)
Observacion 9. Si E = φ(D), entonces la integral de superficie de g sobre E esta dada
por
I =
E
g(φ(u, v))
∂φ
∂u
×
∂φ
∂v
du.dv
Siempre que exista esta integral.
48

49. TEOREMA FUNDAMENTAL DE LA INTEGRAL DE SUPERFICIE
TEOREMA 1. Sea E una superficie regular de R3
, φ : D ⊂ R2
→ E una parametriza-
cion de E, tal que φ(u, v) = (φ1(u, v), φ2(u, v), φ3(u, v), )
Si g : E → R es funcion continua, entonces:
a) existe E
g(x, y, z)dσ
b) E
g(x, y, z)dσ = E
g (φ1(u, v), φ2(u, v), φ3(u, v)) φu × φv du.dv
Observacion 10. Sea D ⊂ R2
una region cerrada y f : D → R una funcion diferenciable
de clase C2
, su grafica es la superficie
E = Gf = (x, y, z) ∈ R3
/z = f(x, y), ∀(x, y) ∈ D
La parametrizacion de E es
φ : D → E ⊂ R3
definido por φ(x, y) = (x, y, f(x, y))
Sea g : E → R una funcion continua, entonces la integral de superficie de g sobre E esta dada
por
E
g(x, y, z)dσ =
E
g(x, y, f(x, y)) 1 +
∂f
∂x
2
+
∂f
∂y
2
dA
Ejemplo 7. Calcule E
g(x, y, z)dσ, donde g(x, y, z) = x2
z, E : z = 1 − x2 − y2
Solucion
Como z = f(x, y) = 1 − x2 − y2, fx = −x√
1−x2−y2
, fy = −y√
1−x2−y2
Entonces al aplicar la formula de la observacion 10, se tiene.
I = E
x2
z.dσ = E
1 − x2 − y2 1 + x2
1−x2−y2 + y2
1−x2−y2 dy.dx
Donde D = {(x, y) ∈ R2
/x2
+ y2
1} es la proyeccion de E sobre el plano XY por lo tan-
to.
I = D
x2
dy.dx =
1
−1
√
1−x2
−
√
1−x2 x2
dy.dx = 2
1
−1
x2
√
1 − x2dx = π
4
49

50. 9. LA DIVERGENCIA
Definicion 1. Definimos la divergencia de un campo vectorial F formalmente to-
mando el producto escalar del operador con F.
Divergencia: si F = F1i + F2j + F3k, la divergencia de F es el campo escalar
divF = F =
∂F1
∂x
+
∂F2
∂y
+
∂F3
∂z
Analogamente, si F = (F1, ..., Fn) es un campo vectorial en n
,su divergencia es
divF =
n
i→1
∂Fi
∂xi
=
∂F1
∂x1
+
∂F2
∂x2
+ ... +
∂Fn
∂xn
Ejemplo 1. Calcular la divergencia de: F = x2
yi + zj + xyzk
Solucion
div F =
∂(x2y)
∂x
+ ∂(z)
∂y
+ ∂(xyz)
∂z
= 2xy + 0 + xy
= 3xy
INTERPRETACION La divergencia tiene una importante interpretacion fi-
sica. Si imaginamos que F es en le campo de velocidades de un gas (o de un fluido),
entonces div F < 0 , el gas (o fluido)se esta comprimiendo. Para un campo vectorial en
el plano F(x, y) = F1i + F2j, la divergencia.
.F =
∂F1
∂x
+
∂F1
∂y
mide la razon de expansion del area. Esta interpretacion se explica graficamente del modo
siguiente. Tomemos una minima region W alrededor de un punto X0. Para cada punto x
de W tras un tiempo t.
50

51. Figura 37:
Denotamos la region resultante en el instante t por W(t) y sea v(t) su volumen (o area, si
estamos en dos dimensiones).entonces, la razon relativa de cambio de volumen es la divergencia,
mas exactamente,
1
ν(0)
d
dt
ν(t)|t=0 ≈ divF(x0)
donde la aproximacion se hace mas y mas segun W se contrae a x0. se puede encontrar una
prueba directa de este resultado en el suplemento de internet, pero este capitulo se representa
un argumento mas natural, en el contexto teoremas sobre integrales del calculo vectorial.
Ejemplo 1. considerar el campo vectorial en el plano dado por V(x,y) = xi. relacio-
nar el signo de la divergencia de V con la razon del cambio de areas bajo el flujo.
Solucion
interpretamos V como el campo de velocidades de un fluido en el plano. El campo vecto-
rial V apunta hacia la derecha para x > 0, y hacia la izquierda para x < 0, como podemos ver
el figura. la longitud de V es mas corta cuando nos acercamos al origen. cuando el fluido se
mueve, se expande (el area del rectangulo sombreado aumenta), de manera que es de esperar
que divV > 0. en efecto, div V = 1
Figura 38:
51

52. Ejemplo 2. las lineas de flujo del campo vectorial F = xi + yj son semi rectas que
parten del origen. Si estas lineas de flujo se corresponden con un fluido, entonces este se esta
expandiendo conforme se aleja del origen, de modo que div F deberia ser positiva. en efecto,
.F =
∂
∂x
x +
∂
∂y
y = 2 > 0
Figura 39:
Ejemplo 3. Consideramos el campo vectorial F = −xi − yj, a diferencia del caso ante-
rior, aqui las lineas de flujo apuntan hacia el origen. por tanto, el fluido se esta comprimiendo,
de manera que esperamos que div F < 0. Haciendo los calculos, vemos que
.F =
∂
∂x
(−x) +
∂
∂y
(−y) = −1 − 1 = −2 < 0
Figura 40:
Ejemplo 4. Como vimos en la ultima seccion, las lineas de flujo de F = −yi + xj son
circunferencias concentricas centradas en el origen, moviendose en sentido contrario a de las
agujas del reloj. segun la figura, parece que el fluido ni se comprime ni se expande. esto se
52

53. confirma calculando
.F =
∂
∂x
(−y) +
∂
∂y
(x) = 0 + 0 = 0
Figura 41:
Ejemplo 5. En la figura siguiente se muestra algunas lineas del flujo del campo F =
xi − yj. Aqui muestra intuicion sobre compresion o expansion no es tan clara; sin embargo, es
cierto que las regiones sombreadas tienen el mismo area, y calculamos que
.F =
∂
∂x
(x) +
∂
∂y
(−y) = 1 + (−1) = 0
Figura 42:
53

54. 10. ROTACIONAL
Para calcualar el rotacional,la segunda operacion basica para campos vectoriales, tomamos
formalmente el producto vectorial de con F.
El rotacional de un campo vectorial . Si F = F1i + F2j + F3k, entonces el rotacional de F en
el campo vectorial
rotF = × F =
i j k
∂
∂x
∂
∂y
∂
∂z
F1 F2 F3
=
∂F3
∂y
−
∂F2
∂z
i +
∂F1
∂z
−
∂F3
∂x
j +
∂F2
∂x
−
∂F1
∂y
k
Si usamos una notacion alternativa, y escribimos F = Pi + Qj + Rk, la formula del rota-
cional se escribe
rotF =
i j k
∂
∂x
∂
∂y
∂
∂z
P Q R
=
∂R
∂y
−
∂Q
∂z
i +
∂R
∂z
−
∂P
∂x
j +
∂Q
∂x
−
∂P
∂y
k
Ejemplo 1. sea F(x, y, z) = xi + xyj + k, hallar × F
Solucion
utilizamos la formula anterior:
× F =
i j k
∂
∂x
∂
∂y
∂
∂z
x xy 1
= (0 − 0)i − (0 − 0)j + (y − 0)k
por tanto, × F = yk
54

55. Ejemplo 2. hallar el rotacional del campo xyi − senzj + k
Solucion
sea F = xyi − senzj + k
× F =
i j k
∂
∂x
∂
∂y
∂
∂z
xy − sin z 1
=
∂
∂y
∂
∂z
− sin z 1
i −
∂
∂x
∂
∂z
xy 1
j +
∂
∂x
∂
∂y
xy − sin z
k
= cos zi − xk
A diferencia de la divergencia, que se puede definir en Rn
para cualquier n, solo definimos
el rotacional en un espacio tridimensional (o en caso de vectores en el plano, suponiendo que
su tercera componente es igual a cero).
10.1. El rotacional y las rotaciones
El significado fisico del rotacional sera discutido en el capitulo 7, cuando estudiemos el teore-
ma de stokes; sin embargo, podemos considerar una situacion especifica, en el cual el rotacional
esta asociado con rotaciones.
Ejemplo 1. Consideramos un solido rigido B que gira alrededor de un eje I. El mo-
vimiento de rotacion del cuerpo puede describirse mediante un vector ω a lo largo del eje de
rotacion, elijiendo su direccion de modo que el cuerpo gire en torno a ω, como en la figura.
Denominaremos al vector ω como vector velocidad angular del solido B, es decir, la rapidez
de cualquier punto de B dividida por su distancia al eje de rotacion L. El movimiento de los
puntos, en el cuerpo rotante esta descrito por el campo vectorial v cuyo valor en cada punto es
la velocidad en ese punto. para hallar v, sea Q un punto cualquiera en B, y sea α la distancia
entre Q y L.
55

56. Figura 43:
La figura muestra que α = r sin θ, donde r es el vector que parte del origen de coordenadas
y termina en Q, y θ es el angulo entre r y el eje de rotacion L. La velocidad tangencial v de Q
se dirigen en el sentido contrario a las agujas del reloj sobre la tangente a una circunferencia
paralela al plano XY de radio x, y tiene magnitud
v = ωα = ω r sin θ = r ω sin θ
la direccion y magnitud de v implican que v = ω × r. Eligiendo un sistema de coordena-
das en el cual L sea el eje z, podemos escribir ω = k y r = xi + yj + zk. Entonces,
v = ω × r = −ωyi + ωxj
y por tanto:
rotv =
i j k
∂
∂x
∂
∂y
∂
∂z
−ωy ωx 0
= 2ωk = 2ω
10.2. El rotacional y las rotaciones en flujo
Si un campo vectorial representa el flujo de un fluido, entonces el valor de ×F en un punto
es el doble de la velocidad angular de un reducido solido que rotase del mismo modo que lo
hace el fluido cerca de ese punto.En particular, ×F = 0 en un punto P significa que el fluido
esta libre de rotaciones rigidas en P, es decir, no tiene remolinos. Otra justificacion de esta
idea depende del teorema de Stokes del capitulo 7. Sin embargo, podemos decir informalmente
que rotF = 0 significa que si una diminuta rueda rigida dotada de paletas flota en el fluido, se
movera con el, pero no rotara alrededor de su eje. Tal campo se denomina irrotacional.
56

57. Por ejemplo, se ha determinado apartir de experimentos que el movimiento de un liquido con-
tenido en una cuba, mientras esta se vacia por un desague en su parte interior, es usualmente
irrotacional excepto justo en el centro, a pesar de que el fluido este girando alrededor del
desag¨ue. Las lineas de flujo del campo vectorial V son:
Figura 44:
Circunferencias centradas en el origen, a pesar de lo cual demostramos que el flujo es irrotacio-
nal; por tanto, el lector deberia estar prevenido ante la posible confusion que puede ocasionar
el termino irrotacional .
Ejemplo 2. Comprobar que el campo vectorial v(x, y, z) = yi−xj
x2+y2 es irrotacional (x, y) =
(0, 0) (es decir, exepto cuando v no esta definido).
Solucion
× v =
i j k
∂
∂x
∂
∂y
∂
∂z
y
x2+y2
−x
x2+y2 0
= 0i + 0j +
∂
∂x
−x
x2 + y2
−
∂
∂y
y
x2 + y2
k
=
− (x2
+ y2
) + 2x2
(x2 + y2)2 +
− (x2
+ y2
) + 2y2
(x2 + y2)2 k = 0
10.3. Los campos gradientes son irrotacionales
La siguiente identidad es un relacion basica entre gradiente y rotacional, que se deberia
comparar con el hecho de que para cualquier v se tiene v × v = 0.
57

58. TEOREMA 1. El rotacional de un gradiente
Sea f una funcion C2
.Entonces:
× ( ) = 0
Es decir, el rotacional de cualquier gradiente es el vector cero.
Ejemplo 3. Sea V (x, y, z) = yi − xj. Demostrar que V no es campo gradiente.
Solucion
Si V fuera un campo gradiente, segun el teorema 1 deberia verificar rotV = 0. Pero:
rotvV =
i j k
∂
∂x
∂
∂y
∂
∂z
y −x 0
= −2k = 0
De manera que V no puede ser un gradiente.
10.4. Rotacional escalar
Hay una operacion sobre campos vectoriales en el plano que esta muy relacionado con el
concepto de rotacional. Si F(x, y) = P(x, y)i + Q(x, y)j es un campo vectorial en el plano,
tambien puede interpretarse como un campo vectorial en el espacio tridimensional, para lo cual
el componente k es igual a cero y las otras dos coordenadas son idependientes de la coordenada
z. Entonces el rotacional de F se reduce a:
× F =
∂Q
∂x
−
∂P
∂y
k
Y siempre apunta en la direccion k la funcion:
∂Q
∂x
−
∂P
∂y
que depende de las variables x y y y se denomina el rotacional escalar de F
Ejemplo 4. Hallar el rotacional escalar de V (x, y) = y2
i + xj
Solucion
El rotacional es:
58

59. × V =
i j k
∂
∂x
∂
∂y
∂
∂z
y2
x 0
= (1 + 2y)k
de modo que el rotacional escalar, que es el coeficiente de k, vale 1 + 2y.
10.5. Las rotaciones tienen divergenncia cero
A continuacion, enunciamos una relacion basica entre los operadores divergencia y rotacio-
nal.
TEOREMA 2. La divergencia de un rotacional
Para cualquier campo vectorial F de clase C2
div rot F = . ( × F) = 0
Es decir, la divergencia de cualquier rotacional es cero.
Al igual que ocurria en la prueba de que el rotacional de un gradiente es cero, en este caso la
demostracion del teorema se basa en la igualdad de las derivadas cruzadas.
Ejemplo 5. Demostrar que el campo vectorial V (x, y, z) = −xi + yj + zk no puede ser
el rotacional de ningun campo vectorial F; es decir, no existe ningun campo F talque V = rotF.
Solucion
Si existiera un tal F, segun el teorema 2 deberiamos tener divV = 0. Pero:
div V =
∂x
∂x
+
∂y
∂y
+
∂z
∂z
= 3 = 0
de modo que V no puede ser rotF para ningun F.
11. EL LAPLACIANO
El operador de laplace 2
, que actua sobre funciones f, se define como la divergencia del
gradiente:
2
f = . ( f) =
∂2
f
∂x2
+
∂2
f
∂y2
+
∂2
f
∂z2
59

60. Este operador ejerce un importante papel en muchas leyes fisicas,como ya mencionaron en
capitulos anteriores.
Ejemplo 1. Demostrar que 2
f = 0 para
f(x, y, z) =
1
x2 + y2 + z2
=
1
r
y
(x, y, z) = 0
donde r = xi + yj + zk y r = r
Solucion
Las primeras derivadas son:
∂f
∂x
=
−x
(x2 + y2 + z2)3/2
∂f
∂y
=
−y
(x2 + y2 + z2)3/2
∂f
∂z
=
−z
(x2 + y2 + z2)3/2
calculando las derivadas segundas, resulta:
∂2
f
∂x2
=
3x2
(x2 + y2 + z2)5/2
−
1
(x2 + y2 + z2)3/2
∂2
f
∂y2
=
3y2
(x2 + y2 + z2)5/2
−
1
(x2 + y2 + z2)3/2
∂2
f
∂z2
=
3z2
(x2 + y2 + z2)5/2
−
1
(x2 + y2 + z2)3/2
por tanto,
∂2
f
∂x2
+
∂2
f
∂y2
+
∂2
f
∂z2
=
3(x2
+ y2
+ z2
)
(x2 + y2 + z2)5/2
−
3
(x2 + y2 + z2)3/2
60

61. =
3
(x2 + y2 + z2)3/2
−
3
(x2 + y2 + z2)3/2
= 0
11.1. Identidades vectoriales
En este momento tenemos a nuestra disposicion cuatro operadores basicos: gradiente, di-
vergencia, rotacional y laplaciano. La siguiente lista contiene algunas formulas que son utiles
cuando se calcula con campos vectoriales.
Identidades basicas del analisis vectorial
a) (f + g) = f + g
b) (cf) = c f, para cualquier constante c
c) (fg) = f g + g f
d) (f/g) = (g f − f g)/g2
, en aquellos puntos x en los que g(x) = 0
e) div(F + G) = divF + divG
f) rot(F + G) = rotF + rotG
g) div(fF) = fdivF + f
h) div(F × G) = G.rotF − F.rotG
i) divrotF = 0
j) rot(fF) = frotF + f × F
k) rot f = 0
l) 2
(fg) = f 2
g + g 2
f + 2( f. g)
m) div( f × g) = 0
n) div(f g − g f) = f 2
g − g 2
f
61

62. 12. TEOREMA DE GREEN
Existe una relacion muy importante entre las integrales dobles y las integrales de linea que a
continuacion se presenta. Esto concierne a las integrales de linea sobre curvas cerradas simples.
Antes de introducir este importante teorema , introducimos algunas definiciones preliminares.
Definicion 1. Una curva cerrada regular α : [a, b] → R2
es simple, si α es una
funcion uno a uno, excepto en los extremos del intervalo donde α(a) = α(b)
Definicion 2. Una region S ⊂ R2
es simplemente conexo, si toda la curva cerrada
simple α de S se puede deformar continuamente a un punto sin salirse de S (vease la
figura 11)
Figura 45: 0.7
Teorema de Green.- Sea V ⊂ R2
una region abierta, S ⊂ V una region cerrada
simplemente conexa cuya frontera FrS = C ⊂ R2
es una curva cerrada regular simple.
Si M, N, ∂M
∂y
, ∂N
∂x
: V ⊂ R2
→ R son funciones continuas sobre S, entonces
FrS
[M(x, y)dx + N(x, y)dy] =
S
∂N
∂x
−
∂M
∂y
dA
Observacion 1. Si ∂N
∂x
−∂M
∂y
= 1, entonces el area de la region S es A(S) = FrS
[Mdx + Ndy]
62

63. Teorema (integral de linea para el calculo del area de una region). Si D ⊂ R2
es
una region limitada por un camino cerrado C. Entonces el area de la region D esta dada
por
A(D) = 1
2 C
[xdy − ydx]
Ejemplo 1. Sea D la region interior al rectangulo de vertices (7, 4), (−7, 4), (−7, −4)y(7, −4)
y exterior al cuadrado de vertices (2, 2), (−2, 2), (−2, −2), (2, −2). Al denotar con C a la
frontera de esta region. Calcule la integral de linea
C
4xydx + (2x2
+ 4x)dy
Solucion
Como M = 4xy y N = 2x2
+ 4x, se tiene
∂N
∂x
= 4x + 4 y ∂M
∂y
= 4x
Al aplicar el teorema de Green a lo largo de la trayectoria C = C1 ∪ C2 ∪ C3 ∪ C4,
como se muestra en la figura 12, se tiene
I = C
[4xydx + (2x2
+ 4x)dy] = D
∂N
∂x
− ∂M
∂y
dA = D
(4x + 4 − 4x) dA
4 D
4(area de D) = 4(area del rectangulo − area del cuadrado)
= 4(112 − 16) = 338
Figura 46:
63

64. Observacion 2. El teorema de Green puede extenderse a conjuntos mas generales de
manera sencilla. Supongamos que el conjunto S tiene como frontera dos curvas cerradas
simples α1 y α2 que recorren en sentido contrario a las manecillas del reloj con relacion
a S. Esto significa que la region S siempre esta a la izquierda cuando una particula se
mueve sobre α1 o α2 (vease la figura 13)
Figura 47:
Conectamos α1 y α2 mediante dos rectas que no se intersecan o mediante trayectorias
poligonales como se muestra en la figura 14. Ahora el conjunto S esta dividido en dos
conjuntos S1 y 2 cada uno de las cuales tiene una curva frontera cerrada simple γ1 y γ2,
respectivamente. Entonces segun el teorema de Green, se tiene.
γ1
(Mdx + Ndy) = s1
∂N
∂x
− ∂M
∂y
dA, i = 1, 2, ... Luego.
S
∂N
∂x
− ∂M
∂y
dA = α1
(Mdx + Ndy) + α2
(Mdx + Ndy)
= γ1
(Mdx + Ndy) + γ2
(Mdx + Ndy)
Teorema 2 Sea S un conjunto cerrado y acotado de R2
, tal que la frontera se reco-
rre por un numero finito de curvas cerradas imples α1, α2, ..., αn.
Supongamos que cada curva αk esta orientada positivamente con respecto a S.
Si M, N : S ⊂ R2
son funciones continuas en una vecindad de S, entonces
S
∂N
∂x
−
∂M
∂y
dA =
k=1 ak
(Mdx + Ndy)
64

65. Ejemplo 1. Sea S la region exterior al circulo unitario C2 que esta limitada por la
izquierda por la parabola y2
= 4(4 + x) y por la derecha por la recta x = 4 (vease la figura 15)
utilizando el teorema de Green, calcule.
C1
− y
x2+y2 dx + x
2+y2 dy
Donde C1 es la frontera exterior de S orientada como se muestra en la figura 15.
Solucion
Como M = − y
x2+y2 y N = x
x2+y2 , se tiene
∂M
∂y
= − x2−y2
(x2+y2)2 y ∂N
∂x
= x
(x2+y2)2
Asi por el teorema de Green se tiene
C1+C2
− y
x2+y2 dx + x
x2+y2 = S
∂N
∂x
− ∂M
∂y
dA = S
0dA = 0
Luego.
C1
− y
x2+y2 dx + x
x2+y2 dy = − C2
− y
x2+y2 dx + x
x2+y2 dy
El cual es equivalente a
C1
− y
x2+y2 dx + x
x2+y2 dy = −C2
− y
x2+y2 dx + x
x2+y2 dy
Esto indica que la curva −C2 esta orentada en sentido antihorario, esto es, la funcion vec-
torial que representa a esta curva es −C2 : α(t) = (cost, sent), t ∈ [0, 2π], por lo tanto la
integral de linea es
C1
− y
x2+y2 dx + x
x2+y2 dy =
2π
0
[sen2
t + cos2
t] dt = 2π
65

66. 13. TEOREMA DE STOKES
Podemos considerar que el teorema de Stokes es una version para varias dimensiones del
teorema de Green. Mientras el teorema de Green relaciona una integral doble sobre una region
D plana con una integral de linea alrededor de su curva frontera plana, el teorema de Stokes
relaciona una integral de superficie S con una integral de linea al rededor de la curva frontera
de S (que es una curva en el espacio). En la figura 14 se muestra una superficie orientada con
vector normal unitario n. La orientacion de S induce la orientacion positiva de la curva frontera
C ilustrada en la figura. Esto significa que si usted camina en la direccion positiva al rededor
de C con su cabeza en la direccion de n, entonces la superficie siempre quedara a su izquierda.
Figura 48:
Teorema de Stokes
Sea S uan superficie suave por tramos, simple y cerrada con orientacion positiva. Sea F un
campo vectorial cuyas componentes tienen derivadas parciales continuas en una region abierta
en R3
que contiene a S. Entonces
C
F.dr =
S
rot F.dS
Puesto que
C
Fdr = C
F.Tds y S
rot F.dS = S
rot F.ndS
El teorema de Stokes establece que la integral de linea al rededor de la curva frontera S de la
componente tangencial de F es igual a la integral de superficie de la componente normal del
rotacional de F.
La curva acotada orientada en forma positiva de la superficie orientada S se escribe a menudo
como ∂S, de modo que el teorema de Stokes se puede expresar como
S
rot F.ds =
∂x
F.dr ....ecuacion 1
66

67. Una analogia entre el teorema de Stokes, el eorema de Green y el teorema del calculo. Co-
mo antes hay una integral con derivadas en el primer miembro de la ecuacion 1 (recuerde que
rot F es una clase de derivada de F) y el segundo miembro contiene los valores de F solo sobre
la frontera de S.
De hecho, en el caso especial donde la superficie S es plana y queda en el plano XY con orienta-
cion hacia arriba, la Normal unitaria es k, la integral de superficie se vuelve una integral doble,
y el teorema de Stokes se transforma en
C
F.dx =
S
rot F.dS =
S
(rot F).k dA
Esto es precisamente la forma vectorial del teorema de Green, po tanto, el teorema de Green
es un caso especial del teorema de Stokes.
Ejemplo 1. Evalue C
F.dr donde F(x, y, z) = −y2 ¯i + x¯j + z2¯k y C es la curva de
la interseccion del plano y +z = 2 y el cilindro x2
+y2
= 1. (la orientacion de C es en el sentido
contrario al de las manecillas del reloj cuando se le ve desde arriba).
Solucion
La curva C (una elipse) se ilustra en la figura 15. aunque C
F.dr se puede evaluar en for-
ma directa, es mas facil aplicar el teorema de Stokes. Primero calculamos.
rot F =
i j k
∂
∂x
∂
∂y
∂
∂z
−y2
x z
= (1 + 2y)k
Figura 49:
67

68. Aunque hay muchas superficies cuya frontera es C, la eleccion mas conveniente es la region
eliptica S en el plano y+z = 2 que esta acotada por C. Si orientamos a S hacia arriba, entonces
C tiene la orientacion positiva inducida. La proyeccion D de S sobre el plano XY es el disco
x2
+ y2
≤ 1, por lo que al aplicar la ecuacion 1 con z = g(x, y) = 2 − y tenemos
C
F.dr =
S
rot F.dS =
D
(1 + 2y)dA
=
2π
0
1
0
(1 + 2rsenθ)rdr.dθ
=
2π
0
r2
2
+ 2
r3
3
senθ
1
0
dθ =
2π
0
1
2
+
2
3
senθ dθ
=
1
2
(2π) + 0 = π
68

69. 14. REFERENCIAS BIBLIOGRAFICAS
Stewart J. (2006) Calculo. Mexico, D.F: Progreso, S.A. de C.V.
Mitacc M.(2011) Calculo III. Lima, THALES
Lazaro M. (2010) Analisis matematico III. Lima, MOSHERA
Pita R. (1995) Calculo vectorial. Mexico, D.F, PROGRAMAS EDUCATIVOS S.A.
Marsden E. (1991) Calculo vectorial. Mexico, D.F. Freeman and company
Piskunov N. (1977) Calculo diferencial e integral. Moscu, Mir moscu
Espinoza R. (2000) Analisis matematico III. Lina, Eduardo Espinoza Ramos
Sitios web
http://www.esi2.us.es/DFA/CEMI/Teoria/Tema1.pdf
http://caminos.udc.es/info/asignaturas/obras-publicas/203/pdfs/Int-dobles-imp.pdf
http://www.ehu.eus/-mtpalezp/libros/05-4.pdf
http://caminos.udc.es/info/asignaturas/obras-publicas/203/pdfs/Int-dobles-imp.pdf
http://rua.ua.es/dspace/bitstream/10045/11355/3/Campos-esc-y-vect.pdf
http://es.slideshare.net/organico9825/coordenadas-cilindricas-y-esfricas
http://www.ehu.eus/-mtpalezp/libros/06-5.pdf
http://www.ugr.es/-rpaya/documentos/Teleco/Fund-Mat02.pdf
69