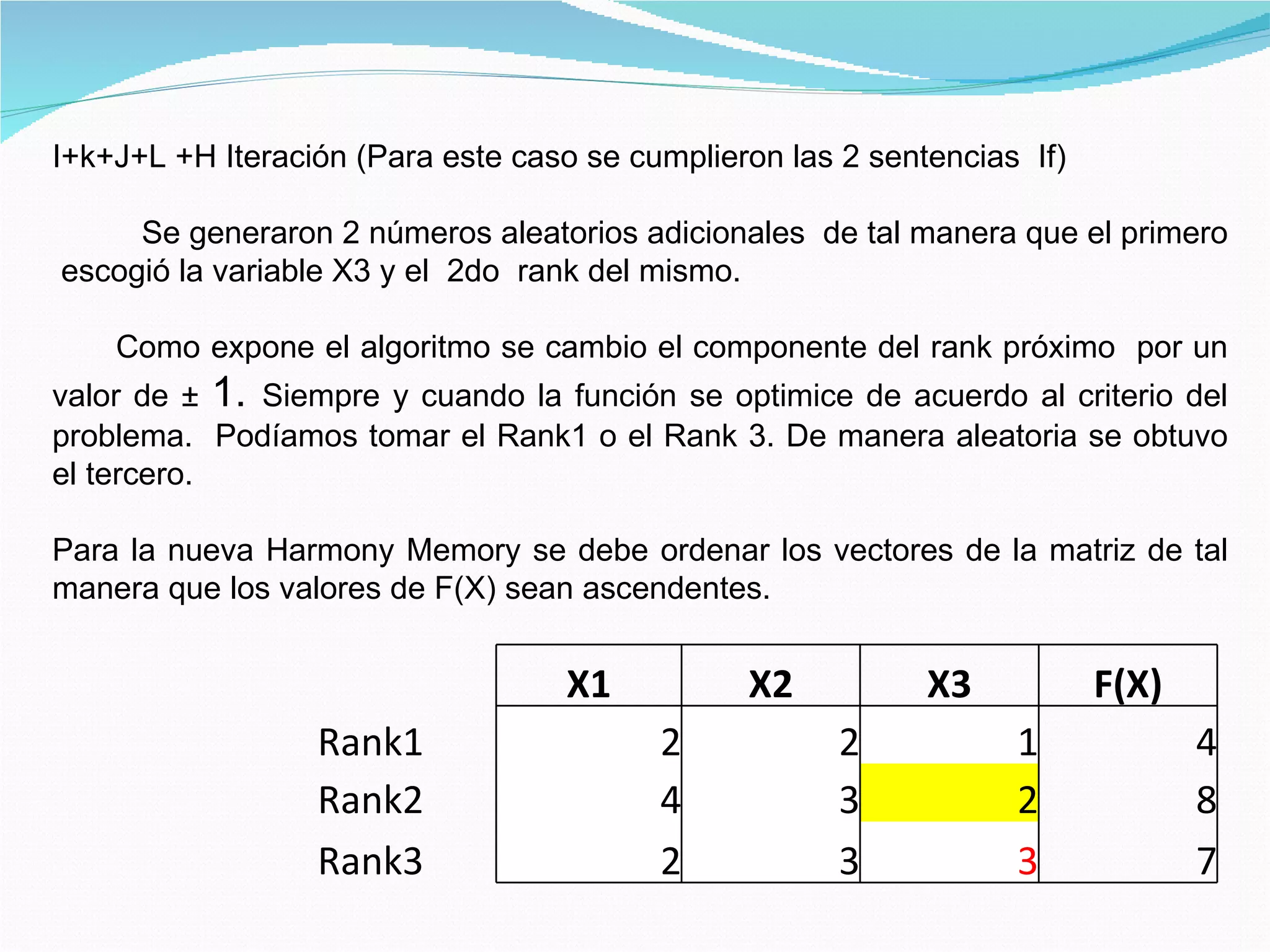
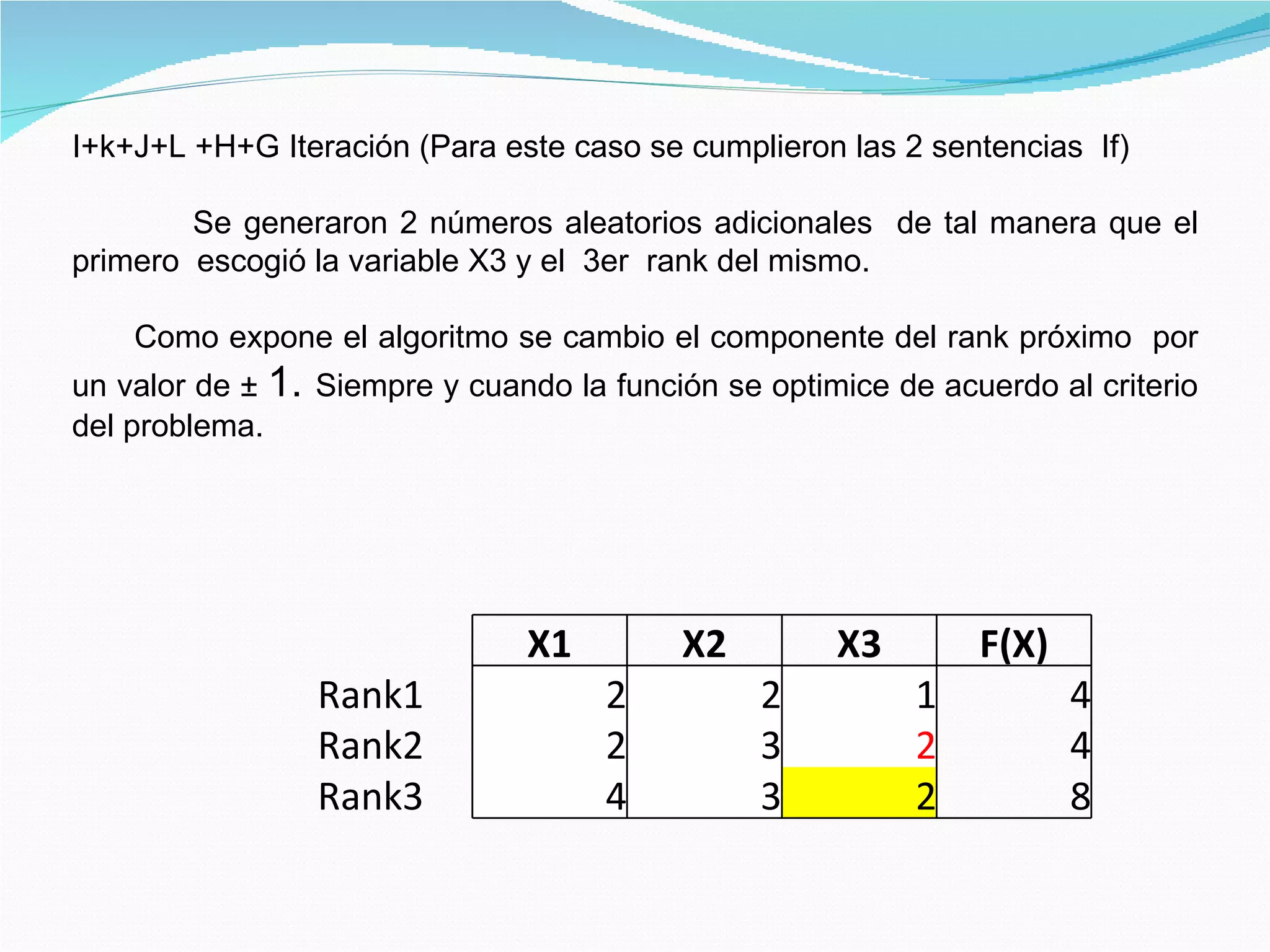
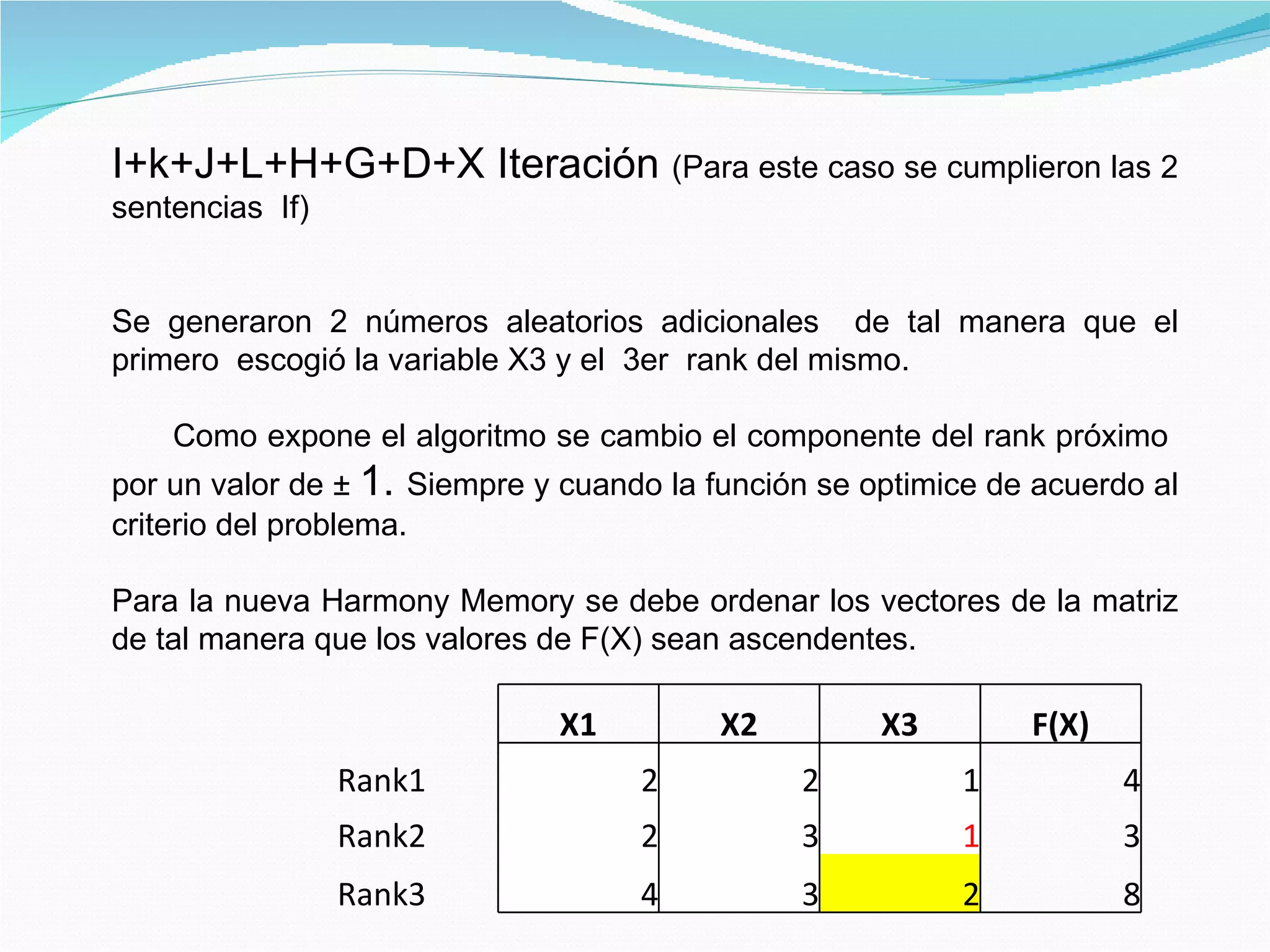
El documento describe el algoritmo de búsqueda de armonía, un algoritmo metaheurístico inspirado en el proceso de improvisación musical. Explica los parámetros de inicialización, la memoria de armonía, la generación de nuevas armonías a través de la selección aleatoria y el ajuste de tono, y la actualización de la memoria de armonía. También presenta un ejemplo de aplicación del algoritmo para optimizar una función objetivo.

1. Marcelo Apolo E.
César Menéndez C.
Nelson Ruíz
William Sánchez V.

2. HARMONY SEARCH
Es un algoritmo meta heurístico (también conocido
como algoritmo de cálculo suave o algoritmo
evolutivo), el cual imita el proceso de improvisación
musical.

3. HARMONY SEARCH
 La m ú s ic a (del griego: μουσική [τέχνη] - mousikē
[téchnē], "el arte de las musas") es, según la
definición tradicional del término, el arte de organizar
sensible y lógicamente una combinación coherente
de sonidos y silencios utilizando los principios
fundamentales de la melodía, la armonía y el ritmo,
mediante la intervención de complejos procesos
psico-anímicos.

4. Elementos de la música
 La organización coherente de los sonidos y los silencios
(según una forma de percepción) nos da los parámetros
fundamentales de la música, que son la melodía, la
armonía y el ritmo.
 La melodía es un conjunto de sonidos.
 La armonía, bajo una concepción vertical de la
sonoridad, y cuya unidad básica es el acorde, regula la
concordancia entre sonidos que suenan
simultáneamente y su enlace con sonidos vecinos.
 La métrica, se refiere a la pauta de repetición a intervalos
regulares, y en ciertas ocasiones irregulares, de sonidos
fuertes o débiles y silencios en una composición.
 El ritmo, es el resultado final de los elementos anteriores,
a veces con variaciones muy notorias.

5. FACTORES DE COMPARACION
 Conjunto de Músicos → Variables de Decisión
 Rango de Afinación→ Rango de Valores
 Armonía → Solución de vectores
 Estética → Función Objetivo
 Práctica → Iteración
 Experiencia → Matriz de memoria

6. Procedimientos de Harmony
Search
2. Parámetros de inicialización
3. Harmony Memory
4. Nueva Armonía
5. Actualización de Harmony Memory
6. Criterio de Verificación y Terminación

7. Parámetros de Inicialización
Minimizar o Maximizar F(X)
Sujeto
; i=1,2, … ,N
 N es el número de variables de decisión
 K es el número de candidatos de las variables de
decisión.

8. HARMONY MEMORY INICIAL
k

9. Nueva Armonía “Vector Harmony”
El nuevo vector Harmony x´ =
Dicho vector esta dado por tres reglas:
a Selección Aleatoria
r Se debe considerar HM
a Se debe hacer un ajuste (Ajuste de Tono)

10. Vector Harmony
SELECCIÓN ALEATORIA
Partimos de que el músico puede entonar cualquier
nota del pentagrama y que tiene grabada la melodía
en su memoria (HM).

11. Vector Harmony
SELECCIÓN ALEATORIA
Donde

12. Ajuste de Tono
 Una vez que obtuvimos el nuevo tono (Vector Harmony),
el músico puede ajustar aún mas el paso, probando con
notas vecinas.
Ejemplo: Sol su vecindad es La o Fa
En este caso Do puede ajustar a Re

13. Ajuste de Tono
Donde se obtiene del HM y es el K-ésimo
elemento de .
m es el índice de la vecindad ;
Para variables discretas m varía entre 1 y -1

14. Actualización de Harmony Memory
Si x´ = tie ne una me jor
re s pue s ta e n la función ob je tivo, lo
re e mplazamos e n la Harmony Me mory.

15. Presentación del Algoritmo
Harmony Search
Defina Función Objetivo F(x)
Defina Harmony Memory (Raccept)
Defina Ajuste de Tono (Rap)
Generar Harmony Memory con armonías aleatorias
While (t <Maximo_Numero_Iteraciones)
While (i <=Numero_Variables)
If (U [0,1 ] <Raccept)
Elegir un valor del Harmony Memory por la variable i
If (U [0,1] <Rap)
Ajustar el valor mediante la adición de cierta cantidad
End If
Else
Elegir un valor aleatorio
End If
End While
Aceptar el new Harmony si es mejor
End While
Buscar la actual mejor solución

16. Aplicaciones y Comparaciones con
otros Modelos
 Diseño de Estructuras

17. Aplicaciones y Comparaciones con
otros Modelos
 Problemas de Logística de Transportes

18. Aplicaciones y Comparaciones con
otros Modelos
 Diseño de Redes de Aguas

19. Aplicaciones y Comparaciones con
otros Modelos
 Diseño de Redes de Aguas en Gran Escala

20. Aplicaciones y Comparaciones con
otros Modelos
 Operaciones de Represas

21. Aplicaciones y Comparaciones con
otros Modelos
 Optimizar parámetros de Calibración Hidrológicas

22. Aplicaciones y Comparaciones con
otros Modelos
 Conservación Ecológica

23. Conclusiones
 El HS no requiere de cálculos complejos, por lo
tanto siempre esta libre de divergencia.
 El HS no requiere ajustes de valor inicial para las
variables de decisión.
 El HS puede manejar variables discretas, así como
variables continuas, mientras que las técnicas
basadas en gradiente solo pueden manejar
continuas.

24. EJERCICIO DE APLICACION
OBS:

25. PASO 1
Generar una Harmony Memory
X1 X2 X3 F(X)
2 2 1 4
1 3 4 13
5 3 3 16

26. PASO 2 “Recordar Bucles y Sentencias de Decisión”
Seguir los pasos del algoritmo, lo volvemos a anunciar
While (t <Maximo_Numero_Iteraciones)
While (i <=Numero_Variables)
If (U [0,1 ] <Raccept)
Elegir un valor del Harmony Memory por la variable i
If (U [0,1] <Rap)
Ajustar el valor mediante la adición de cierta cantidad
End If
Else
Elegir un valor aleatorio
End If
End While
Aceptar el new Harmony si es mejor

27. PASO 3
I-ésima Iteración (Para este caso se cumplieron las 2 sentencias If)
Se generaron 2 números aleatorios adicionales de tal manera que el
primero escogió la variable X1 y el 3er rank del mismo.
Como expone el algoritmo se cambio el componente del rank próximo
por un valor de ± 1. Siempre y cuando la función se optimice de acuerdo al
criterio del problema. X1 X2 X3 F(X)
Rank1 2 2 1 4
Rank2 2 3 4 12
Rank3 5 3 3 16

28. I+K Iteración (Para este caso se cumplieron las 2 sentencias If)
Se generaron 2 números aleatorios adicionales de tal manera
que el primero escogió la variable X2 y el 3er rank del mismo.
Como expone el algoritmo se debería cambiar el componente del
Rank próximo por un valor de ± 1. Pero en este caso la función
objetivo no optimiza por lo que no escogemos el vector Harmony en la
Harmony Memory.
X1 X2 X3 F(X)
Rank1 2 2 1 4
Rank2 2 3 4 12
Rank3 5 3 3 16

29. I+k+J Iteración (Para este caso se cumplieron las 2 sentencias If)
Se generaron 2 números aleatorios adicionales de tal manera que el
primero escogió la variable X3 y el 2do rank del mismo.
Como expone el algoritmo se cambio el componente del rank próximo
por un valor de ± 1. Siempre y cuando la función se optimice de acuerdo al
criterio del problema. Podíamos tomar el rank1 o el Rank 3. De manera
aleatoria se obtuvo el tercero.
X1 X2 X3 F(X)
Rank1 2 2 1 4
Rank2 2 3 4 12
Rank3 5 3 2 13

30. I+k+J+L Iteración (Para este caso se cumplieron las 2 sentencias If)
Se generaron 2 números aleatorios adicionales de tal manera que el
primero escogió la variable X1 y el 2do rank del mismo.
Como expone el algoritmo se cambio el componente del rank próximo por
un valor de ± 1. Siempre y cuando la función se optimice de acuerdo al criterio
del problema. Podíamos tomar el Rank1 o el Rank 3. De manera aleatoria se
obtuvo el tercero.
Para la nueva Harmony Memory se debe ordenar los vectores de la matriz de tal
manera que los valores de F(X) sean ascendentes.
X1 X2 X3 F(X)
Rank1 2 2 1 4
Rank2 2 3 4 12
rank3 4 3 2 8

31. I+k+J+L +H Iteración (Para este caso se cumplieron las 2 sentencias If)
Se generaron 2 números aleatorios adicionales de tal manera que el primero
escogió la variable X3 y el 2do rank del mismo.
Como expone el algoritmo se cambio el componente del rank próximo por un
valor de ± 1. Siempre y cuando la función se optimice de acuerdo al criterio del
problema. Podíamos tomar el Rank1 o el Rank 3. De manera aleatoria se obtuvo
el tercero.
Para la nueva Harmony Memory se debe ordenar los vectores de la matriz de tal
manera que los valores de F(X) sean ascendentes.
X1 X2 X3 F(X)
Rank1 2 2 1 4
Rank2 4 3 2 8
Rank3 2 3 3 7

32. I+k+J+L +H+G Iteración (Para este caso se cumplieron las 2 sentencias If)
Se generaron 2 números aleatorios adicionales de tal manera que el
primero escogió la variable X3 y el 3er rank del mismo.
Como expone el algoritmo se cambio el componente del rank próximo por
un valor de ± 1. Siempre y cuando la función se optimice de acuerdo al criterio
del problema.
X1 X2 X3 F(X)
Rank1 2 2 1 4
Rank2 2 3 2 4
Rank3 4 3 2 8

33. I+k+J+L+H+G+D Iteración (Para este caso se cumplieron las 2
sentencias If)
Se generaron 2 números aleatorios adicionales de tal manera que el
primero escogió la variable X2 y el 3er rank del mismo.
Como expone el algoritmo se debería cambiar el componente del Rank
próximo por un valor de ± 1. Pero en este caso la función objetivo no optimiza
por lo que no escogemos el vector Harmony en la Harmony Memory.
X1 X2 X3 F(X)
Rank1 2 2 1 4
Rank2 2 3 2 4
Rank3 4 3 2 8

34. I+k+J+L+H+G+D+X Iteración (Para este caso se cumplieron las 2
sentencias If)
Se generaron 2 números aleatorios adicionales de tal manera que el
primero escogió la variable X3 y el 3er rank del mismo.
Como expone el algoritmo se cambio el componente del rank próximo
por un valor de ± 1. Siempre y cuando la función se optimice de acuerdo al
criterio del problema.
Para la nueva Harmony Memory se debe ordenar los vectores de la matriz
de tal manera que los valores de F(X) sean ascendentes.
X1 X2 X3 F(X)
Rank1 2 2 1 4
Rank2 2 3 1 3
Rank3 4 3 2 8

35. Solución Óptima
Rank 1= (2,3,1)
F(X)=3
X1 X2 X3 F(X)
Rank1 2 3 1 3
Rank2 2 2 1 4
Rank3 4 3 2 8
T= I+k+J+L+H+G+D+X