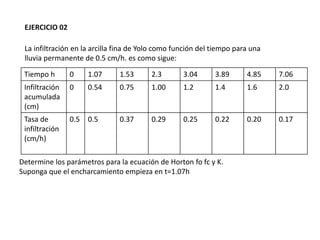
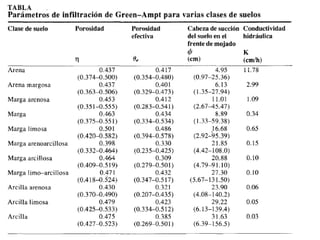
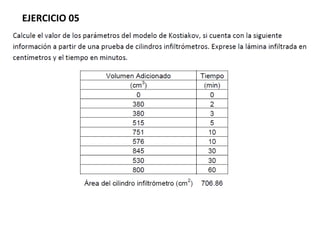
Este documento trata sobre la infiltración del agua en el suelo. Explica conceptos como la tasa de infiltración, lámina de infiltración acumulada, ecuaciones de Philip-Horton y Green-Ampt para modelar la infiltración. Incluye figuras sobre el destino del agua de lluvia y zonas del suelo, así como métodos para medir la infiltración usando infiltrómetros. Contiene también ejemplos y ejercicios resueltos sobre el cálculo de la infiltración usando las ecuaciones.

1. 1
Hidrología: Infiltración
Mario Aguirre Núñez

2. CONTENIDOS TEMÁTICOS
 Tasa de infiltración
 Lámina acumulada de Infiltración
 Ecuación Philips-Horton
 Infiltración Green Ampt

4. Shaxson, 2001 según FAO, 1995b.

5. FIGURA 3
La secuencia de los destinos del agua de lluvia
Leyenda:
1. Evaporación directa de las superficies húmedas
de las hojas.
2. Escorrentía superficial/tormentas.
3. Evaporación directa de la superficie del suelo
4,5,6. Humedad del suelo disponible para las
plantas al alcance de las raíces de las malezas,
cultivos, árboles existentes.
7. Humedad del suelo al alcance de las raíces de
las plantas existentes pero retenida a tensiones
indisponibles para los mismos.
8. Humedad del suelo retenida a cualquier tensión
pero debajo de las raíces de las plantas existentes.
9. Agua no capturada por las raíces y los poros
pequeños moviéndose a agua subterránea y flujo
de corrientes.
10. Lixiviación a agua subterránea debajo del piso
de captura.
Shaxson, 2001 según FAO, 1995b.

7. INFILTRACIÓN
Zona no
saturada
Zona
saturada

9. https://www.youtube.com/watch?v=tLXblDzpBVI

11. Medición de la infiltración (tasa de infiltración, tasa de infiltración potencial)
En general, el perfil hídrico del medio poroso puede representarse esquemáticamente tal
como puede observarse en la figura. Entre la superficie del terreno y el plano que
representa al nivel freático (aquella superficie saturada con un valor de presión igual al de
la atmósfera) se encuentra la zona no saturada o zona vadosa, con valores de presión
menores a la atmosférica (tensión).
Ahora bien, dependiendo de la textura del medio poroso, se podrá desarrollar en la zona
vadosa una franja cercana al nivel freático denominada franja capilar, en la cual los valores
de presión son muy cercanos a la presión atmosférica, sin llegar a la igualdad.
La condición de no saturación en la
zona vadosa puede cambiar con el
tiempo, ya que al ocurrir la
infiltración se puede alcanzar la
saturación.
Infiltracion. - YouTube

12. Medición de la magnitud de la infiltración (tasa de infiltración, tasa de
infiltración potencial)
La obtención del valor de la infiltración, o capacidad de infiltración,
depende de mediciones volumétricas y de área en un determinado
tiempo; para ello se consideran las situaciones siguientes:
1. Mantener en un área muy reducida una lámina de agua fija
definida sobre la superficie del terreno durante un intervalo de
tiempo; infiltrómetro
2. Medir en un área reducida la variación en el tiempo de una
lámina inicial; infiltrómetro
3. Emplear en un área reducida un simulador de lluvia;
4. Hacer una medición de la variación de la tensión mátrica y/o del
contenido de humedad en una zona extensa cuando se presentan
las lluvias;
5. A nivel cuenca, se puede estimar un valor representativo de
infiltración a través del análisis de hidrogramas.

14. Cómo utilizar el infiltrómetro de doble anillo | | UPV - YouTube

15. Ejercicio
Los resultados de una prueba de un cilindro infiltrómetro simple,
constituido de un tubo de 35 cm de diámetro y 50 cm de largo,
fueron:
Tiempo (min) 2 6 14
Volumen Agua (cm3) 250 500 655
Determinar la curva de variación de la capacidad de infiltración

16. Ejercicio
Los resultados de una prueba de un cilindro infiltrómetro simple,
constituido de un tubo de 35 cm de diámetro y 50 cm de largo,
fueron:
Tiempo (min) 2 6 14
Volumen Agua (cm3) 250 500 655
Determinar la curva de variación de la capacidad de infiltración
𝑡𝑎𝑠𝑎 𝑖𝑛𝑓𝑖𝑙𝑡𝑟𝑎𝑐𝑖ó𝑛 =
ΔV
A Δt

17. Ejercicio
Los resultados de una prueba de un cilindro infiltrómetro simple,
constituido de un tubo de 35 cm de diámetro y 50 cm de largo,
fueron:
Tiempo (min) 2 6 14
Volumen Agua (cm3) 250 500 665
Determinar la curva de variación de la capacidad de infiltración
𝑡𝑎𝑠𝑎 𝑖𝑛𝑓𝑖𝑙𝑡𝑟𝑎𝑐𝑖ó𝑛 =
ΔV
A Δt

18. Ejercicio Determinar la curva de variación de la capacidad de infiltración
0
10
20
30
40
50
60
70
80
90
0 2 4 6 8 10 12 14 16
Variación capacidad de Infiltración

20. MÉTODOS PARA CALCULAR LA INFILTRACIÓN
El análisis cuantitativo de la infiltración se puede llevar a cabo
utilizando la ecuación de Richards, considerada como el modelo
matemático representativo del fenómeno del flujo en el medio
poroso no saturado, a partir de la ecuación:
donde ∇ es el operador nabla.
La solución general de la ecuación es difícil, de modo que se ha
resuelto para casos muy particulares, obteniendo así los métodos
básicos para la cuantificación de la infiltración. A continuación se
presentan algunos de los métodos más representativos.

21. S Coeficiente de adsorción cm*h^0.5
t tiempo en horas
K Conductividad hidráulica cm/h
S es función del potencial de succión del suelo
F(t) lámina de agua infiltrada en cm.
S es la sorptividad, que depende de la tensión mátrica ψ del suelo

25. Suponga que los parámetros para la ecuación de Philip son adsorción
S= 5 cm *h ^-0.5 y K = 0.4 cm/h .
Determine la infiltración acumulada después de 0;0.5;1.0;1.5; y 2.0 h.
Suponga condiciones de encharcamiento continuo.
Grafique
a) Tasa de infiltración vs tiempo
b) Infiltración acumulada vs tiempo
c) Tasa de infiltración vs infiltración Acumulada
Ecuación de Philips
Ejercicio 01

26. Los parámetros de la ecuación de Philip para un suelo arcilloso son
S= 45 cm*h^-0.5 y K = 10 cm/h .Determine la infiltración acumulada y la tasa de
Infiltración en incrementos de 0.5 horas durante un periodo de 3 horas.
Suponga condiciones de encharcamiento continuo. Además grafique
Tasa de infiltración vs infiltración Acumulada.
Los parámetros de la ecuación de Philip para un suelo arenoso son
S= 9.0 cm*h^-0.5 y K = 10 cm/h .Determine la infiltración acumulada y la tasa de
Infiltración en incrementos de 0.5 horas durante un periodo de 3 horas.
Suponga condiciones de encharcamiento continuo. Además grafique
Tasa de infiltración vs infiltración Acumulada.
Ejercicio 02
Ejercicio 03
Ecuación de Philips

27. La infiltración en la arcilla fina de Yolo como función del tiempo para una
lluvia permanente de 0.5 cm/h. es como sigue:
Tiempo h 0 1.07 1.53 2.3 3.04 3.89 4.85 7.06
Infiltración
acumulada
(cm)
0 0.54 0.75 1.00 1.2 1.4 1.6 2.0
Tasa de
infiltración
(cm/h)
0.5 0.5 0.37 0.29 0.25 0.22 0.20 0.17
Determine parámetros de la ecuación de Philip.
Suponga que el encharcamiento empieza en t=1.07h
Ejercicio 04
Ecuación de Philips

28. f(t) tasa de infiltración cm/h
fc es tasa de infiltración cuando t tiende infinito cm/h
t tiempo en horas
k Constante de decaimiento h-1
fo es tasa de infiltración inicial t=0 cm/h

29. Ecuación de Horton: Ejercicio
La capacidad de infiltración inicial de una Cuenca se ha estimado en 3.75 cm/h. la
constante k en 0.35 h-1 y la capacidad de infiltración de equilibrio en 0.5 cm/h. Con
la ecuación de Horton determinar:
a) Los valores de infiltración f a 10 min, 30 min, 1 hora, 2 h y 6 h.
b) La lámina total infiltrada durante el período de 6 horas

30. Ecuación de Horton: Ejercicio
La capacidad de infiltración inicial de una Cuenca se ha estimado en 3.75 cm/h. la
constante k en 0.35 h-1 y la capacidad de infiltración de equilibrio en 0.5 cm/h. Con
la ecuación de Horton determinar:
a) Los valores de infiltración f a 10 min, 30 min, 1 hora, 2 h y 6 h.
b) La lámina total infiltrada durante el período de 6 horas

31. Ecuación de Horton

38. EJEMPLO

39. Procedimiento 01

40. Procedimiento 02

41. procedimiento 03

42. Verificar cálculo unidades a trabajar

44. EJERCICIO
además

45. TAREA 01
TAREA 02
TAREA 03

46. La tasa de infiltración como función del tiempo para una marga limosa
de Alexis es como sigue:
Tiempo h 0 0.07 0.016 0.27 0.43 0.67 1.10 2.53
Tasa de
infiltración
(pulg/h)
0.26 0.21 0.17 0.13 0.09 0.05 0.03 0.01
Determine los mejores valores para los parámetros de la ecuación de horton fo fc y K
para describir la infiltración en la marga limosa de Alexis
EJERCICIO 01

47. La infiltración en la arcilla fina de Yolo como función del tiempo para una
lluvia permanente de 0.5 cm/h. es como sigue:
Determine los parámetros para la ecuación de Horton fo fc y K.
Suponga que el encharcamiento empieza en t=1.07h
EJERCICIO 02
Tiempo h 0 1.07 1.53 2.3 3.04 3.89 4.85 7.06
Infiltración
acumulada
(cm)
0 0.54 0.75 1.00 1.2 1.4 1.6 2.0
Tasa de
infiltración
(cm/h)
0.5 0.5 0.37 0.29 0.25 0.22 0.20 0.17

48. Ejercicio 03

49. 𝜓:Cabeza de succión de suelo en el frente de mojado
∆𝜃 = 𝜂- 𝜃𝑖 cambio en el contenido de humedad
diferencia entre los contenidos de humedad del suelo inicial y
final
K: conductividad hidráulica
𝜂: porosidad
ℎ𝑜:
𝜃𝑒 = 𝜂- 𝜃𝑟 : porosidad efectiva máximo contenido de
humedad posible
𝜃𝑖:
𝜃𝑟: contenido residual de humedad del suelo

50. De la ecuación de continuidad y de la ecuación de momentum y la ecuación de Darcy
𝜓:Cabeza de succión de suelo en el frente de mojado
∆𝜃 = cambio en el contenido de humedad
diferencia entre los contenidos de humedad del suelo inicial y
final
K: conductividad hidráulica
El agua se encharca en la superficie del suelo hasta una profundidad pequeña ho
que se considera ho despreciable

51. (1 ) y ( 2 )
Reemplazar lo indicado

52. Excel datos f objetivo listo
Se hace el cálculo de F(t) para un tiempo conocido t
para un determinado valor de t

53. ( I )
𝜓:Cabeza de succión de suelo en el frente de mojado
𝑆𝑒: saturación efectiva, dato de laboratorio
K, 𝜃𝑒, 𝜓 valores de tabla de acuerdo al tipo de suelo
∆𝜃 = 𝜂- 𝜃𝑖 cambio en el contenido de humedad

54. A

55. para t = 1hora calcule F(1) y f(1)

58. Resolución excel classpad fx570 casio t= 1hora F(1) = 3.17 cm.
f(1) = 1.81 cm/h

60. EJERCICIO 01
Utilice el método de Green Ampt para evaluar la tasa de infiltración y la profundidad de
infiltración acumulada para un suelo limo –arcilloso en intervalos de 0.1 horas desde el
principio de la infiltración y durante 6 horas.
Suponga una saturación efectiva inicial del 20% y un encharcamiento continuo.
Utilice el método de Green Ampt calcule la infiltración acumulada para un suelo limo –
arcilloso después de una hora para saturaciones efectivas iniciales de 0,20,40,60,80 y 100%.
Dibuje una gráfica de infiltración acumulada vs saturación efectiva inicial.

61. Utilizando los valores de parámetros daos en la tabla mostrada, determine puntos
en las curvas de tasa de infiltración para arena, marga, marga arcillosa y arcilla desde
el tiempo 0 hasta 4 horas, para intervalos de 0.5 h. Grafique y compare estas curvas.
Suponga una saturación efectiva inicial del 30% para cada suelo y un encharcamiento
continuo.
EJERCICIO 02

62. Utilizando los valores de parámetros daos en la tabla mostrada, determine puntos
en las curvas de infiltración acumulada para arena, marga, marga arcillosa y arcilla desde
el tiempo 0 hasta 4 horas, para intervalos de 0.5 h. Grafique y compare estas curvas.
Suponga una saturación efectiva inicial del 30% para cada suelo y un encharcamiento
continuo.
EJERCICIO 03

63. Utilizando los valores de parámetros daos en la tabla mostrada, determine puntos
en las curvas de tasa de infiltración para arena, marga, marga arcillosa y arcilla desde
el tiempo 0 hasta 4 horas, para intervalos de 0.5 h. Grafique y compare estas curvas.
Suponga una saturación efectiva inicial del 15% para cada suelo y un encharcamiento
continuo.
EJERCICIO 04

64. Utilizando los valores de parámetros daos en la tabla mostrada, determine puntos
en las curvas de infiltración acumulada para arena, marga, marga arcillosa y arcilla desde
el tiempo 0 hasta 4 horas, para intervalos de 0.5 h. Grafique y compare estas curvas.
Suponga una saturación efectiva inicial del 15% para cada suelo y un encharcamiento
continuo.
EJERCICIO 05

67. = 706.86

68. = 706.86

70. Problema TAREA

71. TIEMPO DE ENCHARCAMIENTO

73. I) t< 𝑡𝑝 i (intensidad de lluvia) < 𝑡𝑎𝑠𝑎 𝑑𝑒 𝑖𝑛𝑓𝑖𝑙𝑡𝑟𝑎𝑐𝑖ó𝑛 𝑝𝑜𝑡𝑒𝑛𝑐𝑖𝑎𝑙
𝑠𝑢𝑝𝑒𝑟𝑓𝑖𝑐𝑖𝑒 𝑠𝑢𝑒𝑙𝑜 𝑛𝑜 𝑠𝑎𝑡𝑢𝑟𝑎𝑑𝑎
II ) Empieza encharcamiento i (intensidad de lluvia) > 𝑡𝑎𝑠𝑎 𝑝𝑜𝑡𝑒𝑛𝑐𝑖𝑎𝑙 𝑑𝑒 𝑖𝑛𝑓𝑖𝑙𝑡𝑟𝑎𝑐𝑖ó𝑛
a) En ese momento t= 𝑡𝑝 superficie suelo se satura inicio encharcamiento.
b) Lluvia continua t > 𝑡𝑝 la zona saturada se extiende en el suelo (ℎ𝑜) 𝑦 𝑒𝑚𝑝𝑖𝑒𝑧𝑎 𝑙𝑎
𝑒𝑠𝑐𝑜𝑟𝑟𝑒𝑛𝑡í𝑎 𝑑𝑒𝑙 𝑎𝑔𝑢𝑎 𝑒𝑛𝑐ℎ𝑎𝑟𝑐𝑎𝑑𝑎

74. 𝑡𝑝 tiempo de encharcamiento
i intensidad de lluvia constante
Fp infiltración acumulada

75. 𝑡𝑝 tiempo de encharcamiento
i intensidad de lluvia constante
Fp infiltración acumulada
Fp = i * 𝑡𝑝 además f(𝑡𝑝 )= f=i
luego
Despejar 𝑡𝑝

76. i intensidad de lluvia constante

81. DESPUÉS DEL ENCHARCAMIENTO

82. Cálculo del tiempo de encharcamiento
Cálculo de la infiltración acumulad a para t >tp
Cálculo de la tasa de infiltración
Cálculo de la infiltración acumulad a para t = tp t0 es cero
Fp = i * 𝑡𝑝 además f(𝑡𝑝 )= f=i

84. Segunda parte

85. Primera parte

86. Tercera parte
t> tp F( 1) = 3.02 cm
Por solver se calcula

87. Para
t =1h > tp F(1) = 1.87 cm/h

88. Diferencia entre estos 02 ejemplos

101. PROBLEMAS PROPUESTOS 4.4
TAREA

102. PROBLEMAS PROPUESTOS
TAREA

103. TAREA

104. CONCLUSIONES
➢Concepto de Infiltración
➢Tasa de infiltración y lámina de infiltración
➢Infiltración potencial e infiltración real
➢Fórmulas para la estimación de la infiltración
➢Ejercicios para la estimación de f y de F

105. 105
Gracias

106. EJERCICIO 05