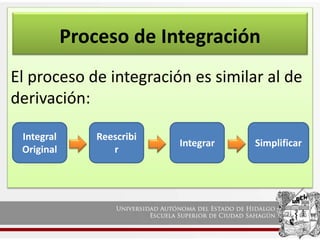
Este documento presenta fórmulas y ejemplos de integración. Explica cómo encontrar la función primitiva de una derivada mediante la integración indefinida, y cómo resolver ecuaciones diferenciales mediante la notación de primitivas. También define conceptos clave como la constante de integración y el proceso general de integración.

1. Cálculo Diferencial e Integral
Integrales
Área Académica: Ingeniería Mecánica
Profesor(a): M. en C. Yira Muñoz Sánchez
Periodo: Enero – Junio 2015

2. Cálculo Diferencial e Integral
Resumen
En este material se presentan fórmulas de integración y
ejemplos de su aplicación.
Abstract
This material presents integration formulas and
examples for appling.
Keywords: integration formulas, integration, examples
integration .

3. Se pide encontrar la función f, cuya derivada
es:
𝒇´(𝒙) = 𝟑𝒙𝟐
Integración

4. Se podría considerar:
f ′(𝐱) = 𝟑𝐱𝟐, ya que
𝐝
𝐝𝐱
𝐱𝟑 = 𝟑𝐱𝟐
La función F es una primitiva o antiderivada de f
en un intervalo I si F’(x) = f(x) para todo x en I.
Primitiva o antiderivada

5. Primitivas de 𝟑𝐱𝟐 :
F1(𝐱) = 𝒙𝟑
F2(𝐱) = 𝒙𝟑
- 5
F3(𝐱) = 𝒙𝟑
+ 97
Familia de Primitivas
Para cualquier valor de la
constante C, F(𝐱) = 𝒙𝟑+
C es primitiva de f y C es
llamada constante de
integración.

6. Para la ecuación diferencial:
𝐆′
𝐱 = 𝟐𝐱
La solución general (primitiva general) es:
Ejemplo 1

7. Para la ecuación diferencial:
𝒚′
= 𝟐
Ejemplo 2
1.- Hallar una función
cuya derivada sea 2:
𝐲 = 𝟐𝐱
2.- Sumar la constante
de integración:
𝐲 = 𝟐𝐱 + 𝐂

8. Al resolver una ecuación diferencial de la
forma:
𝑑𝑦
𝑑𝑥
= 𝑓(𝑥)
conviene más expresarla en la forma:
𝒅𝒚 = 𝒇 𝒙 𝒅𝒙
Notación de la Primitivas

9. El proceso u operación de hallar todas las
soluciones de la ecuación:
𝒅𝒚 = 𝒇 𝒙 𝒅𝒙
se llama Integración Indefinida o
antiderivación y se denota por el signo
integral: ʃ
INTEGRACIÓN INDEFINIDA (1)

10. 𝐲 = 𝐟 𝐱 𝐝𝐱 = 𝐅 𝐱 + 𝐂
INTEGRACIÓN INDEFINIDA (2)
Integrando
Variable de
Integración
Constante de
Integración

11. La expresión:
𝐟 𝐱 𝐝𝐱
se lee: « la integral indefinida de f con
respecto a x »
INTEGRACIÓN INDEFINIDA (3)

12. El proceso de integración es similar al de
derivación:
Proceso de Integración
Integral
Original
Reescribi
r
Integrar Simplificar

13. Referencias
LARSON E. R., HOSTETLER R.P., EDWARDS B. H.,
Cálculo y Geometría Analítica, Sexta Edición, Volumen 1, Mc
Graw Hilll.
STEWART J. , Introducción al Cálculo, Thomson
STEWART J. , Calculus. Early Trascendentals, Sixth
Edition, Thomson