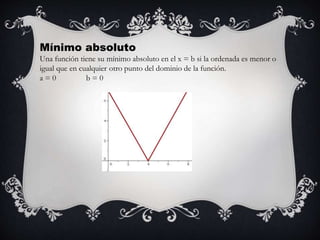
La integral indefinida es el conjunto de las infinitas primitivas que puede tener una función. Se representa por ∫ f(x) dx y se lee como "integral de f de x diferencial de x". Si F(x) es una primitiva de f(x), entonces ∫ f(x) dx = F(x) + C, donde C es la constante de integración. El teorema fundamental del cálculo establece que la derivada de la integral de una función es igual a la función original.

1. INTEGRAL INDEFINIDA
EPO #56 GRUPO:603
CALCULO IN TEGRAL
INTEGRAL INDEFINIDA
INTEGRANTES: KARLA NAVA NAVA
ROSA ISELA GARCIA GOMEZ
LIDIA GUADALUPE BARRIOS VENTURA
MARIA DANIELA RIVERA DAVILA
LAURA IRINEO DE JESUS

2. INTRODUCCIÓN
 Con este trabajo podemos entender mas sobre la estructura del calculo
integral
 Unos de los aportadores del calculo integral fue Arquímedes, ya que fue el
que aporto lo siguiente:
1)primer teorema fundamental del calculo
2)segundo teorema fundamental del calculo
 Además contiene algunas formulas y teoremas que nos ayudan fácilmente a
resolver problemas

8. TEOREMA
 Es una proposición que firman una verdad general
mente posee un numero de premisa de ve ser
enumeradas o aclaradas ante mano.
 Considera la función continua f(x)en el intervalo
cerrado [a,b]de tal forma 9 f(x) sea la integral indefinida
de f(x)

9. PRIMITIVA
 Función primitiva o antiderivada de una función dada f(x), es otra
función F(x) cuya derivada es la función dada.
 F'(x) = f(x)
 Si una función f(x) tiene primitiva, tiene infinitas primitivas,
diferenciándose todas ellas en una constante.
 [F(x) + C]' = F'(x) + 0 = F'(x) = f(x)

10. DIFERENCIAL
 La operación a encontrar una derivada también
tiene una inversa que se llamaría antiderivada lo
inverso por ejemplo una multiplicación es una
división inversa al elevar al cuadrado
 la diferencial de una función es igual a la derivada
de la función multiplicada por dx : df(x)

11. ANTIDERIVADA
 La operación a encontrar una derivada también
tiene una inversa que llamaremos antiderivada es lo
inverso por ejemplo una multiplicación es la división
inversa de elevar al cuadrado

12. INTEGRANDO
 Integración
 Integrar es el proceso recíproco del de derivar, es decir, dada una función
f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x).
 Se dice, entonces, que F(x) es una primitiva o anti derivada de f(x); dicho de
otro modo las primitivas de f(x) son las funciones derivables F(x) tales que:
 F'(x) = f(x).
 Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose
todas ellas en una constante.
 [F(x) + C]' = F'(x) + 0 = F'(x) = f(x)

13. Integral indefinida
Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee : integral de f de x diferencial de x.
∫ es el signo de integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.
C es la constante de integración y puede tomar cualquier valor numérico real.
Si F(x) es una primitiva de f(x) se tiene que:
∫ f(x) dx = F(x) + C
Para comprobar que la primitiva de una función es correcta basta con derivar.

14. Propiedades de la integral indefinida
1. La integral de una suma de funciones es igual a
la suma de las integrales de esas funciones.
∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx
2. La integral del producto de una constante por
una función es igual a la constante por la integral
de la función.
∫ k f(x) dx = k ∫f(x) dx

15. DERIVADA
 La derivada de la función f aquella función denotada
por la f :tal que su valor en un numero x del dominio de
f esto lado por :
 F(x1)= lim-f(x)+(x)-f(x)

16. Integral indefinida
Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee : integral de f de x diferencial de x.
∫ es el signo de integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.
C es la constante de integración y puede tomar cualquier valor numérico real.
Si F(x) es una primitiva de f(x) se tiene que:
∫ f(x) dx = F(x) + C
Para comprobar que la primitiva de una función es correcta basta con derivar.
Propiedades de la integral indefinida
1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx
2. La integral del producto de una constante por una función es igual a laconstante por la
integral de la función.
∫ k f(x) dx = k ∫f(x) dx

17. Máximo absoluto
Una función tiene su máximo absoluto en el x = a si la ordenada es mayor o
igual que en cualquier otro punto del dominio de la función.

18. Valor de una función dada, que es mayor o igual que cualquier valor de
la función dada. El máximo absoluto es el mayor de todos los valores.

19. Mínimo absoluto
Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o
igual que en cualquier otro punto del dominio de la función.
a = 0 b = 0

20. Valor de una función que es menor o igual a cualquier valor de la función
dada. El mínimo absoluto es el menor de todos los valores.

21. Máximo y mínimo relativo
Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual
que los puntos próximos al punto a.
Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual
que los puntos próximos al punto b.
a = 3.08 b = -3.08

22. Máximo local (máximo relativo)
Valor de una función que es mayor que los valores de la función en puntos
cercanos, pero que no es el mayor de todos los valores.

23. Mínimo local (mínimo relativo)
Valor de una función, que es menor que los valores de la función en puntos
cercanos, pero que no es el menor de todos los valores.

24. Evaluar
Significa pedirle a la función que transforme un numero. El valor que le
damos, lo
sustituimos en la función y hacemos los cálculos que quedan indicados.
Por ejemplo, vamos a evaluar la función y = x
2 + 2x −4 en x = 3.
y = (3)2 + 2 (3)−4
Significa pedirle a la función que transforme un numero. El valor que le
damos, lo
sustituimos en la función y hacemos los cálculos que quedan indicados.
Por ejemplo, vamos a evaluar la función y = x
2 + 2x −4 en x = 3.
y = (3)
2 + 2 (3)−4= 9 + 6−4= 11
Sustituimos el valor de x donde encontremos x en la función...

25. Por ejemplo, vamos a evaluar la función y = x2 + 2x −4 en x = 3.
y = (3)2 + 2 (3)−4
= 9 + 6−4
Sustituimos el valor de x donde encontremos x en la función...
Hacemos los cálculos que quedaron indicados
Por ejemplo, vamos a evaluar la función y = x
2 + 2x −4 en x = 3.
y = (3)
2 + 2 (3)−4
= 9 + 6−4
= 11
Sustituimos el valor de Hacemos los cálculos que quedaron indicados x donde
encontremos x en la función...
Al simplificar, encontramos el valor que nos devuelve la función.

26. TEOREMA FUNDAMENTAL
DE CALCULO
Consiste en la afirmación de la que la derivación e
integración de una función son operaciones inversas
,esto significa que toda función acotada e integrable
(siendo continuo o discontinuo en un numero finito de
un punto) verifica que la derivada de su integral es
igual a ella misma entre teoremas, es central en la
rama de las matemáticas denominada análisis
matemático o calculo

27. LA DERIVADA E INTEGRAL
COMO PROCESO INVERSO
 Por lo que realizamos primero un proceso y luego el otro
obtendríamos la función inicial . Es importante por lo que en muchas
ocasiones las soluciones diferencial debe dejarse en forma integral por
lo que para estudiar su crecimiento y descrecimiento debemos derivar
esa integral y estudiar el signo de esta derivada y tomando en cuenta
de gran cantidad de proceso naturales están corregidos por ecuaciones
diferenciales parece buena idea saber hacer eso

28. L A INTE GRAL INDE FINIDA COMO UNA
FAMIL IA D E FUN CION E S
 Dada una función f definida en un intervalo I se dice que otra función F es una
primitiva de f en I si F es derivable en I y F'=f en I.
 Si consideramos la función f(x)=2x, las funciones
 son primitivas de f pues la derivada de cada una de ellas es 2x.
 Dada una función f, no existe para ella una única primitiva F, ya que cualquier otra
función de la forma F+C, donde C es una constante, también cumple la condición de que
su derivada es igual a f
 Además, si F y G son primitivas de f en I entonces F-G=C (constante) en I pues

29.  Las primitivas de una función forman una familia de funciones cuya
representación gráfica es siempre la misma, estando cada una desplazada
verticalmente respecto de las demás:
 Al conjunto de todas las primitivas de una función f se le llama integral
indefinida de f y se representa por
 Para f(x)=2x se tiene
 Teniendo en cuenta las derivadas de las funciones f "elementales"
(potencias, exponenciales, trigonométricas, y sus inversas) obtenemos las
siguientes integrales indefinidas:

30.  Las igualdades anteriores son ciertas cuando las expresiones que aparecen en ellas tienen sentido. Así, por ejemplo
 Para f(x)=1/x en I=(0,+∞) tenemos
 Sin embargo en I=(- ∞,0) obtenemos
 Propiedades de la integral indefinida
 Se verifica:
 Estas propiedades son consecuencia de la linealidad de la derivación:
 Utilizando la propiedad de linealidad de la integral indefinida y las primitivas de funciones sencillas podemos
calcular la siguiente integral:
 La generalización de estos resultados aparece en la tabla de integración inmediata.

32. CONCLUCION
Nos ayudo a saber mas sobre las diferentes temas que aborda este
trabajo, ya que nos dimos cuenta que el calculo integral esta formado
por muchos otros elementos con los que se nos hace mas fácil
calcular problemas mediante sus diferentes formulas y teoremas
Además nos ayudo a entender un poco mas el significado de algunas
palabras que antes no entendíamos

33. BIBLIOGRAFÍAS
 www.mathematicsdiccionary.com./spanish/vmd/full/ocalminimu
nrelativeminimum.http
 www.vitutor.com/fun/2/a_9.html
 www.ditutor.com/calculointegral/0087/fun.http