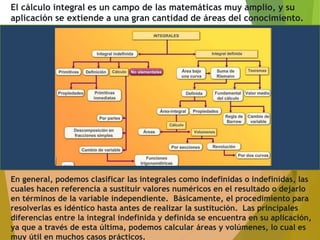
El documento trata sobre el tema de las integrales. Explica brevemente qué es una integral indefinida y definida, y cómo se utilizan para calcular áreas y volúmenes. Luego, detalla algunas propiedades y fórmulas básicas para calcular integrales indefinidas de funciones como polinomios, exponenciales, logaritmos, senos y cosenos. Finalmente, introduce algunos métodos para calcular integrales más complejas, como la integración por partes y el cambio de variable.

2. Un par de subtemas:
 Saber que es una Integral.
 Calcular una integral con
ciertas funciones.
 Utilizar el concepto de
integral para calcular áreas.

3. El cálculo integral es un campo de las matemáticas muy amplio, y su
aplicación se extiende a una gran cantidad de áreas del conocimiento.
En general, podemos clasificar las integrales como indefinidas o indefinidas, las
cuales hacen referencia a sustituir valores numéricos en el resultado o dejarlo
en términos de la variable independiente. Básicamente, el procedimiento para
resolverlas es idéntico hasta antes de realizar la sustitución. Las principales
diferencias entre la integral indefinida y definida se encuentra en su aplicación,
ya que a través de esta última, podemos calcular áreas y volúmenes, lo cual es
muy útil en muchos casos prácticos.

4. La Integral Indefinida.

5. Y está definida por la propiedad
Lo opuesto a una derivada es una antiderivada o
integral indefinida.
La integral indefinida de una función f(x) se
denota como
Integral indefinida
Esto quiere decir que la integral es la operación
inversa de la derivada.

6. • Para resolver una integral, solo debemos aplicar la fórmula
que coincida con la estructura de la función.
• Sin embargo, para que la función coincida con la fórmula,
debemos asegurarnos de que el término dx sea la diferencial
de x. De no ser así, debemos “completar” la integral. Por
ejemplo,
Existen dos aspectos muy importantes que debemos tomar
en cuenta para resolver integrales:
La diferencial de x es dx, por lo tanto la integral
está “completa” y podemos aplicar la fórmula
correspondiente.
La diferencial de 2x es 2dx. Para que la integral esté
“completa” le falta un 2 a dx y es necesario
completarla. Si colocamos un 2 como numerador,
debemos agregar también un 2 como denominador para que
la función no se altere. Es decir, es como si
multiplicáramos la función por 1 (en este caso, 2/2).
La función quedaría de la siguiente forma después de
completarla:

7. • Si la integral fuera
La diferencial de -2x es -2dx. Para que la integral
esté “completa” le falta un -2 a dx y es necesario
completarla. Si colocamos un -2 como numerador,
debemos agregar también un -2 como denominador para
que la función no se altere. La función quedaría de la
siguiente forma después de completarla:

8. • Cuando calculamos la integral de una función,
suponemos que dicha función es el resultado de una
derivada, así que lo que estamos obteniendo mediante
la integral es la función original antes de
derivarla.
• Debido a que la derivada de una constante es cero, no
es posible saber si existía o no alguna constante
dentro de la función original.
• Es por eso que una función tiene un número infinito
de integrales, que difieren por una constante
aditiva. Por eso al resultado siempre le debemos
sumar una constante C. En las diapositivas
siguientes aprenderemos más sobre esta propiedad.
Otro aspecto muy importantes que debemos tomar
en cuenta es que si

9. donde C es una constante arbitraria.
La integral indefinida de una función cuya
derivada es idénticamente cero
La integral indefinida de una función idénticamente
cero es una constante
La integral de una función
idénticamente cero.

10. Función constante
La integral indefinida de una constante.
La integral indefinida de la función constante:
Donde c es una constante.

11. La integral indefinida de la función identidad:
La integral indefinida de la función identidad.
Donde c es una constante arbitraria.

12. La integral indefinida de la función es:
La integral indefinida de una potencia de x.
Donde c es una constante arbitraria.

13. La integral indefinida de una potencia de 1/x.
Para una función de la forma
Dado que
Entonces:

14.   2
xxf Miembros de la familia de anti-derivadas de
3
3
3

x
2
3
3

x
1
3
3

x
3
3
x
1
3
3
-
x
2
3
3
-
x
x
Interpretación geométrica:
Por eso siempre debemos
agregar al resultado una
constante C, debido a que
no sabemos exactamente
a qué curva representa el
resultado.

15. En la siguiente diapositiva encontrarás
algunas fórmulas inmediatas de
integración, sin embargo, para poder
continuar, es necesario que tengas una
tabla de integrales más completa, la cual
puedes encontrar en cualquier libro de
cálculo o en algún manual de fórmulas
matemáticas.

16. Fórmulas de antiderivadas
Cxdx
x
 ln
1
Cedxe xx

Cxxdx  sencos
Cxxdx  tansec2
Cxxdxx  sectansec
Cxdx
x




1
2
sen
1
1
Cxdx
x




1
2
tan
1
1
Cxxdx  cossen
C
n
x
dxx
n
n




 1
1
1n

17. Propiedades de la Integral
PRIMERA
La integral indefinida de una suma de funciones es igual a la suma de las
integrales indefinidas de las funciones sumandos.
Es decir:
 [ f (x) + g (x) + ...+ k (x)] dx =  f (x) dx +  g (x) dx + ..  k (x) dx.
Ejemplos
 [ 3.x2 + 2.x + 4] dx =  3.x2 dx +  2.x dx +  4 dx = x3 + x2 + 4.x + C
 [ cos x – sen x] dx =  cos x dx +  – sen x dx = sen x + cos x + C
 [ ex + 2x ] dx =  ex dx +  2x dx = ex + (2x / ln 2) + C
 [ 7.x6 + 3x – cos x – 9] dx =  7.x6 dx +  3x dx –  cos x dx –  9 dx =
= x7 + (3x / ln3) – sen x – 9.x + C

18. Propiedades de la integral
SEGUNDA
La integral indefinida del producto de un número (una constante) por una
función f(x) es igual al producto del número (de la constante) por la integral
indefinida de la función f (x).
Simbólicamente:
 k .f (x) dx = k  f(x) dx
Ejemplos
(Ya resueltos al ser integrales inmediatas)
 3.ex dx = 3. ex dx = 3.ex + C
 5.cos x dx = 5. cos x dx = 5.sen x + C
 (5 / x) dx = 5.  (1 / x) dx = 5. ln x + C
 (7 / 16.√x) dx = (7 / 8). (1 / 2.√x) dx = (7 / 8).√x + C

19. Sea la función polinómica f(x)= 11. x5 + 5. x3 - 7. x2 + 7x + 9.
Dicha función es la suma de las funciones
f1(x) = 11. x 5 ; f2(x) = 5. x 3 ; f3(x) = (-7). x 2 ; f4(x) = 7.x ; f5(x)
= 9
Según las propiedades previas :
 [11. x5 + 5. x3 - 7. x2 + 7x + 9 ] dx =
=  11. x5 dx +  5. x3 dx -  7. x2 dx +  7x dx +  9 dx =
11. x6 5. x4 7. x3 7. x2
= ------- + ------- -- ------ + ------ + 9. x + C
6 4 3 2

20. 




ax
dx =
ax
ln a
+ C, para cualquier a > 0
 Para a = e se obtiene




ex
dx = ex
+ C
Tipo general
Ejemplo:




f '(x) af(x) dx =
af(x)
ln a
+ C, para a > 0





x2
ex3
dx =
1
3 



3x2
ex3
dx =
1
3
ex3
+ C

21. 




sen x dx = – cos x + C
Tipo general
Ejemplo:




f '(x) sen f(x) dx = – cos f(x) + C





e3x
sen (e3x
+ 5) dx = 1
3 



3 e3x
sen (e3x
+ 5) dx = –
1
3
cos (e3x
+ 5) + C

22. 




cos x dx = sen x + C
Tipo general
Ejemplo:




f '(x) cos f(x) dx = sen f(x) + C





e7x
cos (e7x
+ 5) dx =
1
7 



7 e7x
cos (e7x
+ 5) dx =
1
7
sen (e7x
+ 5) + C

23.  2
1
arcsen( )
1
dx x C
x
 

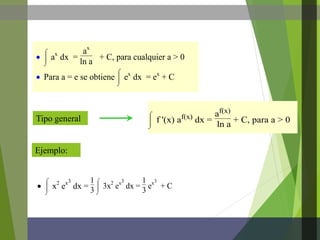
Tipo
general
Ejemplo:


 g '(x)
1 - [g(x)]2 dx = arcsen g(x) + C



 e3x
1 – e6x dx =


 e3x
1 – (e3x
)2
dx =
1
3 

 3e3x
1 – (e3x
)2
dx =
1
3
arcsen e3x
+ C

24. 


 1
1 + x2 dx = arctg x + C
 
2
f ( )
arctg( )
1 f( )
x
dx x C
x

 

Tipo
general



 1
1 + 2x2 dx =
Ejemplo:


 1
1 + ( 2x)2 dx =
1
2 

 2
1 + ( 2x)2 dx =  1
arctg 2x
2
C

25. Métodos de
Integración. 

26. Todas las integrales que coinciden con
alguna de las fórmulas de integración, se
resuelven directamente. Solo debemos
asegurarnos de que la integral está
completa.
Sin embargo, existen algunos problemas en
los cuales no podemos aplicar directamente
alguna fórmula, en cuyo caso, debemos
recurrir a algún método de integración
como los que se presentan a continuación.

27. Integración por partes
De esta forma, la fórmula de la integral por partes
queda de la siguiente forma:
Cuando necesitamos obtener la derivada de un
producto de funciones:
Para simplificar la expresión, es común hacer un
cambio en la notación:

28. Ejemplos de integración por partes:
Algunas ocasiones es necesario aplicar más de una
vez la integral por partes para poder llegar al
resultado:
= x2
ex
– 2[xex
–




ex
dx ] = ex
(x2
– 2x + 2) + C
 



x2
ex
dx =
dvu
x2
ex
–




ex
2x dx = x2
ex
– 2




x ex
dx =
dvu
u = x2  du = 2x dx
dv = ex . dx  v = ex
u = x  du = dx
dv = ex . dx  v = ex

29. Ejemplos de integración por partes:
u = sen (L x)  du = cos(L x) . (1/x) . dx
dv = dx  v = x
= x . sen(ln x) – x cos(ln x) –




sen(ln x) . dx . Despejando la integral buscada queda:
x . sen (ln x) –




cos (ln x) . dx = 



sen(ln x) . dx =
u dv
u = cos (L x)  du = – sen(L x) . (1/x) . dx
dv = dx  v = x
u dv




sen(ln x) . dx =
1
2
x [sen(ln x) – cos(ln x)] + C

30. Integración por sustitución o cambio
de variable:



 1
x ln x
dx
Cambio ln x = u  dx / x = du  dx = x. du = et du
x = eu

=


 1
eu .
u
eu .
du =


 1
u
du = ln | u | + C
deshacer el cambio
= ln | ln x | + C
Para calcular una integral por cambio de variable:
• Buscar una transformación u = g(x) que reduzca su cálculo al de una integral
inmediata.
• Cuando se realiza el cambio debe transformarse también la diferencial
mediante.
du = g'(x) dx
• Después de calcular la integral inmediata debe deshacerse el cambio
poniendo g(x) de nuevo en lugar de u para obtener el resultado final.

31. Ejemplos de integración por sustitución
o cambio de variable:
deshacer el cambio





x3
x4
+ 2 dx =
1
4



4x3
x4
+ 2 dx =
Cambio x4 + 2 = u  4x3 . dx = du
1
4



u du =
1
4
u1/2
1
2
+ 1
+ C =
1
4
(x4
+ 2)3
+ C

32. Ejemplos de integración por sustitución
o cambio de variable:





sen3
2x .
cos 2x dx =
1
2 



t3 .
dt =
Cambio sen 2x = t  2 cos 2x . dx = dt
=
1
8
sen4
2x + C
1
2
t4
4
+ C
deshacer el cambio

33. La Integral Definida.


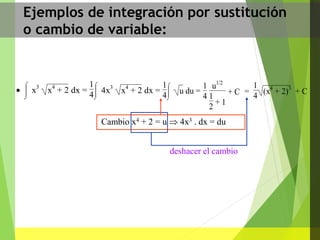
34. La Integral Definida:
Si f es positiva, la integral definida nos da el área de
la región comprendida entre la curva y=f(x) y el eje X, en el
intervalo [a, b].
 
b
a
dxxf
   RAdxxf
b
a

y = f (x)
0
y
x
R
a b Es decir, si sustituimos los
límites señalados en la integral
definida, podemos determinar
el área debajo entre la curva
de la función y el eje x

35. La Integral Definida:
Para calcular la integral definida de una función, el procedimiento es,
en un principio, idéntico al de la integral indefinida, solo que una vez
aplicada la fórmula de integración correspondiente, debemos sustituir
los límites señalados en la integral.
A continuación analizaremos un ejemplo, y, a manera de
procedimiento, plantearemos los siguientes pasos :
1. Resolver la integral:
Dada la integral:
2. Sustituir la variable independiente por el límite superior y hacer lo
mismo con el límite inferior. Restar ambos resultados:
2. Simplificar:

36. Ejemplos de Integral Definida: