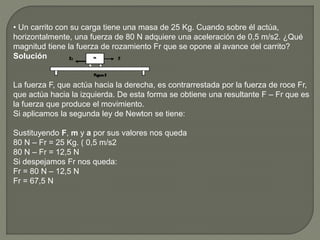
Las leyes de Newton son tres principios fundamentales de la mecánica que explican el movimiento de los cuerpos y son la base de la mecánica clásica. Estas leyes, combinadas con la ley de gravitación universal, permiten entender tanto el movimiento de los astros como el de proyectiles. Autores anteriores a Newton, como Juan de Celaya y Domingo de Soto, ya habían realizado contribuciones significativas al estudio del movimiento y la dinámica que influyeron en la formulación de las leyes de Newton.

1. Alumna: Indira
anaiza Rodríguez
González
c.i:22964691

2. Las leyes de Newton, también conocidas como leyes del
movimiento de Newton, son tres principios a partir de los
cuales se explican la mayor parte de los problemas
planteados por la mecánica, en particular aquellos relativos
al movimiento de los cuerpos, que revolucionaron los
conceptos básicos de la física y el movimiento de los
cuerpos en el universo.
En concreto, la relevancia de estas leyes radica en dos
aspectos: por un lado constituyen, junto con la
transformación de Galileo, la base de la mecánica clásica,
y por otro, al combinar estas leyes con la ley de la
gravitación universal, se pueden deducir y explicar las
leyes de Kepler sobre el movimiento planetario. Así, las
leyes de Newton permiten explicar, por ejemplo, tanto el
movimiento de los astros como los movimientos de los
proyectiles artificiales creados por el ser humano y toda la
mecánica de funcionamiento de las máquinas. Su
formulación matemática fue publicada por Isaac Newton
en 1687 en su obra Philosophiæ naturalis principia
mathematica.

3. La dinámica es la parte de la física que estudia las relaciones entre los
movimientos de los cuerpos y las causas que los provocan, en concreto las
fuerzas que actúan sobre ellos. La dinámica, desde el punto de vista de la
mecánica clásica, es apropiada para el estudio dinámico de sistemas
grandes en comparación con los átomos y que se mueven a velocidades
mucho menores que las de la luz. Para entender estos fenómenos, el punto
de partida es la observación del mundo cotidiano. Si se desea cambiar la
posición de un cuerpo en reposo es necesario empujarlo o levantarlo, es
decir, ejercer una acción sobre él.
Esto motivó que el conocimiento sobre estos hechos fuera erróneo durante
siglos. Aristóteles pensó que el movimiento de un cuerpo se detiene cuando
la fuerza que lo empuja deja de actuar. Posteriormente se descubrió que
esto no era cierto pero el prestigio de Aristóteles como filósofo y científico
hizo que estas ideas perduraran siglos, hasta que científicos como Galileo
Galilei o Isaac Newton hicieron avances muy importantes con sus nuevas
formulaciones. Sin embargo hubo varios físicos que se aproximaron de
manera muy certera a las formulaciones de Newton mucho antes de que
este formulara sus leyes del movimiento.

4. Es el caso del español Juan de Celaya, matemático, físico, cosmólogo,
teólogo y filósofo que en 1517 publicó un tratado titulado In octo libros
physicorum Aristotelis cum quaestionibus eiusdem, secundum triplicem
viam beati Thomae, realium et nominatium, obra de especial interés para el
estudio de los orígenes de la moderna ciencia del movimiento. Durante su
etapa en Francia fue un escritor prolífico, escribiendo sobre todo acerca de
la física de Aristóteles y el movimiento. También publicó numerosos
trabajos sobre filosofía y lógica. Fue uno de los impulsores de la lógica
nominalista y de las ideas mertonianas de los calculadores acerca de la
dinámica. Fue capaz de enunciar, dentro de las Leyes de Newton, la
Primera Ley de o Primer Principio de la Dinámica (una de las leyes más
importantes de la física) un siglo antes que Newton.

5. Escribió numerosas obras de teología, derecho, filosofía y lógica y
también comentó varios libros de física y lógica aristotélica, de los cuales
el más importante fue Quaestiones super octo libros physicorum
Aristotelis (1551), sobre cinemática y dinámica, la cual fue publicada en
varias ciudades italianas, influyendo en personajes como Benedetti o
Galileo. Domingo de Soto fue uno de los primeros en establecer que un
cuerpo en caída libre sufre una aceleración uniforme con respecto al
tiempo dicha afirmación también había sido establecida por Nicolás
Oresme casi dos siglos antes y su concepción sobre la masa fue
avanzada en su época. En su libro Quaestiones explica la aceleración
constante de un cuerpo en caída libre de esta manera:
Este tipo de movimiento propiamente sucede en los graves naturalmente
movidos y en los proyectiles. Donde un peso cae desde lo alto por un
medio uniforme, se mueve más veloz en el fin que en el principio. Sin
embargo el movimiento de los proyectiles es más lento al final que al
principio: el primero aumenta de modo uniformemente disforme, y el
segundo en cambio disminuye de modo uniformemente disforme.

6. Domingo de Soto ya relacionaba dos aspectos de la física: el movimiento
uniformemente disforme (movimiento uniformemente acelerado) y la
caída de graves (resistencia interna). En su teoría combinaba la
abstracción matemática con la realidad física, clave para la comprensión
de las leyes de la naturaleza. Tenía una claridad rotunda acerca de este
hecho y lo expresaba en ejemplos numéricos concretos. Clasificó los
diferentes tipos de movimiento en:
 Movimiento uniforme respecto al tiempo:
Es aquel por el que el mismo móvil en iguales intervalos de tiempo
recorre iguales distancias, como se da perfectamente en el movimiento
extremadamente regular del cielo.
 Movimiento disforme con respecto al tiempo:
Es aquel por el cual, en partes iguales de tiempo son recorridas distancias
desiguales, o en (tiempos) desiguales, (espacios) iguales.

7. Movimiento uniformemente disforme con respecto al
tiempo:
Es el movimiento de tal modo disforme, que si dividimos
según el tiempo, la velocidad de el punto medio de la
proporción excede la velocidad de el extremo más lento lo
que es excedida por el más rápido.
Soto describió el movimiento de caída libre como ejemplo de movimiento
uniformemente acelerado por primera vez, cuestión que solo aparecerá
posteriormente en la obra de Galileo:
Este tipo de movimiento propiamente sucede en los graves naturalmente
movidos y en los proyectiles. Donde un peso cae desde lo alto por un medio
uniforme, se mueve más veloz en el fin que en el principio. Sin embargo el
movimiento de los proyectiles es más lento al final que al principio: el primero
aumenta de modo uniformemente disforme, y el segundo en cambio
disminuye de modo uniformemente diforme.

8. Por lo tanto era aplicable la ley de la velocidad media para calcular el tiempo
de caída:
Esta especie de movimiento es la propia de los cuerpos que se mueven con
movimiento natural y la de los proyectiles.
En efecto, cada vez que cae una masa desde una cierta altura y en el seno de
un medio homogéneo, se mueve al final más de prisa que al principio. Pero el
movimiento de los proyectiles es más lento al final que al comienzo, y así el
primero se intensifica, y el segundo se debilita uniformemente.
Movimiento diformente disforme con respecto al tiempo:
Es el movimiento en tal modo disforme, que si es dividido según el tiempo, no
ocurre que el punto medio de cada parte en la misma proporción excede (en
velocidad) a un extremo cuanto es excedido por el otro. Este tipo de movimiento
es el que esperamos en los animales, donde se observa el aumento y la
disminución.

9. Este fue un descubrimiento clave en física y base esencial para el
posterior estudio de la gravedad por Galileo Galilei e Isaac Newton.
Ningún científico de las universidades de París y Oxford de aquella
época había conseguido describir la relación entre movimiento
uniformemente disforme en el tiempo y la caída de los graves como lo
hizo Soto.
Tras las ideas innovadoras sobre el movimiento de estos científicos,
Galileo hizo un avance muy importante al introducir el método
científico que enseña que no siempre se debe creer en las
conclusiones intuitivas basadas en la observación inmediata, pues
esto lleva a menudo a equivocaciones. Galileo realizó un gran número
de experiencias en las que se iban cambiando ligeramente las
condiciones del problema y midió los resultados en cada caso. De
esta manera pudo extrapolar sus observaciones hasta llegar a
entender un experimento ideal. En concreto, observó cómo un cuerpo
que se mueve con velocidad constante sobre una superficie lisa se
moverá eternamente si no hay rozamientos ni otras acciones externas
sobre él.

10. El primer concepto que maneja Newton es el de masa, que identifica con
cantidad de materia. Newton asume a continuación que la cantidad de
movimiento es el resultado del producto de la masa por la velocidad. En tercer
lugar, precisa la importancia de distinguir entre lo absoluto y relativo siempre
que se hable de tiempo, espacio, lugar o movimiento.
En este sentido, Newton, que entiende el movimiento como una traslación de
un cuerpo de un lugar a otro, para llegar al movimiento absoluto y verdadero de
un cuerpo:
compone el movimiento relativo de ese cuerpo en el lugar relativo en que se lo
considera, con el movimiento relativo del lugar mismo en otro lugar en el que
esté situado, y así sucesivamente, paso a paso, hasta llegar a un lugar inmóvil,
es decir, al sistema de referencias de los movimientos absolutos.

11. Esta ley postula, por tanto, que un cuerpo no puede
cambiar por sí solo su estado inicial, ya sea en reposo o
en movimiento rectilíneo uniforme, a menos que se
aplique una fuerza o una serie de fuerzas cuya resultante
no sea nula. Newton toma en consideración, así, el que
los cuerpos en movimiento están sometidos
constantemente a fuerzas de roce o fricción, que los frena
de forma progresiva, algo novedoso respecto de
concepciones anteriores que entendían que el movimiento
o la detención de un cuerpo se debía exclusivamente a si
se ejercía sobre ellos una fuerza, pero nunca entendiendo
como tal a la fricción.
Esta ley se encarga de cuantificar el concepto de fuerza.
La aceleración que adquiere un cuerpo es proporcional a la
fuerza neta aplicada sobre el mismo. La constante de
proporcionalidad es la masa del cuerpo que puede ser o no
ser constante. Entender la fuerza como la causa del
cambio de movimiento y la proporcionalidad entre la fuerza
impresa y el cambio de la velocidad de un cuerpo es la
esencia de esta segunda ley.

12. Esta tercera ley de Newton es completamente
original pues las dos primeras ya habían sido
propuestas de otra manera por Galileo, Hooke y
Huygens y hace de las leyes de la mecánica un
conjunto lógico y completo. Expone que por cada
fuerza que actúa sobre un cuerpo, este realiza una
fuerza de igual intensidad, pero de sentido
contrario sobre el cuerpo que la produjo. Dicho de
otra forma, las fuerzas, situadas sobre la misma
recta, siempre se presentan en pares de igual
magnitud y de dirección, pero con sentido opuesto.
Si dos objetos interaccionan, la fuerza F, ejercida
por el objeto 1 sobre el objeto 2, es igual en
magnitud con misma dirección pero sentidos
opuestos a la fuerza F ejercida por el objeto 2
sobre el objeto 1.

13. •
Un cuerpo pesa en la tierra 60 Kp. ¿Cuál será a su peso en la luna, donde la
gravedad es 1,6 m/s2?
Datos
PT= 60 Kp. = 588 N
PL =?
gL = 1,6 m/s2
Solución
Para calcular el peso en la luna usamos la ecuación
Como no conocemos la masa, la calculamos por la ecuación:
que al despejar m tenemos:
Esta masa es constante en cualquier parte, por lo que podemos usarla en la
ecuación (I):

14. • Un carrito con su carga tiene una masa de 25 Kg. Cuando sobre él actúa,
horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué
magnitud tiene la fuerza de rozamiento Fr que se opone al avance del carrito?
Solución
La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr,
que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es
la fuerza que produce el movimiento.
Si aplicamos la segunda ley de Newton se tiene:
Sustituyendo F, m y a por sus valores nos queda
80 N – Fr = 25 Kg. ( 0,5 m/s2
80 N – Fr = 12,5 N
Si despejamos Fr nos queda:
Fr = 80 N – 12,5 N
Fr = 67,5 N

15. • Calcular la masa de un cuerpo, si fuerza de atracción entre dos masas es de
1,8 ( 10-2 N y la masa de una de ellas 0,6 ( 102 Kg., y las separa una distancia
de 0,2 ( 10-1 m.
Solución
F = 1,8 ( 10-2 N
M1 = 0,6 ( 102 Kg.
M2 =?
d = 0,2 ( 10-1 m
Despejando M2 de la fórmula de la cuarta ley de Newton tenemos
Sustituyendo en la fórmula los valores tenemos: