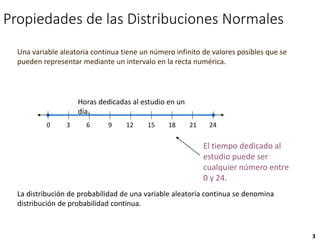
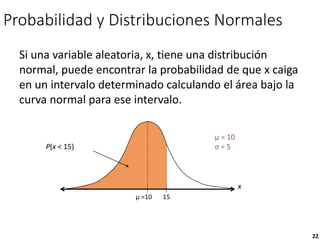
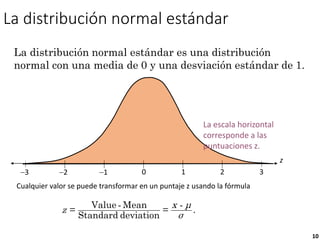
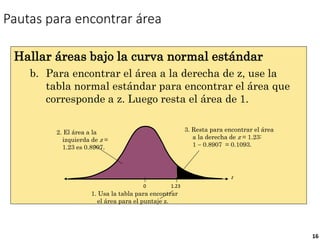
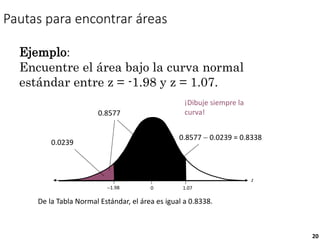
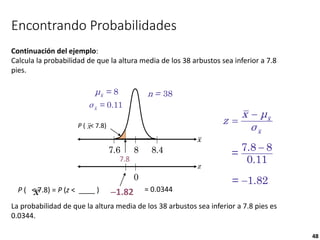
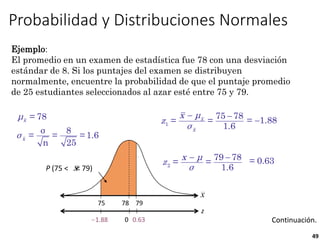
1) La distribución normal es la distribución de probabilidad más importante en estadística y describe cómo se distribuyen muchas variables en la naturaleza. 2) Una variable aleatoria continua tiene una distribución normal si su gráfica tiene forma de campana y está simétrica con respecto a su media. 3) Es posible calcular probabilidades bajo la curva normal usando tablas que relacionan las áreas bajo la curva normal estándar con puntajes z.

1. 1
Distribuciones de
probabilidad normal

2. 2
§ 5.1
Introducción a las
distribuciones normales y la
distribución estándar

3. 3
Propiedades de las Distribuciones Normales
Una variable aleatoria continua tiene un número infinito de valores posibles que se
pueden representar mediante un intervalo en la recta numérica.
Horas dedicadas al estudio en un
día.
0 6
3 9 15
12 18 24
21
El tiempo dedicado al
estudio puede ser
cualquier número entre
0 y 24.
La distribución de probabilidad de una variable aleatoria continua se denomina
distribución de probabilidad continua.

4. 4
Propiedades de las Distribuciones Normales
La distribución de probabilidad más importante en estadística es la distribución
normal.
Una distribución normal es una distribución de probabilidad continua para una
variable aleatoria, x. La gráfica de una distribución normal se llama curva normal.
Normal curve
x

5. 5
Propiedades de las Distribuciones Normales
Propiedades de las Distribuciones Normales
1. La media, la mediana y la moda son iguales.
2. La curva normal tiene forma de campana y es simétrica
con respecto a la media.
3. El área total bajo la curva es igual a uno.
4. La curva normal se aproxima, pero nunca toca el eje x a
medida que se aleja cada vez más de la media.
5. Entre μ σ y μ + σ (en el centro de la curva), el gráfico
se curva hacia abajo. El gráfico se curva hacia arriba a
la izquierda de μ σ ya la derecha de μ + σ. Los puntos
en los que la curva pasa de curvarse hacia arriba a
curvarse hacia abajo se denominan puntos de inflexión.

6. 6
Propiedades de las Distribuciones Normales
μ  3σ μ + σ
μ  2σ μ  σ μ μ + 2σ μ + 3σ
Puntos de inflexión
Área total = 1
Si x es una variable aleatoria continua que tiene una distribución normal con media μ
y desviación estándar σ, puede graficar una curva normal con la ecuación:
2 2
( ) 2
1
=
2
x μ σ
y e
σ π
- -
. = 2.178 = 3.14
e π
x

7. 7
Medias y Desviaciones Estándar
Una distribución normal puede tener cualquier media y
cualquier desviación estándar positiva.
Media: μ = 3.5
Standard
deviation: σ  1.3
Media: μ = 6
Desviación
estándar: σ  1.9
La media da la
ubicación de la
línea de simetría.
La desviación estándar describe la dispersión de los datos.
Puntos de
inflexión
Puntos de
inflexión
3 6
1 5
4
2
x
3 6
1 5
4
2 9
7 11
10
8
x

8. 8
Medias y Desviaciones Estándar
Ejemplo:
1. ¿Qué curva tiene la mayor media?
2. ¿Qué curva tiene la mayor desviación estándar?
El eje de simetría de la curva A ocurre en x = 5. El eje de simetría de la curva B
ocurre en x = 9. La curva B tiene la media mayor.
La curva B está más dispersa que la curva A, por lo que la curva B tiene la mayor
desviación estándar.
3
1 5 9
7 11 13
A
B
x

9. 9
Interpretación de gráficos
Ejemplo:
Las alturas de los arbustos de magnolia completamente
desarrollados se distribuyen normalmente. La curva
representa la distribución. ¿Cuál es la altura media de un
arbusto de magnolia completamente desarrollado? Estime
la desviación estándar.
Las alturas de los arbustos de magnolias se distribuyen normalmente con una altura
media de unos 8 pies y una desviación estándar de unos 0,7 pies.
μ = 8
Los puntos de inflexión están a una
desviación estándar de la media.
σ  0.7
6 8
7 9 10
Height (in feet)
x

10. 10
3 1
2 1 0 2 3
z
La distribución normal estándar
La distribución normal estándar es una distribución
normal con una media de 0 y una desviación estándar de 1.
Cualquier valor se puede transformar en un puntaje z usando la fórmula
La escala horizontal
corresponde a las
puntuaciones z.
- -
Value Mean
= = .
Standard deviation
x μ
z
σ

11. 11
La distribución normal estándar
Si cada valor de datos de una variable aleatoria
normalmente distribuida x se transforma en una
puntuación z, el resultado será la distribución normal
estándar.
Después de usar la fórmula para transformar un valor x en un puntaje z, se usa la
Tabla normal estándar en el Apéndice B para encontrar el área acumulada bajo la
curva.
El área que cae en el intervalo bajo la curva
normal no estándar (los valores x) es la misma
que el área bajo la curva normal estándar
(dentro de los límites z correspondientes).
3 1
2 1 0 2 3
z

12. 12
La tabla normal estándar
Propiedades de la Distribución Normal Estándar
1. El área acumulada es cercana a 0 para puntuaciones z cercanas a
z = -3.49.
2. El área acumulada aumenta a medida que aumentan las
puntuaciones z.
3. El área acumulada para z = 0 es 0,5000.
4. El área acumulada es cercana a 1 para puntuaciones z cercanas a
z = 3,49
z = 3.49
Área está cerca a 0.
z = 0
Área is 0.5000.
z = 3.49
Área está cerca a 1.
z
3 1
2 1 0 2 3

13. 13
La tabla normal estándar
Ejemplo:
Encuentre el área acumulada que corresponde a un
puntaje z de 2.71.
z .00 .01 .02 .03 .04 .05 .06 .07 .08 .09
0.0 .5000 .5040 .5080 .5120 .5160 .5199 .5239 .5279 .5319 .5359
0.1 .5398 .5438 .5478 .5517 .5557 .5596 .5636 .5675 .5714 .5753
0.2 .5793 .5832 .5871 .5910 .5948 .5987 .6026 .6064 .6103 .6141
2.6 .9953 .9955 .9956 .9957 .9959 .9960 .9961 .9962 .9963 .9964
2.7 .9965 .9966 .9967 .9968 .9969 .9970 .9971 .9972 .9973 .9974
2.8 .9974 .9975 .9976 .9977 .9977 .9978 .9979 .9979 .9980 .9981
Encuentre el área encontrando 2.7 en la columna de la
izquierda y luego moviéndose a través de la fila hasta la
columna debajo de 0.01.
El área a la izquierda de z = 2,71 es 0,9966.
La Tabla Normal Estándar

14. 14
La tabla normal estándar
Ejemplo:
Encuentre el área acumulada que corresponde a un
puntaje z de -0.25.
z .09 .08 .07 .06 .05 .04 .03 .02 .01 .00
3.4 .0002 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003
3.3 .0003 .0004 .0004 .0004 .0004 .0004 .0004 .0005 .0005 .0005
Encuentre el área encontrando 0.2 en la columna de la
izquierda y luego moviéndose a través de la fila hasta la
columna debajo de 0.05.
El área a la izquierda de z = -0.25 es 0.4013
0.3 .3483 .3520 .3557 .3594 .3632 .3669 .3707 .3745 .3783 .3821
0.2 .3859 .3897 .3936 .3974 .4013 .4052 .4090 .4129 .4168 .4207
0.1 .4247 .4286 .4325 .4364 .4404 .4443 .4483 .4522 .4562 .4602
0.0 .4641 .4681 .4724 .4761 .4801 .4840 .4880 .4920 .4960 .5000
Appendix B: Standard Normal Table

15. 15
Pautas para encontrar áreas
Hallar áreas bajo la curva normal estándar
1. Dibuje la curva normal estándar y sombree el área
apropiada debajo de la curva.
2. Encuentra el área siguiendo las instrucciones para
cada caso que se muestra.
a. Para encontrar el área a la izquierda de z,
encuentre el área que corresponde a z en la tabla
normal estándar.
1. Use la tabla para hallar el
área de la puntuación z.
2. El área a la
izquierda de z =
1.23 es 0.8907.
1.23
0
z

16. 16
Pautas para encontrar área
Hallar áreas bajo la curva normal estándar
b. Para encontrar el área a la derecha de z, use la
tabla normal estándar para encontrar el área que
corresponde a z. Luego resta el área de 1.
3. Resta para encontrar el área
a la derecha de z = 1.23:
1  0.8907 = 0.1093.
1. Usa la tabla para encontrar
el área para el puntaje z.
2. El área a la
izquierda de z =
1.23 es 0.8907.
1.23
0
z

17. 17
Hallar áreas bajo la curva normal estándar
c. Para encontrar el área entre dos puntajes z,
encuentre el área correspondiente a cada puntaje z
en la tabla normal estándar. Luego resta el área
más pequeña del área más grande.
Pautas para encontrar áreas
4. Reste para encontrar el área
de la región entre las dos
puntuaciones z: 0.8907 
0.2266 = 0.6641.
1. Usa la tabla para encontrar el área
para el puntaje z.
3. El área a la
izquierda de z =
0.75 es 0.2266.
2. El área a la
izquierda de z =
1.23 es 0.8907.
1.23
0
z
0.75

18. 18
Pautas para encontrar áreas
Ejemplo:
Encuentre el área bajo la curva normal
estándar a la izquierda de z = -2.33.
De la Tabla Normal Estándar, el área es igual a 0.0099.
¡Dibuje siempre la
curva!
2.33 0
z

19. 19
Pautas para encontrar áreas
Ejemplo:
Encuentre el área bajo la curva normal
estándar a la derecha de z = 0.94.
De la Tabla Normal Estándar, el área es igual a 0.1736.
Dibuje siempre la curva!
0.8264
1  0.8264 = 0.1736
0.94
0
z

20. 20
Pautas para encontrar áreas
Ejemplo:
Encuentre el área bajo la curva normal
estándar entre z = -1.98 y z = 1.07.
De la Tabla Normal Estándar, el área es igual a 0.8338.
¡Dibuje siempre la
curva!
0.8577  0.0239 = 0.8338
0.8577
0.0239
1.07
0
z
1.98

21. 21
§ 5.2
Distribuciones normales:
encontrar probabilidades

22. 22
Probabilidad y Distribuciones Normales
Si una variable aleatoria, x, tiene una distribución
normal, puede encontrar la probabilidad de que x caiga
en un intervalo determinado calculando el área bajo la
curva normal para ese intervalo.
P(x < 15)
μ = 10
σ = 5
15
μ =10
x

23. 23
Probabilidad y Distribuciones Normales
Misma area
P(x < 15) = P(z < 1) = Área sombreada bajo la curva
= 0.8413
15
μ =10
P(x < 15)
μ = 10
σ = 5
Distribución normal
x
1
μ =0
μ = 0
σ = 1
Distribución normal estándar
z
P(z < 1)

24. 24
Ejemplo:
El promedio en una prueba de estadística fue de 78 con una
desviación estándar de 8. Si los puntajes de la prueba se distribuyen
normalmente, encuentre la probabilidad de que un estudiante
obtenga una calificación de menos de 90.
Probabilidad y Distribuciones Normales
P(x < 90) = P(z < 1.5) = 0.9332
-

90-78
=
8
x μ
z
σ
= 1.5
La probabilidad de que un
estudiante obtenga una
calificación de prueba
inferior a 90 es 0.9332.
μ =0
z
?
1.5
90
μ =78
P(x < 90)
μ = 78
σ = 8
x

25. 25
Ejemplo:
El promedio en un examen de estadística fue 78 con una desviación
estándar de 8. Si los puntajes del examen se distribuyen
normalmente, encuentre la probabilidad de que un estudiante
obtenga un puntaje mayor a 85.
Probabilidad y Distribuciones Normales
P(x > 85) = P(z > 0.88) = 1  P(z < 0.88) = 1  0.8106 = 0.1894
85-78
= =
8
x - μ
z
σ

= 0.875 0.88
La probabilidad de que un
estudiante obtenga una
puntuación de examen
superior a 85 es 0.1894.
μ =0
z
?
0.88
85
μ =78
P(x > 85)
μ = 78
σ = 8
x

26. 26
Ejemplo:
El promedio en un examen de estadística fue 78 con una desviación
estándar de 8. Si los puntajes del examen se distribuyen
normalmente, encuentre la probabilidad de que un estudiante
obtenga un puntaje entre 60 y 80.
Probabilidad y Distribuciones Normales
P(60 < x < 80) = P(2.25 < z < 0.25) = P(z < 0.25)  P(z < 2.25)
- -
1
60 78
= =
8
x μ
z
σ
-
= 2.25
La probabilidad de que un
estudiante obtenga un
puntaje de prueba entre 60 y
80 es 0.5865.
2
- -

80 78
=
8
x μ
z
σ
= 0.25
μ =0
z
?
? 0.25
2.25
= 0.5987  0.0122 = 0.5865
60 80
μ =78
P(60 < x < 80)
μ = 78
σ = 8
x

27. 27
§ 5.3
Distribuciones normales:
encontrando los valores

28. 28
Encontrando el puntaje z
Ejemplo:
Encuentre el puntaje z que corresponde a un área acumulada de
0.9973.
z .00 .01 .02 .03 .04 .05 .06 .07 .08 .09
0.0 .5000 .5040 .5080 .5120 .5160 .5199 .5239 .5279 .5319 .5359
0.1 .5398 .5438 .5478 .5517 .5557 .5596 .5636 .5675 .5714 .5753
0.2 .5793 .5832 .5871 .5910 .5948 .5987 .6026 .6064 .6103 .6141
2.6 .9953 .9955 .9956 .9957 .9959 .9960 .9961 .9962 .9963 .9964
2.7 .9965 .9966 .9967 .9968 .9969 .9970 .9971 .9972 .9973 .9974
2.8 .9974 .9975 .9976 .9977 .9977 .9978 .9979 .9979 .9980 .9981
Encuentre el puntaje z ubicando 0.9973 en el cuerpo de la Tabla
Normal Estándar. Los valores al comienzo de la fila correspondiente y
en la parte superior de la columna dan la puntuación z.
El puntaje z es 2.78.
Appendix B: Standard Normal Table
2.7
.08

29. 29
Encontrando el puntaje z
Ejemplo:
Encuentre el puntaje z que corresponde a un área
acumulada de 0.4170.
z .09 .08 .07 .06 .05 .04 .03 .02 .01 .00
3.4 .0002 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003
0.2 .0003 .0004 .0004 .0004 .0004 .0004 .0004 .0005 .0005 .0005
Encuentre el puntaje z ubicando 0.4170 en el cuerpo de la
Tabla Normal Estándar. Utilice el valor más cercano a 0,4170.
0.3 .3483 .3520 .3557 .3594 .3632 .3669 .3707 .3745 .3783 .3821
0.2 .3859 .3897 .3936 .3974 .4013 .4052 .4090 .4129 .4168 .4207
0.1 .4247 .4286 .4325 .4364 .4404 .4443 .4483 .4522 .4562 .4602
0.0 .4641 .4681 .4724 .4761 .4801 .4840 .4880 .4920 .4960 .5000
Appendix B: Standard Normal Table
Utilice el
área más
cercana.
El puntaje z es 0.21.
0.2
.01

30. 30
Encontrar un puntaje z dado un percentil
Ejemplo:
Encontrar un puntaje z que corresponde al percentil
P75.
El puntaje z que corresponde a P75 es el mismo puntaje z que
corresponde a un área de 0.75.
El puntaje z es 0.67.
?
μ =0
z
0.67
Area = 0.75

31. 31
Transformar un puntaje z en un puntaje x
Para transformar un puntaje z estándar en un valor
de datos, x, en una población dada, use la formula:
Ejemplo:
Las facturas mensuales de electricidad en una ciudad se distribuyen
normalmente con una media de $120 y una desviación estándar de
$16. Encuentre el valor de x correspondiente a un puntaje z de 1.60.

x μ+ zσ.

x μ+ zσ
= 120 +1.60(16)
= 145.6
Podemos concluir que una factura de electricidad de $145.60
está 1.6 desviaciones estándar por encima de la media.

32. 32
Encontrar un valor de datos específico
Ejemplo:
Los pesos de las bolsas de papitas para una máquina expendedora se
distribuyen normalmente con una media de 1.25 onzas y una desviación
estándar de 0.1 onzas. Las bolsas que tienen un peso inferior al 8% son
demasiado livianas y no funcionarán en la máquina. ¿Cuánto es lo mínimo
que puede pesar una bolsa de papas fritas y seguir funcionando en la
máquina?

x μ+ zσ
Lo mínimo que una bolsa puede pesar y seguir funcionando en la
máquina es de 1.11 onzas.
? 0
z
8%
P(z < ?) = 0.08
P(z < 1.41) = 0.08
1.41
1.25
x
?
1.25 ( 1.41)0.1
  
 1.11
1.11

33. 33
§ 5.4
Distribuciones de muestreo
y el teorema del límite
central

34. 34
Población
Muestra
Distribuciones de muestreo
Una distribución de muestreo es la distribución de probabilidad de una muestra
estadística que se forma cuando se toman repetidamente muestras de tamaño n de una
población.
Muestra
Muestra
Muestra
Muestra
Muestra
Muestra
Muestra
Muestra
Muestra

35. 35
Distribuciones de muestreo
Si la estadística muestral es la media muestral, entonces la distribución es la distribución
muestral de las medias muestrales.
Muestra 1
1
x
Muestra 4
4
x
Muestra 3
3
x Muestra 6
6
x
La distribución muestral consta de los valores de las medias muestrales,
1 2 3 4 5 6
, , , , , .
x x x x x x
Muestra 2
2
x
Muestra 5
5
x

36. 36
Propiedades de las distribuciones muestrales
Propiedades de las distribuciones muestrales de las medias
muestrales
1. La media de las medias muestrales, es igual a la media
poblacional.
2. La desviación estándar de las medias muestrales, es igual a
la desviación estándar de la población, dividido por la raíz
cuadrada de n.
La desviación estándar de la distribución muestral de las medias
muestrales se llama Error estandar de la media.
,
x
μ
x
μ = μ
,
x
σ
,
σ
x
σ
σ =
n

37. 37
Distribución muestral de las medias muestrales
Ejemplo:
Los valores de población {5, 10, 15, 20} se escriben en tiras de
papel y se colocan en un sombrero. Se seleccionan al azar dos
papeletas, con reemplazo.
a. Encuentre la media, la desviación estándar y la
varianza de la población.
Continuación.
= 12.5
μ
= 5.59
σ
2
= 31.25
σ
Población
5
10
15
20

38. 38
Distribución muestral de las medias muestrales
Continuando con el Ejemplo:
Los valores de población {5, 10, 15, 20} se escriben en tiras de
papel y se colocan en un sombrero. Se seleccionan al azar dos
papeletas, con reemplazo.
b. Grafique el histograma de probabilidad para los
valores de la población.
Continuación.
Esta distribución uniforme
muestra que todos los valores
tienen la misma probabilidad
de ser seleccionados.
Valores de población
Probabilidad
0.25
5 10 15 20
x
P(x) Histograma de probabilidad
de población de x

39. 39
Distribución muestral de las medias muestrales
Continuación del ejemplo:
Los valores de población {5, 10, 15, 20} se escriben en tiras de
papel y se colocan en un sombrero. Se seleccionan al azar dos
papeletas, con reemplazo.
c. Liste todas las muestras posibles de tamaño n = 2 y
calcule la media de cada una.
15
10, 20
12.5
10, 15
10
10, 10
7.5
10, 5
12.5
5, 20
10
5, 15
7.5
5, 10
5
5, 5
Muestra promedio,
Muestra x
20
20, 20
17.5
20, 15
15
20, 10
12.5
20, 5
17.5
15, 20
15
15, 15
12.5
15, 10
10
15, 5
Muestra promedio,
Muestra x
Continuación.
Estas medias
forman la
distribución
muestral de las
medias
muestrales.

40. 40
Distribución muestral de las medias muestrales
Continuación del ejemplo:
Los valores de población {5, 10, 15, 20} se escriben en tiras de
papel y se colocan en un sombrero. Se seleccionan al azar dos
papeletas, con reemplazo.
d. Cree la distribución de probabilidad de las medias
muestrales.
Distribución de
probabilidad de las medias
muestrales
0.0625
1
20
0.1250
2
17.5
0.1875
3
15
0.2500
4
12.5
0.1875
3
10
0.1250
2
7.5
0.0625
1
5
x f Probabilidad

41. 41
Distribución muestral de las medias muestrales
Continuación del ejemplo:
Los valores de población {5, 10, 15, 20} se escriben en tiras de
papel y se colocan en un sombrero. Se seleccionan al azar dos
papeletas, con reemplazo.
e. Grafique el histograma de probabilidad para la
distribución de muestreo.
La forma del gráfico es
simétrica y en forma de
campana. Se aproxima a una
distribución normal.
Muestra promedio
Probabilidad
0.25
P(x) Histograma de probabilidad de
distribución de muestreo
0.20
0.15
0.10
0.05
17.5 20
15
12.5
10
7.5
5
x

42. 42
la muestra media tendrá una distribución normal.
El Teorema del Límite Central
Si se toma una muestra de tamaño n  30 de una pobalación con cualquier tipo de
distribución con una media =  y una desviación estándar = ,
x

x


x
x
x
x
x
x
x
x x
x
x
x x

43. 43
El Teorema del Límite Central
Si la población en sí tiene una distribución normal, con una media =  y una
desviación estándar = ,
las medias muestrales tendrán una distribución normal para cualquier tamaño
de muestra n.

x

x
x
x
x
x
x
x
x x
x
x
x x

44. 44
El Teorema del Límite Central
En cualquier caso, la distribución muestral de las medias muestrales tiene una media igual
a la media poblacional.

x
μ μ

x
σ
σ
n
Media de las
medias muestrales
Desviación estándar de las
medias muestrales
La distribución muestral de las medias muestrales tiene una desviación estándar igual a la
desviación estándar de la población dividida por la raíz cuadrada de n.
Esto también se llama el Error
estandar de la media.

45. 45
La Media y el Error Estándar
Ejemplo:
Las alturas de los arbustos de magnolia completamente desarrollados tienen una altura
media de 8 pies y una desviación estándar de 0.7 pies. Se seleccionan al azar 38
arbustos de la población y se determina la media de cada muestra. Encuentre la media y
el error estándar de la media de la distribución muestral.

x
μ μ
Media
Desviación estándar (error estándar)

x
σ
σ
n
= 8
0.7
=
38
= 0.11
Continuación.

46. 46
Interpretación del Teorema del Límite Central
Continuación del ejemplo:
Las alturas de los arbustos de magnolia completamente desarrollados tienen una
altura media de 8 pies y una desviación estándar de 0.7 pies. Se seleccionan al azar
38 arbustos de la población y se determina la media de cada muestra.
A partir del teorema del límite central, dado que el
tamaño de la muestra es mayor que 30, la
distribución muestral puede aproximarse mediante
la distribución normal.
La media de la distribución de muestreo es de 8 pies y el error estándar de la
distribución de muestreo es de 0.11 pies.
x
8 8.4
7.6
= 8
x
μ = 0.11
x
σ

47. 47
Encontrando Probabilidades
Ejemplo:
Las alturas de los arbustos de magnolia completamente desarrollados tienen una
altura media de 8 pies y una desviación estándar de 0.7 pies. Se seleccionan al azar
38 arbustos de la población y se determina la media de cada muestra.
Calcule la probabilidad de que la altura media de
los 38 arbustos sea inferior a 7,8 pies.
La media de la distribución de muestreo es de 8 pies y el
error estándar de la distribución de muestreo es de 0.11
pies.
7.8
x
8.4
7.6 8
Continuación.
= 8
x
μ
= 0.11
x
σ
= 38
n

48. 48
P ( < 7.8) = P (z < ____ ) ?
x 1.82
Encontrando Probabilidades
Continuación del ejemplo:
Calcula la probabilidad de que la altura media de los 38 arbustos sea inferior a 7.8
pies.

 x
x
x μ
z
σ

7.8 8
=
0.11
7.8
x
8.4
7.6 8
= 8
x
μ
= 0.11
x
σ
n = 38

= 1.82
z
0
La probabilidad de que la altura media de los 38 arbustos sea inferior a 7.8 pies es
0.0344.
= 0.0344
P ( < 7.8)
x

49. 49
Ejemplo:
El promedio en un examen de estadística fue 78 con una desviación
estándar de 8. Si los puntajes del examen se distribuyen
normalmente, encuentre la probabilidad de que el puntaje promedio
de 25 estudiantes seleccionados al azar esté entre 75 y 79.
Probabilidad y Distribuciones Normales
 
x
x
x μ
z
σ
1
75 78
= =
1.6

= 1.88
 
x μ
z
σ
2
79 78
= =
1.6
= 0.63
0
z
?
? 0.63
1.88
= 78
σ 8
= = = 1.6
n 25
x
x
μ
σ
Continuación.
P (75 < < 79)
x
75 79
78
x

50. 50
Continuación del Ejemplo:
Probabilidad y Distribuciones Normales
Aproximadamente el 70,56% de los 25 alumnos tendrán una puntuación media entre 75 y
79.
= 0.7357  0.0301 = 0.7056
0
z
?
? 0.63
1.88
P (75 < < 79)
x
P(75 < < 79) = P(1.88 < z < 0.63) = P(z < 0.63)  P(z < 1.88)
x
75 79
78
x

51. 51
Ejemplo:
El salario medio poblacional de los mecánicos de automóviles es  =
$34,000 con una desviación estándar de  = $2,500. Encuentre la
probabilidad de que el salario medio de una muestra seleccionada al azar
de 50 mecánicos sea mayor que $35,000.
Probabilidades de x y x
 
 x
x
x μ
z
σ
35000 34000
=
353.55
= 2.83
0
z
?
2.83

= 34000
2500
= = 353.55
50
x
x
μ
σ
σ
n
= P (z > 2.83) = 1  P (z < 2.83)
= 1  0.9977 = 0.0023
La probabilidad de que el salario
medio de una muestra seleccionada
al azar de 50 mecánicos sea mayor
que $35,000 es 0.0023.
35000
34000
P ( > 35000)
x
x

52. 52
Ejemplo:
El salario medio poblacional de los mecánicos de
automóviles es  = $34,000 con una desviación estándar de
 = $2,500. Encuentre la probabilidad de que el salario de
un mecánico seleccionado al azar sea mayor a $35,000.
Probabilidades de x y x
- 35000-34000
= =
2500
x μ
z
σ
= 0.4
0
z
?
0.4
= 34000
= 2500
μ
σ
= P (z > 0.4) = 1  P (z < 0.4)
= 1  0.6554 = 0.3446
La probabilidad de que el salario de
un mecánico sea mayor a $35,000
es 0.3446.
(Observe que el Teorema del Límite Central no se aplica).
35000
34000
P (x > 35000)
x

53. 53
Ejemplo:
La probabilidad de que el salario de un mecánico
seleccionado al azar sea mayor a $35,000 es 0.3446. En un
grupo de 50 mecánicos, aproximadamente ¿cuántos
tendrían un salario mayor a $35,000?
Probabilidades de x y x
P(x > 35000) = 0.3446
Esto también significa que el 34,46% de los
mecánicos tienen un salario superior a
$35,000.
Se esperaría que unos 17 mecánicos del grupo de 50 tuvieran un salario superior a
$35,000.
34.46% of 50 = 0.3446  50 = 17.23

54. 54
§ 5.5
Aproximaciones Normales a
Distribuciones Binomiales

55. 55
Aproximación Normal
La distribución normal se usa para aproximar la distribución
binomial cuando no sería práctico usar la distribución
binomial para encontrar una probabilidad.
Aproximación Normal a una Distribución Binomial
Si np  5 y nq  5, entonces la variable aleatoria binomial
x tiene una distribución aproximadamente normal con
media
y desviación estándar

σ npq.

μ np

56. 56
Aproximación Normal
Ejemplo:
Decida si es possible utilizar la distribución normal para aproximar x
en los siguientes ejemplos.
1. Treinta y seis por ciento de las personas en los Estados Unidos
tienen un perro. Selecciona al azar a 25 personas en los
Estados Unidos y les pregunta si tienen un perro.
2. El catorce por ciento de las personas en los Estados Unidos
tienen un gato. Selecciona al azar a 20 personas en los Estados
Unidos y les pregunta si tienen un gato.
= (25)(0.36) = 9
np
= (25)(0.64) = 16
nq
Como np y nq son mayores que 5, se puede
usar la distribución normal.
= (20)(0.14) = 2.8
np
= (20)(0.86) = 17.2
nq
Debido a que np no es mayor que 5, NO se
puede usar la distribución normal.

57. 57
Corrección por Continuidad
La distribución binomial es discreta y se puede representar mediante un histograma de
probabilidad.
A esto se le llama corrección por continuidad.
Cuando utilice la distribución normal continua para aproximar una distribución
binomial, muévase 0.5 unidades hacia la izquierda y hacia la derecha del punto
medio para incluir todos los valores x posibles en el intervalo.
Para calcular las probabilidades binomiales
exactas, se utiliza la fórmula binomial para
cada valor de x y se suman los resultados.
Probabilidad binomial exacta
c
x
P(x = c)
P(c 0.5 < x < c + 0.5)
Aproximación
normal
c
x
c + 0.5
c  0.5

58. 58
Corrección por Continuidad
Ejemplo:
Utilice una corrección por continuidad para convertir los intervalos
binomiales en un intervalo de distribución normal.
1. La probabilidad de obtener entre 125 y 145 aciertos, inclusive.
Los valores discretos del punto medio son 125, 126, …, 145.
El intervalo continuo es 124.5 < x < 145.5.
2. La probabilidad de obtener exactamente 100 éxitos.
El valor discreto del punto medio es 100.
El intervalo continuo es 99.5 < x < 100.5.
3. The probability of getting at least 67 successes.
Los valores discretos del punto medio son 67, 68, ….
El intervalo continuo es x > 66.5.

59. 59
Lineamientos
Uso de la Distribución Normal para Aproximar Probabilidades Binomiales
En Palabras En Símbolos
1. Verifique que aplica la distribución binomial.
2. Determina si puedes usar la distribución normal
para aproximar x, la variable binomial.
3. Encuentre la media  y la desviación estándar 
para la distribución.
4. Aplique la corrección de continuidad adecuada.
Sombrea el área correspondiente bajo
la curva normal.
5. Encuentre los valores z correspondientes.
6. Encuentra la probabilidad.

σ npq
-

x μ
z
σ
Especificar n, p, y q.
¿Es np  5?
¿Es nq  5?

μ np
Sume o reste 0,5 de
los puntos finales.
Utilice la tabla
normal estándar.

60. 60
Aproximación de una Probabilidad Binomial
Ejemplo:
Treinta y uno por ciento de los estudiantes de último año en cierta escuela
secundaria planean asistir a la universidad. Si se seleccionan 50 estudiantes al
azar, encuentre la probabilidad de que menos de 14 estudiantes planeen asistir
a la universidad.
np = (50)(0.31) = 15.5
nq = (50)(0.69) = 34.5
La variable x tiene aproximadamente una
distribución normal con  = np = 15.5 y
= (50)(0.31)(0.69) = 3.27.
σ = npq
P(x < 13.5)
Corrección por continuidad
- -
-

13.5 15.5
= = 0.61
3.27
x μ
z
σ
= P(z < 0.61)
10 15
x
20
= 15.5
13.5
= 0.2709
La probabilidad de que menos de 14 planeen asistir a la universidad es 0.2079.

61. 61
Aproximación de una Probabilidad Binomial
Ejemplo:
Una encuesta informa que el cuarenta y ocho por ciento de los
ciudadanos estadounidenses poseen computadoras. Se seleccionan al
azar 45 ciudadanos y se les pregunta si tiene computadora. ¿Cuál es la
probabilidad de que exactamente 10 digan que sí?
np = (45)(0.48) = 12
nq = (45)(0.52) = 23.4  = (45)(0.48)(0.52) = 3.35
σ npq
P(9.5 < x < 10.5)
Corrección por continuidad
5 10
x
15
 = 12
9.5
= 0.0997
La probabilidad de que exactamente 10 ciudadanos
estadounidenses tengan una computadora es 0.0997.
= 12
μ
10.5
= P(0.75 < z  0.45)