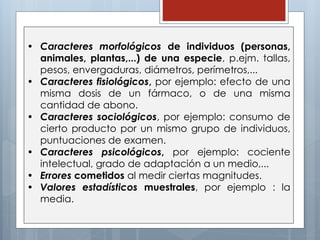
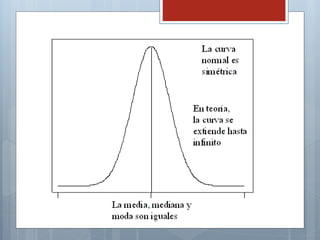
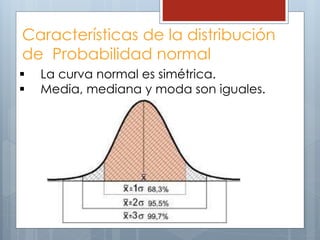
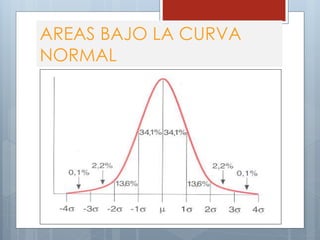
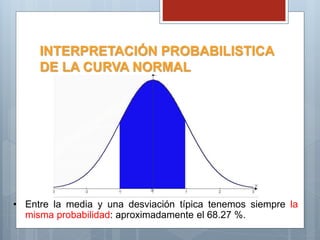
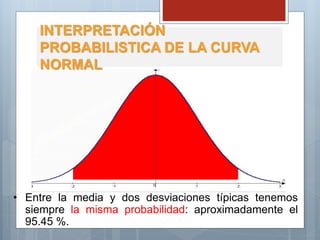
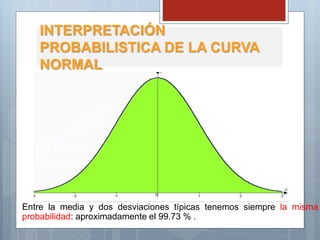
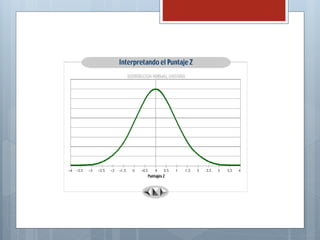
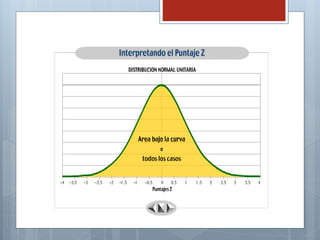
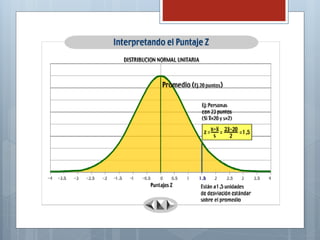
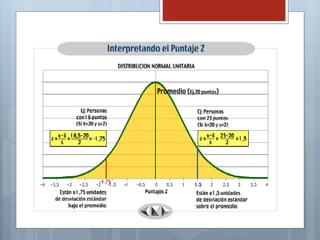
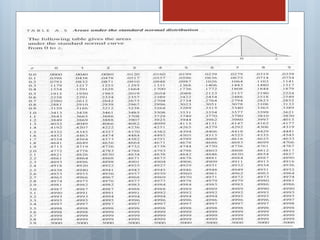
El documento describe las características principales de la distribución normal de probabilidad. La distribución normal es simétrica con respecto a su media, y la curva decrece uniformemente en ambas direcciones desde el valor central. Es una de las distribuciones continuas más importantes debido a que muchas variables asociadas a fenómenos naturales siguen este patrón.