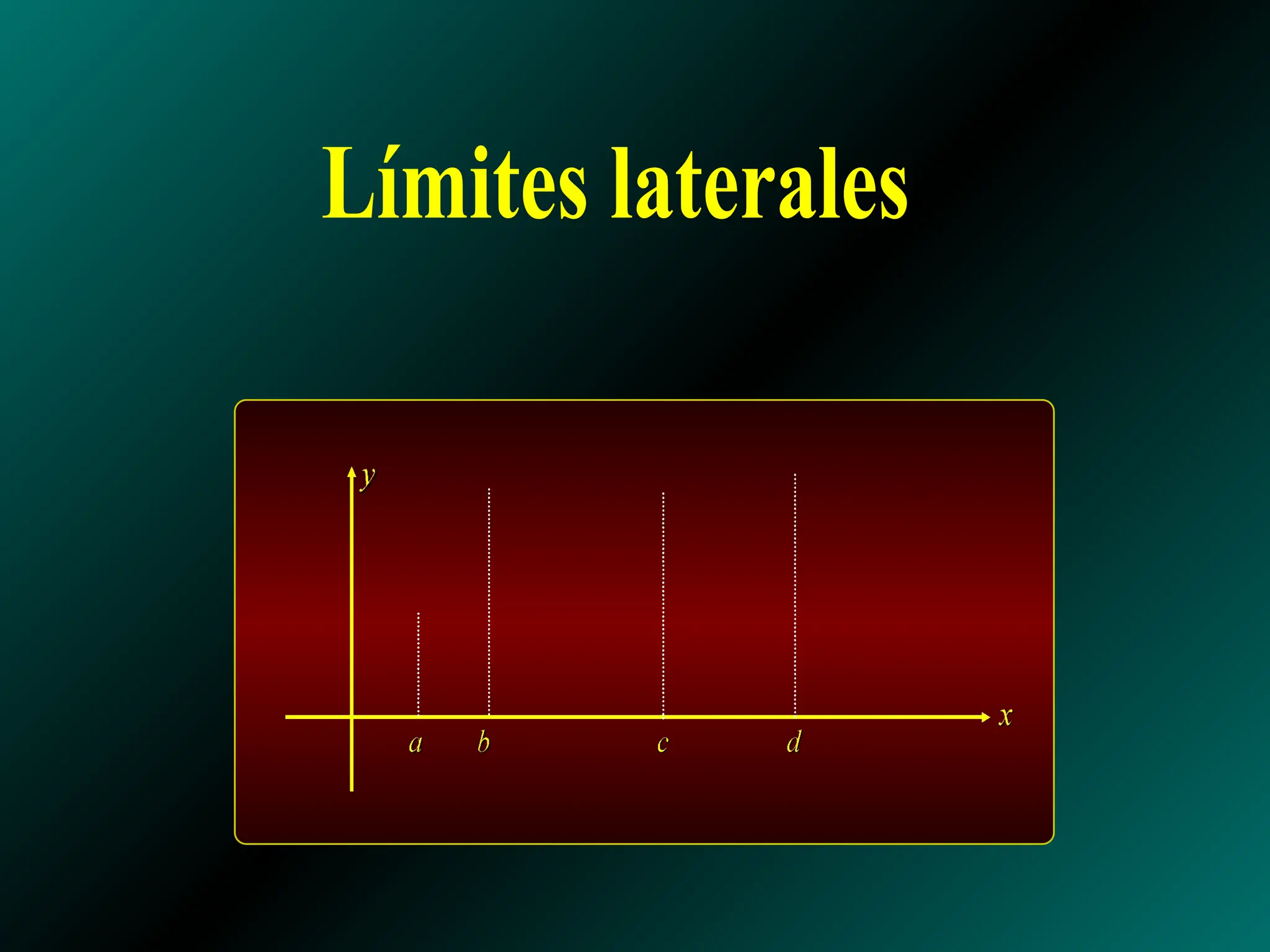
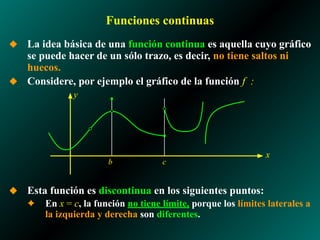
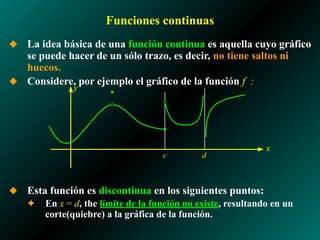
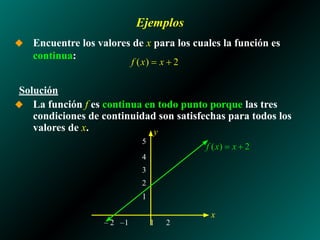
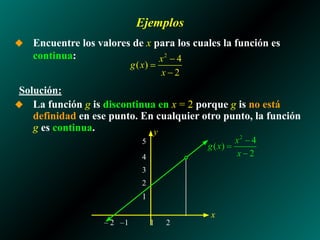
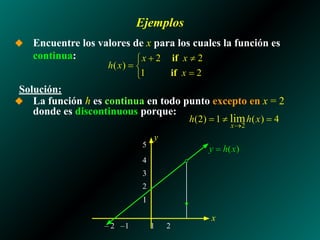
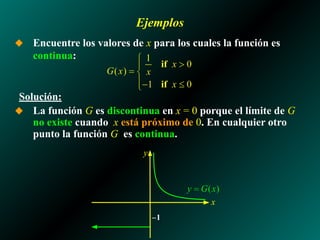
El documento analiza los límites laterales de funciones y su relación con la continuidad, indicando que las funciones son continuas si no presentan saltos ni huecos en su gráfico. Se presentan ejemplos de funciones discontinuas en diversos puntos y se establecen propiedades de continuidad para funciones polinómicas y racionales. También se discuten las condiciones necesarias para que una función sea continua en un punto específico y a lo largo de un intervalo.

1. Límites laterales

2. Límites Laterales
◆ Considere la función:
◆ Su gráifco muestra que
f NO TIENE UN
LÍMITE cuando x está
próximo de cero,
porque al aproximanos
a cero por cada lado se
obtienen resultados
diferentes.
1
–1
x
y
–1 1

3. Límites Laterales
◆ Considere la función:
◆ Si restringimos x a tomar
valores mayores que cero (a la
derecha de cero), vemos que f(x)
está muy próximo de 1 cuando
damos valores a x próximos 0.
◆ En este caso, decimos que límite
lateral a la derecha de f cuando
x está próximo de 0 es 1,
denotado por:
1
–1
x
y
–1 1

4. Límites Laterales
◆ Considere la función:
◆ Análogamente, si restringimos a x
a tomar valores menores que cero
(a la izquierda de cero), vemos
que f(x) está muy próximo de –1
cuando x está próximo de 0.
◆ En este caso, decimos que el
límite lateral a la izquierda de f
cuando x está próximo de 0 es – 1,
denotado por:
1
–1
x
y
–1 1

5. Límites Laterales
◆ La función f tiene límite lateral a la derecha L cuando
x se aproxima por la derecha de a, denotado por:
si los valores de f(x) están muy cercanos a L cuando
tomamos valores de x suficientemente cerca a (pero no
igual a) a y a la derecha de a.
◆ Similarmente, la función f tiene Límite lateral a la
izquierda L cuando x se aproxima por la izquierda de
a , denotado por:
si los valores de f(x) se aproximan a L cuando
tomamos valores de x suficientemente cerca a (pero no
igual a) a y a la izquierda de a.

6. Teorema 3
Propiedades de Límites
◆ Sea f una función que está definida para todos los
valores de x cercanos a x = a con la posible excepción
que f también esté definida para x = a . Entonces:
◆ La conexión entre Límites laterales y el concepto de
límite definido anteriormente es dado por el siguiente
teorema:

7. – 2 –1 1 2
Ejemplo
◆ Muestre que existe analizando los límites
laterales de f cuando x está muy próximo de 0:
Solución:
◆ Para x > 0, tenemos:
◆ Y para x ≤ 0, se tiene que:
◆ Por tanto:
2
1
x
y

8. Funciones continuas
◆ La idea básica de una función continua es aquella cuyo gráfico
se puede hacer de un sólo trazo, es decir, no tiene saltos ni
huecos.
◆ Considere, por ejemplo el gráfico de la función f :
◆ Esta función es discontinua en los siguientes puntos:
✦ En x = a, f no está definida (x = a no está en el dominio de f ).
a
x
y

9. Funciones continuas
◆ La idea básica de una función continua es aquella cuyo gráfico
se puede hacer de un sólo trazo, es decir, no tiene saltos ni
huecos.
◆ Considere, por ejemplo el gráfico de la función f :
◆ Esta función es discontinua en los siguientes puntos:
✦ En x = b, f(b) no es igual al límite de de f(x) cuando x está muy
próximo de b.
a
x
y
b

10. Funciones continuas
◆ La idea básica de una función continua es aquella cuyo gráfico
se puede hacer de un sólo trazo, es decir, no tiene saltos ni
huecos.
◆ Considere, por ejemplo el gráfico de la función f :
◆ Esta función es discontinua en los siguientes puntos:
✦ En x = c, la función no tiene límite, porque los límites laterales a
la izquierda y derecha son diferentes.
x
y
b c

11. Funciones continuas
◆ La idea básica de una función continua es aquella cuyo gráfico
se puede hacer de un sólo trazo, es decir, no tiene saltos ni
huecos.
◆ Considere, por ejemplo el gráfico de la función f :
◆ Esta función es discontinua en los siguientes puntos:
✦ En x = d, the límite de la función no existe, resultando en un
corte(quiebre) a la gráfica de la función.
x
y
c d

12. Continuidad de una función en un punto x = a
◆ Una función f es continua en un número x = a
si las siguientes condiciones son satisfechas:
1. f(a) está defineda.
2.
3.
◆ Si f no es continua en x = a, entonces f is
llamada discontinua en x = a.
◆ Además, f es continua sobre un intervalo si
f es continua en todo punto del intervalo.

13. Ejemplos
◆ Encuentre los valores de x para los cuales la función es
continua:
Solución
◆ La función f es continua en todo punto porque las tres
condiciones de continuidad son satisfechas para todos los
valores de x.
– 2 –1 1 2
5
4
3
2
1
x
y

14. Ejemplos
◆ Encuentre los valores de x para los cuales la función es
continua:
Solución:
◆ La función g is discontinua en x = 2 porque g is no está
definidad en ese punto. En cualquier otro punto, la función
g es continua.
– 2 –1 1 2
5
4
3
2
1
x
y

15. Ejemplos
◆ Encuentre los valores de x para los cuales la función es
continua:
Solución:
◆ La función h es continua en todo punto excepto en x = 2
donde es discontinuous porque:
– 2 –1 1 2
5
4
3
2
1
x
y

16. Ejemplos
◆ Encuentre los valores de x para los cuales la función es
continua:
Solución:
◆ La función F is discontinuao en x = 0 porque el límite de F
no existe cuando x se aproxima a 0. En cualquier otro
punto, la función F es continua.
1
–1
x
y

17. Ejemplos
◆ Encuentre los valores de x para los cuales la función es
continua:
Solución:
◆ La función G es discontinua en x = 0 porque el límite de G
no existe cuando x está próximo de 0. En cualquier otro
punto la función G es continua.
–1
x
y

18. Propiedades de las Funciones Continuas
1. La función constante f(x) = c es continua en todo punto.
2. La función identidad f(x) = x es continua en todo punto.
Si f y g are funciones continuas en x = a, entonces:
3. [f(x)]n
, donde n es un número real, es continua en
x = a siempre que esté bien definida en x = a .
4. f ± g es continua en x = a.
5. fg es continua en x = a.
6. f /g es continua si g(a) ≠ 0.

19. Propiedades las funciones continuas.
◆ Usando las propiedades anterioes, se obtienen las
siguientes propiedades:
1. Una función polinomial y = P(x) es continua en todo
valor de x.
2. Una función racional R(x) = p(x)/q(x) es continua en
todo valor de x donde q(x) ≠ 0.

20. Ejemplos
◆ Encuentre los valores de x para los cuales la función es
continua:
Solución:
◆ La función g es una función racional.
◆ Observe que el denominador de g nunca es igual a cero.
◆ Entonces, podemos concluir que g(x) es continua para todo
valor de x.

21. Ejemplos
◆ Encuentre los valores de x para los cuales la función es
continua:
Solución:
◆ La función h es una función racional.
◆ En este caso, observar que el denominador de h es igual a
zero en x = 1 y x = 2, que se obtienen al factorizar el
denominador.
◆ Entonces, podemos concluir que h(x) es continua en todo
punto excepto en x = 1 y x = 2.