1) El documento explica conceptos fundamentales de límites y continuidad en análisis matemático como la aproximación a un punto y la noción de pequeñas variaciones. 2) Define una función continua como aquella cuya gráfica puede dibujarse sin levantar el lápiz y discute límites de funciones simples como polinomios. 3) Presenta teoremas clave sobre límites de funciones como sumas, productos y cocientes así como límites de funciones trascendentes y aparentemente indeterminados.

1. Límite y Continuidad
Integrante:
Andrés Nieves 26.712.194
Marzo 2022

2. Límite y Continuidad
En análisis real y complejo,
el concepto de límite es la
clave de toque que formaliza
la noción intuitiva de
aproximación hacia un punto
concreto de una sucesión o
una función, a medida que
los parámetros de esa
sucesión o función se acercan
a un determinado valor.
Límite Continuidad
una función continua es aquella para la
cual, intuitivamente, para puntos
cercanos del dominio se producen
pequeñas variaciones en los valores de
la función; aunque en rigor, en
un espacio métrico como en variable
real, significa que pequeñas variaciones
de la función implican que deben estar
cercanos los puntos. Si la función no es
continua, se dice que es discontinua.
Informalmente, una función continua
de ℝ en ℝ es aquella cuya gráfica puede
dibujarse sin levantar el lápiz del
papel.

3. Límite de una Función Real
Sea f una función que está definida en un intervalo abierto que contiene al punto a, excepto
posiblemente en el mismo punto a. Diremos que el límite de f(x) cuando x tiende a a es el número
L, y escribiremos.
Lim f(x)=L,
x a
Si cuando x está cerca de a, pero sin llegar a será ,f(x) está cerca de L.
Este número L puede o no existir, pero si existe, éste es único; es decir, toda función tiene, en un
punto dado, a 10 más un limite

4. Ejemplos:
Hallar Lim (x + 3)
x -1
Solución: Cuando x está cerca de -1, x+3 está
cerca de -1 +3 = 2.
Luego,
Lim (x + 3) – 2
x -1
Hallar Lim f(x), donde f(x) =
x
2
+ 1, si x =4
5, si x =
4
Solución:
La f(x) coincide con la función lineal
g(x)= x + 1 en todo R , excepto en x = 4.
Luego,
2
Lim f(x)= Lim g(x)= Lim
x 4 x 4 x 4
x
2
+ 1
=4 +1=2 + 1
2

5. Interpretación Geométrica
Se llama entorno o vecindad de un punto 𝑎 con radio δ en ℝ, al conjunto de valores 𝑥 que se
encuentren dentro del intervalo abierto
El punto 𝑎 es el punto central del intervalo, pero podemos incluirlo o no. Cuando se
excluye, decimos que se trata de un entorno reducido

6. Si este concepto lo llevamos a un espacio bidimensional, por
ejemplo, para 𝑓(𝑥)=−2𝑥2+8𝑥−4 vamos
a determinar el entorno reducido 𝑄′(3 ,1) en el plano cartesiano.
El punto 𝑥=3 es el centro del entorno y nunca será parte del
intervalo. El radio 𝛿 es 1, y lo llamaremos
Δ𝑥=1. En los extremos del intervalo trazamos una línea vertical
hasta que cortemos a la curva.
Se puede reducir
el área de la
región
rectangular hasta
llegar a un radio
infinitamente
pequeño

7. Ejemplos:
f(x) = 2x + 1
lim f(x)=5
x 2+
lim f(x)=5
x 2-
lim f(x)=lim f(x)= lim f(x)= 5
x 2+ x 2- x 2
f(x)= 1
x-2
lim f(x)=
x 2+
lim f(x)=
x 2-
lim f(x)=
x 2+
lim f(x)
x 2-
lim f(x)
x 2

8. Teorema y Límite de Funciones.
Los teoremas se numeran consecutivamente para
facilitar una futura referencia.
Teorema 1:
Límite de una función constante.
Sea f(x)=k (constante), entonces:
Lím f(x) = Lím k = k
x a x a
Teorema 2:
Límite de f(x) = x. Sea f(x)= x. Entonces:
Lim f(x) = Lim x = a
x a x a
Teorema 3:
Límite de una función multiplicada por una constante.
Sea k una constante y f(x) una función dada. Entonces:
Lim k f(x) = k Lim f(x)
x a x a
Teorema 4:
Límite de una potencia. Sea n un entero
positivo, entonces:
Lim x = a
x a
n n

9. Teorema 5:
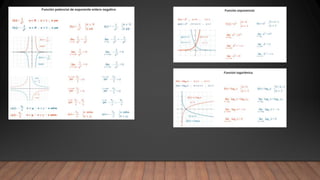
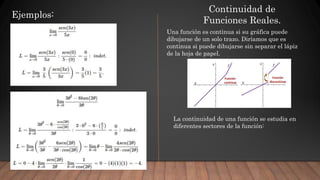
Límite de una suma, diferencia, producto y cociente de
funciones. Supóngase que
Lim F(x) = L1 y Lim G(x) = L2
x a x a
Entonces:
1.Lim[ F(x)+G(x) ] = L1 + L2
x a
2. Lim[ F(x) - G(x) ] = L1 - L2
x a
3. Lim[ F(x) G(x) ] = L1 * L2
x a
4. Lim[ F(x) / G(x) ] = L1 / L2
x a si L2 no es igual a cero
Teorema 6:
Límite de un polinomio. Sea
f(x) una función polinomial,
entonces:
Lim f(x) = f(a)
x a
Teorema 7:
Límite de una función racional.
Sea f(x)=p(x)/q(x) un cociente de
polinomios, entonces:
Lim f(x) = p(a)/q(a)
x a si q(a) no es cero.

10. Ejemplos:
1.De acuerdo con el
teorema de limite 1
Lím 77 =77
x 3
2.f(x)= x +2x-1: función polinomial
f(x)= 2 +2(2)-1= 7;
Por lo tanto, según el teorema 6:
Lim (x +2x-1) = 7.
x 2
2
2
2
Cálculo de límites de funciones
elementales y transcendentales
Función potencial de
exponente natural

12. Los Límites de funciones trascendentes en Calculo
Diferencial para encontrar el Limite de senx.
Tomare como ejemplo clara la función f(x) = senx/x no está
definida en x = 0, pero podemos construir una tabla para
valores próximos a 0. Recuerda que cuando
calculemos senx, la calculadora debe estar en la modalidad
de radianes:
Tal modo que los datos que obtendrás son, para conjeturar podemos
apreciar la gráfica correspondiente. Al apreciar la tabla es fácil darse
cuenta que al evaluar la función directamente en x = 0 queda
perfectamente definido el límite buscado.
Límites Aparentemente
Indeterminados
Los límites indeterminados
(o indeterminaciones) no indican que
el límite no exista, sino que no se
puede anticipar el resultado.
Se tendrán que hacer operaciones
adicionales para eliminar la
indeterminación y averiguar entonces
el valor del límite (en el caso de que
exista). Ese valor puede ser un número
finito, incluido el cero, o +∞ o bien -∞.
Aparecen indeterminaciones cuando, al
sustituir la variable (x) de la expresión
por el valor del límite al que tiende
ésta, se convierte en uno de los casos
siguientes:

13. Pero no serán indeterminaciones cuando, al realizar la
sustitución mencionada de la variable por el valor de su
límite, aparecen resultados como estos, siendo m un
valor finito diferente de cero:
El siguiente límite, por ejemplo, es
indeterminado:
Por el contrario, este límite no tiene indeterminación:
Otro ejemplo seria:
La indeterminación ∞ / ∞ se puede resolver
dividiendo el numerador y el denominador por el
mayor grado de la variable.
Pueden haber tres casos de este tipo de límites
indeterminados:
Que el mayor grado en el numerador sea mayor que
el mayor grado del denominador. En este caso, el
límite es o +∞ o -∞.

14. Límites de Funciones
Trigonométricas
Recordamos que el límite L de cualquier
función y=f(x), las trigonométricas entre
ellas, cuando x tiende a un valor a, es el
valor al que la y o función se acerca (o toma)
cuando la x toma valores muy cerca de a sin
coincidir nunca con ese valor de a.
La función debe estar definida en un intervalo
abierto que contenga a a excepto, posiblemente, en
ese valor a.De acuerdo con la definición de las
funciones seno y coseno, como la ordenada y la
abscisa de un punto P que se mueve en una
circunferencia unitaria en un sistema de ejes
coordenados, determinando el ángulo x en cada
posición; intuitivamente podemos establecer que:
Para todo valor de a en los reales, ya que son
funciones definidas en todos los reales y para un
pequeño cambio en la posición de P se dará un
pequeño cambio en los valores de x (el ángulo), el sen
x (ordenada de P) y el cos x (abscisa de P), y entonces
el valor del límite coincidirá con el de la imagen. Las
funciones seno y coseno son continuas en todo su
dominio que es todos los reales.
Pero lim sen(x)=No existe y lim cos (x)=
x →∞ x →∞
No existe ya que las dos funciones son periódicas,
están variando entre menos uno y uno.

15. Ejemplos:
Continuidad de
Funciones Reales.
Una función es continua si su gráfica puede
dibujarse de un solo trazo. Diríamos que es
continua si puede dibujarse sin separar el lápiz
de la hoja de papel.
La continuidad de una función se estudia en
diferentes sectores de la función:

16. Una función f es continua en un punto x = a
si cumple las tres condiciones siguientes:
En el caso de que en un punto x = a
no se cumpla alguna de las tres
condiciones, se dice que la función es
discontinua en a.
La continuidad lateral de una función f
estudia si ésta es continua en los laterales de
un punto x=a. Por lo tanto, se estudia la
continuidad lateral a izquierda o derecha.
Una función es continua en un intervalo [a,b] si es
continua en todos sus puntos. En caso contrario, se
dice que la función es discontinua en [a,b].

17. Bibliografía
https://www.universoformulas.com/matematicas/analisis/continuidad-
funciones/#:~:text=Una%20funci%C3%B3n%20es%20continua%20si,y%20la%20gr%C3%A1fica%20
se%20rompe.
https://www.docdroid.net/VdQrl1h/jorge-saenz-calculo-pdf#page=109
http://introduccioncalculo.azc.uam.mx/Limite_trigonometrico.html