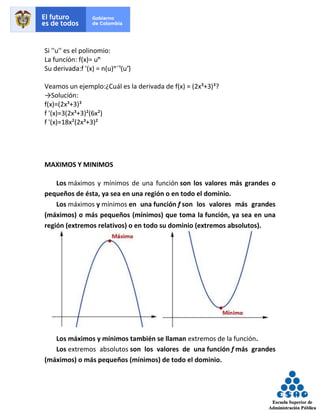
Este documento discute los conceptos de límite y derivada en matemáticas. Explica que un límite representa el valor al que se acerca una función cuando su variable tiende a cierto valor, y que la derivada mide la tasa de cambio de una función en un punto determinado. También presenta ejemplos de cómo calcular límites y derivadas usando diferentes métodos como la factorización o la regla de L'Hôpital.

1. INVESTIGACION
GUITSETH TATIANA ARDILA HERRERA
2 SEMESTRE ARAUQUITA
ESCUELA SUPERIOR DE ADMINISTRACION PUBLICA
2021

2. LIMITE
Un límite es una división, ya sea física o simbólica, que marca
una separación entre dos territorios o naciones. Por ejemplo: “Las
autoridades están furiosas porque afirman que el país vecino ha violado el
límite territorial”, “¿Ves esos árboles? Son el límite de nuestra propiedad, así
que no puedes jugar a la pelota más allá”, “El ecuador es una línea imaginaria
que divide al planeta a la mitad”
En el ámbito de la matemática, por último, un límite es una magnitud fija a la
que se acercan de manera progresiva los términos que conforman una
secuencia infinita de magnitudes.
De esta forma, teniendo en cuenta lo dicho, puede hablarse del límite de una
función, el límite de una sucesión, etc.
En las fórmulas matemáticas, el límite se representa de la siguiente
manera: lim (an) = a. También se puede representar con los siguientes
símbolos: an → a.

3. LIMITE DE UNA FUCION
El vocablo que nos ocupa en primer lugar, límite, podemos decir que se trata
de una palabra que procede, etimológicamente hablando, del latín. En
concreto, emana del sustantivo “limes”, que puede traducirse como
“frontera o borde”. Función, por su parte, también coincide con el término
anterior en lo que respecta a su origen. Y es que, de igual modo, viene del
latín, más exactamente de “functio”, que es sinónimo de “función o
ejecución”.

4. La expresión límite de una función se utiliza en el cálculo diferencial
matemático y refiere a la cercanía entre un valor y un punto. Por ejemplo: si
una función f tiene un límite X en un punto t, quiere decir que el valor
de f puede ser todo lo cercano a X que se desee, con puntos suficientemente
cercanos a t, pero distintos.
Dentro de lo que sería el límite de la función, tendríamos que destacar la
existencia de una teoría muy importante. Nos estamos refiriendo a la teoría
del sándwich, también conocida como teorema del emparedado, que tiene
su origen en tiempos del físico griego Arquímedes, que la usó al igual que
hiciera el matemático Eudoxo de Cnido, que era discípulo del filósofo Platón.
No obstante, se considera que el verdadero formulador de aquella no es otro
que el matemático y astrónomo alemán Carl Friedrich Gauss (1777 – 1855),
que ha pasado a la Historia por el calificativo de “príncipe de las
Matemáticas”.

5. CALCULO DE LIMITES
En el cálculo de límites, hay que tener en primer lugar las propiedades de
los límites.
Tenemos a continuación una tabla con operaciones cuando el cálculo se
efectúa con valores de límites de ∞ o con un número, incluido el 0. Estos
cálculos son sobre el valor del límite, no se trata de operaciones con
números, porque ∞ no lo es. Cuando los signos son evidentes, se omiten. (En
las líneas con dos ±, debe entenderse que o se usa el + en los dos casos o el –
también en ambos).

6. El primer paso para intentar resolver un límite cuando la variable x tiende
al valor a consiste en substituir directamente la variable x por el valor
del límite a. Entonces ver el resultado, sin otra consideración.
Es decir, que en una función de tipo usual, como en una función
continua, y está definida en el entorno del límite a, lo esperable es que
directamente sea:
Como es este caso:
En cambio, no existe este límite:
Y es que la función no está definida en el entorno de -3, porque -3 no
está en el campo de existencia de la función, el cual está restringido al
subconjunto de los reales positivos.
Si en esa substitución se llega a un caso de indeterminación, se tratará
de resolver según el tipo de indeterminación de que se trate.
Una técnica muy potente para resolver
determinadas indeterminación> es la regla de L’Hôpital.
Se disponen de técnicas para resolver límites.
La primera es la factorización.

7. Veamos un ejemplo de resolución por factorización.
La factorización, en el primer caso ha sido por factor común, en el
segundo, por diferencia de cuadrados y en el tercero, hallando las raíces de
un polinomio de segundo grado.
Para calcular el límite de una función con radicales, se multiplica el
término con la raíz por su conjugado (suma por diferencia es igual a la
diferencia de cuadrados).
Veamos este límite (que sería una indeterminación 0/0:
Esta función no está definida en x=2.
Se multiplica el numerador y el denominador por el término conjugado
del que contiene la raíz. Se opera, se simplifica y se substituye la x por el valor
del límite:

8. El valor de este límite es 4/3.
Como se ve en la figura:
Si se da el caso, un cálculo muy eficaz del límite se hará por funciones
equivalentes.
Este es un ejemplo de Cálculo de límites por infinitésimos equivalentes:
Y este un ejemplo de Cálculo de límites por órdenes de infinito:

9. Aplicación de límites en Economía, Administración
Los límites son particularmente importantes en la Economía, la
Administración, y demás ciencias afines, porque nos permiten determinar el
comportamiento de ciertas funciones propias de estas ciencias (como la
oferta, demanda, costos, ingresos, etc.) cuando estas toman ciertos valores
peculiares. Para entender mejor esto consideremos el siguiente caso:
Ejemplo
Un productor de ropa deportiva determina que, dada la capacidad productiva
de su planta, podrá obtener mensualmente I ingresos (en miles de dólares) en
función de la cantidad de prendas producidas x (en cientos de unidades). Dicha
función está dada por: Ix=x2-x-6x-3
Determine los ingresos cuando la producción sea de 300 unidades (x=3).
A primera vista en este ejercicio pareciera sencillo determinar los ingresos que
el productor recibirá, únicamente sustituyendo x por 3; pero fijémonos lo que
pasa cuando hacemos eso:
I3=9-3-63-3=00 Indeterminación
Es aquí cuando entran en escena los límites; pues en base a lo obtenido
interpretamos que cuando la producción es de 300 unidades la capacidad
productiva de la planta habrá sido rebasada. Esto es lo que se debe hacer:

10. limx⟶3x2-x-6x-3=limx⟶3x-3(x+2) x-
3=limx⟶3x+2=limx⟶3x+limx⟶32=3+2=5
Entonces obtenemos la respuesta de que cuando la producción tiende a 300
unidades, el ingreso que percibirá el producto será de 5000 dólares.
Continuidad de una función
Intuitivamente decimos que una función es contínua cuando podemos
dibujarla con un sólo trazo del lápiz, es decir, sin levantar este del papel.

11. Discontinuidad
Las gráficas de la figura son discontinuas en el punto x=a, y lo son por
distintas razones. Las gráficas de 1 presentan asíntotas verticales (ramas
infinitas) en x=a. Las de 2 presentan un salto finito en x=a. Las gráficas de 3
no tienen definido f(a), o, teniéndolo definido (caso de la derecha), no
coincide con el valor en el entorno del mismo. En todos los casos resulta
imposible dibujar las gráficas con un sólo trazo del lápiz, con lo que no son
funciones continuas.
Aunque esta idea es una buena aproximación cuando estudiamos funciones a
partir de sus gráficas, no es suficientemente precisa. En este apartado vamos
a profundizar en el estudio de la continuidad de las funciones a través de los
siguientes puntos:
Continuidad en un punto
Si observas con detenimiento los distintos puntos de las gráficas anteriores
en los que las funciones sí son contínuas y los comparas con los puntos de
discontinuidad te percatarás de que:
Decimos que una función es continua en x=a cuando:
f(a)=limx→af(x)
Observa que la condición f(a)=limx→af(x), implica, en realidad, tres
condiciones:
1. La función está definida en x=a: ∃ f(a)
2. Existe el límite, y es finito: ∃limx→af(x)∈R. Esta condición implica que
los límites laterales coinciden: limx→a−f(x)=limx→a+f(x)
3. Finalmente, que los dos valores anteriores coinciden
Como ves, que una función sea continúa en un punto implica que la
función está definida en el punto y en un entorno del mismo. Aunque queda
fuera del alcance de este nivel, podemos dar una definición formal
basándonos en estas dos ideas:
Formalmente, decimos que una función f(x) es continua en a cuando, para
cualquier entorno de f(a) que fijemos, se puede encontrar un entorno

12. de a cuyas imágenes correspondientes estén contenidas en el entorno
de f(a). Esto implica:
1. ∃ f(a)2. ∀ε>0, ∃δ>0 | si |x−a|<δ⇒|f(x)−f(a)|<ε
Donde:
• ε: Es el valor que define el entorno de f(a) en el eje y
• δ: Es el valor que define el entorno de a en el eje x
Continuidad local
En 1, elementos de la definición formal de continuidad en un punto. Para
cualquier ε que escojas, radio del entorno de f(a) (zona de fondo azul), se
puede encontrar un entorno de a con radio δ (fondo verde), que tiene todas
sus imágenes en el interior del primer entorno. Esto no ocurre así si la
función no es continua. De manera que, en 2, a partir de un entorno
de f(a) (limitado de nuevo por f(a)+ε y f(a)+ε), podemos encontrar elementos
(x0) en el correspondiente entorno de a que no tienen sus imágenes en el
entorno señalado de f(a).
En realidad, la segunda condición se asemeja bastante a la propia definición
formal de límite en un punto.

13. Continuidad en un intervalo abierto
Decimos que una función es continua en un intervalo abierto (a,b) cuando es
continua en todos los puntos pertenecientes a dicho intervalo.
La definición anterior es aplicable a los intervalos infinitos. Así, las funciones
elementales que estudiamos normalmente, definidas por una sola expresión
analítica, como por ejemplo, f(x)=3x2
+3, f(x)=cos(x) ó f(x)=x−−√ son continuas
en todo su dominio.
Continuidad en intervalo abierto (a,b)
A la izquierda, en 1, la función es continua en todos los puntos del intervalo
abierto (a,b). Por ello decimos que es continua en el intervalo. A la derecha,
en 2, la función presenta un punto de discontinuidad en x=c, con lo que
decimos que la función no es continua en dicho intervalo. Por otro lado,
recuerda que para definir la continuidad en un punto es necesario que la
función esté definida en un entorno del propio intervalo. Observa, en 1, que
cualquier punto de los reales perteneciente a un intervalo abierto tiene un
entorno contenido en el propio intervalo, incluso los puntos próximos a los
extremos. Así, el punto a+0.01, muy próximo al extremo inferior a tiene un
entorno en el propio intervalo (a,b) que nos permite aplicar la definición de
continuidad. Si lo piensas, esto ocurre para cualquier valor concreto próximo
a los extremos del intervalo.

14. CONCEPTO DE DERIVADA
La derivada de una función matemática es la razón o velocidad de cambio de
una función en un determinado punto. Es decir, qué tan rápido se está
produciendo una variación.
Desde una perspectiva geométrica, la derivada de una función es la
pendiente de la recta tangente al punto donde se ubica x.
En términos matemáticos, la derivada de una función puede expresarse de la
siguiente forma:
En la fórmula, x es el punto en el que la variable toma el valor de x.
Asimismo, h es cualquier número. Este luego se igualará a cero pues, como
vemos en la imagen superior, debemos calcular el límite de la función cuando
h se acerca a cero.
Cabe recordar que, en general, la derivada es una función matemática que se
define como la tasa de cambio de una variable respecto a otra. Es decir, en
qué porcentaje aumenta o disminuye una variable cuando otra también se ha
incrementado o disminuido.
Debemos precisar que el límite de una función se define como la tendencia
de esta (a qué valor se aproxima) cuando uno de sus parámetros (en este
caso h) se acerca a un valor determinado.

15. En este caso, no ha sido necesario hallar el límite cuando h se acerca a cero,
pues el resultado de dividir f(x+h)-f(x) entre h da como resultado a
un número natural, y no a una expresión algebraica donde podamos
encontrar a h, como es el siguiente caso:

16. Veamos ahora otro ejemplo:
Luego, dividimos entre h:

17. Finalmente, encuentro el límite cuando h se acerca a 0:
REGLAS DE DERIVACION
En cálculo (rama de las matemáticas), la derivada representa cómo una
función cambia a medida que su entrada cambia.En términos poco rigurosos,
una derivada puede ser vista como cuánto está cambiando el valor de una
cantidad en un punto dado.
La derivada de una función en un valor de entrada dado describe la mejor
aproximación lineal de una función cerca del valor de entrada. Para funciones
de valores reales de una sola variable, la derivada en un punto representa el
valor de la pendiente de la recta tangente en la gráfica de la función en dicho
punto. En dimensiones más elevadas, la derivada de una función en un punto
es la transformación lineal que más se aproxima a la función en valores
cercanos de ese punto. Algo estrechamente relacionado es el diferencial de
una función.

18. 1.Para una constante ''a'':
·Si f(x)=a, su derivada es f '(x)=0
Ejemplo:
→ Si f(x)=16, su derivada es f '(x)=0
2. Para la función identidad f(x)= x.
·Si f(x)= x, su derivada es f '(x)= 1.
Ejemplo:
→Si f(x)= x,su derivada es f '(x) =1
3.Para una constante ''a'' por una variable ''x'':
·Si f(x)=ax, su derivada es f '(x)=a
Ejemplo:
→Si f(x)= 7x, su derivada es f '(x)= 7
4.Para una varibale ''x'' elevada a una potencia ''n'':
·Si f(x)=xⁿ, su derivada es f '(x)= nxⁿˉ¹
Ejemplo:
→Si f(x)= x², su derivada es f '(x)= 2x
5.Para una constante ''a'' por una varibale ''x' elevada a una potencia ''n''
·Si f(x)= axⁿ su derivada es f '(x)= anxⁿ̄ˉ¹
Ejemplo:
→Si f(x) = 4x², su derivada es f '(x)= 8x
6. Para una suma de funciones:
·Si f(x) = u(x) +v(x), su derivada es f '(x) = u'(x) + v'(x)
Ejemplo:
→Si f(x)= 3x²+4x, su derivada es f '(x) = 6x+4
7.La regla de producto.

19. ·Esta regla es útil cuando se tiene una funcion formada de la multiplicación
de polinomios, como por ejemplo: f(x)=(2x³+3)(3x³-5); la regla de producto es
:
Si ''u'' y ''v'' son los polinomios:
La función:f(x) = uv
Su derivada: f '(x) = u'v +uv'
Veamos un ejemplo:
¿Cuál es la derivada de f(x)= (2x³+3)(3x³-5)?
→Solución:
f(x)= (2x³+3)(3x³-5)
f(x)= (6x²)(3x³-5) + (2x³+3)(12x³)
Si es fácil simplificar la expresión,entonces debe simplificarse.
8. La regla de cociente.
·Esta regla es útil cuando se tiene una funcion formada de la división de
polinomios, como por ejemplo: f (x)= 2x³+3/3x²-5; la regla de cociente es:
Si ''u'' y ''v'' son los polinomios:
La función: f(x)= u/v
Su derivada: f '(x)= u'v- uv'/v²
Veamos un ejemplo:
¿Cuál es la derivada de f(x) = 2x³+3/3x²-5?
→Solución:
f(x) = 2x³+3/3x²-5
f '(x)= (6x²)(3x²-5)-(2x³+3)(12x³)/(3x²-5)²
Si es fácil simplificar la expresión,entonces debe simplificarse.
9.Regla de cadena.
·Esta regla es útil cuando se tiene una función formada por un polinomio
elevado a una potencia como por ejemplo: f(x) = (2x³+3)³; la regla de cadena
es:

20. Si ''u'' es el polinomio:
La funcíón: f(x)= uⁿ̄
Su derivada:f '(x) = n(u)ⁿˉ¹(u')̄
Veamos un ejemplo:¿Cuál es la derivada de f(x) = (2x³+3)³?
→Solución:
f(x)=(2x³+3)³
f '(x)=3(2x³+3)²(6x²)
f '(x)=18x²(2x³+3)²
MAXIMOS Y MINIMOS
Los máximos y mínimos de una función son los valores más grandes o
pequeños de ésta, ya sea en una región o en todo el dominio.
Los máximos y mínimos en una función f son los valores más grandes
(máximos) o más pequeños (mínimos) que toma la función, ya sea en una
región (extremos relativos) o en todo su dominio (extremos absolutos).
Los máximos y mínimos también se llaman extremos de la función.
Los extremos absolutos son los valores de una función f más grandes
(máximos) o más pequeños (mínimos) de todo el dominio.

21. ▪ El máximo absoluto de la función f es el valor más grande en todo
el dominio.
▪ El mínimo absoluto de la función f es el valor más pequeño en
todo el dominio.
Los extremos absolutos también reciben el nombre de extremos
globales.

22. Los extremos relativos de una función f son los valores más grandes
(máximos) o más pequeños (mínimos) de una región del dominio.
Los extremos relativos también son conocidos como extremos locales.
▪ La función f tiene en M un máximo relativo si f(M) es mayor que
sus valores próximos a izquierda y derecha.
En términos de sus derivadas, sean f y f ’ derivables en M.
Entonces M es máximo relativo de f si:
También se puede decir que M es un máximo relativo en su
entorno si a la izquierda la función es creciente y a la
derecha decreciente.
▪ La función f tiene en m un mínimo relativo si f(m) es menor que sus
valores próximos a izquierda y derecha.

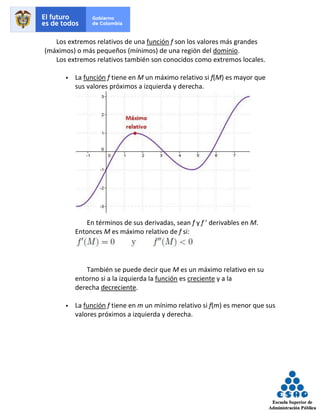
23. En términos de sus derivadas, sean f y f ’ derivables en m.
Entonces m es mínimo relativo de f si:
También se puede decir que m es un mínimo relativo en su
entorno si a la izquierda la función es decreciente y a la derecha
creciente.
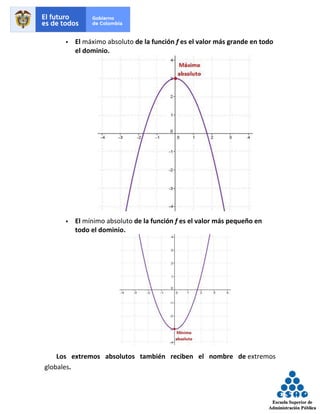
Este teorema confirma la existencia de un máximo absoluto y un mínimo
absoluto en una función continua definida en un intervalo cerrado [a,b], pero
no define como se calcula. Para calcularlos el procedimiento es el siguiente:
1. Derivar la función, obteniendo f ’(x).
2. Hallar las raíces de la derivada, es decir, los valores de x tales que
la derivada sea 0.
Supongamos que las raíces de f ’ son {r1, r2,…,rn}.
3. Se calcula la imagen de los extremos del intervalo (f(a) y f(b)).
También se calcula la imagen de las raíces ( f(r1) , f(r2) ,…, f(rn) ).
4. El máximo y mínimo absolutos de f serán:

24. Ejemplo
Encontrar el máximo absoluto y mínimo absoluto de la función f(x) en el
intervalo [-1,5], tal que:
Aplicaremos el procedimiento del teorema de los extremos.
1. Derivamos la función, obteniendo:
2. Hallamos las raíces de la derivada:
3. Las imágenes de los extremos del intervalo y de las dos raíces son:

25. 4. Por lo tanto, el máximo y mínimo absolutos de f serán:
Se han comparado cuatro imágenes de la función en cuatro
puntos, los dos en los que el valor de la derivada es nulo (0, 1) y
(3, -12,5) con los correspondientes a los extremos del intervalo (-
1, -4,5) y (5, 13,5). Resultado: máximo absoluto en el punto
(5, 13,5) y mínimo absoluto en el punto (3, -12,5).

26. APLICACIÓN DE LA DERIVADA
Las derivadas tienen muchas aplicaciones en el análisis de funciones.
En primer lugar, ofrece la pendiente de la recta tangente a la gráfica de
una función en un punto.
Pero tienen muchas más utilidades.
Esta lista, siguiendo el enlace, nos lleva a las más importantes aplicaciones
de las derivadas:
Estudiar la monotonía, es decir el crecimiento o el decrecimiento de
una función en un intervalo.

27. Para hallar los intervalos de monotonía de una función se realizará el
siguiente procedimiento:
1. Derivar la función, obteniendo f’(x).
2. Hallar las raíces de la derivada, es decir, los valores de x tales que en
ellos la derivada sea f’(x) = 0.
3. Crear intervalos abiertos con extremos las raíces halladas de f’(x).
4. Estudiar el signo que toma la derivada en un valor interior de cada
intervalo.

28. La derivada permite estudiar la concavidad o convexidad. La primera
derivada nos permite estudiar la curvatura (concavidad o convexidad) de
una función. La segunda derivada determina la curvatura.
En términos visuales, una función cóncava se asemeja a una montaña,
mientras que una función convexa a un valle.
(Hay autores que adoptan el criterio contrario, llamando cóncava a la
forma de valle y convexa a la forma de montaña).
Puntosdeinflexión
La derivada permite estudiar existencia de los puntos de inflexión.

29. Un punto de inflexión de una función es el lugar de su dominio en donde
cambia de curvatura, donde cambia de concavo a convexo o viceversa.
En un punto de inflexión, la tangente atraviesa la gráfica de la función. Si
además la primera derivada es nula, f’(a) = 0, es un punto de inflexión de
tangente horizontal.
Para que una función f(x) tenga un punto de inflexión en el punto (a, f(a))
es condición necesaria que la segunda derivada, si esta existe, sea nula en
dicho punto (f’’(a) = 0).
Esta condición es necesaria, pero no suficiente. Puede que sea f’’(a) = 0 y
no haber punto de inflexión en a. Pero, por el contrario, si fuese f’’(a) ≠ 0,
podemos afirmar que no hay un punto de inflexión en f(a).
Este sería el caso de la función f(x) = 2x4
. En ella, la segunda
derivada f’’(x) = 24x2
. Para x = 0, f’’(0) = 0 y, sin embargo, el punto (0, f(0)), es
decir, el punto (0, 0) no es un punto de inflexión, tal y como se ve en esta
imagen y se desarrollará en el ejercicio 2:

30. Tenemos dos criterios para averiguar si un punto x = a de una función, en
donde se verifique que f’’(a) = 0, se trata de un punto de inflexión:
5. Criterio de la segunda derivada
6. Criterio de la tercera derivada (o sucesivas)