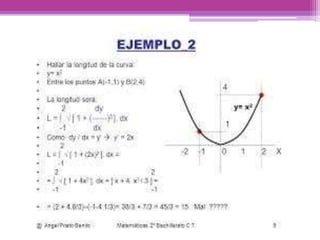
Este documento describe cómo calcular la longitud de una curva. Explica que la rectificación de una curva es la medida de la distancia recorrida a lo largo de ella y que cuando la curva es suave, la longitud de cada pequeño segmento se puede calcular usando el teorema de Pitágoras. También presenta la fórmula general para calcular la longitud total de una curva suave entre dos puntos.

2. Longitud de una curva
• Rectificación de una curva, es la medida
de la distancia o camino recorrido a lo
largo de una curva o dimensión lineal.
▫ Formula General

3. Si la primera derivada de una función
es continua en [a,b] se dice que es
suave y su gráfica es una curva suave.

4. • Cuando la curva es suave, la longitud de cada
pequeño segmentos de recta se puede
calcular mediante el teorema de Pitágoras
(dL)2=(dx)2+(dy)2.
• Si f es suave en [a,b], la longitud de la curva de
f(x) desde a hasta b es:

5. Ejemplo
• http://www.youtube.com/watch?v=QLFhBPOtF
4s
• Video Explicando ejercicio de longitud del arco
de una curva.