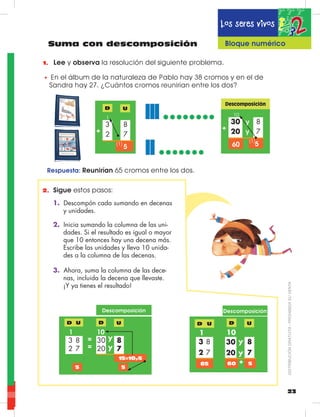
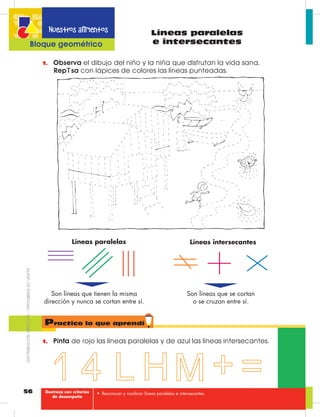
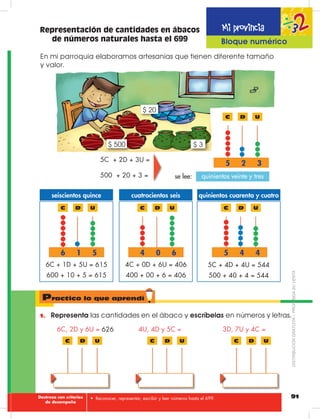
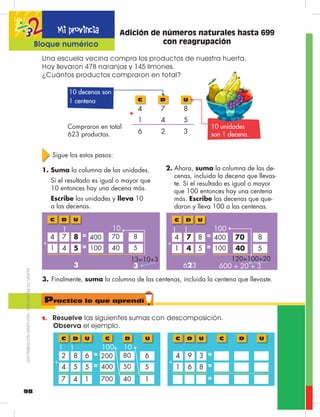
Este documento presenta información sobre la edición de libros de texto para la educación básica en Ecuador. Incluye los nombres de los editores y diseñadores del proyecto, así como información sobre el Ministerio de Educación de Ecuador y las autoridades gubernamentales involucradas en la edición de los libros.