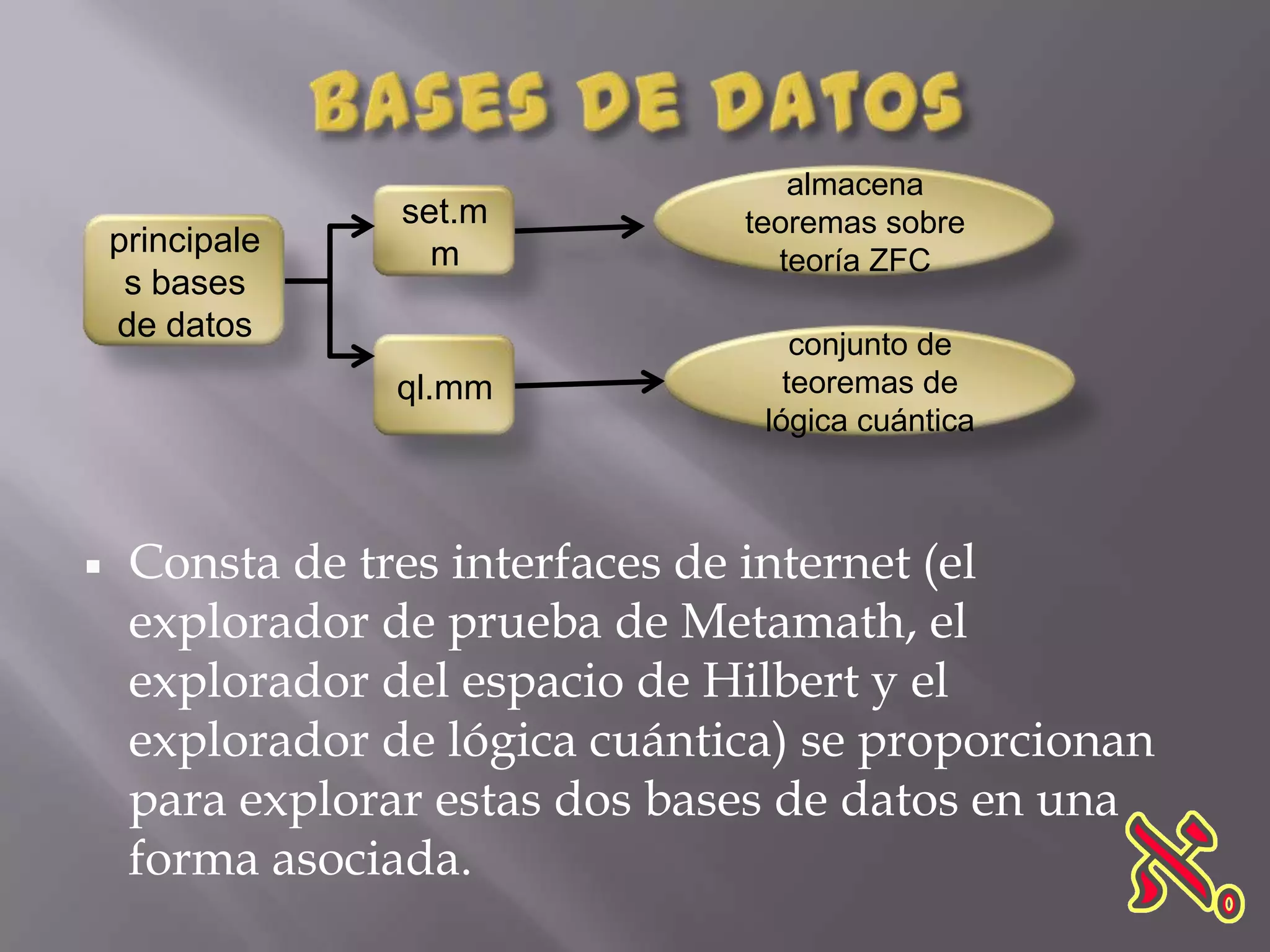
Metamath es un lenguaje diseñado para crear definiciones matemáticas formales y pruebas, acompañado de un comprobador y una base de datos de teoremas en diversas áreas de la matemática. Ofrece tres interfaces para explorar resultados como lógica y álgebra, pero su complejidad y detalle pueden hacer que su uso en educación sea poco recomendado. Aunque puede ser útil para el desarrollo personal de los estudiantes, no facilita la internalización efectiva de conocimientos teóricos.

1. Software libre
Luis Castillo Sepúlveda
Herna Solís Levicoi
Pedagogía en Matemática
y Computación

2.  Metamath es un lenguaje
para el desarrollo de las
definiciones matemáticas
estrictamente formales y
pruebas, acompañado de un
Comprobador de prueba para
este lenguaje y una creciente
base de datos de miles de
teoremas probados,
cubriendo resultados
convencionales en:  lógica.
 teoría de conjuntos.
 Teoría de números.
 Teoría de grupos.
 Álgebra.
 Análisis.
 Topología
 así como temas de
espacios de Hilbert y
lógica cuántica.

3. almacena
set.m teoremas sobre
principale m teoría ZFC
s bases
de datos
conjunto de
ql.mm teoremas de
lógica cuántica
 Consta de tres interfaces de internet (el
explorador de prueba de Metamath, el
explorador del espacio de Hilbert y el
explorador de lógica cuántica) se proporcionan
para explorar estas dos bases de datos en una
forma asociada.

4.  Normalmente los textos omiten muchos detalles a la hora
de explicar un teorema, implícitamente suponiendo que el
lector tenga un conocimiento profundo del material previo, el
cual Metamath no le proporcionará. Pero si sólo quieres la
capacidad de convencerte a ti mismo que una cadena de
símbolos matemáticos, que los matemáticos llaman
"teorema" es una consecuencia mecánica de los axiomas,
el método de prueba de Metamath, le permite lograrlo.

6. •La Simplicidad conceptual
de Metamath, ya que a •Metamath a
•Sólo se menudo se necesita un gran veces duda
pueden número de pasos para entre varias
ingresar los demostrar un teorema, y ver fórmulas para
nombres de todo el camino de vuelta explicar un
los teoremas hacia los axiomas podría Teorema, ya
a la consola. ser muy engorroso . Pero que analiza (la
No puede las pruebas han sido mayoría de
introducir verificadas por el equipo, y ellos sin
directamente el usuario puede elegir sentido) y pide
las fórmulas estudiar sólo los pasos que al usuario que
le interesen y tener plena elija.
confianza que el resto son
correctos.

7. Si bien los software pueden representar una importante
herramienta pedagógica, éstos software en particular no son
recomendables bajo nuestro punto de vista, porque aunque sean
muy útiles para el desarrollo personal del estudiantes, no tienen
mayores herramientas para que los conocimientos planteados de
forma teórica puedan ser internalizados de mejor forma mediante
su utilización.
•las pruebas en Metamath
son demasiado detallada
para ser utilizado con
facilidad en la escuela,
además consta de
comandos específicos.