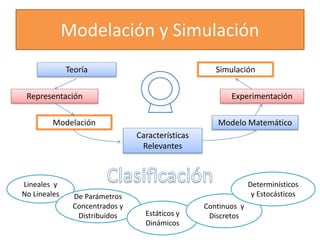
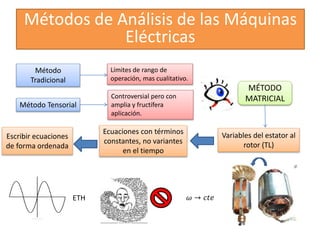
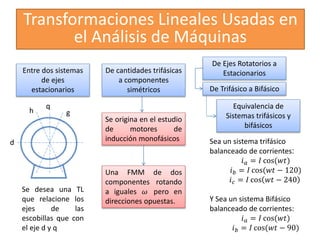
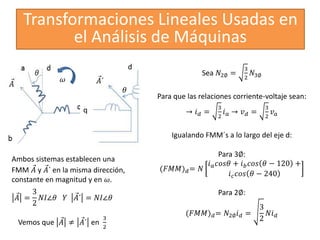
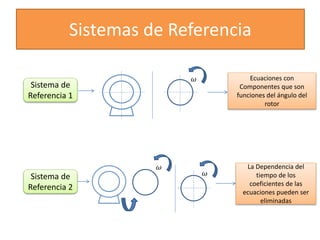
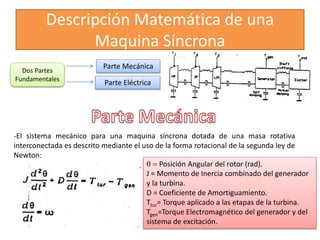
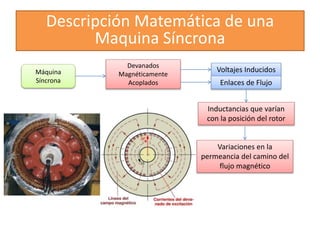
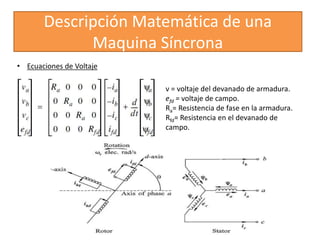
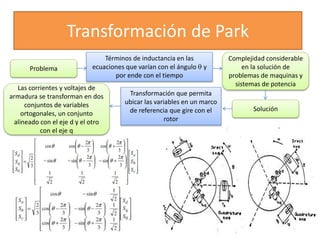
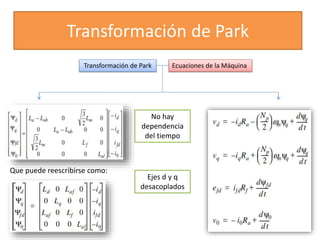
Este documento describe diferentes modelos matemáticos y transformaciones lineales utilizadas para el análisis de máquinas eléctricas. Explica la transformación de Park, la cual permite reescribir las ecuaciones de una máquina síncrona sin dependencia del tiempo al transformar las variables de corriente y voltaje del estator a un marco de referencia giratorio. También cubre otros modelos como el de dominio de fases y el de reactancia de voltaje de retorno.

1. Elaborado por
Anderson Calderón

2. Modelación y Simulación
Modelación
Representación
Características
Relevantes
Teoría
Modelo Matemático
Experimentación
Simulación
Lineales y
No Lineales De Parámetros
Concentrados y
Distribuidos Estáticos y
Dinámicos
Continuos y
Discretos
Determinísticos
y Estocásticos

3. Métodos de Análisis de las Máquinas
Eléctricas
MÉTODO
MATRICIAL
Método
Tradicional
Método Tensorial
Límites de rango de
operación, mas cualitativo.
Controversial pero con
amplia y fructífera
aplicación.
Variables del estator al
rotor (TL)
Ecuaciones con términos
constantes, no variantes
en el tiempo
Escribir ecuaciones
de forma ordenada
ETH 𝜔 → 𝑐𝑡𝑒

4. Transformaciones Lineales Usadas en
el Análisis de Máquinas
Entre dos sistemas
de ejes
estacionarios
g
q
h
d
Se desea una TL
que relacione los
ejes de las
escobillas que con
el eje d y q
De cantidades trifásicas
a componentes
simétricos
Se origina en el estudio
de motores de
inducción monofásicos
Una FMM de dos
componentes rotando
a iguales 𝜔 pero en
direcciones opuestas.
De Trifásico a Bifásico
Equivalencia de
Sistemas trifásicos y
bifásicos
Sea un sistema trifásico
balanceado de corrientes:
𝑖𝑎 = 𝐼 cos(𝑤𝑡)
𝑖𝑏 = 𝐼 cos(𝑤𝑡 − 120)
𝑖𝑐 = 𝐼 cos 𝑤𝑡 − 240
Y Sea un sistema Bifásico
balanceado de corrientes:
𝑖𝑎 = 𝐼 cos(𝑤𝑡)
𝑖𝑏 = 𝐼 cos(𝑤𝑡 − 90)
De Ejes Rotatorios a
Estacionarios

5. Transformaciones Lineales Usadas en
el Análisis de Máquinas
𝐴´
𝜃
Ambos sistemas establecen una
FMM 𝐴 y 𝐴´ en la misma dirección,
constante en magnitud y en 𝜔.
q
d
𝐴 =
3
2
𝑁𝐼∠𝜃 𝑌 𝐴´ = 𝑁𝐼∠𝜃
Vemos que 𝐴 ≠ 𝐴´ en
3
2
Sea 𝑁2∅ =
3
2
𝑁3∅
Para que las relaciones corriente-voltaje sean:
→ 𝑖𝑑 =
3
2
𝑖𝑎 → 𝑣𝑑 =
3
2
𝑣𝑎
Igualando FMM´s a lo largo del eje d:
Para 3∅:
(𝐹𝑀𝑀)𝑑= 𝑁
𝑖𝑎𝑐𝑜𝑠𝜃 + 𝑖𝑏𝑐𝑜𝑠 𝜃 − 120 +
𝑖𝑐𝑐𝑜𝑠 𝜃 − 240
Para 2∅:
(𝐹𝑀𝑀)𝑑= 𝑁2∅𝑖𝑑 =
3
2
𝑁𝑖𝑑
𝜔

6. Transformaciones Lineales Usadas en
el Análisis de Máquinas
Igualamos para obtener la equivalencia:
3
2
𝑁𝑖𝑑= 𝑁
𝑖𝑎𝑐𝑜𝑠𝜃 + 𝑖𝑏𝑐𝑜𝑠 𝜃 − 120 +
𝑖𝑐𝑐𝑜𝑠 𝜃 − 240
𝑖𝑑=
2
3
𝑖𝑎𝑐𝑜𝑠𝜃 + 𝑖𝑏𝑐𝑜𝑠 𝜃 − 120 +
𝑖𝑐𝑐𝑜𝑠 𝜃 − 240
Del mismo modo para 𝑖𝑞 tenemos:
𝑖𝑞=
2
3
𝑖𝑎𝑠𝑒𝑛𝜃 + 𝑖𝑏𝑠𝑒𝑛 𝜃 − 120 +
𝑖𝑐𝑠𝑒𝑛 𝜃 − 240
Debido a que 2 variables no pueden en
general, reemplazar a 3, debe existir una
ecuación de limitación que ligue a 𝑖𝑎 , 𝑖𝑏 e
𝑖𝑐.
En la mayoría de los casos de máquinas existe
la ecuación:
𝑖𝑎 + 𝑖𝑏 + 𝑖𝑐=0
Para Máquinas conectadas en Y.
Si la ecuación de limitación no existe el
sistema trifásico debe ser reemplazado por
otro sistema trifásico, para ello podemos
hacer el uso de la llamada corriente de
secuencia cero:
𝑖𝑜 =
1
3
(𝑖𝑎 + 𝑖𝑏 + 𝑖𝑐)
Luego, la transformación de trifásico a
bifásico es:

7. Transformaciones Lineales Usadas en
el Análisis de Máquinas
𝑖𝑑=
2
3
𝑖𝑎𝑐𝑜𝑠𝜃 + 𝑖𝑏𝑐𝑜𝑠 𝜃 − 120 +
𝑖𝑐𝑐𝑜𝑠 𝜃 − 240
𝑖𝑞=
2
3
𝑖𝑎𝑠𝑒𝑛𝜃 + 𝑖𝑏𝑠𝑒𝑛 𝜃 − 120 +
𝑖𝑐𝑠𝑒𝑛 𝜃 − 240
𝑖𝑜 =
1
3
(𝑖𝑎 + 𝑖𝑏 + 𝑖𝑐)
La Matriz Transformación es:
C=
2
3
𝑐𝑜𝑠𝜃 𝑐𝑜𝑠 𝜃 − 120 𝑐𝑜𝑠 𝜃 − 240
𝑠𝑒𝑛𝜃 𝑠𝑒𝑛 𝜃 − 120 𝑠𝑒𝑛 𝜃 − 240
1
2
1
2
1
2
La Matriz Inversa es:
𝐶−1
=
2
3
𝑐𝑜𝑠𝜃 𝑐𝑜𝑠 𝜃 − 120 𝑐𝑜𝑠 𝜃 − 240
𝑠𝑒𝑛𝜃 𝑠𝑒𝑛 𝜃 − 120 𝑠𝑒𝑛 𝜃 − 240
1
2
1
2
1
2
Al momento del análisis de una MS se usan distintos
sistemas de ejes de referencia para obtener sistemas
de ecuaciones sencillos para cada problema
particular.

8. Sistemas de Referencia
Sistema de
Referencia 1
𝜔 Ecuaciones con
Componentes que son
funciones del ángulo del
rotor
Sistema de
Referencia 2
𝜔
𝜔
La Dependencia del
tiempo de los
coeficientes de las
ecuaciones pueden ser
eliminadas

9. Descripción Matemática de una
Maquina Síncrona
Dos Partes
Fundamentales
Parte Mecánica
Parte Eléctrica
-El sistema mecánico para una maquina síncrona dotada de una masa rotativa
interconectada es descrito mediante el uso de la forma rotacional de la segunda ley de
Newton:
q = Posición Angular del rotor (rad).
J = Momento de Inercia combinado del generador
y la turbina.
D = Coeficiente de Amortiguamiento.
Ttur= Torque aplicado a las etapas de la turbina.
Tgen=Torque Electromagnético del generador y del
sistema de excitación.

10. Descripción Matemática de una
Maquina Síncrona
Máquina
Síncrona
Devanados
Magnéticamente
Acoplados
Voltajes Inducidos
Enlaces de Flujo
Inductancias que varían
con la posición del rotor
Variaciones en la
permeancia del camino del
flujo magnético

11. Derivación de Expresiones
Matemáticas
El enlace de flujos en la
fase a es:
La Componente de la FMM
de la fase a, 𝐹𝑎 , esta
conformada por 2
componentes, una del eje d
y otra del eje q:
Lo anterior puede ser
expresado como:
La auto-inductancia en la
fase a viene dada por:
De Igual manera se
determinan las fases b y c,
pero cambiando los
ángulos:

12. Descripción Matemática de una
Maquina Síncrona
Considerando una MS:
-Devanado de armadura de 3 fases.
-Devanado de campo.
-Rotor Cilíndrico
Es descrita mediante:
Dos Sistemas de
ecuaciones
• Relaciones Flujo-Corriente
Ψ =Enlace de flujo del devanado.
i = Corriente de Devanado.
La= auto-inductancia de una fase en la armadura.
Lab = Inductancia Mutua fase a fase en la armadura.
Lm=Inductancia Mutua entre el devanado de campo y la
fase pico en la armadura.
Lf = Auto-inductancia del devanado de campo.
q= Ángulo eléctrico entre el eje magnetico de la fase a
y el eje magnético del devandado de campo.
wm= Velocidad angular mecánica.
w = Velocidad Angular Eléctrica.
Np=Numero de polos magnéticos.
Esta matriz de inductancia es dependiente del tiempo

13. Descripción Matemática de una
Maquina Síncrona
• Ecuaciones de Voltaje
ν = voltaje del devanado de armadura.
efd = voltaje de campo.
Ra= Resistencia de fase en la armadura.
Rfd= Resistencia en el devanado de
campo.

14. Transformación de Park
Problema
Términos de inductancia en las
ecuaciones que varían con el ángulo q y
por ende con el tiempo
Complejidad considerable
en la solución de
problemas de maquinas y
sistemas de potencia
Solución
Transformación que permita
ubicar las variables en un marco
de referencia que gire con el
rotor
Las corrientes y voltajes de
armadura se transforman en dos
conjuntos de variables
ortogonales, un conjunto
alineado con el eje d y el otro
con el eje q

15. Transformación de Park
Transformación de Park Ecuaciones de la Máquina
Que puede reescribirse como:
No hay
dependencia
del tiempo
Ejes d y q
desacoplados

16. Otros Modelos
• Modelo de dominio de fases • Modelo de reactancia de voltaje de retorno
-Puede ser directamente incorporado a la red
(Ninguna transformación es requerida).
-Genera mas precisión (menos inestabilidad
numérica).
-Proporciona mas información (las soluciones en
simulaciones están mas relacionadas a las
cantidades físicas reales).
-Posee ventajas a la hora de simular sistemas de
potencia multi-maquina (no son necesarios
múltiples marcos de referencia).
-Ventajas en el modelado de la saturación
magnética.
-Requiere datos de inductancia propia y mutua de
varios devanados de la máquina (estos datos
generalmente no están disponibles).
-Carencia de verificaciones rigurosas en el desempeño.
-La existencia de términos variantes en el tiempo
aumenta la carga computacional.
-El circuito del estator es expresado en coordenadas
de fase y es directamente conectado a la red
externa.
-Las ecuaciones del rotor son expresadas en un
marco de referencia del rotor qd que
significativamente reduce la carga computacional.
-La formulación del modelo es muy flexible.
-Partición de las ecuaciones del rotor y el estator
provee un desacoplamiento natural de las escalas
de tiempo.
-Aumento del tiempo de ejecución computacional
debido a los elementos variantes en el tiempo.
-Carencia de verificaciones rigurosas en el desempeño
inter-máquina.