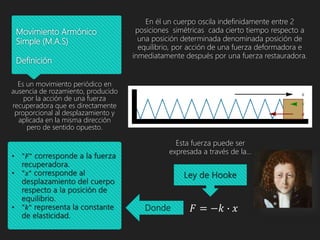
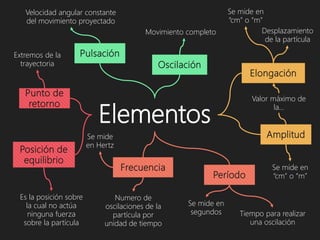
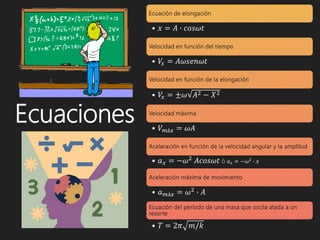
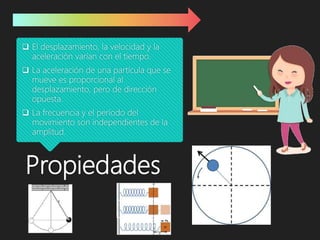
El movimiento armónico simple (m.a.s) es un tipo de movimiento periódico donde un cuerpo oscila entre dos posiciones simétricas alrededor de una posición de equilibrio debido a fuerzas en acción. Se caracteriza por su indefinición en duración, variable desplazamiento, y se describe mediante la ley de Hooke, que relaciona la fuerza restauradora con el desplazamiento. Las propiedades incluyen variaciones en desplazamiento, velocidad y aceleración, además de que la frecuencia y el período son independientes de la amplitud.

1. Movimiento Armónico Simple

2. Esquema
1. Definición
2. Características
3. Elementos
4. Ecuaciones
5. Propiedades
6. Relación con la vida diaria y el proyecto

3. Movimiento Armónico
Simple (M.A.S)
Definición
En él un cuerpo oscila indefinidamente entre 2
posiciones simétricas cada cierto tiempo respecto a
una posición determinada denominada posición de
equilibrio, por acción de una fuerza deformadora e
inmediatamente después por una fuerza restauradora.
Es un movimiento periódico en
ausencia de rozamiento, producido
por la acción de una fuerza
recuperadora que es directamente
proporcional al desplazamiento y
aplicada en la misma dirección
pero de sentido opuesto.
𝐹 = −𝑘 ∙ 𝑥
Ley de Hooke
Esta fuerza puede ser
expresada a través de la…
Donde
• "𝐹“ corresponde a la fuerza
recuperadora.
• "𝑥“ corresponde al
desplazamiento del cuerpo
respecto a la posición de
equilibrio.
• "𝑘“ representa la constante
de elasticidad.

4. Características
Es un movimiento periódico, es decir, se repite con
similares en intervalos de tiempo iguales.
Su duración es indefinida mientras no sufra algún
rozamiento que varíe las fuerzas actuando sobre el
Sin la acción de ninguna fuerza el cuerpo se mantiene en
posición de equilibrio
Es la proyección de la trayectoria de un movimiento circular
uniforme.

5. Elementos
Oscilación
Elongación
Amplitud
Período
Frecuencia
Posición de
equilibrio
Punto de
retorno
Pulsación
Movimiento completo Desplazamiento
de la partícula
Valor máximo de
la…
Tiempo para realizar
una oscilación
Se mide en
“cm” o “m”
Se mide en
segundos
Se mide en
“cm” o “m”
Numero de
oscilaciones de la
partícula por
unidad de tiempo
Es la posición sobre
la cual no actúa
ninguna fuerza
sobre la partícula
Se mide
en Hertz
Extremos de la
trayectoria
Velocidad angular constante
del movimiento proyectado

6. Ecuaciones
Ecuación de elongación
• 𝑥 = 𝐴 ∙ 𝑐𝑜𝑠𝜔𝑡
Velocidad en función del tiempo
• 𝑉𝑥 = 𝐴𝜔𝑠𝑒𝑛𝜔𝑡
Velocidad en función de la elongación
• 𝑉𝑥 = ±𝜔 𝐴2 − 𝑋2
Velocidad máxima
• 𝑉 𝑚á𝑥 = 𝜔𝐴
Aceleración en función de la velocidad angular y la amplitud
• 𝑎 𝑥 = −𝜔2
𝐴𝑐𝑜𝑠𝜔𝑡 ó 𝑎 𝑥 = −𝜔2
∙ 𝑥
Aceleración máxima de movimiento
• 𝑎 𝑚á𝑥 = 𝜔2
∙ 𝐴
Ecuación del período de una masa que oscila atada a un
resorte
• 𝑇 = 2𝜋 𝑚/𝑘

7. Propiedades
 El desplazamiento, la velocidad y la
aceleración varían con el tiempo.
 La aceleración de una partícula que se
mueve es proporcional al
desplazamiento, pero de dirección
opuesta.
 La frecuencia y el período del
movimiento son independientes de la
amplitud.