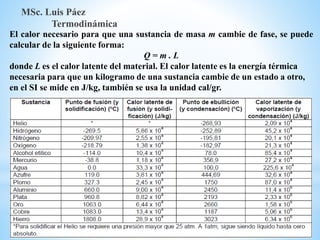
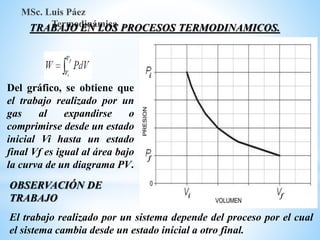
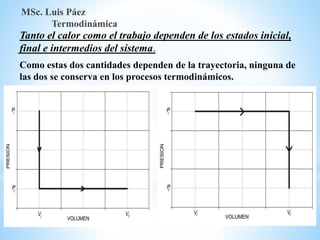
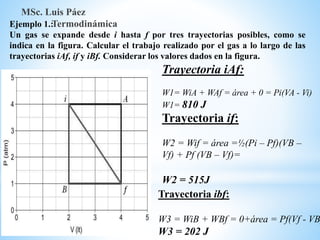
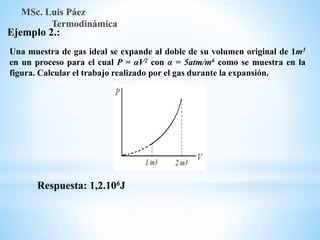
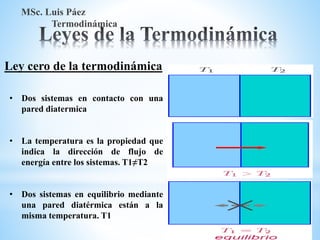
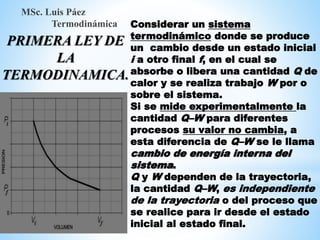
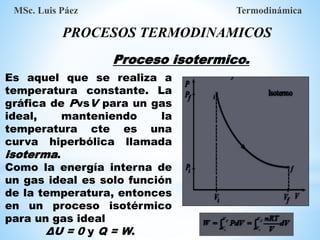
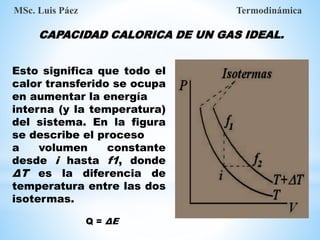
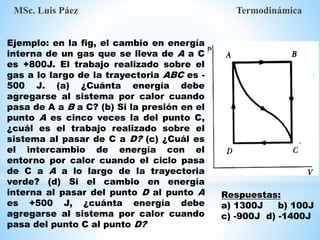
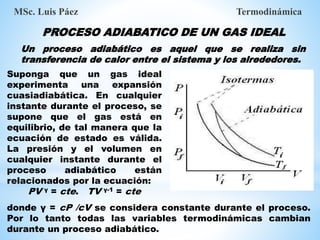
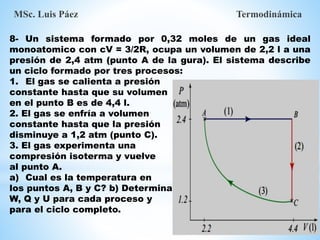
1. El documento describe los requisitos de asistencia, exámenes y evaluación para la clase de Termodinámica. Los estudiantes deben asistir a al menos el 70% de las clases teóricas y el 100% de las clases prácticas.
2. Habrá dos exámenes parciales que representarán el 35% de la calificación final, así como trabajos de laboratorio que representarán el 5%.
3. El examen final representará el 60% de la calificación final.