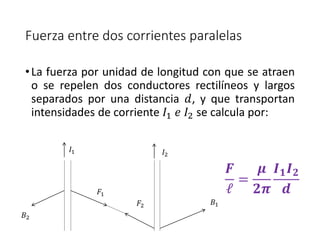
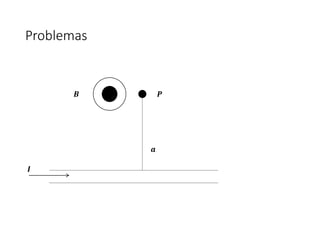
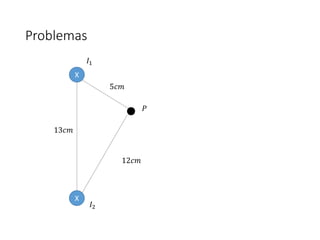
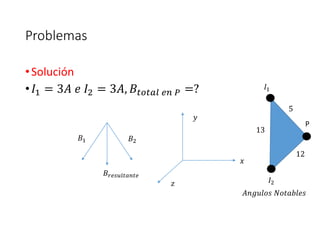
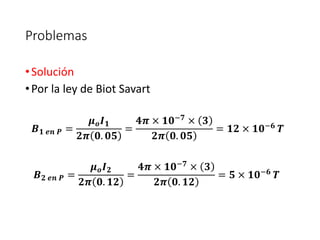
Este documento trata sobre las fuentes de campos magnéticos. Explica la ley de Biot-Savart para calcular el campo magnético producido por corrientes eléctricas. También cubre el campo magnético creado por cargas en movimiento, alambres rectos, espiras circulares y solenoides. Finalmente, presenta algunos problemas de aplicación de estas leyes.

1. Fuentes de Campos
Magnéticos
Clase 10
07-Noviembre-2014

2. Fuentes de Campos Magnéticos
• En el tema anterior se verificaba de un campo magnético por la
fuerza que se ejercía sobre una carga eléctrica en movimiento. En
este tema se resolverán problemas sobre la producción de campos
magnéticos.

3. Ley de Biot-Savart
• Después de muchas experiencias, se llego a al
conclusión de que los campos magnéticos son
producidos por cargas en movimiento, esto es, por
corrientes eléctricas. Los físicos Biot y Savart
dedujeron una relación matemática que permite
conocer el campo magnético 푑퐵 en un punto 푃
debido a un elemento de corriente 푑푆 que conduce
una intensidad de corriente 퐼 es:
풅푩 =
흁
ퟒ흅
푰풅풔 × 풓
풓ퟐ

4. Ley de Biot-Savart
•Donde:
• 휇 es la permeabilidad magnética del medio, en el
S.I. para el vacío:
흁 = ퟒ흅 × ퟏퟎ−ퟕ 푾풃
푨 ∙ 풎
• 푟 es la distancia del punto al elemento de corriente.

5. Ley de Biot-Savart
• Para calcular el campo magnético que produce un
conductor que lleva una corriente, se debe integrar
el vector 풅푩 en toda longitud del conductor.

6. Campo magnético creado por una carga
eléctrica en movimiento
• Se define el campo magnético creado por una carga
푞 que se mueve con una velocidad 푣 en un punto
situado a una distancia 푟 de ella, mediante la
expresión
푩 =
흁
ퟒ흅
풒
풗 × 풓
풓ퟑ

7. Campo magnético de un alambre recto y
largo
• El campo magnético creado por una corriente
rectilínea indefinida a una distancia 푎 se obtiene
mediante
푩 =
흁푰
ퟐ흅풂

8. Campo magnético creado por una espira
circular conductora en su centro
푩 =
흁푰
ퟐ풓
• Donde 푟es el radio de la espira e 퐼 es la intensidad
de corriente eléctrica que circula por la espira.

9. Campo magnético en el interior de un
solenoide
푩 = 흁
푵
푳
푰 = 흁풏푰
• Donde 푁 es el número de espiras, 퐿 es la longitud
del solenoide, 퐼 la intensidad de corriente que
circula por él y 푛 es el número de espiras por
unidad de longitud.

10. Fuerza entre dos corrientes paralelas
• La fuerza por unidad de longitud con que se atraen
o se repelen dos conductores rectilíneos y largos
separados por una distancia 푑, y que transportan
intensidades de corriente 퐼1 푒 퐼2 se calcula por:
푭
ℓ
=
흁
ퟐ흅
푰ퟏ푰ퟐ
풅
퐼1 퐼2
퐹1
퐹2 퐵1
퐵2

11. Fuerza entre dos corrientes paralelas
• Cuando las intensidades de corriente son del mismo
sentido existen entre ellas fuerzas atractivas;
cuando las intensidades de corriente son de sentido
contrario, las fuerzas son repulsivas.

12. Definición del ampere
• Se define el ampere como la intensidad de una
corriente que, circulando en el mismo sentido por
dos conductores rectilíneos y paralelos separados
por el vacío por la distancia de un metro, origina en
cada uno de ellos una fuerza atractiva de 2 ×
10−7 푁 por metro de longitud.

13. Ley de Ampere (no generalizada)
• Establece que la integral de línea de 퐵 ∙ 푑푠 a lo largo
de cualquier trayectoria cerrada es igual a 휇퐼 donde
퐼 es una intensidad de corriente constante que pasa
a través de cualquier superficie delimitada por la
trayectoria cerrada. Matemáticamente se expresa
por:
푩 ∙ 풅풔 = 흁푰

14. Problemas
• Problema 1
• Un alambre de cobre desnudo del #10 puede conducir una
intensidad de corriente de 50 A sin sobrecalentarse. Si se hace
circular una intensidad de corriente de esta magnitud por una
sección larga y recta de alambre del #10. ¿A que distancia del eje del
alambre la magnitud del campo magnético resultante es igual a
10−3푇?

15. Problemas
푰
푩 푷
풂

16. Problemas
• Solución
• Datos 퐼 = 50 퐴, 퐵 = 10−3푇
• La magnitud del campo magnético debido a un alambre infinito a una
distancia 푎, está dado por:
푩 =
흁풐푰
ퟐ흅풂

17. Problemas
• Despejando 푎 y sustituyendo valores, se tiene
푎 =
휇표퐼
2휋퐵
=
4휋 × 10−7 50
2휋 10−3
푎 = 0.01 푚 ó 3.18 × 10−3푚

18. Problemas
• Problema 2
• Dos largos conductores paralelos conducen las
corrientes 퐼1 = 3퐴 푒 퐼2 = 3퐴. Ambas dirigidas hacia
adentro de la figura. Determine la magnitud y
dirección del campo magnético resultante en P.

19. Problemas
X
X
5푐푚
12푐푚
13푐푚
퐼1
퐼2
푃

20. Problemas
• Solución
• 퐼1 = 3퐴 푒 퐼2 = 3퐴, 퐵푡표푡푎푙 푒푛 푃 =?
퐵1 퐵2
퐵푟푒푠푢푙푡푎푛푡푒
푥
푧
푦
퐼1
퐼2
5
13
12
P
퐴푛푔푢푙표푠 푁표푡푎푏푙푒푠

21. Problemas
• Solución
• Por la ley de Biot Savart
푩ퟏ 풆풏 푷 =
흁풐푰ퟏ
ퟐ흅 ퟎ. ퟎퟓ
=
ퟒ흅 × ퟏퟎ−ퟕ × ퟑ
ퟐ흅 ퟎ. ퟎퟓ
= ퟏퟐ × ퟏퟎ−ퟔ 푻
푩ퟐ 풆풏 푷 =
흁풐푰ퟐ
ퟐ흅 ퟎ. ퟏퟐ
=
ퟒ흅 × ퟏퟎ−ퟕ × ퟑ
ퟐ흅 ퟎ. ퟏퟐ
= ퟓ × ퟏퟎ−ퟔ 푻

22. Problemas
• Solución
• Luego:
• 퐵푟푒푠푢푙푡푎푛푡푒 푒푛 푃 = 퐵1
2 + 퐵2
2
• 퐵푟푒푠푢푙푡푎푛푡푒 푒푛 푃 = 12 × 10−6 2 + 5 × 10−6 2
• 퐵푟푒푠푢푙푡푎푛푡푒 푒푛 푃 = 13 × 10−6푇 (hacia abajo)

23. Problemas
• Problema 3
• En la teoría de Bohr del átomo de hidrogeno puede
pensarse que el electrón se mueve en una orbita
circular de radio 5.3 × 10−11푚 con una velocidad
tangencial de 2.2 × 106푚/푠. Calcule la magnitud
del campo magnético producido por el movimiento
del electrón en la posición del protón.

24. Problemas
• Problema 3
푃
푅
푒

25. Problemas
• Solución
• Datos
• 푞 = 1.6 × 10−19퐶, 푅 = 5.3 × 10−11푚, 푣 = 2.2 × 106 푚/푠
• La magnitud del campo magnético en el centro de una espira circular
que lleva una corriente, esta dado por
퐵 =
휇표 퐼
2푅
• Por otro lado, al corriente se define como la cantidad de carga que pasa
por una cierta región del espacio entre el intervalo de tiempo que tarda
en pasar la cantidad de carga. Y como 푓 es el numero de veces que el
electrón pasa por un punto dado por unidad de tiempo, la carga total
que pasa por cierta región por unidad de tiempo esta dada por (que es la
intensidad de corriente).
퐼 =
푛ú푚푒푟표 푑푒 푣푒푐푒푠 푞푢푒 푝푎푠푎 푝표푟 푒푙 푒푙푒푐푡푟ó푛
푢푛푖푑푎푑 푑푒 푡푖푒푚푝표
푞 = 푓푞

26. Problemas
• Solución
• Pero 푓 es el inverso del periodo, 푇 y por la definición del periodo, se
tiene
푓 =
1
푇
=
1
2휋푅
푣
=
푣
2휋푅
• Sustituyendo la frecuencia en la expresión de la intensidad de corriente,
se tiene
퐼 =
푣푞
2휋푅

27. Problemas
• Solución
• sustituyendo la intensidad de corriente en al expresión del campo
magnético y sustituyendo valores, se tiene
퐵 =
휇표푣푞
4휋푅2 =
4휋 × 10−7 2.2 × 106 1.6 × 10−19
4휋 5.3 × 10−11 2 = 12.53 × 10−12 푇

28. Problemas
• Problema 4
• Un estudiante fabrica un electroimán con una bobina
delgada de largo 4.8cm por donde circula una intensidad de
corriente de 11.5 A. ¿Cuántas vueltas deberá tener la bobina
para producir un campo magnético 6.3 mT en el centro?
ℓ
퐼

29. Problemas
• Solución
• Datos ℓ = 4.8 × 10−2푚, I = 11.5 A, B = 6.3 × 10−3푇
• La magnitud del campo magnético en el interior de una bobina esta
dado por
푁 =
퐵ℓ
휇표퐼
=
6.3 × 10−3 4.8 × 10−2
4휋 × 10−7 11.5
= 21 푣푢푒푙푡푎푠

30. Problemas
• Problema 5
• A un alambre que conduce una corriente de 5A se le va a dar forma
de una espira circular de una vuelta. Si el valor requerido del campo
magnético en el centro de la espira es 10휇푇, ¿Cuál es el radio
requerido?

31. Problemas
• Solución
푑푠
퐼 푟
푂
푥
푧
푦
Datos
퐼 = 5퐴
퐵 푒푛 0 = 10휇푇
푅 =?

32. Problemas
• Solución
• Sabemos que:
• 푑퐵 푒푛 0 =
휇표∙퐼
4휋푅2 푑푠 × 푟 =
휇0∙퐼∙푑푠
4휋푅2
• ⟹ 퐵 푒푛 0 = 푑퐵 =
2휋
휇0∙퐼
4휋푅2 0
푅 ∙ 푑휃
• =
휇0퐼
4휋푅2 휃 0 2휋
• ∴ 푩풆풏 ퟎ =
흁ퟎ푰
ퟐ푹

33. Problemas
• Solución
• Luego, reemplazando tenemos
10−6 4휋×10−7× 5
• 10 × =
2푅
• ∴ 푅 = 0.314 푚