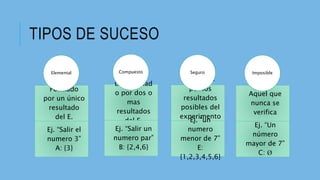
Este documento explica las diferencias entre combinaciones, permutaciones y probabilidad. Combinaciones y permutaciones se refieren a las diferentes formas en que se pueden agrupar elementos, dependiendo de si el orden es o no importante. La probabilidad se refiere a la posibilidad de que ocurra un suceso específico en un experimento aleatorio, expresada como la relación entre el número de resultados favorables y el total de resultados posibles.

1. COMBINACIONES,
PERMUTACIONES Y
PROBABILIDAD.

2. PERMUTACI
ONES Y
COMBINACIO
NES

3. ¿QUÉ DIFERENCIA HAY?
"Mi ensalada de frutas es una combinación de manzanas,
uvas y bananas":
"La combinación de la cerradura es 472":
Normalmente usamos la palabra "combinación"
descuidadamente, sin pensar en si el orden de las cosas es
importante. En otras palabras:
Así que en estadística usamos un lenguaje más preciso:
 Si el orden no importa, es una combinación.
 Si el orden sí importa es una permutación.

4. COMBINACIONES
Se llama combinaciones de
m elementos tomados de n
en n (m ≥ n) a todas las
agrupaciones posibles que
pueden hacerse con los m
elementos.

5. SIN REPETICIÓN.
No entran todos los
elementos.
No importa el orden.
No se repiten los elementos.
𝑪 𝒎
𝒏
=
𝒎!
𝒎 − 𝒏 ! 𝒏!
Ejemplo:
Se sortean 2 laptops iguales entre
10 personas. ¿De cuantas formas se
puede escoger a los ganadores?
CON REPETICIÓN.
No entran todos los elementos.
No importa el orden.
Sí se repiten los elementos.
𝑪𝑹 𝒎
𝒏
=
(𝒎+𝒏−𝟏)!
𝒎−𝟏 ! 𝒏!
Ejemplo:
En una bodega hay 5 diferentes
tipos de botellas. ¿De cuantas
formas se pueden elegir 4 botellas?

6. PERMUTACIONES
Se llama permutaciones de m
elementos (m = n) a las
diferentes agrupaciones de esos
m elementos
Permutaciones con
repetición de n elementos donde
el primer elemento se
repite a veces , el segundo
b veces , el tercero c veces, ...

7. SIN REPETICIÓN.
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.
𝑷 𝒏 = 𝒏!
Ejemplo:
En una carrera participan 4
caballos: A, B, C y D. ¿De cuantas
formas pueden terminar la carrera?
CON REPETICIÓN.
Sí entran todos los elementos.
Sí importa el orden.
Sí se repiten los elementos.
𝑷𝑹 𝒂𝒃𝒄
𝒏
=
𝒏!
𝒂!𝒃!𝒄!
Ejemplo:
En una urna hay 5 bolas del mismo
tamaño y peso. ¿De cuantas formas
se pueden extraer una a una las
pelotas teniendo en cuenta que hay
3 rojas y 2 azules?

8. ¿QUÉ ES LA PROBABILIDAD?
La probabilidad de un suceso
es un número, comprendido
entre 0 y 1, que indica las
posibilidades que tiene de
verificarse cuando se realiza
un experimento aleatorio.
Ésta establece una relación
entre el número de sucesos
favorables y el número total
de sucesos posibles.

9. POR EJEMPLO
Por ejemplo, lanzar un
dado, y que salga el
número uno (caso
favorable) está en
relación a seis casos
posibles (1, 2, 3, 4, 5 y
6); es decir, la
probabilidad es 1/6.

10. ¿QUÉ ES UN EXPERIMENTO
ALEATORIO?
Son aquellos en los que no
se puede predecir el
resultado, ya que éste
depende del azar.
Ejemplos:
 Si lanzamos una moneda
no sabemos de antemano
si saldrá cara o cruz.
Si lanzamos un dado
tampoco podemos
determinar el resultado
que vamos a obtener.

11. ¿QUÉ ES EL ESPACIO MUESTRAL?
Es el conjunto de todos los posibles resultados de
una experiencia aleatoria, lo representaremos por E.
Espacio muestral de una moneda:
E = {C, X}.
Espacio muestral de un dado:
E = {1, 2, 3, 4, 5, 6}.

12. ¿QUÉ ES UN SUCESO?
Se llama suceso a
cualquier
subconjunto del
espacio muestral.
Hay varios tipos de
sucesos, dentro de los
cuales podemos
mencionar:
 Suceso
elemental.
 Suceso
compuesto
 Suceso seguro
 Suceso
imposible.

13. TIPOS DE SUCESO
Formado
por un único
resultado
del E.
Ej. “Salir el
numero 3”
A: {3}
Elemental
Determinad
o por dos o
mas
resultados
del E.
Ej. “Salir un
numero par”
B: {2,4,6}
Compuesto
Formado
por los
resultados
posibles del
experimento
.
Ej. “un
numero
menor de 7”
E:
{1,2,3,4,5,6}
Seguro
Aquel que
nunca se
verifica
Ej. “Un
número
mayor de 7”
C: Ø
Imposible