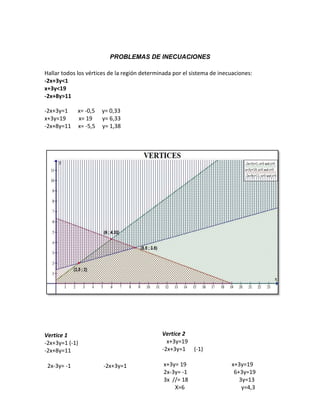
Este documento presenta cinco problemas de optimización que involucran inecuaciones y sistemas de inecuaciones. Cada problema describe una situación con recursos limitados y objetivos de maximización, y se resuelve determinando la combinación óptima de variables que maximice la función objetivo.

1. PROBLEMAS DE INECUACIONES
Hallar todos los vértices de la región determinada por el sistema de inecuaciones:
-2x+3y<1
x+3y<19
-2x+8y>11
-2x+3y=1 x= -0,5 y= 0,33
x+3y=19 x= 19 y= 6,33
-2x+8y=11 x= -5,5 y= 1,38
Vertice 1 Vertice 2
-2x+3y=1 (-1) x+3y=19
-2x+8y=11 -2x+3y=1 (-1)
2x-3y= -1 -2x+3y=1 x+3y= 19 x+3y=19
2x-3y= -1 6+3y=19
3x //= 18 3y=13
X=6 y=4,3

2. -2x+8y=11 -2x+3(2)=1
// 5y=10 x=2,5
y=2
Vertice 3 Solución:
x+3y=19 (2) x+ 3y =19 Vertice 1= (2,5 ; 2)
-2x+8y=11 x+3(3,5)=19 Vertice 2= (6 ; 4,33)
x =19-10.5
Vertice 3= (8,5 ; 3,5)
2x+6y= 38 x =8,5
-2x+8y=11
// 14y= 49
y=3,5
1. Un comerciante tiene dos tipos de café mezcla: tipo A con 10% de café torrado, tipo B
con 30% de café torrado. Se quiere una mezcla de 100 kg que tenga por lo menos 15%
de café torrado. El café tipo B cuesta $5 y el tipo A $4. ¿Cuál es la mezcla más
conveniente para que el costo sea mínimo?
4A+5B=Z
A+B<=100
0,10 A + 0,30 >=0,15(A+B) 0,10 A + 0,30 >=0,15(A+B)
0,10 A + 0,30 >=0,15A+0,15B
-0,05 A + 0,15 >=0 (1000)
-50 A+150B>=0
A+B<=100 A=100 B=100 A = 75
-50 A+150B>=0 A=75 B=25 (-50)(75)+150B = 0
150B= 3750
B=25

3. -50 A+150B=0
A+B=100 (50)
-50 A+150B=0 A+B=100
50A+ 50B=5000 A=100-25
// 200B=5000 A=75
B=25
SOLUCIÓN.-
2. Una empresa de muebles fabrica mesas y sillas de comedor. Cada silla necesita 2
metros de tabla y 4 horas de trabajo. Cada mesa 5 metros de madera y sólo 3 horas de
trabajo. El fabricante tiene 300 metros de madera disponibles y un equipo humano
capaz de proporcionar 380 horas de trabajo. Por último, el fabricante ha determinado
que hay una utilidad de $3 por cada silla vendida y $6 por cada mesa vendida.
¿Cuántas mesas y sillas se deben producir para maximizar las utilidades, suponiendo
que se vende todo objeto producido?
3A+ 6B=Z
2A+5B<=300 A=150 B=60
4A+3B<=380 A=95 B=126,67

4. 2A+5B=300 (-2)
4A+3B=380
-4A-10B= -600 2A+5B=300
4A+3B=380 2A =300-5(31,44)
// -7B = -220 A = 71,4
B= 31,44
3A+ 6B=Z
SOLUCIÓN. Se debe fabricar
3(71,4)+5(31,44)=Z
Sillas = 71
Z=371,4 Mesas = 31
3. Una hostería tiene un lago donde cría dos tipos de peces R y S. El peso promedio de
cada pez en 4Kg para R y 2Kg para S. Se dispone de dos tipos de alimento. A y B. Las
necesidades promedio de un pez de especie R son de 1 unidad de A y 3 unidades de B
diariamente. Las necesidades del pez S son 2 unidades de A y 1 unidad de B por día. Si
se cuenta con 500 unidades de A y 900 unidades de B, ¿cómo debe ser la cantidad de

5. peces de cada clase para maximizar el peso de peso de pescado que se pueda
producir?
4R + 2S = Z
R + 2S <= 500 A= 500 B= 250
3R+S<= 900 A=300 B=900
R + 2S = 500 (-3)
3R+S= 900
-3R – 6S = -1500 3R+S=900 4R + 2S=Z
3R + S = 900 3R = 900-120 4(260)+2(120)=Z
// -5S=-600 R = 260 1280=Z
S=120
SOLUCIÓN.-Se debe tener
Peces R = 260
Peces S = 120

6. 4. Una asociación recibió una donación de 100 bolígrafos y 150 lápices, y los va a vender
para recaudar fondos. Se decide armar paquetes de dos tipos. Los paquetes tipo A
tienen dos bolígrafos y dos lápices y se venden a $3. Los paquetes B tienen un
bolígrafo y dos lápices y se venden a $2. ¿Cuántos paquetes de cada tipo deben
vender para obtener la máxima ganancia
3A + 2B =Z
2A+B<=100 A=50 B=100
2A+2B<=150 A=75 B=75
2A+B=100 (-1)
2A+2B=150
-2A – B =-100 2A+2B = 150 3A + 2B =Z
2A+2B = 150 2A = 150-2(50) 3(25)+2(50)=Z
// B=50 A = 25 Z =175

7. SOLUCIÓN.- Se deben vender
Tipo A=25
Tipo B=50
5. Una empresa de viajes debe despachar por lo menos 750 cajas. Dispone de un camión
con capacidad para 100 cajas una camioneta con capacidad para 50 cajas. El camión
no puede hacer más viajes que la camioneta, y en total no pueden hacer más de 10
viajes. Si el costo de cada viaje es de $8 para el camión y de $6 para la camioneta,
¿Cuántos viajes deben hacer cada vehículo para que el costo de transporte sea
mínimo? ¿cuál es su costo?
8A + 6B = Z
100A + 50B<=750 A=7,5 B=15
A+B<=10 A= 10 B=10
A<=B
A=3
A-B=0
3-B=0
B=3

8. 100A + 50B=750
A + B =10 (-100)
100A + 50B=750 A + B=10
-100A-100B=-1000 A = 10-5
// -50 B = -250 A= 5
B =5
SOLUCION: los viajes que se deberan hacer son:
Camión = 5
Camioneta = 5