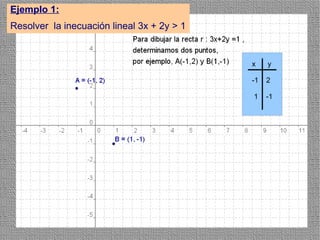
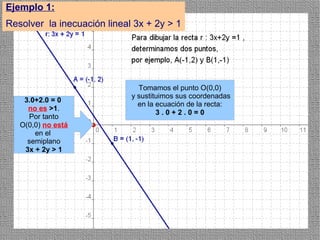
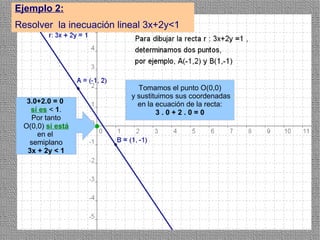
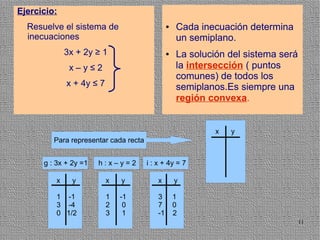
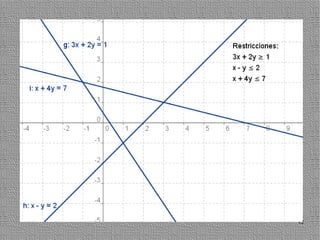
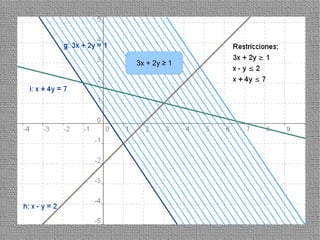
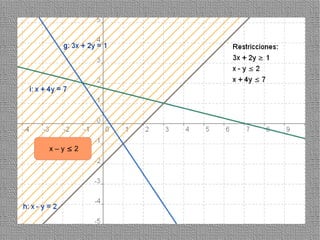
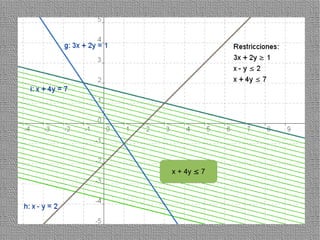
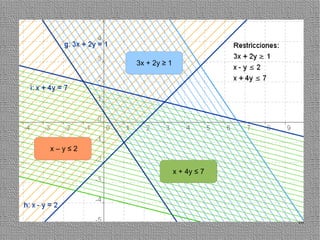
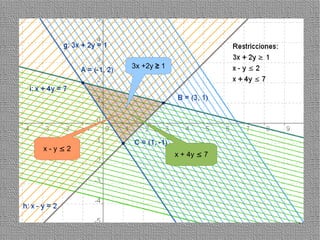
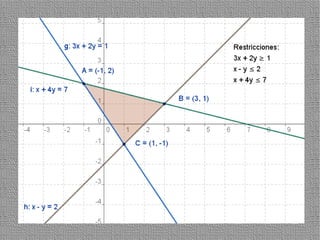
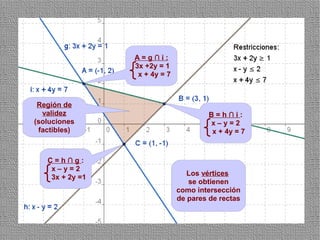
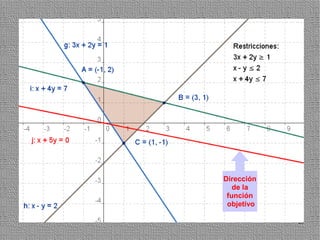
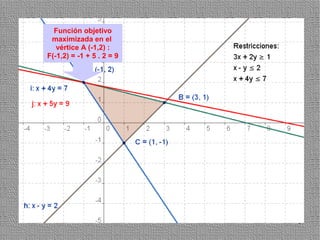
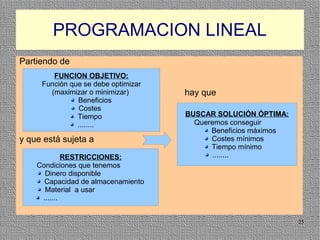
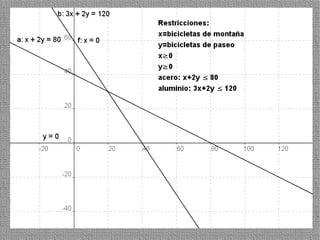
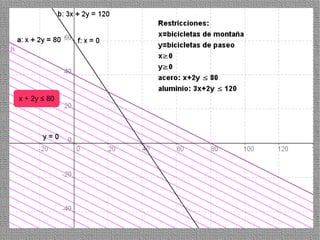
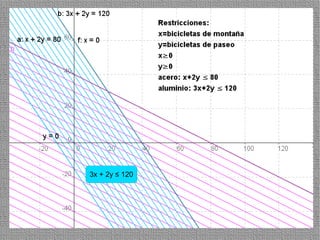
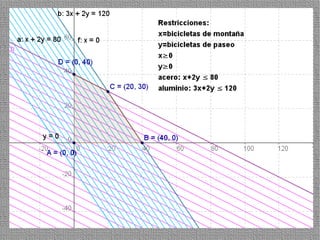
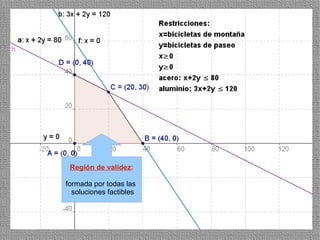
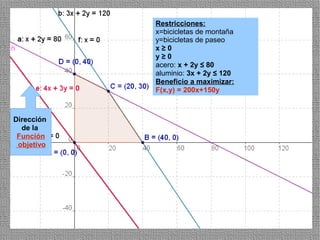
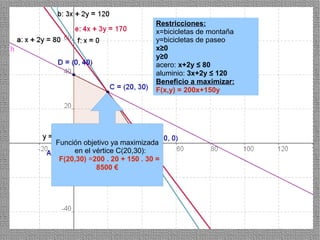
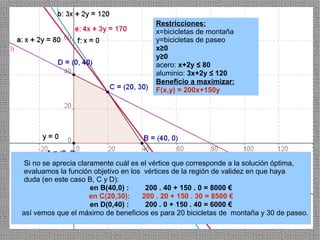
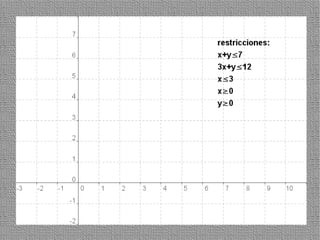
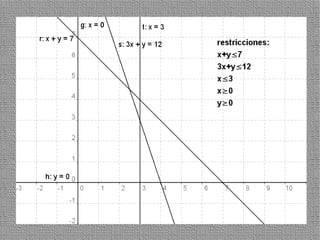
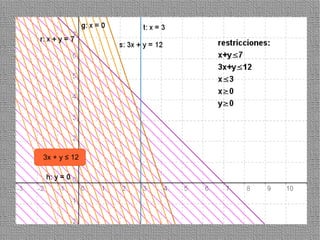
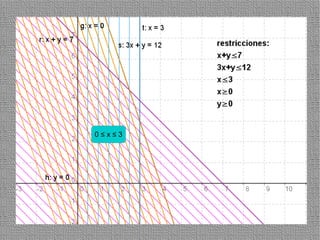
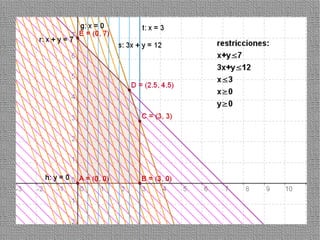
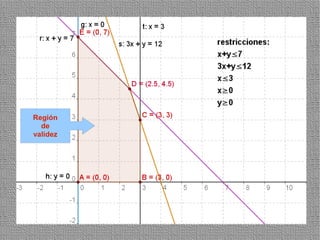
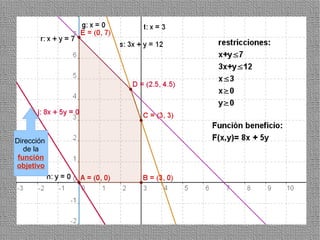
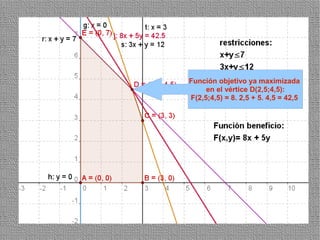
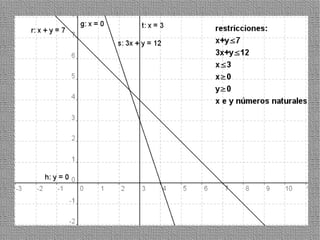
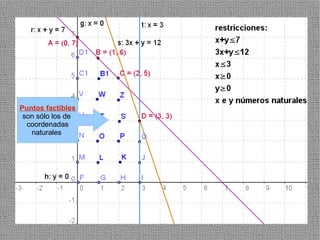
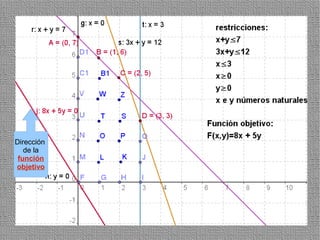
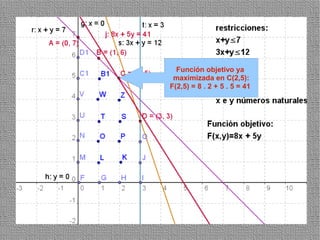
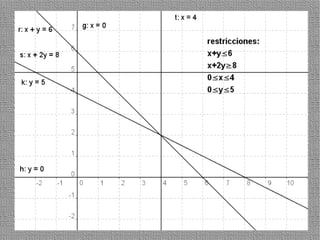
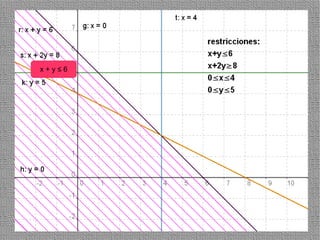
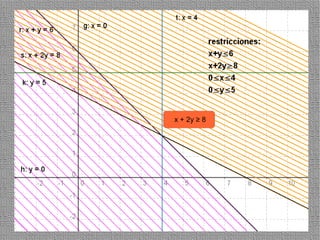
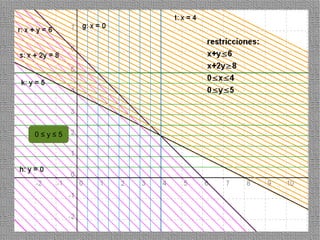
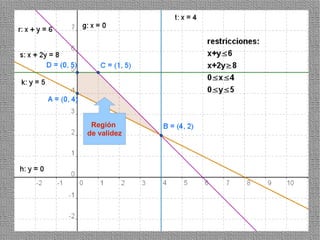
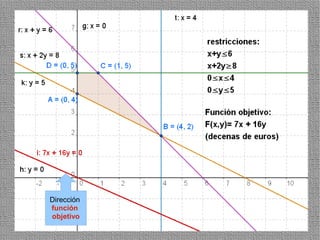
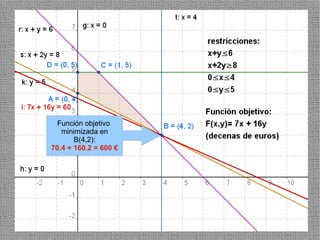
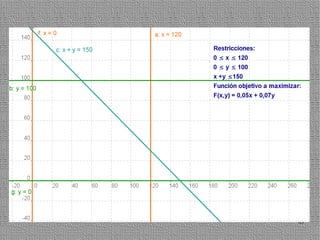
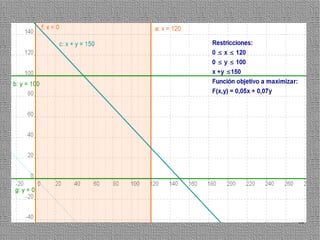
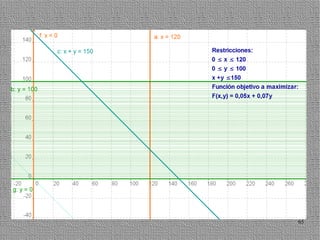
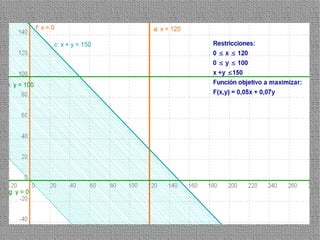
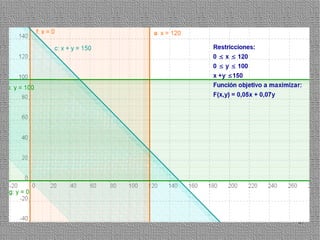
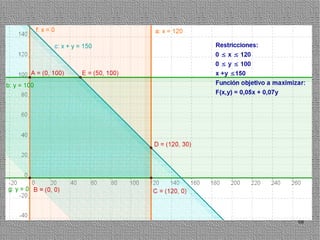
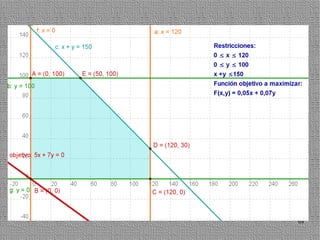
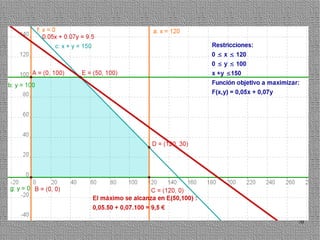
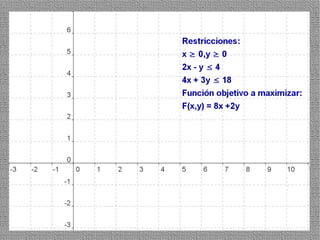
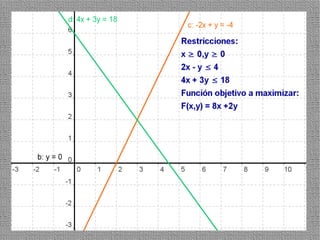
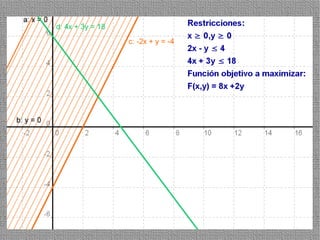
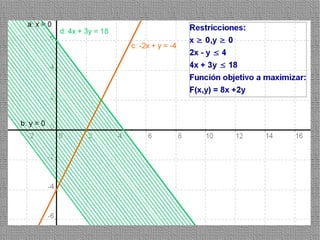
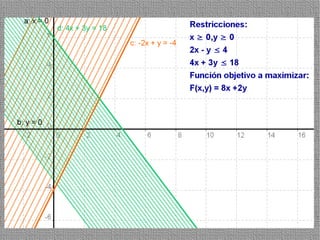
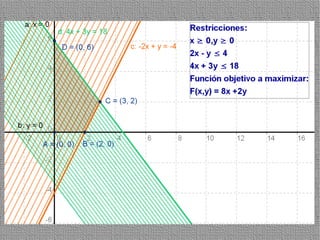
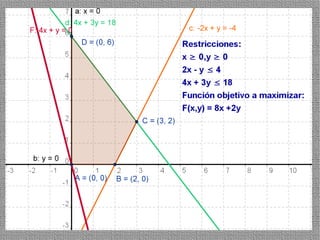
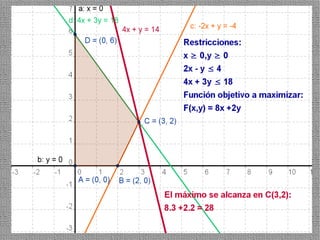
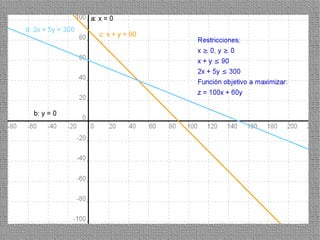
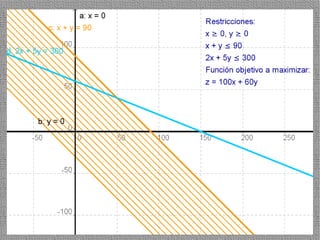
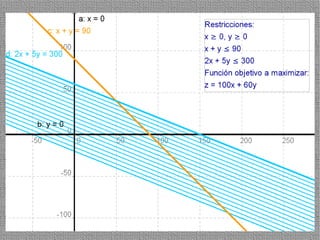
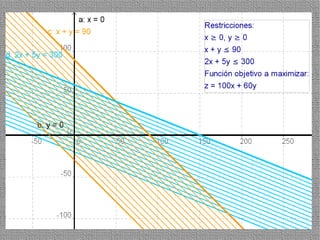
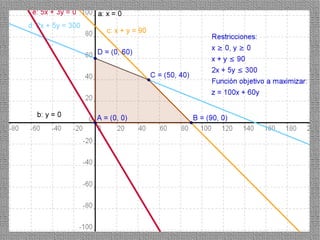
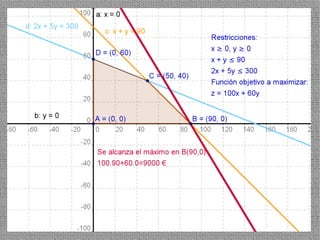
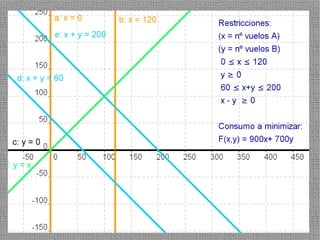
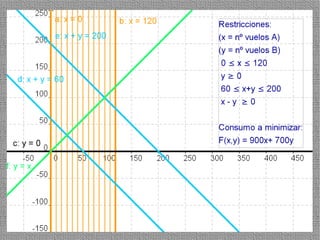
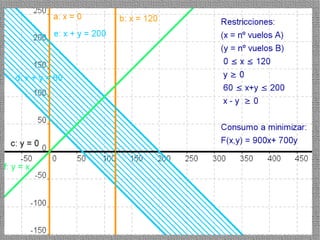
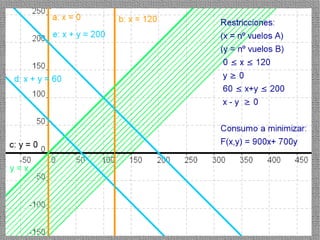
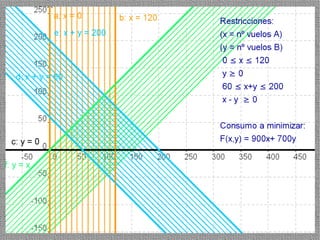
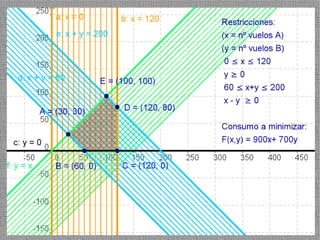
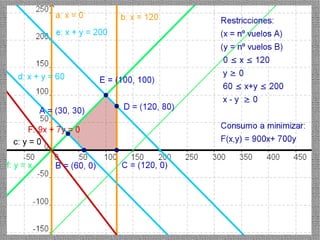
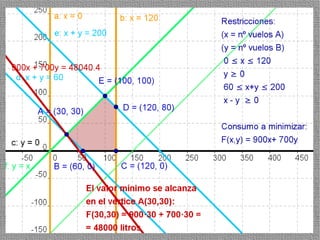
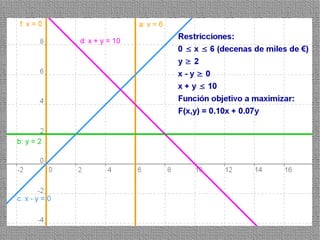
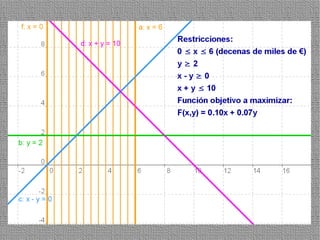
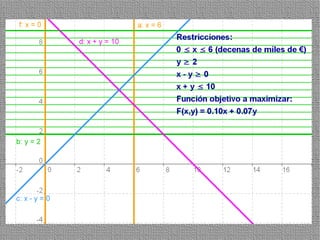
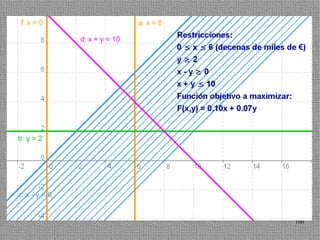
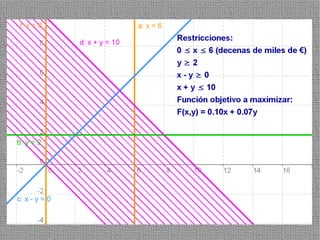
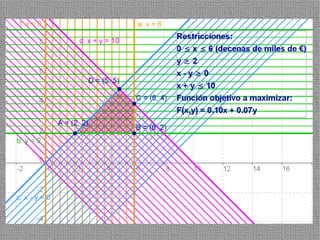
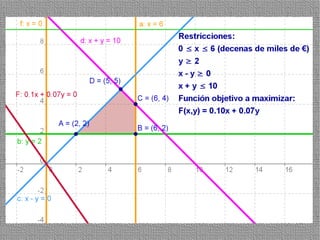
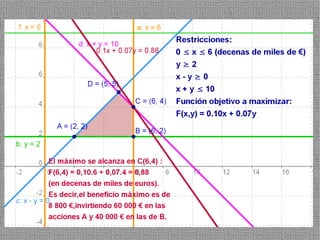
La programación lineal es un método para encontrar la solución óptima cuando se quiere optimizar una función objetivo lineal sujeta a restricciones lineales. Se representan las restricciones como semiplanos y la intersección de éstos da la región de validez. La solución óptima se encuentra en un vértice de dicha región.

1. PROGRAMACIÓN
LINEAL
Dantzig Koopmans
Kantorovich
© Inmaculada Leiva Tapia I.E.S.Alborán

2. 1.
INECUACIONES LINEALES
CON 2 INCÓGNITAS
2

3. Ejemplo 1:
Resolver la inecuación lineal 3x + 2y > 1
x y
-1 2
1 -1
3

4. Ejemplo 1:
Resolver la inecuación lineal 3x + 2y > 1
Tomamos el punto O(0,0)
y sustituimos sus coordenadas
3.0+2.0 = 0
en la ecuación de la recta:
no es >1.
3.0+2.0=0
Por tanto
O(0,0) no está
en el
semiplano
3x + 2y > 1
4

5. Ejemplo 1:
Resolver la inecuación lineal 3x + 2y > 1
O(0,0) es
exterior
al semiplano
3x + 2y > 1
3x + 2y > 1
5

6. Ejemplo 2:
Resolver la inecuación lineal 3x+2y<1
Tomamos el punto O(0,0)
y sustituimos sus coordenadas
3.0+2.0 = 0 en la ecuación de la recta:
sí es < 1. 3.0+2.0=0
Por tanto
O(0,0) sí está
en el
semiplano
3x + 2y < 1
6

7. Ejemplo 2:
Resolver la inecuación lineal 3x+2y<1
Tomamos el punto O(0,0)
y sustituimos sus coordenadas
en la ecuación de la recta:
O(0,0) es 3.0+2.0=0
interior
al semiplano
3x + 2y < 1
3x + 2y < 1
7

8. INECUACIONES LINEALES
CON 2 INCÓGNITAS
RESUMEN Resolver la inecuación:
3x+2y > 1
Sus soluciones forman un
semiplano.Para determinarlo:
Se representa la recta
3x+2y=1.
Se toma un punto que no
esté en la recta,por ej.,el
origen (0,0) y se sustituye en es2.0 < 1
(0,0) + exterior
3.0
la inecuación.
Si la cumple,se toma el
semiplano que contiene al
(0,0);y si no,el otro
semiplano. 8

9. 2.
SISTEMAS DE INECUACIONES
LINEALES CON 2 INCÓGNITAS
9

10. SISTEMAS DE INECUACIONES
LINEALES CON 2 INCÓGNITAS
Ejercicio:
● Cada inecuación determina Resuelve el sistema de
un semiplano. inecuaciones
● La solución del sistema será 3x + 2y ≥ 1
la intersección ( puntos x–y≤2
comunes) de todos los
x + 4y ≤ 7
semiplanos.Es siempre una
región convexa.
10

11. Ejercicio:
Resuelve el sistema de ● Cada inecuación determina
inecuaciones un semiplano.
3x + 2y ≥ 1 ● La solución del sistema será
x–y≤2 la intersección ( puntos
comunes) de todos los
x + 4y ≤ 7 semiplanos.Es siempre una
región convexa.
x y
Para representar cada recta
g : 3x + 2y =1 h:x–y=2 i : x + 4y = 7
x y x y x y
1 -1 1 -1 3 1
3 -4 2 0 7 0
0 1/2 3 1 -1 2
11

12. 12

13. 3x + 2y ≥ 1
13

14. x–y≤2
14

15. x + 4y ≤ 7
15

16. 3x + 2y ≥ 1
x–y≤2
x + 4y ≤ 7
16

17. 3x +2y ≥ 1
x-y≤2
x + 4y ≤ 7
17

18. 18

19. A=g∩i:
3x +2y = 1
x + 4y = 7
Región de
validez B=h∩i:
(soluciones x–y=2
factibles) x + 4y = 7
C=h∩g:
x–y=2
Los vértices
3x + 2y =1
se obtienen
como intersección
de pares de rectas
19

20. 3.
PROGRAMACIÓN LINEAL
20

21. PROGRAMACION LINEAL
Ejercicio:
La programación lineal es un
Resuelve el sistema de
método para obtener la opción inecuaciones
más conveniente, u opción 3x + 2y ≥ 1
óptima ,en situaciones en las x–y≤2
que la función que se quiere
x + 4y ≤ 7
optimizar( hacer máxima o
y maximiza con esas
mínima) depende de unas restricciones la función objetivo
variables sujetas a ciertas F(x,y) = x + 5y
restricciones.
21

22. Ejercicio:
Resuelve el sistema de
inecuaciones
3x + 2y ≥ 1
x–y≤2
Practica con Geogebra
x + 4y ≤ 7
y maximiza con esas
restricciones la función objetivo
F(x,y) = x + 5y
22

23. Dirección
de la
función
objetivo
23

24. Función objetivo
maximizada en el
vértice A (-1,2) :
F(-1,2) = -1 + 5 . 2 = 9
24

25. PROGRAMACION LINEAL
Partiendo de
FUNCION OBJETIVO:
Función que se debe optimizar
(maximizar o minimizar) hay que
Beneficios
Costes
Tiempo BUSCAR SOLUCIÓN ÓPTIMA:
........ Queremos conseguir
Beneficios máximos
y que está sujeta a Costes mínimos
Tiempo mínimo
RESTRICCIONES: ........
Condiciones que tenemos
Dinero disponible
Capacidad de almacenamiento
Material a usar
.......
25

26. En los problemas de programación lineal con dos variables
tenemos:
Una función objetivo F(x,y) lineal que hay que optimizar.
Puede representarse mediante una recta móvil.
Varias restricciones,dadas mediante inecuaciones lineales.
Cada una de ellas tiene como solución un semiplano.
Todas las restricciones juntas dan lugar a una región poligonal
convexa (región de validez) que puede ser finita o infinita.
Las soluciones factibles son los puntos de la región de validez,
y cumplen todas las restricciones a la vez.
26

27. En los problemas de programación lineal con dos variables
tenemos:
La solución óptima se encuentra siempre en la periferia de la región
de validez y puede ser: única ( vértice), infinitas ( lado ) o no existir.
Para determinar los vértices de la región de validez,se resuelven
los sistemas formados por los pares de rectas que determinan
los lados de dicha región.
Para optimizar la función objetivo,se mueve la recta que la representa,
paralelamente a sí misma,hasta encontrar el punto donde alcanza el
máximo o mínimo (solución óptima).
27

28. 4.
EJERCICIOS
28

29. Restricciones: EJERCICIO 1:
x = bicicletas de montaña Con 80 Kg de acero y 120 kg de
y = bicicletas de paseo aluminio,se quieren fabricar
x≥0 bicicletas de montaña y de paseo
y≥0 que se venderán a 200 y 150 €,
acero: x + 2y ≤ 80 respectivamente.
aluminio: 3x + 2y ≤ 120
Para la de montaña se necesitan
1 kg de acero y 3 kg de aluminio,
Beneficio a maximizar:
mientras que para la de paseo se
requieren 2 kg de cada metal.
F(x,y) = 200x+150y
¿Cuántas bicicletas de cada clase
se deben fabricar para obtener el
máximo beneficio?¿A cuánto
ascenderá este beneficio ?
Practica con Geogebra
29

30. 30

31. x + 2y ≤ 80
31

32. 3x + 2y ≤ 120
32

33. 33

34. Región de validez:
formada por todas las
soluciones factibles
34

35. Restricciones:
x=bicicletas de montaña
y=bicicletas de paseo
x≥0
y≥0
acero: x + 2y ≤ 80
aluminio: 3x + 2y ≤ 120
Beneficio a maximizar:
F(x,y) = 200x+150y
Dirección
de la
Función
objetivo
35

36. Restricciones:
x=bicicletas de montaña
y=bicicletas de paseo
x≥0
y≥0
acero: x+2y ≤ 80
aluminio: 3x+2y ≤ 120
Beneficio a maximizar:
F(x,y) = 200x+150y
Función objetivo ya maximizada
en el vértice C(20,30):
F(20,30) =200 . 20 + 150 . 30 =
8500 €
36

37. Restricciones:
x=bicicletas de montaña
y=bicicletas de paseo
x≥0
y≥0
acero: x+2y ≤ 80
aluminio: 3x+2y ≤ 120
Beneficio a maximizar:
F(x,y) = 200x+150y
Si no se aprecia claramente cuál es el vértice que corresponde a la solución óptima,
evaluamos la función objetivo en los vértices de la región de validez en que haya
duda (en este caso B, C y D):
en B(40,0) : 200 . 40 + 150 . 0 = 8000 €
en C(20,30): 200 . 20 + 150 . 30 = 8500 €
en D(0,40) : 200 . 0 + 150 . 40 = 6000 €
así vemos que el máximo de beneficios es para 20 bicicletas de montaña y 30 de paseo.
37

38. EJERCICIO 2:
Halla los valores de x e y que
hacen máxima la función
z = 8x + 5y
sujeta a las siguientes
restricciones:
x+y≤7
3x + y ≤ 12
x≤3
x≥0
y≥0
Practica con GeoGebra
38

39. 39

40. 40

41. x+y≤7
41

42. 3x + y ≤ 12
42

43. 0≤x≤3
43

44. 44

45. Región
de
validez
45

46. Dirección
de la
función
objetivo
46

47. Función objetivo ya maximizada
en el vértice D(2,5;4,5):
F(2,5;4,5) = 8. 2,5 + 5. 4,5 = 42,5
47

48. EJERCICIO 3:
Halla los valores de x e y que
hacen máxima la función
z = 8x + 5y
sujeta a las siguientes
restricciones:
x+y≤7
3x + y ≤ 12
x≤3
x≥0
y≥0
x , y deben ser números
naturales.
Practica con GeoGebra
48

49. 49

50. Puntos factibles
son sólo los de
coordenadas
naturales
50

51. Dirección
de la
función
objetivo
51

52. Función objetivo ya
maximizada en C(2,5):
F(2,5) = 8 . 2 + 5 . 5 = 41
52

53. Restricciones:
EJERCICIO 4:
x = nº microbuses
y = nº autobuses Un club de jubilados quiere
0≤x≤4 organizar un viaje para 200 socios.
0≤y≤5
x+y≤6 Contratan una agencia que
(25x + 50y ≥ 200) → x + 2y ≥ 8 dispone de 4 microbuses de 25
plazas y 5 autobuses de 50, pero
Coste a minimizar: solamente dispone de 6
conductores.
F(x,y) = 7x + 16y
(en decenas de euros) El alquiler de los autobuses
es de 160 € por día y el de los
microbuses de 70 € por día.
¿Cómo deben hacer para que el
coste del viaje sea el menor
posible?¿Cuál será dicho coste?
Practica con GeoGebra
53

54. 54

55. x+y≤6
55

56. x + 2y ≥ 8
56

57. 0≤x≤4
57

58. 0≤y≤5
58

59. Región
de validez
59

60. Dirección
función
objetivo
60

61. Función objetivo
minimizada en
B(4,2):
70.4 + 160.2 = 600 €
61

62. EJERCICIO 5:
Restricciones: Un estudiante reparte propaganda en su
tiempo libre.La empresa A le paga 0,05 €
(x = nº folletos de empresa A) por impreso repartido y la empresa B, con
(y = nº folletos de empresa B) folletos más grandes, le paga 0,07 € por
0 ≤ x ≤ 120 impreso.
0 ≤ y ≤ 100
x + y ≤ 150 El estudiante lleva dos bolsas: una para
los impresos de tipo A, en la que le caben
Beneficio a maximizar: 120, y otra para los de tipo B, en la que sólo
caben 100.
F(x,y) = 5x +7y
( en céntimos de € ) Ha calculado que cada día puede repartir
150 impresos como máximo.
¿Cuántos impresos habrá de repartir de
cada clase para que su beneficio diario sea
Practica con GeoGebra máximo?
62

63. 63

64. 64

65. 65

66. 66

67. 67

68. 68

69. 69

70. 70

71. EJERCICIO 6:
Restricciones:
Una industria vinícola produce vino y
x = nº unidades de vino vinagre.
y = nº unidades de vinagre
x ≥ 0,y ≥ 0 El doble de la producción de vino es
2x - y ≤ 4 siempre menor o igual que la de vinagre
4x + 3y ≤ 18 más cuatro unidades.
Beneficio a maximizar: Además,el triple de la producción de
vinagre más cuatro veces la producción
F(x,y) = 8x +2y de vino es siempre menor o igual que 18
unidades.
Halla el número de unidades de cada
producto que se deben producir para
alcanzar un beneficio máximo,sabiendo
Practica con GeoGebra que cada unidad de vino deja beneficio
de 8 €,y cada unidad de vinagre 2 €.
71

72. 72

73. 73

74. 74

75. 75

76. 76

77. 77

78. 78

79. 79

80. Restricciones: EJERCICIO 7:
x = nº plazas de fumadores Un autobús Madrid-París ofrece plazas
y = nº plazas de no fumadores para fumadores al precio de 100 €, y para
x ≥ 0, y ≥ 0 no fumadores al precio de 60 €.
x + y ≤ 90
2x + 5y ≤ 300 Al no fumador se le permite llevar 50 kg
de peso y al fumador sólo 20 kg.
Función objetivo a maximizar:
Si el autobús tiene 90 plazas y admite
F(x,y) = 100x + 60y un equipaje de hasta 3000 kg,¿cuál debe
ser la oferta de la compañía si se quiere
obtener el máximo beneficio?
Practica con GeoGebra
80

81. 81

82. 82

83. 83

84. 84

85. 85

86. 86

87. EJERCICIO 8:
Restricciones:
Para cubrir un determinado trayecto,
(x=nº vuelos A) una compañía aérea tiene dos aviones:
(y=nº vuelos B) A y B.
0 ≤ x ≤ 120
y≥0 Entre ambos deben hacer, al menos,
60 ≤ x+y ≤ 200 60 vuelos, pero no más de 200;además
y≤x el avión A no puede sobrepasar los 120
vuelos, ni el B puede volar más veces
Consumo a minimizar: que el A.
F(x,y) = 900x+ 700y Si en cada vuelo A consume 900 l.
de combustible y B consume 700 l.,
¿cuántos vuelos debe hacer cada avión
para que el consumo total sea mínimo?
Practica con GeoGebra
87

88. 88

89. 89

90. 90

91. 91

92. 92

93. 93

94. 94

95. 95

96. Restricciones: EJERCICIO 9:
x = nº acciones A Una persona quiere invertir 100 000 €
y = nº acciones B en dos tipos de acciones A y B.
(en decenas de miles de €)
Las de tipo A tienen más riesgo,pero
0≤ x≤6 producen un beneficio del 10 %.
y≥2 Las de tipo B son más seguras,pero
x-y≥0 producen sólo el 7 % nominal.
x + y ≤ 10
Decide invertir como máximo 60 000 €
Beneficio a maximizar: en la compra de acciones A y al menos
20 000 € en la compra de acciones B.
F(x,y) = 0.10x + 0.07y
Además quiere que lo invertido en A
sea por lo menos igual a lo invertido en B.
¿Cómo debe invertir los 100 000 €
para que el beneficio anual sea máximo?
Practica con GeoGebra
96

97. 97

98. 98

99. 99

100. 100

101. 101

102. 102

103. 103

104. 104

105. FIN
© Inmaculada Leiva Tapia I.E.S.Alborán
105