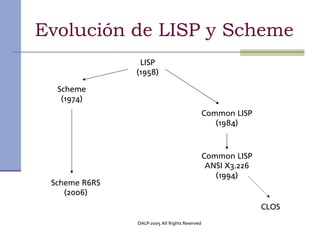
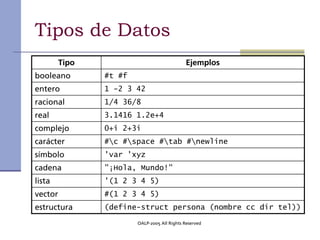
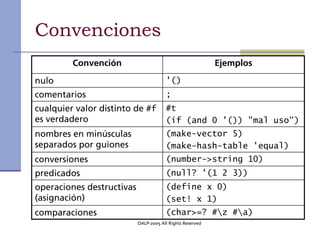
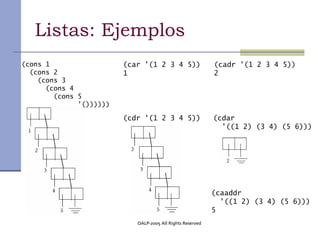
Este documento presenta los conceptos fundamentales de la programación funcional con Scheme. En menos de 3 oraciones, resume que la programación funcional se basa en evaluar funciones matemáticas en lugar de ejecutar instrucciones, Scheme es un lenguaje funcional minimalista basado en Lisp, y presenta conceptos como funciones de orden superior, recursión, currying y listas.