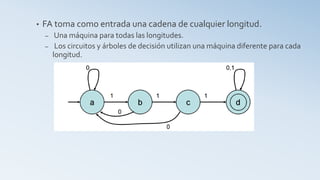
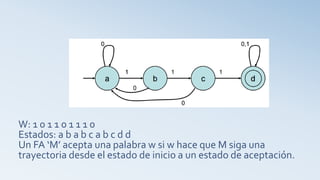
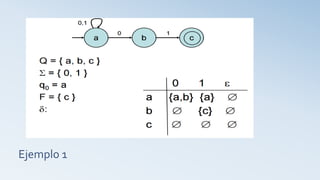
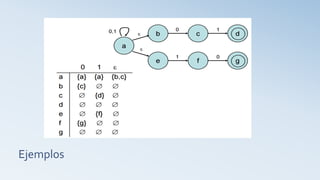
Un autómata finito (AF) es un modelo computacional que procesa cadenas de símbolos para reconocer lenguajes. Se define como una 5-tupla que incluye estados, alfabeto, estado inicial, función de transición y estados de aceptación. Los autómatas finitos no determinísticos permiten múltiples caminos de cálculo para la misma entrada, ampliando así la capacidad de reconocimiento de lenguajes.

1. Autómatas
Finitos
Mariela Bussi Pimentel 16-
0613

2. Autómatas Finitos
• Un autómata finito (AF) o máquina de estado finito es un modelo
computacional que realiza cómputos en forma automática sobre
una entrada para producir una salida.
• Diseñado para:
• - Acepte algunas cadenas de símbolos.
• -Reconocer un lenguaje, que es el conjunto de cadenas que acepta.

3. • FA toma como entrada una cadena de cualquier longitud.
– Una máquina para todas las longitudes.
– Los circuitos y árboles de decisión utilizan una máquina diferente para cada
longitud.

4. W: 1 0 1 1 0 1 1 1 0
Estados: a b a b c a b c d d
Un FA ‘M’ acepta una palabra w si w hace que M siga una
trayectoria desde el estado de inicio a un estado de aceptación.

5. Definición Formal
Formalmente, un autómata finito es una 5-tupla (Q, Σ, 𝑞0, δ, F)
donde:
• Q es un conjunto finito de estados;
• Σ es un alfabeto finito;
• 𝑞0 ∈ Q es el estado inicial;
• δ: Q X Σ es → 𝑄 una función de transición;
• 𝐹 ⊆ 𝑄es un conjunto de estados finales o de aceptación.

6. Cual es la 5-tupla (Q, Σ, 𝑞0, δ, F) ?
Q = { a, b, c, d }
 Σ = { 0, 1 }
δ está dada por el diagrama de estado, o alternativamente
, por una tabla:
 𝑞0= a
F = { d }

7. Definición formal de computación
• Cadena w es aceptada si δ * (𝑞0, w) ∈ F, es decir, w cables del
estado inicial a un estado de aceptación.
• Se rechaza la cadena w si no se acepta.
• Un lenguaje es cualquier conjunto de cadenas sobre alfabeto.
• L (M), lenguaje reconocido por el autómata finito M = {w | w es
aceptado por M}.
• Un lenguaje es regular, o FA-reconocible, si es reconocido por
algún autómata finito.

8. Operaciones lingüísticas
• Operaciones que se pueden utilizar para construir idiomas de otros idiomas.
• Recuperar: Una lengua es cualquier conjunto de cadenas.
• Dado que los idiomas son conjuntos, podemos usar
• Establecer operaciones:
- Unión, L1 ∪ L2
- Intersección, L1 ∩ L2
- Complemento, Lc
- Diferencia de ajuste, L1 - L2
También tenemos nuevas operaciones definidas especialmente para conjuntos de cadenas:
- Concatenación, L1 ◦ L2 o simplemente L1 L2

9. Autómatas finitos no determinísticos
• Generalizar AF mediante la adición de no determinista,
permitiendo que varios cálculos alternativos en la misma cadena de
entrada.
• Las FA determinísticas ordinarias siguen un camino en cada
entrada.
• En un AFND puede darse cualquiera de estos dos casos:
– Que existan transiciones del tipo δ(q,a)=q1 y δ(q,a)=q2, siendo q1 ≠ q2;
– Que existan transiciones del tipo δ(q, ε), siendo q un estado no-final, o bien
un estado final pero con transiciones hacia otros estados.

10. Autómatas finitos no determinísticos
• Formalmente, si bien un autómata finito determinista se define
como una 5-tupla (Q, Σ, q0, δ, F) donde:
• Q es un conjunto finito de estados;
• Σ es un alfabeto;
• 𝑞0 ∈ Q es el estado inicial;
• δ: Q X Σ es → 𝑄 una función de transición;
• 𝐹 ⊆ 𝑄es un conjunto de estados finales o de aceptación.

11. Ejemplo 1

12. Ejemplos

13. Bibliografia
• Nancy Lynch. (2010). Automata, Computability, and Complexity Or,
Great Ideas inTheoretical Computer Science Spring. MIT
OpenCourseWare: MIT.