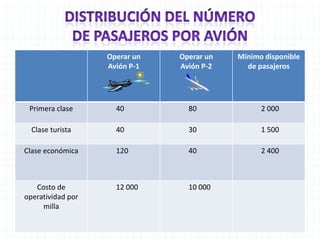
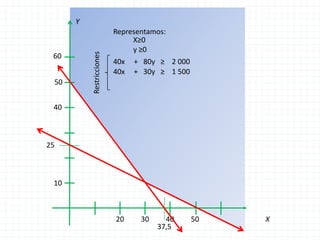
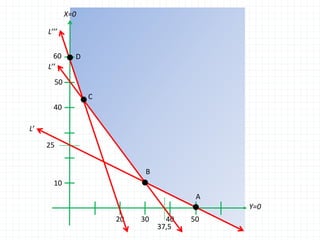
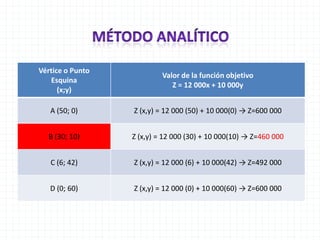
Este documento describe un problema de programación lineal para minimizar los costos de operación de una aerolínea al transportar pasajeros en diferentes clases usando dos tipos de aviones. Se establecen restricciones sobre la capacidad de pasajeros y el costo por milla de cada avión. La solución óptima minimiza la función objetivo de costos totales utilizando una combinación de 37.5 aviones del tipo P-1 y 25 aviones del tipo P-2.

1. UNIVERSIDAD LOS ÁNGELES DE
CHIMBOTE
FACULTAD DE CIENCIAS
CONTABLES, FINANCIERAS Y
ADMINISTRATIVAS
ESCUELA PROFESIONAL DE
ADMINISTRACIÓN
Lic. Madelaine Mautino Minaya

2. La Programación Lineal tiene infinidad de aplicaciones en
la industria, la economía, la estrategia militar y en otras
áreas en las que se presentan situaciones donde se exige
optimizar (maximizar o minimizar) funciones sujetas a
restricciones.
REGION FACTIBLE.- Es la reunión de todas las soluciones factibles.
FUNCIÓN OBJETIVO.- Es una función afín lineal de dos variables de la forma
f(x;y)=ax +by +c ; la que se quiere optimizar; es decir maximizar o minimizar.
SOLUCIÓN FACTIBLE.- Es aquella para la que todas las restricciones se satisfacen.
SOLUCIÓN NO FACTIBLE.- Es una solución para la que al menos una restricción no
Se satisface.
SOLUCIÓN OPTIMA.- Es la que proporciona el valor más favorable de la función
objetivo.

3. Ejemplo
Una aerolínea proveerá servicios para un mínimo de
2000 pasajeros en primera clase 1500 pasajeros en
clase turista y 2400 pasajeros en clase económica.
Operar un avión P-1 cuesta $12000 por milla y puede
transportar 40 pasajeros en primera clase, 40
pasajeros en clase turista y 120 pasajeros en clase
económica. Operar un avión P-2 cuesta $10000 por
milla y puede transportar 80 pasajeros en primera
clase, 30 pasajeros en clase turista y 40 pasajeros en
clase económica. ¿Cuántos aviones de cada tipo se
deberán utilizar para minimizar los costos de
operación?

4. Operar un Operar un Mínimo disponible
Avión P-1 Avión P-2 de pasajeros
Primera clase 40 80 2 000
Clase turista 40 30 1 500
Clase económica 120 40 2 400
Costo de 12 000 10 000
operatividad por
milla

5. Operar un Operar un Mínimo disponible
Avión P-1 Avión P-2 de pasajeros
Primera clase 40x 80y 2 000
Clase turista 40x 30y 1 500
Clase económica 120x 40y 2 400
Costo de 12 000x 10 000y
operatividad por
milla

6. 40x + 80y ≥ 2 000
40x + 30y ≥ 1 500
120x + 40y ≥ 2 400

7. Y
Representamos:
X≥0
y ≥0
Restricciones
60
40x + 80y ≥ 2 000
50
40
25
10
20 30 40 50 X
37,5

8. Y
Representamos:
X≥0
y ≥0
Restricciones
60
40x + 80y ≥ 2 000
40x + 30y ≥ 1 500
50
40
25
10
20 30 40 50 X
37,5

9. Y
Representamos:
X≥0
y ≥0
Restricciones
60
40x + 80y ≥ 2 000
40x + 30y ≥ 1 500
50 120x + 40y ≥ 2 400
40
25
10
20 30 40 50 X
37,5

10. X=0
L’’’
60 D
L’’
50
C
40
L’
25
B
10
A
Y=0
20 30 40 50
37,5

11. Vértice A: 40x + 80y = 2 000 L’
→ {x=50; y=0} → A(50;0)
Y=0
Vértice B: 40x + 80y = 2 000 L’
→ {x=30; y=10} → B(30;10)
40x + 30y = 1 500 L’’
Vértice C: 40x + 30y = 1 500 L’’
→ {x=6; y=42} → C(6;42)
120x + 40y = 2 400 L’’’
Vértice D: 120x + 40y = 2 400 L’’’ → {x=0; y=60} → D(0;60)
x=0

12. Vértice o Punto
Valor de la función objetivo
Esquina
Z = 12 000x + 10 000y
(x;y)
A (50; 0) Z (x,y) = 12 000 (50) + 10 000(0) → Z=600 000
B (30; 10) Z (x,y) = 12 000 (30) + 10 000(10) → Z=460 000
C (6; 42) Z (x,y) = 12 000 (6) + 10 000(42) → Z=492 000
D (0; 60) Z (x,y) = 12 000 (0) + 10 000(60) → Z=600 000