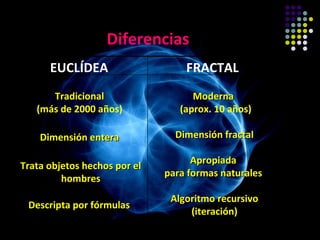
Los fractales son entidades matemáticas que describen formas complejas en la naturaleza mediante la repetición de un proceso geométrico elemental. Fueron acuñados por el matemático Benoit Mandelbrot en los años 1970 para modelar objetos naturales irregulares como montañas, costas y copos de nieve que no se ajustan a la geometría euclidiana tradicional. Los fractales proporcionan una dimensión fractal no entera y algoritmos recursivos para representar estas formas de manera apropiada.

1. LOS FRACTALES
“Las bellezas de las matemáticas”
Alumno: Camila Fuentealba Melgarejo.

2. ¿Qué es un Fractal?
 Los fractales son entidades matemáticas que están por
todas partes.
- Por su variedad, son difíciles de definir porque no todos
cumplen las mismas características, aunque hay algo en
común:
“Son el producto de la repetición de un proceso
geométrico elemental que da lugar a una
estructura final de una complicación
extraordinaria”

3. Etimología de la palabra Fractal
 El matemático francés Benoit Mandelbrot
acuñó la palabra fractal en la década de los
70, derivándola del adjetivo latín "fractus".
El correspondiente verbo latino: frangere,
significa romper, crear fragmentos
irregulares.

4. ¿Porqué Fractales?
- La geometría tradicional, la euclídea, es la rama de la
euclídea
matemática que se encarga de las propiedades y de las
mediciones de elementos tales como puntos, líneas, planos
y volúmenes.
- La geometría euclídea también describe los conjuntos
formados por la reunión de los elementos más arriba
citados, cuyas combinaciones forman figuras o formas
específicas.
…….

5.  …….. Sin embargo, las formas encontradas en la
naturaleza, como montañas, franjas costeras, sistemas
hidrográficos, nubes, hojas, árboles, vegetales, copos de
nieve, y un sinnúmero de otros objetos no son fácilmente
descriptos por la geometría tradicional.
- La geometría fractal provee una descripción y una forma de
modelo matemático para las complicadas formas de la
naturaleza.

6. Diferencias
EUCLÍDEA FRACTAL
Tradicional Moderna
(más de 2000 años) (aprox. 10 años)
Dimensión entera Dimensión fractal
Apropiada
Trata objetos hechos por el
para formas naturales
hombres
Algoritmo recursivo
Descripta por fórmulas
(iteración)

7. Encontramos Fractales en la
naturaleza
 Las formas de la naturaleza son fractales y múltiples procesos
de la misma se rigen por comportamientos fractales. Esto
quiere decir que una nube o una costa pueden definirse por
un modelo matemático fractal que se aproxime
satisfactoriamente al objeto real.
EJEMPLOS DE MODELOS FRACTALES:
LORENZ turbulencias atmosféricas y corrientes marinas.
HENON oscilaciones sufridas por cuerpos celestes que hacen que su
trayectoria no sea completamente elíptica.
CURVAS DE KOCH ALEATORIA fronteras de un país, trazado de una
costa, trazado de un río.
FRACTALES tipo ARBOL sistema arteriales y venosos.

8. Gastón Julia
 Otro precursor de lo que hoy se llama los fractales fue
Gastón julia, recordado sobre todo por lo que hoy es
llamado el Conjunto de Julia o el Set de Julia.
“ Son una familia de
conjuntos fractales que se
obtienen al estudiar el
comportamiento de
los numeros complejos al ser
iterados por una funcion
holomorfa”

9. Algunas imágenes fractales

10. En conclusión las aplicaciones de
los fractales
 Puede parecer que los fractales son meras
curiosidades matemáticas sin ninguna utilidad. Sin
embargo son herramientas de gran potencia para
afrontar el estudio de fenómenos complejos.