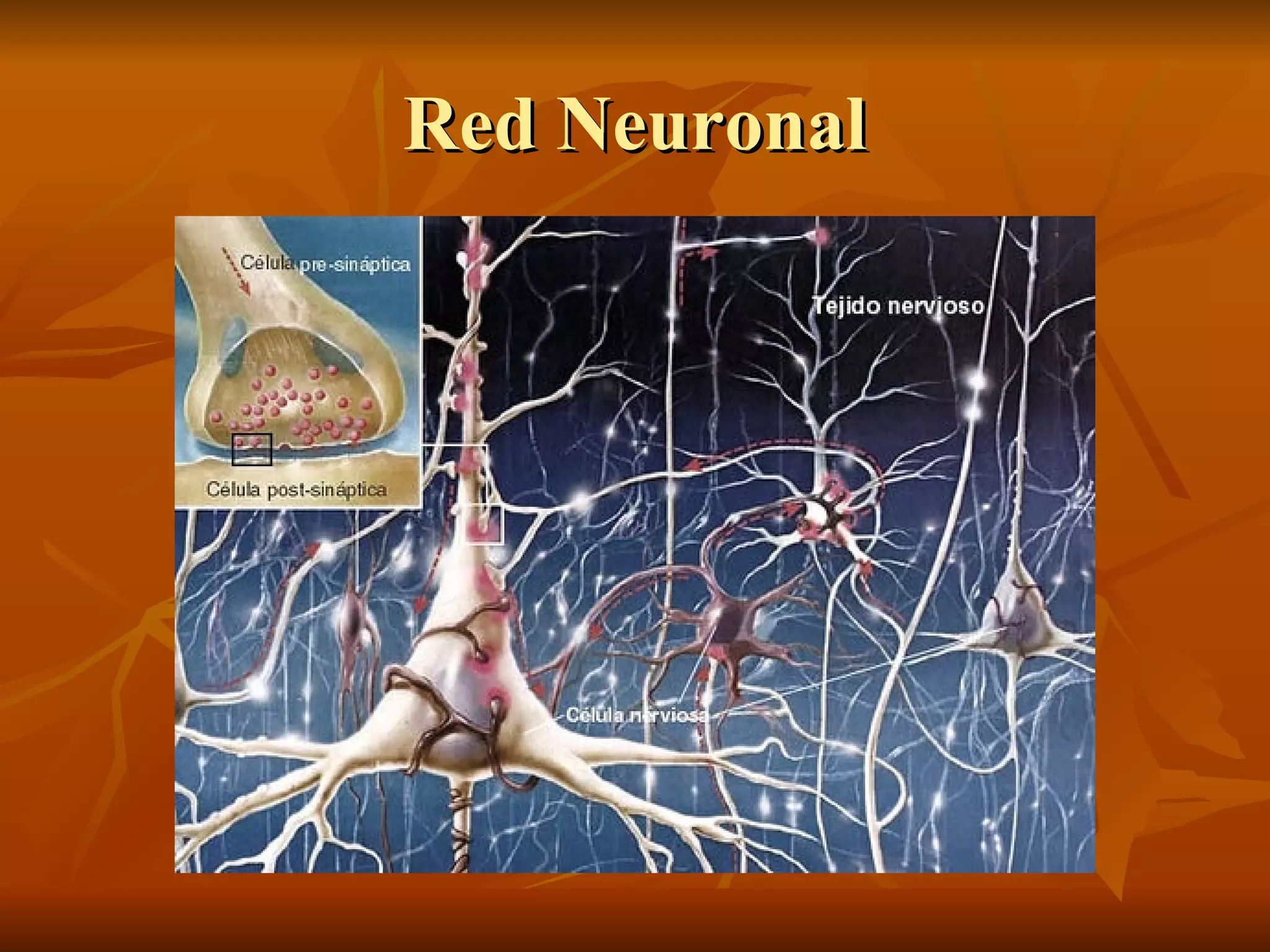
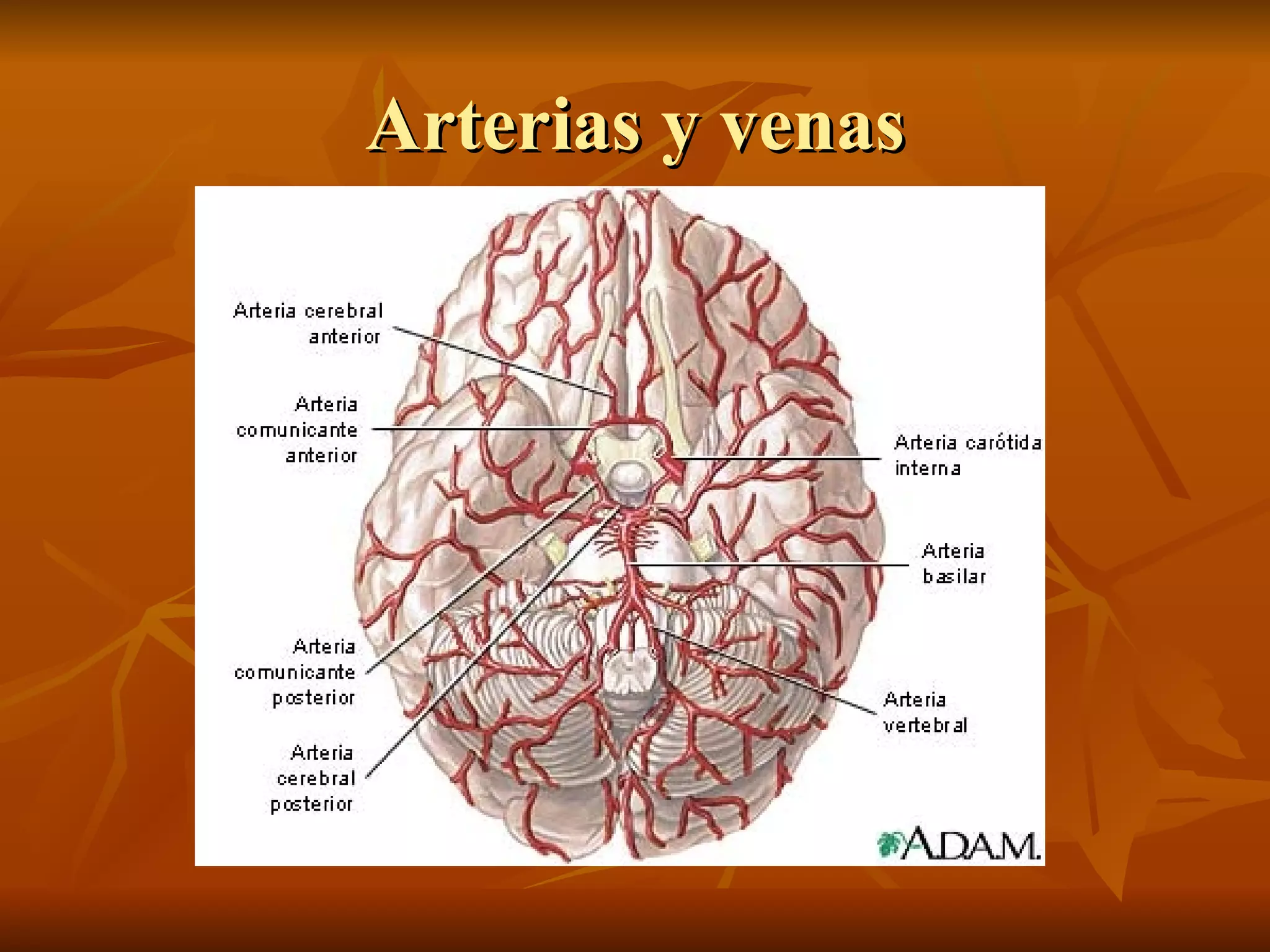
Los fractales son representaciones visuales de ecuaciones matemáticas que describen fenómenos naturales como líneas costeras, formas de plantas y patrones climáticos. Tienen áreas finitas pero perímetros infinitos. El conjunto de Mandelbrot es un fractal formado por círculos concéntricos. Los fractales se generan mediante iteraciones de un patrón geométrico fijo a través de números complejos sometidos a pruebas matemáticas repetidas infinitamente.

1. FRACTALES

2. DEFINICIÓN Los Fractales son las representaciones visuales de las ecuaciones matemáticas, las mismas ecuaciones, de hecho, que describen los fenómenos naturales, tales como líneas de la costa, la forma de las plantas y los patrones climáticos.

3. Estructura y concepción Existen dos características propias a los fractales. Ellas son importantes para comprender su estructura y su concepción. Primero, su Área o Superficie es finita , es decir, tiene límites. Por el contrario y por paradójico que esto resulte, su Perímetro o Longitud es infinita , es decir, no tiene límites. bueno... creo que esto no es muy claro, cierto? Entonces vea usted su primer fractal:

4. Conjunto de Mandelbrot

5. Un fractal también puede ser una serie de circunferencias que se coloquen una sobre el radio de la otra como si fuera su diámetro y así infinitamente.

6. Su nombre deriva de su descubridor y el además considerado padre de la Geometría Fractal, el matemático polaco BENOIT MANDELBROT . (1.975)

7. Características ITERACIÓN. Una iteración es la repetición de "algo" una cantidad "infinita" de veces. Entonces, los fractales se generan a través de iteraciones de un patrón geométrico establecido como fijo, es decir poseen Autosimilitud, invarianza y Dimensión fractal.

8. Dijimos que la Iteración era la repetición constante de un cálculo simple: Los fractales se forman mediante números complejos: (a+bi, A y B nros. Reales; i=unidad imaginaria). Entonces, tenemos el número complejo Z = a+bi, al cual se lo somete a una "prueba matemática". Para ello tomamos el número Z y lo elevamos al cuadrado, sumándoselo después al mismo Z. Luego, elevamos ese resultado y lo elevamos nuevamente al cuadrado, sumándoselo a Z y así infinitamente (iteración). Representemos esto primero en una fórmula y luego en una imagen: ¿Cómo se forman?

10. Copo de Nieve de Koch

11. Un programa de computador asigna un color a cada punto de la imagen basado en las respuestas a una ecuación elegida, con los resultados en formas abstractas fractales.

12. DIFERENCIAS ENTRE LA GEOMETRÍA EUCLÍDEA Y LA FRACTAL EUCLÍDEA FRACTAL Tradicional Moderna (más de 2000 años) (aprox. 30 años) Dimensión entera Dimensión fractal Trata objetos hechos Apropiada para formas por el hombre naturales Descrita por fórmulas Algoritmo recursivo (iteración)

13. Aplicaciones En el caso de las aplicaciones de los fractales, se cuenta, dentro del campo computacional, el proceso de TRANSFORMACIÓN FRACTAL, el que se realiza con imágenes que contienen muchos pixels. Cada uno de estos se va "agrandando", por así decirlo, "infinitamente", sin dejar de ser el mismo. Además, se utilizan para generar efectos en programación y otras cosas tan inusuales (no sé si este sea el concepto adecuado) como la Música Fractal.

14. Otra aplicación se da en el campo de la Geología y Topología. Considerando un litoral cualquiera, con todas sus estrivaciones, se dice que tiende a una longitud infinita, siendo su área finita (características propias de un fractal).

15. Además, Mandelbrot propuso que galaxias y otros cuerpos semejantes se regían por el mismo concepto.

16. El genial Mandelbrot, en su libro "La Geometría Fractal de la Naturaleza", señala parafraseando:"¿Por qué a menudo se describe la geometría como algo frío y árido? Sí, es incapaz de describir la forma de una nube, una montaña, una costa o árbol, porque ni las nubes son esféricas ni las montañas cónicas o un árbol cilíndrico". Pero es la base de toda vida.

17. Y ahora….. ¡A lo que vinimos!

18. Fractales en base a fórmulas matemáticas

41. Fractales en la Artesanía

46. Fractales en Medicina

47. Árbol bronquial

48. Red Neuronal

49. Arterias y venas

50. ¡En los círculos de trigo de Inglaterra!

57. En la naturaleza

75. En el agua…

83. CONCLUSIÓN Alice Kelley dice, “Los Fractales son una mirada intuitiva al Infinito para que se comprenda el mundo natural, además de ser una prueba de que las matemáticas son bellas.” FIN CICLO DE CHARLAS TEMPORADA 2007 MARIA ELENA SARMIENTO