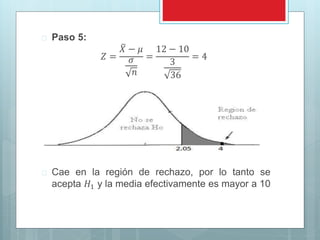
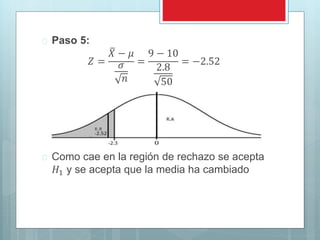
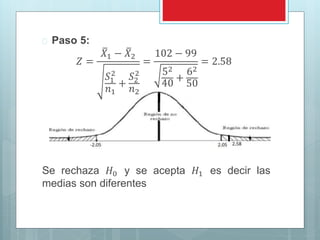
Este documento presenta los conceptos y procedimientos básicos para realizar pruebas de hipótesis estadísticas. Explica los cinco pasos para probar una hipótesis, incluyendo plantear las hipótesis nula y alternativa, seleccionar un nivel de significación, identificar el valor estadístico de prueba, formular una regla de decisión y tomar una muestra para llegar a una conclusión. También cubre temas como pruebas de una y dos colas, pruebas para medias y proporciones poblacional