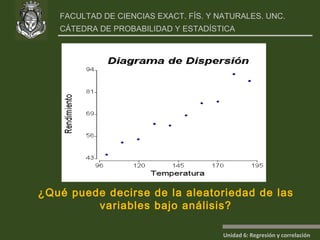
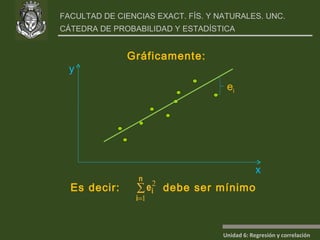
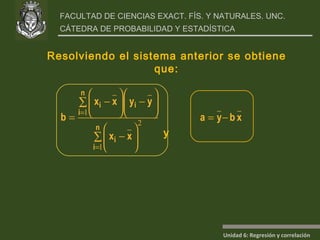
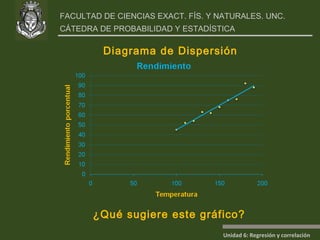
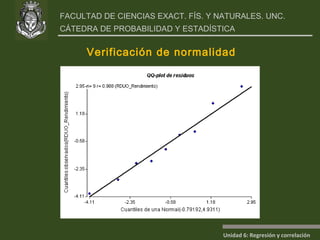
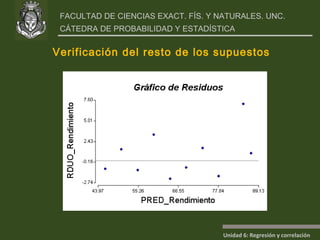
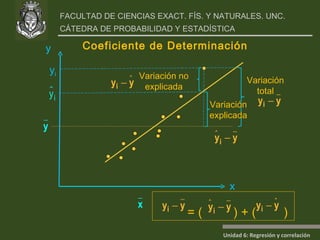
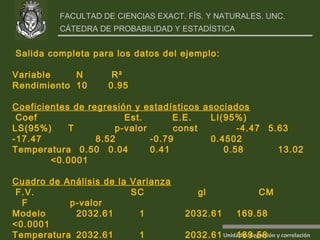
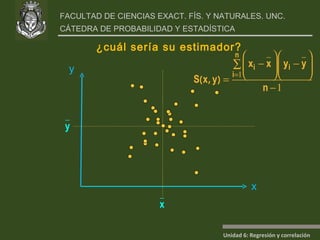
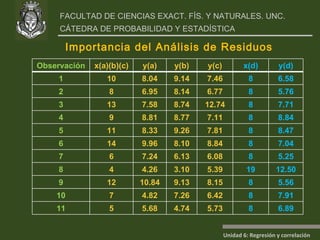
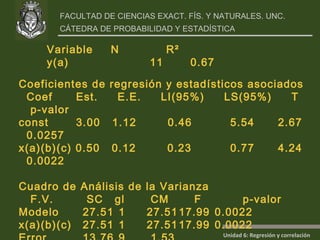
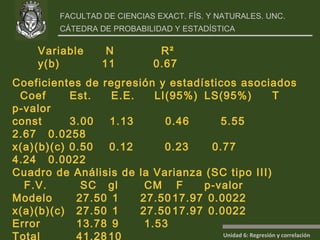
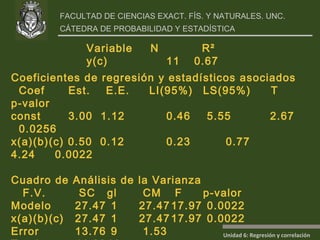
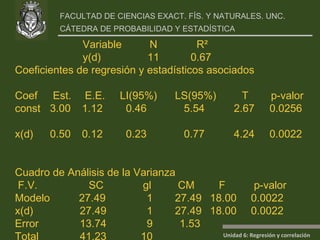
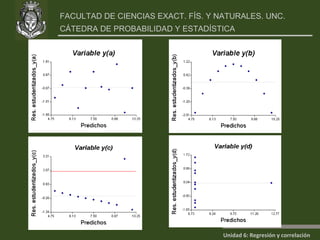
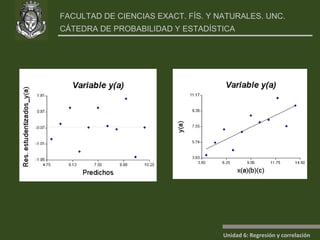
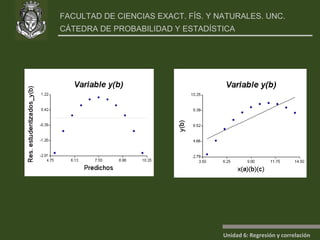
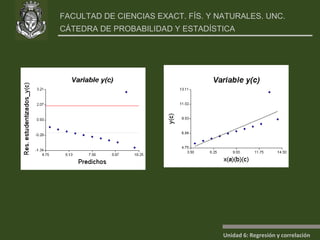
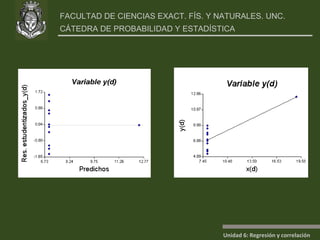
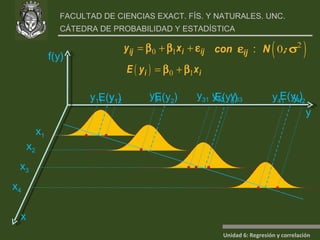
Este documento presenta un análisis de regresión y correlación de datos sobre rendimiento (y) y temperatura (x) de un proceso. Muestra los pasos para estimar la recta de regresión, incluyendo estimar los parámetros a y b, y realizar pruebas de hipótesis. Explica conceptos como coeficiente de determinación, análisis de residuos y validación de supuestos.

1. Análisis de Regresión y Correlación Analicemos el siguiente ejemplo: En un experimento de laboratorio, se desea conocer el rendimiento de un proceso (y), en relación con la temperatura a la que se desarrolla (x). Los datos obtenidos fueron los siguientes: ¿Puede decirse que exista relación entre los valores de x y de y? x 100 110 120 130 140 150 160 170 180 190 y 45 52 54 63 62 68 75 76 92 88

2. ¿Pueden servir los valores de temperatura para predecir los valores de rendimiento ? Si fuera así, ¿qué forma debería tener un gráfico rendimiento - temperatura ?

3. ¿Qué puede decirse de la aleatoriedad de las variables bajo análisis?

4. ¿Qué forma podría tener un modelo que describiera la posible relación entre estas dos variables? Hasta ahora podemos decir que: X es una variable determinística y es intención del análisis de regresión establecer si es explicativa o no. Y es una variable aleatoria de la cuál no sabemos mucho más. Aunque sí, en este caso podríamos pensar que se relaciona de manera lineal con x.

5. f(y) x Y x 1 x 2 x 3 x 4 y 11 y 12 y 21 y 31 y 32 y 33 y 41 y 42 E(Y 1 |x 1 ) E(Y 2 |x 2 ) E(Y 3 |x 3 ) E(Y 4 |x 4 ) Hipótesis y Supuestos

7. ¿Bajo estos supuestos, cuál es la distribución de la variable dependiente para cada valor de x? Recordemos que: Entonces:

8. Habíamos dicho que el objetivo consiste en estimar la mejor recta de regresión que permita describir el comportamiento de la variable explicada (Y) en términos de la explicativa (x). Para ello: ¿qué necesitamos estimar? ¿Qué condición debe cumplir esta recta de modo de lograr la mejor estimación de los valores de la variable explicada?

9. x y e i Gráficamente: Es decir: debe ser mínimo

10. ¿Cómo podemos expresar e i en términos de la información disponible? Entonces deberá minimizarse la expresión: que es lo mismo que: Que habrá que minimizar en a y b, entonces: y

11. Resolviendo el sistema anterior se obtiene que: y

12. Apliquemos lo anterior al ejemplo dado inicialmente. Los datos son: Donde x representa la temperatura a la que se desarrolla un experimento de laboratorio y y el rendimiento porcentual de dicho experimento. ¿Cuál es el primer paso en un análisis de regresión? Hagan!!!!!!!! x 100 110 120 130 140 150 160 170 180 190 y 45 52 54 63 62 68 75 76 92 88

13. ¿Qué sugiere este gráfico? Diagrama de Dispersión

14. ¿Cuál sería el segundo paso? Tienen razón, háganlo Si realizamos la estimación mediante el uso de un software, la salida que entregará será parecida a la siguiente: Coef Est. E.E. LI(95%) LS(95%) T p-valor c onst -4.47 5.63 -17.47 8.52 -0.79 0.45 Temp. 0.50 0.04 0.41 0.58 13.02 <0.0001 ¿Qué indica cada uno de los valores de la tabla anterior? Por lo tanto: y = - 4.47 + 0.50 x ¿tiene sentido el valor de “a” para la situación analizada?

15. Inferencia en la Regresión Lineal Los estimadores de los parámetros son variables aleatorias y los valores obtenidos estimaciones puntuales de los mismos. Para obtener mayor seguridad de que el modelo construido tiene validez, ¿qué recurso podríamos utilizar? Para poder realizarlas, es necesario conocer las distribuciones de los estimadores. ¿Por qué?

16. Prueba de hipótesis para β 1 Distribución de b: donde representa la varianza de los errores en el modelo teórico, por lo tanto resulta necesario estimarla: y ¿Qué propiedades tiene b como estimador?

17. Realicemos la prueba de hipótesis H 0 : H 1 : Estadístico de la prueba: Nivel de significación: según el caso. ¿Por qué?

19. Verificación de normalidad

20. Verificación del resto de los supuestos

21. Coeficiente de Determinación x y Variación total Variación explicada Variación no explicada = ( ) + ( ) y i

22. Esta suma de variaciones tiene una propiedad que permite escribir: o SCT = SCR + SCM y ¿qué indica esta última expresión?

23. Salida completa para los datos del ejemplo: Variable N R² Rendimiento 10 0.95 Coeficientes de regresión y estadísticos asociados Coef Est. E.E. LI(95%) LS(95%) T p-valor const -4.47 5.63 -17.47 8.52 -0.79 0.4502 Temperatura 0.50 0.04 0.41 0.58 13.02 <0.0001 Cuadro de Análisis de la Varianza F.V. SC gl CM F p-valor Modelo 2032.61 1 2032.61 169.58 <0.0001 Temperatura 2032.61 1 2032.61 169.58 <0.0001 Error 95.89 8 11.99 Total 2128.50 9

24. Análisis de Correlación Tiene por objetivo valorar la “fuerza” de la asociación entre las variables Para ello se define una medida de asociación: LA COVARIANZA

25. ¿cuál sería su estimador? y x

26. Si estandarizamos la expresión anterior obtenemos otra medida de asociación, pero relativa Llamada coeficiente de correlación muestral Calculemos estas medidas para el ejemplo dado r = 0.98 (ver prueba de hipótesis para este coeficiente)

27. Importancia del Análisis de Residuos Observación x(a)(b)(c) y(a) y(b) y(c) x(d) y(d) 1 10 8.04 9.14 7.46 8 6.58 2 8 6.95 8.14 6.77 8 5.76 3 13 7.58 8.74 12.74 8 7.71 4 9 8.81 8.77 7.11 8 8.84 5 11 8.33 9.26 7.81 8 8.47 6 14 9.96 8.10 8.84 8 7.04 7 6 7.24 6.13 6.08 8 5.25 8 4 4.26 3.10 5.39 19 12.50 9 12 10.84 9.13 8.15 8 5.56 10 7 4.82 7.26 6.42 8 7.91 11 5 5.68 4.74 5.73 8 6.89

28. Coeficientes de regresión y estadísticos asociados Coef Est. E.E. LI(95%) LS(95%) T p-valor const 3.00 1.12 0.46 5.54 2.67 0.0257 x(a)(b)(c) 0.50 0.12 0.23 0.77 4.24 0.0022 Cuadro de Análisis de la Varianza F.V. SC gl CM F p-valor Modelo 27.51 1 27.51 17.99 0.0022 x(a)(b)(c) 27.51 1 27.51 17.99 0.0022 Error 13.76 9 1.53 Total 41.27 10 Variable N R² y (a) 11 0.67

29. Coeficientes de regresión y estadísticos asociados Coef Est. E.E. LI(95%) LS(95%) T p-valor const 3.00 1.13 0.46 5.55 2.67 0.0258 x(a)(b)(c) 0.50 0.12 0.23 0.77 4.24 0.0022 Cuadro de Análisis de la Varianza (SC tipo III) F.V. SC gl CM F p-valor Modelo 27.50 1 27.50 17.97 0.0022 x(a)(b)(c) 27.50 1 27.50 17.97 0.0022 Error 13.78 9 1.53 Total 41.28 10 Variable N R² y(b) 11 0.67

30. Variable N R² y(c) 11 0.67 Coeficientes de regresión y estadísticos asociados Coef Est. E.E. LI(95%) LS(95%) T p-valor const 3.00 1.12 0.46 5.55 2.67 0.0256 x(a)(b)(c) 0.50 0.12 0.23 0.77 4.24 0.0022 Cuadro de Análisis de la Varianza F.V. SC gl CM F p-valor Modelo 27.47 1 27.47 17.97 0.0022 x(a)(b)(c) 27.47 1 27.47 17.97 0.0022 Error 13.76 9 1.53 Total 41.23 10

31. Coeficientes de regresión y estadísticos asociados Coef Est. E.E. LI(95%) LS(95%) T p-valor const 3.00 1.12 0.46 5.54 2.67 0.0256 x(d) 0.50 0.12 0.23 0.77 4.24 0.0022 Cuadro de Análisis de la Varianza F.V. SC gl CM F p-valor Modelo 27.49 1 27.49 18.00 0.0022 x(d) 27.49 1 27.49 18.00 0.0022 Error 13.74 9 1.53 Total 41.23 10 Variable N R² y(d) 11 0.67

37. f(y) x y x 1 x 2 x 3 x 4 y 11 y 12 y 21 y 31 y 32 y 33 y 41 y 42 E(y 1 ) E(y 2 ) E(y 3 ) E(y 4 )