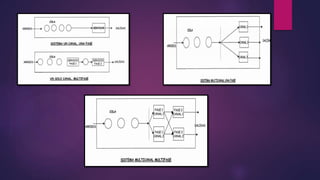
El documento introduce cuatro modelos de simulación de colas comúnmente usados. El Modelo A asume arribos de Poisson y tiempos de servicio exponenciales para un solo canal. El Modelo B considera múltiples canales atendiendo una sola cola. El Modelo C supone tiempos de servicio constantes. Y el Modelo D tiene una población limitada de clientes.

1. SIMULACION DE
COLAS

2. INTRODUCCION
El objetivo de la teoría de colas es modelar sistemas de espera tales
que funcionan de la siguiente manera. Existe un medio al que llegan
clientes demandando cierto servicio. Luego, a consecuencia de que
la demanda no puede ser satisfecha inmediatamente, se forma una
cola (o línea de espera) de clientes en espera de ser atendidos por
el o los servidores correspondientes. Los tiempos entre arribo de
clientes consecutivos al sistema y los tiempos de servicio son
aleatorios, y son representados por variables aleatorias con alguna
distribución de probabilidad.

3. ALCANCE DE LOS MODELOS DE COLAS
Las líneas de espera se presenta, cuando los "clientes" llegan a un "lugar" demandando un servicio a un “servidor", el cual tiene una cierta
capacidad de atención. Si el servidor no está disponible y el cliente decide esperar, entonces se forma la línea de espera. Podemos citar algunas:
 Arribo de clientes a los cajeros de un banco.
 Arribo de automóviles a las estaciones de gasolina.
 Funcionamiento y congestión de las centrales telefónicas.
 Venta de entradas en las ventanillas.
 Reparación de máquinas por los mecánicos.
 Aterrizaje de aviones en un aeropuerto.
 Ejecución de tareas en los centros de cómputo, etc.

4. Los sistemas de espera son modelos de
sistemas que proporcionan servicio. Como
modelo, pueden representar cualquier
sistema en donde los trabajos o clientes
llegan buscando un servicio de algún tipo y
salen después de que dicho servicio haya
sido atendido.Aquí cito algunos ejemplos:

5. ATRIBUTOS A CONSIDERAR EN UN MODELO DE
COLAS
Una cola de espera esta compuesta de tres elementos:
• Arribos o ingresos al sistema
• Disciplina en la cola
• Servicio
Estos tres componentes tienen ciertas características que deben
ser examinadas antes que desarrollar el aspecto matemático de los
modelos de cola.

6.  La fuente de ingreso que genera los Arribos o clientes para el servicio tiene tres características principales: Tamaño de la población que
arriba(limitado o ilimitado), patrón de llegada a la cola, tamaño de la población.
 Una segunda característica de las líneas de espera se refiere a la Disciplina en la cola mediante la cual los clientes reciben el servicio.
La mayoría de los sistemas usan la regla primero en entrar primero en salir (First In First Out).
 La tercera característica de un sistema de colas es el Servicio En él son importantes dos propiedades básicas: La configuración del
sistema de servicio y el patrón de tiempo de servicio.

8. TIPOS DE MODELO DE COLAS
Existe una cantidad enorme de Modelos de Colas que pueden utilizarse. Nos vamos a concentrar en 4 de los modelos más usados.
 Modelo A: Un canal, Arribos según la Distribución de Poisson; Tiempos de Servicio exponenciales
 Modelo B: Multicanal
 Modelo C: Tiempo de Servicio constante
 Modelo D: Población Limitada

9. Modelo A: MODELO DE COLAS DE UN SOLO
CANAL, (MODELO M/M/1):
Asumimos que existen las siguientes condiciones:
1. Los clientes son servidos con una política FIFO y cada arribo espera a ser servido sin importar
la longitud de la línea o cola.
2. Los arribos son independientes de arribos anteriores, pero el promedio de arribos, no cambia
con el tiempo. v
3. Los arribos son descritos mediante la distribución de probabilidad de Poisson y proceden de
una población muy grande o infinita.
4. Los tiempos de servicio varían de cliente a cliente y son independientes entre sí, pero su tasa
promedio en conocida.
5. Los tiempos de servicio se representan mediante la distribución de probabilidad exponencial
negativa.
6. La tasa de servicio es más rápida que la tasa de arribo

13. Dos o más servidores o canales están disponibles para atender a los clientes que arriban. Los clientes forman una sola
cola y se los atiende de acuerdo al servidor que queda libre. Asumimos que los arribos siguen la distribución de
probabilidad de Poisson y los tiempos de servicio son distribuidos exponencialmente.
Los servicios se los hace de acuerdo a la política primero en llegar primero en ser servido (PEPS) y todos los servidores
atienden a la misma tasa.
MODELO B: MODELO DE COLA
MULTICANAL (M/M/S)

15. MODELO C: MODELO DE TIEMPO DE
SERVICIO CONSTANTE (M/B/1)
Algunos sistemas tienen tiempos de servicio constantes en lugar de exponencialmente distribuidos. cuando los clientes son
atendidos o equipos son procesados con un ciclo fijo como es el caso de una lavadora de carros automatizada o ciertos
entretenimientos en los parques de diversiones, el asumir servicio constante es adecuado.

16. MODELO D: MODELO DE POBLACIÓN
LIMITADA.
• Este modelo puede ser usado por ejemplo si estamos considerando reparaciones de equipo en una fábrica que tiene 5 máquinas.
Este modelo permite cualquier número de reparadores a ser considerados.
• La razón por la cual este modelo difiere de los otros tres es que ahora hay una relación de dependencia entre la longitud de la cola
y la tasa de arribo. La situación extrema sería si en la fábrica tenemos 5 máquinas, todas se han dañado y necesitan reparación;
siendo en este caso la tasa de arribo CERO. En general, si la línea de espera crece, la rata de llegada tiende a cero