El documento describe los diferentes conjuntos de números y sus propiedades. Introduce el conjunto de los números reales R como el más grande, que incluye a los números naturales N, enteros Z, racionales Q e irracionales. Explica que R se define como la unión de Q y los irracionales, y que las operaciones de suma y multiplicación en R cumplen con la propiedad de ser cerradas. Además, detalla que las calculadoras pueden representar números reales con hasta 10 cifras decimales, aunque existen programas más precisos.

















![Taller
Evaluación formativa
Evaluación formativa
Taller
20
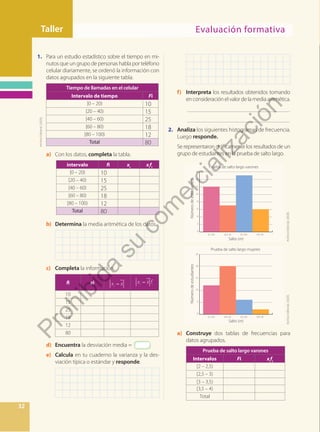
1. Completa los datos de la tabla.
a b a+b (a+b)2
a2
b2
(a2+b2)2
–4 3
2 –5
1
2
4
0 −
2
3
2. Expresa el resultado de la operación como una
sola potencia.
a) (6³ ÷ 6² ) =
_____________________________________
b) (8 –3
)4
=
_____________________________________
c) [(3,5)4
(3,5) 3
]
–2
=
_____________________________________
d)
5
3
3
5
3
2
5
3
5 12
_____________________________________
_____________________________________
3. Escribe en el casillero la letra de la respuesta
correcta perteneciente a cada literal. Observa la
palabra que se forma.
a) [(2)2
]
–1
P. 16
b)
122
15
5 0 3
= T. 2
c) (0,9)15
÷ (0,9)12
E.
1
163
d) [4]2
S. 9
10
3
e)
42
( )
1
16 2
3
O.
5
2
f)
2
5
2
5
2
5
2
× 2 R.
1
4
g) ÷
−
−
−
−
25
5
0,05
0,1
1
2
2
3
E. 1
4. Aplica las propiedades de la potenciación, y es-
cribe (V) si son verdaderas o (F) si son falsas las
siguientes afirmaciones:
a) (32
)8
= 310
b) 312 × 10–6
= 3,12 × 10–4
c) =
−
−
−
10
5
2
a
a
a
2
2
2
d) (0,01)3
= 10–4
5. Resuelve las siguientes expresiones, aplicando
las propiedades de la potenciación.
a)
× × × ×
× ×
− −
−
b.
5 5 125 2 2
2 5 2
6 5 4 5
5 3 6
b)
× + × − ×
×
2 10 3 10 6 10
4 10
4 4 3
8
c)
× + × × ×
× ÷ ×
2 10 7 10 5 10
4 10 2 10
5 4 3
6
d) ( ) ( )
( )
× ÷ × +
× − ×
×
3 10 3 10
3 10 7 10
4 10
3 4 5 2
6 6
3 2
f)
+ + − ×
10 10 10 5 10
10
5 4 3 4
4
=
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-18-320.jpg)


































![55
Una inecuación es
una desigualdad de
dos cantidades, tal
que la una es mayor
que la otra. Los
símbolos , , ≥ y ≤ se
denominan signos de la
desigualdad.
¿Sabías qué?
La ley de tricotomía
dice que si a y b son
dos números reales
cualesquiera, se
cumple solo una de las
siguientes relaciones:
a b, a = b; a b
¿Sabías qué?
Tipos de intervalos
Desigualdades estrictas Desigualdades no estrictas
a b a − b es positiva a ≥ b a b o a = b
a b a − b es negativa a ≤ b a b o a = b
Enunciado Propiedad Ejemplo
Una desigualdad no cambia
de sentido si se suma o se
resta un mismo número a
cada miembro.
Si a b, entonces
a ± c b ± c.
8 10; 8 + 4 10 + 4;
12 14
1 –7; 1 – 5 –7 – 5;
–4 –12
Una desigualdad no cambia
de sentido si se multiplican
o se dividen sus dos
miembros por un mismo
número positivo.
Si a b y c es un número
positivo, entonces ac bc.
c 0
3 7; 3(2) 7(2);
6 14
4 –2, 4(5) –2(5);
20 –10
Una desigualdad cambia
de sentido cuando se
multiplican o se dividen
sus dos miembros por un
número negativo.
Si a b y c es un número
negativo, entonces ac bc.
c 0
–5 2, –5(–3) 2(–3),
15 –6
8 3, 8(–10) 3(–10),
–80 –30
Propiedades de las desigualdades
Intervalo Interpretación Notación Conjunto Representación gráfica
Abierto No incluye los
extremos a y b.
(a, b) o ]a, b[ {x ∈ ℝ / a x b}
Cerrado Sí incluye los
extremos a y b.
[a, b] {x ∈ ℝ / a ≤ x ≤ b}
Semiabierto
por la
izquierda
No incluye el
extremo izquierdo a.
(a, b] o ]a, b] {x ∈ ℝ / a x ≤ b}
Semiabierto
por la derecha
No incluye el
extremo derecho b.
[a, b) o [a, b[ {x ∈ ℝ / a ≤ x b}
Infinito No incluye el
extremo izquierdo
y tiende a +∞.
(a, +∞) o ]a, +∞[ {x ∈ ℝ / x a}
Infinito No incluye el
extremo derecho
y tiende a –∞.
(–∞, a) o ]–∞, a[ {x ∈ ℝ / x a}
Infinito Sí incluye el extremo
izquierdo y tiende
a +∞.
[a, +∞) o [a, +∞[ {x ∈ ℝ / x ≥ a}
Infinito Sí incluye el extremo
derecho y tiende
a –∞.
(–∞, a] o ]–∞, a] {x ∈ ℝ / x ≤ a}
∞
–∞ a b
∞
–∞ a b
∞
–∞ a b
∞
–∞ a b
∞
–∞ a b
∞
–∞ a b
∞
–∞ a b
∞
–∞ a b
Archivo Editorial, (2020).
Archivo Editorial, (2020).
Archivo Editorial, (2020).
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-55-320.jpg)

![57
M.4.1.38. Resolver ecuaciones de primer grado con una incógnita en R para resolver problemas sencillos.
M.4.1.39. Representar un intervalo en R de manera algebraica y gráfica, y reconocer el intervalo como la solución de una
inecuación de primer grado con una incógnita en ℝ.
6. Expresa el intervalo como desigualdad en la
variable x.
a) (–5, 8)
b) (–∞, 3]
c) [4, ∞)
d) [–7, 12]
e) [0, 8)
f) (1, 6]
7. Escribe el intervalo que está representado en la
recta numérica.
8. Determina qué números enteros se encuentran
en cada intervalo.
Trabajo colaborativo
Actividad indagatoria
Trabajen en equipo y resuelvan.
9. Resuelvan los siguientes problemas:
a) El doble de un número aumentado en 3 es
igual al triple de dicho número disminuido
en 5.
b) El triple de la edad de María aumentada
en 5 años es igual al doble de su edad
aumentada en 10.
10. Dado –3 4, determinen la desigualdad obte-
nida si:
a) Se suma 5 a ambos lados.
b) Se resta 2 a ambos lados.
c) Ambos lados se multiplican por 3.
d) Ambos lados se multiplican por 1
3
.
11. Representen gráficamente.
a) (–∞, 3]
b) (2, ∞)
c) [3, 6]
d) (3, 7)
12. Resuelvan las siguientes inecuaciones:
a) –3 x – 1 ≤ 5
b) 1
2
x + 3 ≤ 3
4
x – 2
c) 5x + 2 x – 3 4x – 5
d) 5 – 3x
2
– x – 1 ≥
+ x
3
4
1
2
e) 3x+0,61,2x–1x+3,4
f) 2 + x + 3
4
x + 2 ≤ 5(x – 4)
2
13. Indaga y escribe en tu cuaderno.
¿Cuándo una ecuación es incompatible?
a)
–4 4
b)
–3 7
c)
–9 1
d)
4
e)
a) (– 2, 2 )
b) – ,
c) (–2π, π)
7
2
1
2
) )
d) [0,3; 5[
–3 3
–6
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-57-320.jpg)











![69
M.4.2.1. Definir y reconocer proposiciones simples a las que se puede asignar un valor de verdad para relacionarlas entre sí con
conectivos lógicos: negación, disyunción, conjunción, condicionante y bicondicionante; y formar proposiciones compuestas.
5. Realiza la tabla de verdad de las siguientes expre-
siones:
a) p q p
( )
∨ ∧
b) p q r r
( )
[ ]
∨ ∧ ∨
c) r p q p
[ ]
( )
∧ ∧ ∧
6. Encuentra el valor de verdad de las siguientes pro-
posiciones compuestas sin usar tablas de verdad.
a) –2elevadoalcuadradodaunnúmeropositivo
y da un número par.
p: ___________________________________
q: ___________________________________
p q
Trabajo colaborativo
Actividad indagatoria
7. Trabajen en equipo y resuelvan.
Escriban en lenguaje común, utilizando los
conectores lógicos. Interpreten y expresen
verbalmente.
a) Sean p: Carla es deportista y q: Carla es
bailarina.
p q p v q (p q) v q
b) Sean p: Miguel viaja a México y q: Miguel
viaja a Colombia.
p q p v q (p v q) q
c) Sean p: Estudio matemática, q: Estudio
inglés.
p r q v r (p v q) r
8. Realicen las siguientes operaciones.
a) r p r q
p r q r
r q p
p p r q
[( ) ]
( ) ( )
( )
( )
∧ ∨ ∧
∨ ∧ ∨
∧ ∨
∨ ∧ ∧
b)
c)
d)
9. Indaga en qué consiste la disyunción inclusiva
y escribe dos ejemplos.
10. Indaga acerca de otros conectores lógicos
y escribe dos ejemplos de proposiciones com-
puestas que utilicen dichos conectores.
p q (p v q) p (p v q) p
V V
V F
F V
F F
p q r (q r) [p v (q r)] [p v (q r)] v r
V V V
V V F
V F V
V F F
F V V
F V F
F F V
F F F
p q r [(r p) [(r p) q] [(r p) q] p
V V V
V V F
V F V
V F F
F V V
F V F
F F V
F F F
b) Diego cocina sopa y prepara arroz o cocina
sopa o prepara arroz.
p: ___________________________________
q: ___________________________________
p q p q
( ) ( )
∧ ∨ ∨
v
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-69-320.jpg)

![71
Ejemplo 3
Sea el siguiente enunciado:“Carlos nació en 1993”.
La proposición es:
p: Carlos nació en 1993, ~ p: Carlos no nació en 1993.
Su tabla de verdad es:
Solución
El valor de p: V significa que Carlos nació en 1993, y
p: F significa que no nació en ese año.
Tautología. Es una proposición compuesta que es cierta para todos los
valores de verdad de sus proposiciones, es decir, su valor de verdad depende
de las relaciones establecidas entre las proposiciones.
Tautología. Es una proposición compuesta que es cierta para todos los
valores de verdad de sus proposiciones, es decir, su valor de verdad depende
de las relaciones establecidas entre las proposiciones.
Ejemplo 4
Construir la tabla de verdad de: p q p p q
( ) ( )
∧ ∧ → ∨
Solución
• Identificamos el conectivo principal ( ) para establecer el resultado final.
• Determinamos la cantidad de proposiciones, en este caso (p, q).
La tabla de verdad tendrá 2n
= 22
= 4 filas.
• Resolvemos aplicando el siguiente orden:
p q [(p q) p] (p v q)
V V V V V V V
V F F F V V V
F V F F F V V
F F F F F V F
Contradicción. Es una proposición compuesta si en todos los casos posibles
de su columna principal su valor de verdad es falso.
Contradicción. Es una proposición compuesta si en todos los casos posibles
de su columna principal su valor de verdad es falso.
Negación ( ). Su función es negar la proposición. Sea p una proposición, la
negación de p es la proposición ~ p, que se lee“no p”, lo que cambia el valor de
verdad de la proposición.
Negación ( ). Su función es negar la proposición. Sea p una proposición, la
negación de p es la proposición ~ p, que se lee“no p”, lo que cambia el valor de
verdad de la proposición.
p ~ p
V F
F V
Una tabla de verdad
que tiene valores
verdaderos y falsos
en su columna
principal se denomina
contingencia.
Recuerda que...
Matemática con
programación
El sistema binario ha
sido utilizado desde
la Antigüedad hasta
nuestros días. Hoy
se utilizan circuitos
lógicos aplicando lógica
matemática. Los valores
de verdad V y F pueden
ser reemplazados por
los valores binarios 1 y
0, respectivamente. Este
sistema ha permitido
programar todo tipo de
aparatos electrónicos
como computadoras o
smartphones.
Conexiones
Como la columna principal tiene solo valores verdaderos, es una tautología.
1. Conjunción
2. Valores de p
3. Conjunción
4. Disyunción
5. Condicional
1 3 2 5 4
Shutterstock,
(2020).
594829253
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-71-320.jpg)
![Taller
Evaluación formativa
Evaluación formativa
Taller
72
1. Expresa simbólicamente las siguientes proposi-
ciones.
a) No es el caso que estudies licenciatura y
arquitectura.
_____________________________________
b) Samsung es una marca de celulares o es una
marca de televisores.
_____________________________________
c) Si Óscar realiza una recarga electrónica, en-
tonces podrá realizar llamadas.
_____________________________________
d) Si no tienes el pasaporte vigente, entonces no
podrás viajar.
_____________________________________
e) Si Mateo no aprueba o no resuelve este pro-
blema, entonces es falso que haya estudiado
o que domine la deducción lógica.
_____________________________________
2. Niega verbalmente cada afirmación.
a) No es cierto que –5 es mayor que –3.
_____________________________________
b) Postulé a una maestría en Ciencias.
_____________________________________
c) No es cierto que 4 sea un número primo.
_____________________________________
d) Yahoo es un buscador de información.
_____________________________________
e) La mandarina es una fruta de la Costa.
_____________________________________
3. Encuentra los valores de verdad correspondientes
para que se cumpla el valor indicado.
a) P q c) p q
V V
b) ~ p ~ q d) p q
F V
4. Realiza la tabla de verdad de las siguientes
fórmulas lógicas. Escribe si es tautología, contra-
dicción o contingencia.
a) p p q p
Es una
b) p q p r q r
Es una
c) (p q) p q
Es una
P q [ p (p q)] ~p
V V
V F
F V
F F
P q ( p q) ~(p q)]
V V
V F
F V
F F
P q r [ (p q) v (p r)] q ~r
V V V
V V F
V F V
V F F
F V V
F V F
F F V
F F F
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-72-320.jpg)
![73
Trabajo colaborativo
7. Trabajen en equipo y resuelvan.
Evalúen las siguientes fórmulas lógicas y com-
paren sus resultados.
a) p q
( ) q p
p p q
( ) p q
( )
p q
( ) p q p
( )
p q p q
( ) r s
( ) r
{ }
b)
c)
d)
M.4.2.1. Definir y reconocer proposiciones simples a las que se puede asignar un valor de verdad para relacionarlas entre sí con
conectivos lógicos: negación, disyunción, conjunción, condicionante y bicondicionante; y formar proposiciones compuestas.
M.4.2.2. Definir y reconocer una tautología para la construcción de tablas de verdad.
5. Halla los valores de verdad de las siguientes
fórmulas lógicas.
a) p q
( ) r r q
( ) si los valores de verdad
de las proposiciones p, q y r son V V F, respec-
tivamente.
p q
( ) r r q
( )
V V F V
V F V
F V
La fórmula lógica es verdadera.
b) (p q) r
[ ] p r s
( ) si los valores
de verdad de las proposiciones p, q, r y s son
F V V F, respectivamente.
c) p q
( ) s r s
[ ] si los valores de
verdad de las proposiciones p, q, r y s son V F F
V, respectivamente.
d)
q r p q
( ) ( )
∨ → ∧ si los valores de p, q y r
son F V F, respectivamente.
Actividad indagatoria
8. Indaga y resuelve.
Un letrero aparece en la entrada a un concier-
to.“Para ingresar, las personas deben presentar
su boleto y ser mayores de edad, o bien estar
acompañadas de una persona adulta”. Repre-
senta el enunciado mediante una fórmula
lógica y evalúa la tabla para identificar los ca-
sos en los que una persona no podrá entrar al
concierto.
6. Evalúa estas proposiciones:
a) Sitepreparasparatriunfar,entoncestriunfarás.
Sin embargo, no te preparas para triunfar.
b) Si mi archivo no abre, entonces volveré a mi
casa y mandaré la información por correo.
c) Volveré a mi casa y mandaré la información
por correo porque mi archivo no abre.
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-73-320.jpg)
![Ley Símbolos
De equivalencia p ⇔p
De Idempotencia p∨p ⇔p p∧p ⇔p
Asociativa
p∨q∨r ⇔ p∨q
( )∨r ⇔p∨ q∨r
( )
p∧q∧r ⇔ p∧q
( )∧r ⇔p∧ q∧r
( )
Conmutativa p∧q ⇔q∧p p∨q ⇔q∨p
Distributiva
p q r
( ) p q
( ) p r
( )
p q r
( ) p q
( ) p r
( )
De identidad
p F F p V p
p F p p V V
De complemento
p p F p p V
p
( ) p F V
V F
De Morgan
p q
( ) p q
p q
( ) p q
De absorción
p p q
( ) p
p p q
( ) p
Condicional simple
p q p q
p q q q
Bicondicional p q p q
( ) q p
( )
Visita el siguiente
enlace para conocer
más del temas.
bit.ly/2T6qEs3
Enlace web
74
Leyes de la lógica proposicional
Tema 6
Son equivalencias lógicas que nos permiten reducir fórmulas lógicas complejas
y expresarlas en forma más sencilla. Las leyes del álgebra proposicional son:
Leyes del álgebra proposicional
Para simplificar
una formula lógica,
podemos seguir estos
pasos:
1. Analizar e identificar
conectores
condicional
y bicondicional,
y entonces aplicar
las respectivas leyes.
2. Asociar términos
para poder aplicar
las leyes del álgebra
proposicional.
Recuerda que...
¿Cuándo son verdaderas la disyunción y la conjunción?
Saberes previos
_________________________________________________________________
≅: Igual a
: Equivale
Simbologíamatemática
Archivo Editorial, (2020).
( ) ociativa
∼ ∼ ∼ ∼
∼ ∼ ∼ ∼
∼ ∼ ∼
∼ ∼ ∼ ∼
( )
( )
[ ]
∨ ∨
≅ ∨ ∨
≅ ∨
≅ ∧
≅ ∧
p q q
p q q
p q
p q
p q
( )
As
De idempotencia
( ) De Morgan
De complemento
( ) ociativa
∼ ∼ ∼ ∼
∼ ∼ ∼ ∼
∼ ∼ ∼
∼ ∼ ∼ ∼
( )
( )
[ ]
∨ ∨
≅ ∨ ∨
≅ ∨
≅ ∧
≅ ∧
p q q
p q q
p q
p q
p q
( )
As
De idempotencia
( ) De Morgan
De complemento
Ejemplo 1
Usando el álgebra de proposiciones, simplifica la proposición.
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-74-320.jpg)
![75
Ejemplo 2
Simplifica a una fórmula lógica más sencilla, utilizando las leyes de la lógica
proposicional.
p q q p
( ) ( )
∧ ∧ ∧
( ) ( )
( )
≅ ∧ ∧ ∧
≅ ∧ ∧
≅ ∧
≅
p q q q
p p F
p F
F
Ejemplo 3
Simplifica la expresión aplicando las leyes de proposiciones.
p q
( ) q p
( ) p q
( )
p q
( ) q p
( ) p q
( )
(p q) q p
( ) p q
( )
(p q) q p
( ) p q
( )
( p q) q p
( ) p q
( )
(q p) p q
( ) p q
( )
(q p) p
[ ] q p q
( )
( p q) p q
( )
(q p) q p
( )
q ( p p)
q F
q
De Morgan
Condicional
De Morgan
Conmutativa
Asociativa
De absorción
Conmutativa
Distributiva
De complemento
De identidad
Condicional
Ejemplo 4
p q
( ) q
p q
( ) q
[ p q
( ) q] [ q p q
( )]
p q
( ) q q
( ) p q
( )
(p q) q
[ ] q q p
[ ]
q (q q) p
[ ]
q q p
[ ]
q q
( ) ( q p)
F ( q p)
V V V
Condicional
Bicondicional
Condicional
De Morgan
De absorción y asociativa
De idempotencia
Distributiva
De complemento
Distributiva y de identidad
George Boole y
Augustus De Morgan,
a mediados del siglo
XIX, presentaron un
novedoso sistema
matemático para
modelar operaciones
lógicas. Obtuvieron una
herramienta apropiada
para la investigación de
los fundamentos de la
matemática.
¿Sabías qué?
George Boole.
Augustus De Morgan.
Wikimedia
Commons,
(2020).
www.wikipedia.org
Asociativa
De complemento
De idempotencia
De identidad
Ingresa al siguiente
enlace web:
bit.ly/2yBvlAW
Imprime y resuelve
ejercicios de lógica
proposicional.
Me refuerzo
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-75-320.jpg)

![77
M.4.2.3. Conocer y aplicar las leyes de la lógica proposicional en la solución de problemas.
f) p q
( ) q p
g) p q
( ) q q
h) p q
( ) p
5. Encuentra el error en el ejercicio y corrígelo.
q p
( ) p
(q p) p p (q p)
Bicondicional
(q p) p p (q p)
Bicondicional
( q p) p ( p p) q
De Morgan
p ( p q)
Idempotencia y absorción
p ( p q)
De Morgan
p (p q)
De Morgan
V q V
Identidad
Trabajo colaborativo
Trabajen en equipo y resuelvan.
6. Escriban la ley que se aplicó en cada paso.
a) p q
( ) r r
( ) q
p q
( ) F q
p q
( ) F q
p q
( ) F q
p q
( ) q
q
__________________________________
b) p q
( ) p q
( ) p q
( )
p (q q)
[ ] p q
( )
p V
[ ] p q
( )
p p q
( )
(p p) q
V q
V
__________________________________
7. Simplifiquen las siguientes fórmulas lógicas.
a)
( )
∨ ∧ ∨ ∨ =
p p p q q
( )
__________________________________
b) ( )
∧ ∧ ∨ ∨ =
p q p q p
( ) )
__________________________________
Actividad indagatoria
8. Indaga y resuelve.
p q
( ) q q
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-77-320.jpg)





![83
7. Indica si los valores propuestos para las incógni-
tas son solución de cada una de las ecuaciones:
a) x = 3 para 2x + 1 = 7
b) x = 2 para 3x + 5x = 4x + 6
c) x = 7 para 3x – 3 (1 − 2x) = − 29 + (2x − 3)
8. Resuelve la siguiente ecuación:
2x – [6 – 2(5x – 4)] = 6x – 2
9. Representa gráficamente la solución del sistema:
y = x +2
y −3x = 4
⎧
⎨
⎪
⎩
⎪
10. Resuelve el siguiente sistema de ecuaciones:
−35x +24y = −57
−4x +9y = 6
⎧
⎨
⎪
⎩
⎪
11. Resuelve la siguiente inecuación y representa el
intervalo:
( )
− + +
x x x
2 2 3 4 6
12. Resuelve el siguiente sistema de inecuaciones
en forma gráfica:
x + y 10
x − y ≥ 6
⎧
⎨
⎪
⎩
⎪
13. Realiza una tabla de verdad de la siguiente
proposición compuesta y analiza la respuesta:
(¬ p v q) ↔ (p → q)
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-83-320.jpg)



![Evaluaciones estandarizadas
87
1. Lee y analiza.
Calcula y: y – 5 = 3y – 25
Argumenta la respuesta:
Escoge la respuesta correcta.
a) y = 10 c) y =
15
2
b) y = –10 d) y = –
15
2
2. Lee y analiza.
Calcula x:
30x – (–x +6) +(–5x + 4) = –(–5x + 6) + (–8 + 3x)
Argumenta la respuesta:
Escoge la respuesta correcta.
a) x = –
8
9
c) x = –
2
3
b) x =
8
9
d) x =
2
3
3. Lee y analiza.
Resuelve: x + 3(x – 1) – 6 + 4(2x + 3) = 0
Argumenta la respuesta:
Escoge la respuesta correcta.
a) x = –
3
4
c) x = –
1
4
b) x =
3
4
d) x =
1
4
4. Lee y analiza.
La suma de dos números es 108 y el doble del
mayor excede al triple del menor en 156. Halla
los números.
Argumenta la respuesta:
Escoge la respuesta correcta.
a) 74,4 y 33,6 c) 52,8 y 55,2
b) 96 y 12 d) 90 y 18
5. Lee y analiza.
La edad de A es triple que la de B y hace 5 años era
el cuádruplo de la de B. Halla las edades actuales:
Argumenta la respuesta:
Escoge la respuesta correcta.
a) 5 y 15 c) 20 y 60
b) 10 y 30 d) 15 y 45
6. Lee y analiza.
Encuentra el intervalo de:
5x – 1 ≥ 8 + 2x
Argumenta la respuesta:
Escoge la respuesta correcta.
a) S1 = (3, –∞) c) S1 = [3, +∞)
b) S1 = (–∞, 3] d) S1 = (–∞, 3)
P
r
o
h
i
b
i
d
a
s
u
c
o
m
e
r
c
i
a
l
i
z
a
c
i
ó
n](https://image.slidesharecdn.com/textointegrado10m0-230123040703-e73e2667/85/texto-integrado-10m0-pdf-87-320.jpg)



