Este documento presenta un resumen de los temas tratados en el libro "Tópicos de Cálculo Volumen II". El libro abarca los siguientes temas: integral indefinida, integral definida, integrales impropias, aplicaciones de la integral definida, coordenadas polares, rectas y planos en el espacio tridimensional y superficies.









![TÓPICOS DE CÁLCULO - VOLUMEN II
Ejemplo 3. Como d (x ln x - x ) = ln x dx, por la obs. 2-iv , se deduce:
J d ( x l n x — x ) = J n x dx = x l n x - x + C
, , í 1 x
Ejem plo 4. J - ^ —j = - arc ta n -+ C , pues
n x ' 1
(-a r c ta n - + C) = -
1
__ 2__
X^
1 +=r4
1
4 + x 2
1.2 P R O P I E D A D E S D E L A I N T E G R A L I N D E F I N I D A
P rop osició n 2. Si / y g son funciones que admiten antiderivadas en el intervalo /
y k es una constante cualquiera, entonces las funciones / ± g y k f admiten
antiderivadas en / y se tiene:
a) [ íf (x ) ± g ( x ) ] d x = J f ( x ) d x ± J g (x )d x
b) I [k f(x )]d x = k j f ( x ) d x
D em o stració n
a) Com o | J [/ (x ) ± 5 (x )]d x j = / (x ) ± ^ (x ) = / (x )d x j ± J g ( x ) dx ,
entonces J [f(x) ± g ( x ) ] d x y J f ( x ) d x ± J g(x)dx son las antiderivadas
de / ( x ) ± g ( x ) . Por tanto,
j [ / ( * ) ± 9 (x)]dx = J f ( x ) d x ± j g ( x )d x
b) L a dem ostración queda com o ejercicio para el lector.
D e la parte (a) se deduce que la integral indefinida de una sum a algebraica de
varias funciones es igual a la sum a algebraica de sus integrales.
E je m p lo 5. Calcule j (e x - 4 x 3 + ln x )d x .
Solución. E n virtud de la proposición 2 y de los ejemplos 1, 2 y 3 se obtiene:
J (e x - 4 x 3 + ln x ) d x = J e xdx - J 4 x 3dx + J l n x d x
= ( ex + Ct ) - ( x 4 + C2) + ( x l n x - x + C3)
= e x - x 4 + x In x - x + C, d on d e C = Cx + C2 + C3
En lo que sigue solamente usarem os una constante única de integración para la
sum a de 2 o m ás funciones.
4
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-11-320.jpg)

![■h
■ h
du
+ u- a
TOPICOS DE CALCULO - VOLUMEN II
1 U
arctan —+ C , (a > 0)
1 u —a
= — ln
2a u + a
1 u + a
= — ln
2a u - a
+ C , (a > 0)
+ C , (a > 0)
26
f du u
—= = = arcsen - + C , (a > 0)
-a rc se c ------1- C , (a > 0)
a
29
30
a rc se n - + C , (a > 0)
a j
f du i ,-----------1
27. I - p = = In u + V u 2 ± a 2 + C
v u 2 ± a 2
r du 1
28. — ;..= -
J u v u 2 — a 2 a
. J yja2 — u 2du = —juVa 2 - u2 + a
j yj'u2 + a 2du = - |u%/u2 + a 2 4- a 2 ln (u + J u 2 + a 2)j 4- C
31. J yju2 - a 2du = - [u v u 2 - a 2 - a 2 ln |u + V u 2 - a 2j] + C
Cada una de éstas fórm ulas se pueden verificar mediante la derivación (respecto a
la variable u).
Por ejemplo, en el caso de la fórm ula 24 se tiene:
dd / 1 iu —ai 1
du 2 a n lu + aU 2a
(ln|u - a - ln|u + a|)
¡L UU
1 1 1 1
2a u - a u + a
P or tanto
f du 1 iu - ai
■ I —^------j = t;—ln --------- + C
J u'- — a 2 2a lu + al
En el caso de la fórm ula 18, se tiene:
d s e n h u
— (In cosh u|) = — —— .?= tanh u
du cosh u
De lo a n te rio r se deduce que J tanh u d u = ln|cosh u| + C.
6
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-13-320.jpg)

![/
TOPICOS DE CALCULO - VOLUMEN II
dx
Ejemplo 9. Calcule ,
J se nh 2x cosh-x
Solución
1 cosh2x - senh2x
Como -----—----—— = -----------—---------—— = csch^x - sech2x, entonces
se n rrx cosh -x senh2x cosh^x
/ se n h 2x c o sh 2x = / CSCh2* dx ~ / Sech2* dx = ~ COth X “ tanh x + C
r x 2 + 2
Ejem plo 10. Encuentre ■ --------dx.
J x 2(x2 + 4)
Solución
Expresando el num erador del integrando en términos de los factores del
denominador, resulta
2 1
+ 2 = x z + - (x z + 4 - x 2) = - [(x 2 + 4) + x z]
Ahora, escribim os la integral como la sum a de dos integrales (haciendo las
sim plificaciones en cada integrando) y obtenemos
í * ¿ + 2 l f i ! + ( i 2 + 4 ) i r dx 1 r dx
J x 2( x 2 + 4 ) X ~ 2 j x 2( x 2 + 4 ) 2 J x 2"+~4 + 2 J x 2^
1 rl 1
~ 2 l2 í
i ri x
: arctan -
+ 2
1 X 1
-a r c ta n - - — + C
4 2 2x
í x 2 —5
Ejem plo 11. Halle / = — —— — dx
J x 2(x 2 - 9)
Solución
Procediendo del m ism o m odo que en el ejemplo anterior, resulta
x 2 — 5 = x 2 + | ( x 2 - 9 - x 2) = | ( x 2 - 9) i- -”X 2
9 9 9
_ f í * 2 + | ( * 2 - 9 ) 4 r dx 5 r dx
J x 2( x z - 9) d x - 9 j x 2 - 9 + 9 j I 2
4 1
= 9 ' ¿ ln
x + 3
x —3
5 2 ix + 3| 5
~ 9 x + ° ~ 2 7 lnL —31 ~ 9 x + C
8
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-15-320.jpg)

![TÓPICOS DE CÁLCULO - VOLUMEN II
f dx
Ejem plo 14. Calcule I — —
Solución
U sando la identidad de la observación 3, se tiene
(■ dx _ 1 f r 1 1
J x 4 —9 ~ ~ 6 J ix 2 + 3 + 3~—~}
111 * 1
- — a rc ta n — + — — ln
6 LV3 V3 2V3
x 2 + 13
dx
+ V 3
- V 3
+ C
f x + 13
Ejem plo 15. Encuentre - -- dx.
J V F T 9
Solución
Trabajando de manera adecuada en el numerador del integrando, se obtiene
f x 2 + 13 , f ( x 2 + 9 ) + 4 f r—------ f dx
. dx = — — dx = yjx2 + 9 dx + 4 1
J V x 2 + 9 J V x 2 + 9 J J V * 2 + 9
= - j * V * 2 + 9 + 9 ln (x + yjx2 + 9 )] + 4 ln (x + j x 2 + 9) + C
= 2 [ W * 2 + 9 + 17 ln (x + J x 2 + 9)] + C
1.4 M ÉTO DOS DE INTEGRACIÓN
Antes de presentar los métodos de integración “por sustitución o cam bio de
variable” y “por partes”, es necesario hacer notar una diferencia esencial entre las
operaciones de derivación y de integración. Dada una función elemental (función
que se obtiene mediante un número finito de operaciones de suma, resta,
multiplicación, división y com posición de funciones de las funciones: constante,
potencia (y - x a ), exponencial (y = a x), logarítm ica (y = lo g a x),
trigonométricas y trigonom étricas inversas), su derivada mantiene la m ism a
estructura, es decir, también se expresa com o una función elemental, mientras que
en la integral indefinida, esto solamente sucede en condiciones m uy especiales.
Por ejemplo, las integrales sim ples com o
l ^ i x . f e * d x .
J V i + x 3 dx , J ser¡(x2) d x , j c o s( x 2) dx
no pueden ser expresadas en términos de “com binaciones finitas” de funciones
elementales.
10www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-17-320.jpg)
![INTEGRAL INDEFINIDA
Del punto de vista práctico, la integración se presenta como una operación más
com plicada que la derivación, pues ésta tiene reglas generales de derivación;
mientras que para la integración es posible hacer artificios que son válidos para
clases particulares de funciones. Cada caso particular requiere un ensayo, una
tentativa, por lo que se recomienda práctica, más práctica y más práctica.
1.4.1 I N T E G R A C I Ó N P O R S U S T IT U C IÓ N O C A M B I O D E V A R I A B L E
Para hallar la integral indefinida por este método, dividim os nuestro análisis en
dos partes: reconocim iento del m odelo y cam bio de variable.
En el reconocim iento del m odelo realizamos la sustitución mentalmente, mientras
que en cam bio de variable escribim os los pasos de la sustitución.
El procedimiento de sustitución en la integración es comparable con la regla de la
cadena en la derivación. Recuerde que para funciones derivables y = f { u ) y
u = g (x ), la regla de la cadena establece
Si hacem os la sustitución u = g(x), entonces a partir de la definición de la
integral definida tenemos
A sí, hem os probado la siguiente proposición:
]
P ro p o sició n 3. Si y = f ( u ) es una función derivable de u, u = g ( x ) es una i
función derivable de x y F es una antiderivada de /, entonces |
J f ( g ( x))g'(x)dx = F(g(x)) + C (Reconocim iento del m odelo)
Si hacemos el cam bio de variable u = g(x), entonces du = g '( x )d x . Luego,
d
J f ' { g ( x ) ) g ' ( x ) d x = f { g ( x ) ) + C = f ( u ) + C
J f ( g ( x ) ) g ' ( x ) d x = J f ( u ) d u = F ( u ) + C
Ejem plo 16. Calcule J (x 3 + l ) 4 3x2 dx.
Solución
Sea t = x A + 1 . entonces d t = 3 x 2 dx . Luego,
IIwww.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-18-320.jpg)
![TOPICOS DE CÁLCULO - VOLUMEN II
í X 4
Ejemplo 17. Halle la integral I -dx.
J Vx5 + 1
Solución
Si t = x 5 + 1 , setiene d t = 5x 4d x . Entonces
f x 4 , 1 f 5x 4dx i r ,,, 1 7 £í„
T 'f •- dx = r Tr , = c f “ d t = - - - t 6/7 + C
J Vx5 + 1 5 J Vx5 + 1 5 J 5 6
= ¿ 7 ( * 5 + i ) 6 + c
r Sexdx
Ejem plo 18. Calcule la integral J - ^ = = = = .
Solución
Si u = e x , se tienedu = e * d x . Luego, se obtiene
f S exdx f du
...... = 5 --- = 5 arcsen u + C = 5 arcsenfe*) + C
J Vi - e2* J V l^ ü 2
f s e n h x c o s h x
Ejem plo 19. Calcule I = — ----------— - — dx.
J (1 + senh 2x ) 5
Solución
S i consideram os u = 1 + se n h 2x , se tiene d u = 2 senh x cosh x d x . Luego,
f ? du 1 í 1 u“4 1
/ - J - ¡ ^ - 2 j U d U ~ 2 ( ^ ) + C - - 8(1 + s e n V x y + C
f arcsenV x dx
Ejem plo 20. Halle I — ■ = = — .
■/ V x — X 2
Solución
r- . ' 1 d x d x
Si se hace u = a rc se n V x , se tiene du = ------- — = = — ■— ..... . Por tanto,
V T ^ x 2V x 2V x - x 2
r arcsenVx dx f 2
J — — = J 2u d u = u + C = [arcsenVx] + C
= arcsen2Vx + C
Observación 4. En ciertos casos, es necesario realizar algunas operaciones en el
integrando para que el cambio de variable sea másfácil de realizar.
12www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-19-320.jpg)
![INTEGRAL INDEFINIDA
Ejemplo 21. Calcule I
I 2 + J2 + J 2 + 2cos (5/x + 4) •x 1/2dx.
Solución
En el integrando, aplicam os la identidad trigonométrica
9 1 + eos 9
eos — = ------ —
2 2
Q
ó 1 + eos 0 = 2 e os2 —
- í
1 = 2 + 2 + |2 [ l + eos (5V3c + 4)] •x i/2dx
-i.
!2 + 12 + 2 cos 5-^ + 4 ■x~1/ 2dx = J 2 + 2 eos
5 V * 4- 4
1/2dx
5 V x + 4 5 _ . 16
Si u = ----- — -, entonces du = —~x ,¿dx <=> — du = x ' ‘ d x . Luego,
8 16 5
32 f 32 32 / 5 V x + 4
/ = — I eos u du = — sen u + C = — sen I ----- g— | + C
Ejem plo 22. Halle / = J
x dx
e3* ( l - x)4
Solución
Luego de expresar el denom inador en una sola potencia, tenemos
x e x dx C x e x dxf xe dx r xe
= J e 4x( l —x ) 4 = J (ex —.e 4x( l —x ) 4 J (ex - x e x)4
Lucho, hacemos u = e x —x e x . Entonces du = —x e xdx ■*=> —du = x e xdx
l)c esiii manera, se obtiene:
/
f du _ 1
J u4 3u 3
+ C =
3 e 3* (l - x ) 3
+ C
13
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-20-320.jpg)


![TONICOS Dii C Á LC U LO - V O LU M LN II
13. J cos(7x + 4 ) d x
14. J c l'2x~r,) dx
15. J (lnX+ l ) e xlnxdx
16.
dx
x ln2x
f dx
17. ---------
J x lnx
18. J 4 xe x dx
dx
19.
20./
sen2x V c o tx - 1
tan2x
sen x e
c o sJx
ev*3e
2'. I
‘I
dx
23.
(1 4- x 2) ln(x 4- Vi + x 2)
arctan* + x l n ( x 2 + 1 ) 4 - 1
1 -f X 2
1
R. - s e n ( 7 x 4- 4) 4- C
R. - e i2x- ^ 4- C
R. x x + C
R. —--------b C
In x
R. ln IIn x I 4- C
(4 e )x
R. ------ ~ + C
1 4- In 4
3
R. - - ( c o t x - 1 )2/3 4- C
R. - e ta,>2* 4- C
2 ( 3 eÆ )
R. t~ T ~ + cIn 3
R- 2 J l n ( x 4- -J1 4- x 2) 4- C
dx
R■ e arctanx 4- — ln(x2 4- 1) 4- arctan x 4- C
4
24,
25
26
J i
I
■ /
sen x
dx
■dx R. sen x 4- ■ •*+■ C
1 4- cos lO x
dx
R. — tan 5 x 4- C
V 2 x 4- 1 - yjx
R. 2 ( V 2x 4- 1 4- V x ) — 2 [a rc ta n V 2 x 4- 1 4- a rcta n V x ] 4- C
^ f ( X 2 - 2 x + l ) 1/5 j
27. -------- ---------------- dx
J 1 - x
R. - - ( x - 1 ) 2/5 4-C
16www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-23-320.jpg)
![28. J x 2x(nx + 1)dx
' V2 + x 2 —V2 —x 2
x 2x
R . — + C
INTEGRAL INDEFINIDA
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
f
/ V ^ T
h
V4 — x 4
dx
-dx
+ sen x
x - arctan 2x
+ 4 x 2
ln ( ln x )
■dx
f ln (ln x j
J x l n x
I
dx
2X 4- 3
dx
V e * - 1
x c o s x
/
f sen x
J
/
V2 - se n 4x
dx
4 + 5 c o s2x
dx
4 + 5 se n 2x
dx
-.dx
ex + 4
In 3x
x In 5 x
d x
ln (x + V x 2 + 1)
/
i
/
/ v r
43. j Vl + c o s x dx
«. J.
1 + x2
+ se n x d x
d x
*• arcsenf t ) - senl’" ' © + c
/?. - [(x + l ) 3/2 — (x - l ) 3/2] + C
R. tan x - s e c x + C
1 1
/?. - l n ( l + 4 x 2) - - a r c t a n 2(2 x ) + C
o Z
1
R. - l n 2( ln x ) + C
R. - x - ^ K 2^ 3) + c
R. 2 arctanVfc^ - 1 + C
R. - a r c s e n _
2 V2
+ C
1 (2 tan x
R. - a r c t a n ) — -— ) + C
R.
1
(L tan x
A 3 J
(2 cot x
V 3 )■
arctan ( — =— |+ C
1
R. - - l n ( l + 4e x) + C
R. In — ln|ln5x| + ln x + C
R. - [ln (x + V x 2 + 1)] + C
R. — 2 V l — sen x + C
e x + e x
R. 2 V l - c o s x + C
R. a rc ta n (e *) + C
17www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-24-320.jpg)
![y f W -
TOPICOS DE CÁLCULO - VOLUMEN II
d x 4f dx 4
45' ~ r = = /?• ~(Vx + 1) 3/2 - 4(Vx + 1)1/2 + C
J vvx + 1 á
4 8 . I j;Z sen l 'fsenx + x ros r In r id r ß , ì x 2 senx + ^
2 '
f arctanVx
• J v ï + æ + x * d x R • tarctan^ r+ C
*n í ( x - 2 ) , _ _ f y f x 2 - X + l
' j *• 2 arcse" (-----Ï----- ) + c
3. j x2senx~i(senx +xcosx Inx)dx
'■ í ~ i------ —------ R. J l n x + V l n x + ... + C
e lr,(2x)4 in x + V ln x + ... + o o — x
f eos 6x + 6 eos 4x + 15 eos 2x + 10
J eos 5x + 5 eos 3x + 10 c o s x dX R - 2 s e n x + C
f sen 8 x d x 1/'sen24x
5L I 9+ senHx R' J^arctan(— 3— j + C
f c o s2x (t a n 2x + 1) 1
52. —---------- ----------- —— dx R --------------------- 1- r
J (sen x + c o s x ) 2 1 + tan x
49.
f Ise c x - tan x
b3‘ J Jse c x + t a n x d* R' >n|secx + tanx| - ln(secx) + C
54. J c s c 3x d x R. - - [ e s c x c o tx 4- ln|csc x - cotx|J + C
55. J s e c 3x d x R. - [ln lse c x + tan x| + s e c x tan x] + C
f e 2x 2
5 6 ' J 4 t+~é*dX fi- - ( e í - l ) 3/2 - 2 (e I + l ) 1',2 i - C
r V ^ T e arctan * + ln f ( l + x 2)'íx2eX- x2] + V é ^ = T
57. I ---------------- *-------------dx
J l1 4- y ^-!p x 4- y2pX — v2 — 1
R. earctan* + ^ ln 2 ( l + x 2) + arctanx + C
4
q s f x d x n 1
J ( x - l ) 5e4x R■ ~ 4 (x —l ) 4e4Ar + C
18www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-25-320.jpg)
![2ex + e x
59- 1 3^ - ^ dx
In x dx
x 3( ln x — l ) 3
4 dx
60
61
/
/
f ---------- =
J cos x v l -
INTEGRAL INDEFINIDA
fi. l n |V 3 e 2* - 4 V 3 - e " 2*| + C
1
R. -
2 x 2( ln x - l ) 2
+ C
se n 2x + 2 c o s2x _____________________
R. 4 ln [(tan x — 1) + V ta n 2x - 2 tan x + 3] + C
62. J (4 — 3 l n x ) 4 d ( ln x )
f e * V e * + 2
J ex + 6
x 5 dx
63 •dx
■ /
■ J
x 3 - 8
. 1 + tan x
65. | -------- — d x
sen 2x
/?. - — ( 4 - 3 1 n x ) s + C
Ve* + 2
fi. 2 V e * + 2 - 4 a rc ta n ----- -------- h C
x3 8
fí. Y + - ln | x 3 - 8 | + C
/?. -ln | c sc 2 x - cot 2x + tan x + C
6 6 . U n a función /: R -
«o ) = - f y / ' W = l2 + 1
es continua en E y satisface:
x + |1 - x|
Halle f(x ).
x < 1
R. /W = arctan* - 2 '
(. ln ( x 2 + 1) - arctan x - In 2 , x > 1
67. H alle la ecuación de la curva para el cual y" = y que es tangente a la
x
2
recta 2 x + y = 5 en el punto (1; 3) R. y = —+ 1
68. Halle la ecuación de la curva cuya tangente en el punto (0; 2) es horizontal y
/ 10
tiene punto de inflexión en ( — 1; "g- ) y y " ; = 4.
2 vR. y = - x 3 + 2 x 2 + 2
x 2 + V i + x
69. E n cuentre la an tid eriva d a de / ( x ) = — j---— — , de m od o que dicha
antiderivada pase p o r P ^0;
VTTx
7 0 9
2 80/
, „ r3 , 6 3 6 _______
R. (1 + x ) / - (1 + x ) - - (1 + x ) + - + - V l T x
L8 5 L 1
+ 1
19www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-26-320.jpg)




![Ejem plo 33. Calcule / = J dx.
Solución
Separando la integral en la sum a de dos integrales, se tiene
I = J ~ d x + J e x n x d x
¡
Para la integral / , hacemos j u ~ ^ n x = > d u = —
vdi? = e x d x =$ v — e x
A sí,
1= j ~xdx+eX]nx~I ~^dx=e * l n * +c
r ^.garctan*
Ejem plo 34. Calcule / = í -----------------dx.
J (1 + x2)3/2 ux
Solución
g arctan x
Como la integral de — ^ 2 es inmediata, elegimos
garctan x
d v = - ..2 dx
1 + x 2
TÓPICOS DE CÁLCULO - VOLUMEN II
Luego, tenemos
x e ar<
V T + x 2 J ( 14*2)372
1 ~ ’'n- ■ --- ~ j — ---~dx
J
E n la integral J consideram os
1 , x dx
u = ■■■•. = * du = - -
V í T ? ( i + * 2) 3/2
g arctan x
dv = — ------—dx => v = e arctanjc
1 + x 2
Luego, se tiene
~ ”—^an x r
i =
V i + x 2 v r + i ^ j ( i + * 2) 3/2
dx
-i «arcían x ( v _ <
Portante, l = i - -■_ !? i i + c
2 V i + x 2
24
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-31-320.jpg)

![v3
TÓPICOS DE CÁLCULO - VOLUMEN II
E JE R C IC IO S
Calcule las siguientes integrales indefinidas.
1. J x 2 ln x dx
2. J (7 + x — 3 x z)e~x dx
3. J x se c2x dx
4. J a rc se n (2 x)dx
_ f ln x
* J ^
6 . J ln (x + V i + x 2) dx
7. j eos ( ln x ) dx
8 . J s e n ( ln x ) d x
9. J x a rcta n 2x dx
R. — (3 ln x — 1) + C
ñ. ( 3 x 2 + 5 x - 2 ) e _* + C
fí. a :ta n x + ln|eosx| + C
V i - 4 x 2
/?. x aresen 2x h------------------ 1- c
1 + 2 ln x
-— --------1- C
4 x 2
R. x ln (x + V 1 + x 2) - V 1 + x 2 + C
X
R. - [ s e n ( ln x ) + eos (ln x ) ] + i'
/?. - [ s e n ( ln x ) — eos (ln x ) ] + C
R- 2 [(*2 + l)a rc ta n 2x - 2x arctan x + ln ( x 2 + 1)] + C
10 / a rc se n 2x dx
ii.
fx,n(hr)
Lí,J i r r n c v — c o n v V
f —
J (x + i y
R. x aresen2* + 2VI - x 2 aresen x - 2x + C
R. lnx |ln(lnx) - 1| + C
x 2 + 1 ( X — 1
x 2 dx
( x c o s x - sen x ) 2
( x 2 + l ) e x
R.
R.
R.
-ln (— )
Vx + 1/
sen x ( e o s x - sen x )
2x e x
x + C
eot x + C
x + 1
e x + C
26www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-33-320.jpg)
![INTEGRAL INDEFINIDA
15.
16.
17.
18.
19.
2 0.
2 1 .
22.
23.
24.
25.
27.
2H.
x e*
(1 + x ) 2
dx R. ----------+ e x + C
1 + x
x e
_ 1 ^
x arctan yjx2 — l d x R. - x 2 a rc ta n V * 2 - 1 - 1 + C
(1 - x 2) 3/2
arctan *
d x
arcsen x 1
/?. +—ln
-dx R.
V i - x 2 2
arctan x
1 - x
+ C
1 + x
+ In|x| — l n i / l + x 2 + C
esc5x d x R.
X (X + 1
V i — X 2
e 2*c o s ( e * ) d x
e a*se n ¿ x d x
- c s c 3x c o tx - - ( e s e x c o tx + ln|cscx + cotx|)j + C
R. Vi - x 2 ln f------ + 2 arcse n x + C
Vx + 1 /
/?. e*sen(e*) + cos(e*) + C
■[a sen bx —b cos bx J + C
a rc ta n (V x + 1) d x
ln (V x + V i + x ) dx
se n 2( In x ) dx
a 2 + b 2
R. (x + 2 )a rc ta n V x + 1 - V x + 1 + C
R. {x + ln (V x + V x + 1) — ~ V x 2 + x + C
R. x se n 2(ln x ) - - [x se n (2 ln x ) - 2 x eos (2 In x )] + C
^gS en x C 0 S 4 X _ ^
C O SJX
d x
R. e sen x - - [see x tan x + ln |secx + tan x |] + C
( x 2 - se n 2x )
-dx R. x ( c s c x - c o t x ) + C
x - sen x eos x + x eos x - sen x
(arccos x - ln x) dx R. x árceos x - V 1 - x 2 — x ( In x - 1) + C
27www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-34-320.jpg)
![29. Si / (x ) = —a / ( x ) y g"(x) = b g(x), donde a y b son constantes, hallar
la integral:
TOPICOS DE CÁLCULO - VOLUMEN II
j f M g " ( x ) dx
’• /
30. I 4 x 3 arcsen —dx
x arctan x
31. I ~~7Z-----T^rdx
í
’-P
I
35. I
(1 + x 2) 4
x 4 — x arctan x
32. | — — -------— — dx
(1 + x2)2
, a rc se n V x
33. | ------ —— dx
V x
, 1/ x
■dx
.. r x 2se c 2x
37. I — -------------------^~z^dx
J (tan x - x sei
> /
^ 2cai.2,
(tan x - x se c 2x ) 2 '
1
dx
arcsen
39 1 ---------- *
x3
41. j arctan^jVx - 1 dx
43.
/ senh" ‘J r
-d x
(e 2* - x 2) ( x - 1)
45. J -------- d x
x 2ex
se n x + 1
(x + c o s x ) 2
a ln (x + a + V x 2 + 2 a x )
(x + a ) 2
a + b
lf(x)g'(x) - f'(x)g(x)} + C
-yx 2 - 1 + c
/
34. eos x ex dx
36.
38.
:eos x d xJ x e x i
J x arctan V x 2 - 1 d x
• /
’■ /
c o sh 2x d x
(x senh x - c o s h x ) 2
ln (2 + Vx)
42. | — ' ' ' dx
Vx
44.
I
(x sen x + eos x ) ( x 2 - c o s2x )
d x
f x c o s x
J (x -
■ /
f
• J - = = [ l n ( l + X )* - ln (l - x )*]
46. J cosh 3 x eos 2 x dx
í * 5 /l+*48. I :In ( --------Jd x
J VI - x 2 Vi - x /
d x
28www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-35-320.jpg)
![1.5.1 Integrales de algunas funciones que contienen un trinomio cuadrado
de la form a: /
dx f dx
I
INTEGRAL INDEFINIDA
1.5 TÉC N IC A S DE IN T E G R A C IÓ N
I. í — 5— --------- II. í —
J p x 2 + qx + r J j rp x 2 + qx + r J j p x 2 + qx + r
n ] [ (ax + b)dx f ( ax 4- b)dx
J p x 2 + qx + r J J p x 2 + qx +r
En los casos (I) y (II), es suficiente completar cuadrados en el trinom io y aplicar
las fórm ulas que correspondan: (23), (24), (25) ó (26).
En los casos (III) y (IV ) se usa el siguiente artificio:
a aq
ax + b = — (2 px + q) — — + b
2p 2p
La expresión 2px + q es la derivada del trinom io cuadrado. Entonces
(ax + b)dx a f (2px 4- q)dx ( a q f dxr (ax 4- b)dx a C (2px + q)dx / aq f
J p x 2 + qx + r 2p j px2 + qx + r V 2 p) ) ;p x 2 + qx + r
a / a q
= —— ln [p x ¿ + qx + r| + I b - — 1A
2 p V 2 p)
Por otro lado,
(ax + b)d x a f (2px + q)dx / aq f dxI' (ax + b)dx __ a f (2px + q)dx ^ ^ aq^ f
J yjpx2 + qx + r J J p x 2 + qx + r '2p/ J J p x 2 + qx + :
a /—^--------- ( acl
= - V p x 2 4- qx + r 4- b - — j B
p 2p)
I ,as integrales (¿4) y (B) son de los casos I y II, respectivamente.
Ejem plo 37. Calcule las siguientes integrales:
3 dx f dxf 3 dx f
J 4 x z 4- 4x - 3 J x 2 - 2x 4- 10
f 2 dx í 5 dx
J lx 2 4- 6x 4- 18 ^ i V — x 2 —8x — 12
Solución
Com pletando el cuadrado en cada trinom io y aplicando las fórm ulas de
m ig ra ción , tenemos
29www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-36-320.jpg)







![INTEGRAL INDEFINIDA
III. I N T E G R A L E S D E L A F O R M A :
J se n (mx) cos(nx) d x , J sen(mx)sen(nx)dx, J eos(mx) cos(nx) d x ,
J senh(mx) co sh (n x ) d x , J senh(mx)senh(nx)dx y
j co sh (m x) co sh (n x ) dx.
Para calcular estas integrales se usan las fórmulas:
1
a) sen (mx) eos (nx) = - [sen(m - n)x + sen (m + n)x]
b) se n (m x )se n (n x ) = - [cos(m - n ) x - eos(m + n) x]
c) eos (mx) eos (nx) = - [cos(m - n) x 4- eos (m + n) x]
1
d) se n h (m x) co sh (n x ) = - [senh(m + n)x + senh(m - n)x]
1
e) se n h (m x) se n h (n x ) = - [cosh(m + n)x —eosh(m — n)x]
1
f) co sh (m x) co sh (n x ) = — [cósh(m + n) x + eosh(m — n)x]
E jem plo 44. Calcule las siguientes integrales:
a) J sen 2x eos 3x dx b) j eos 3x eos 4x dx
c) j senh d) J cosh 4x senh x dx
Solución
a) J sen 2 x c o s 3 x dx = - J [sen(2 — 3 )x + se n (2 4- 3 )x ]d x
= 2 / ^S6n ~ S8n X^ X ~ 2 ( ------ 5-*" C°S * ) +
b) J c o s 3 x c o s 4 x d x = - J [ c o s ( —x ) 4-eos 7 x]d x = - ^ s e n x 4-- s e n 7 x )
c) J senh 3x senh 4 x d x = - J [ c o s h 7x — c o sh x jd x
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-44-320.jpg)
![d) J cosh 4 x se nh x d x = —j [senh 5 * - senh 3 x ] d x
1/1 1
= 2 5 C° S ~ 3 C0S 3x) + ^
E n este ejemplo, se han usado las identidades:
s e n h ( - u ) = - s e n h u , s e n ( - u ) = - s e n u
c o sh (— u ) = c o s h u , c o s ( - u ) = c o su
E je m p lo 45. Calcule las integrales:
y í i ~ . í sen4* + eos4*
a) I se n 3( 3 * ) t a n 3 * d * b) ------ ------------T-dx
J J sen2* — eos2*
f e o s * r
c) ■ ■dx d) I eos3* sen 3* dx
J V'sen7 (2 *)eos* J
So lu ción
f f sen43x
a) / = se n 3(3 * ) tan 3 * dx = ------— dx
J J eos 3 *
_ J (1 - cos23 * ) 2
TOPICOS DE CALCULO - VOLUMEN II
eos 3 *
-dx
b)
= J(sec3x - 2 eos 3* + cos33*)d*
1 2 1 f
= -ln |sec3 x + tan 3*| - - sen 3* + - I (1 - sen23*)(3 eos 3* dx)
1 2 1/ 1
= -ln |sec3 * + tan 3*| - - sen 3* + - (sen 3* - -s e n 33* + C
j 3 3 V 3 /
1 , 1 1
= -ln |sec3 * 4- tan 3*| - -se n 3* - - s e n 33* + C
■J J 7
f sen4* + eos4* r 4 (2 + 2 cos22*)
-----i -----------J~ d x = ------------- ñ--------d x
J sen2* - eos2* J - e o s 2*
-lí (se c 2* + eos 2x )d x
1 , 1
= --rh i(s e e 2 * + tan 2*| - -s e n 2* + C
4 4
38www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-45-320.jpg)
![c) /
INTEGRAL INDEFINIDA
cos * I f cos x dx
- f C0SX H - 1 f
J Ysen^(2xT co sx V 2 7 J V s e n 7x c o s8*
Se observa que esta integral no se adapta a ninguno de los tipos estudiados en
(I). Cuando se presentan estos casos, a veces, es conveniente transform ar a los
otros casos, es decir, a productos de tangentes y secantes ó cotangentes y
cosecantes. E n este ejemplo, transform ando a tangentes y secantes (dividiendo
entre e o s5*, numerador y denominador) se obtiene:
1 f se c4* 1 f 1 + tan2*
' = V l 2 8 J ta n 7/3* = Í V f J ta n 7/3* O 0" * d * )
1
, . .tan 7/3x + tan 1/3* ) s e c 2* d *
4V2J v J
= —rrz ( —- cot4/3* + - t a n 2/3* ) + C
4V2V 4 2 )
f 7 f (1 + eos 4*
d) } = I cosJ2* sen 3* dx = J ^-------------J eos 2* sen 3* dx
4 / ( c „ s 2 x Sen 3 ^ + Í J eos 4*(cos 2* sen 3x)dx
= - J [sen * + sen 5*]dx + - J [eos 4* sen *+ eos 4* sen 5x]dx
1 1 1 ir
= — —eos * - - eos 5* + - I [-sen 3* + sen 5* + sen * + sen 9x]dx
( 1 1/1 1 1
= - —eos * - - eos 5 * I + - - eos 3* —- eos 5 * - eos * -----eos * + C
4 V 5 / 8 3 5 9 /
3 1 3 1
= - - eos * + — eos 3*- — eos 5 * - — eos 9* + C
8 24 40 72
E je m plo 46. Calcule las siguientes integrales:
f f f sen^x
a) j tanh42 * d x b) I seeh3x d x e) I —— dx
, ^
d)
e o s“*
f s e n 43 * f
----- T¿—dx e) ta n ¿ x s e c * d *
J e o s33 * J
Solución
Se observa que ninguna de las integrales se adaptan a los casos estudiados, por lo
que será necesario efectuar algunas transformaciones. E n efecto, •
39
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-46-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
a) I tanh4 2 x dx = J (1 - sech2x )2dx = J ( 1 - 2 sechz2 x + sech4 2 x) dx
= x —tanh 2x + J (1 —tanh22 x) sech2x dx
1 / 1
= x - tanh 2x + -(ta n h 2x - -ta n h 3 2x) + C
1 1
= x - - t a n h 2x - - t a n h 32 x + C
¿ O
b) J sech3x dx = J - J l - tanh2* (sech2* dx)
(Si u = tanh x , du = sech2x dx)
= —[tanh x Vl - tanh2x + arcsen(tanh x)j + C
l r
= - [tanh x sech x + arcsen(tanh x)] + C
f sen2x f r
^ J cös^xdx = J tan2x Sec4* dx = I tan2x^1 + tan2x)(sec2x dx)
= I (tan2* + tan4x)(sec2x dx) = ^tan3x + ^tansx + C
J 3 5
(sen43x r (1 - cos23x)2 r
3 J cos33x “ J ^ 3 *dx = J(sec 3* ~ 2sec 3* + cos 3* )
= J Vl + tan23x sec23x dx - ^In|sec3x + tan 3x| + ^sen3x
A
1 r
= ~ |tan 3x sec 3x + In|sec 3x + tan 3x|] - A
1 1 1
= gtan 3x sec 3x - -In|sec 3x + tan 3x| + ^ sen 3x + c
e) I tan2* secx d x = J y/sec^x^l(tan x s e c x d x )
1 ,
= - | s e c x t a n x - ln|secx + tanx|] + C
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-47-320.jpg)
![INTEGRAL INDEFINIDA
dxf dx
l:)riii|)lo 47. Halle la integral J + usando la su stitu ció n x = 2 tan i
Sol ut-ion
( .uno x = 2 tan 0 , dx — 2 sc c 29 d9. Entonces
dx l f sec29 dB 1
i
f dx I f see 0 dB 1 f
1 f (1 + cos 2 9 )d 9 1
'i
)
- i J
1
( arctan - 4- , ,
16 V 2 4 + x 2
2 16
x 2 x
sen 20
+ C = — [0 + sen 0 cos 0] + C
16
4 -C
l’.tra regresar a la variable original x, en vista de que tan # = - , se construye
d triángulo
A partir de este triángulo, se obtiene que
sen 0 =
V x 2 + 4
y eos ti = —
V x 2 4- 4
E J E R C I C I O S
Calcule las siguientes integrales indefinidas:
1.
/
+ 2x — 8 dx
R.
9 dx
3.
V 9 x z - 12x + 13
3 dx
4 x 2 — 16x 4-17
4 — Ix
-[(x 4- l)Vx2- « x - 8 - 9 ln |x 4- 1 4- J x 2 4- 2x - 8|J 4- C
fl. 3 ln [3x - 2 4- V 6 * 2 - 1 2 x T l 3 ] 4- C
fi. -a rc t a n (2 x - 4) 4- C
V x 2 4- 2x —8
:dx
ß. - 7a/x2 4- 2x - 8 4- 11 ln x 4- 1 4- v x 2 4- 2x - 8| 4- C
41
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-48-320.jpg)






![TOPICOS DE CALCULO - VOLUMEN II
12 dx
/;
Ejemplo 53. Calcule / - , __________________
(2x - l ) / ( 4 x 2 - 4x - 8 )3
Solución
Com pletando el cuadrado en el trinom io y haciendo la sustit jción
2x - 1 = 3 sec 9, dx = - sec 9 tan 9 d.9
Resulta
/
= /
- /
■ /
12 dx
(2x - 1 ) V (4x2 —4x —8)3
12 dx
{2.x —l) [ ( 2 x — l ) 2 — 9 ]3/2
18 sec 8 tan 9 dd 2
3 s e c 0 2 7 t a n 30 9
J cot26 d9 = — j (esc29 —1)d 6
2 , 2 /
= — [—cot 6 — 0] + C = — (■
Ejem plo 54. Calcule J
Solución
Si se sustituye
/
9 V V 4 x 2 - 4x - 8
e _:>f dx
2x - 1
+ aresen— -— J + C
(9e~2x + 1)3/2'
3e * = tanfl, e = - - s e c 29 d9 , se tiene
= J
e x dx
[(3 e ~x) 2 + I ]3/2
r ~ 3 sec29 d9 r
J sec39 3 J eos 9 d9
--se n 9 + C
Vi + 9e~2*
+ C
48
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-55-320.jpg)



![f ( x 5 - x ) _ r (x * - l ) ( x dx) f [(z 2 - 3) 2 - ] z dz
J V ^ T 3 JV F T 3 " J z
f z **
= J ( z 4 - 6 z 2 + 8 ) d z = Y - 2 z 3 + 8z + C
TÓPICOS DE CÁLCULO - VOLUMEN II
b) Haciendo z 2 = x 2 + 3, z dz = x dx se obtiene
z
= - [ z 4 - 1 0 z 2 + 4 0 ] + C
Vx2 + 3 ,
= ----- ------( x 4 - 4 x 2 + 19) + C
c) Si se sustituye z 2 = x 2 + 9, z dz = x dx resulta
r x 3 dx _ r x 2(x dx) f ( z 2 - 9) ( z dz)
J (X2 + 9)3/2 - J ( x2 + 9)3/2 - J
dz
9 1 ,
= z H ------h C = - (z + 9) + C
z z
1
( x 2 + 1 8) + C
V x 2 + 9
d) Haciendo z — 3 — x 2, x dx = - - d x se obtiene
f x 5 dx í x 4(x dx) f (3 - z ) 2( - í dz)
J (3 - x 2)4 ~ J ( 3 - x 2)4 = J i?
1 f / 9 6 1
2 J +
1 / 3 3 1
“ 2 ^ ~ I * + z ) + C
x 4 - 3 x 2 + 3
~ 2 (3 - x 2) 3 + C
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-59-320.jpg)

![TÓPICOS DE CÁLCULO - VOLUMEN II
5 /
e x¡e2x - 4 - 2 e 2x( e x + 2)
15. | — ------------- — "■■■■■ ■■ —— —dx
2{ex + 2 ) 4 e 2x~ - 4
R. —nex + 2| - V e 2* - 4 + c
_ f 2 x 2 - 4 x 4- 4
16. j - — dx
J 4 3 + 2x —x 2
R. aresen - (x - 1 )V 3 + 2 x - x 2 + C
17
18.
dx
( x2 - 2 x + 5 ) 3/2
( x 2 + 3 x )d x
R.
x - 1
4 V x 2 - 2x + 5
í ( x2 + 3x
J (x - l W x 2 -(X - l ) V x 2 - 2x + 10
R . V * 2 - 2a: + 10 + 5 In |V*2 - 2x + 10 + x + l| + - ln
V x 2 - 2x + 1 0 - 3
x - 1
+ C
m Í 4 ^ L
J V 4 — x 2
(3 + x 2) 2 x 3
2 0 '
V4 - x2
/? .------ -----(8 + x2) + C
21
22
23
/
f V y 2 ~ 4
i y 4
‘ J
■/
R. - -
. 2
( *2 + l ) 2 , 7 , 4
-------------+ (x 2 + 1) + -f* €
d y
(x2 —l)Vx2 - 2
2x2 4- 1
( x 2 + 4 ) 2
dx
dx
161
r — ( y 2 - 4 ) 3/2
■ Í 2 y 3 + C
_ Vx2 - 2
k. arctan--------- + C
x
x 1 4 x
2 x 2 4- 4J
( 2x 2 4- l ) V x 2 + 1
f 3 x a r c s e n x
25. I — . dx
R- r r la r c t a n r ----— — - 14- C
fi. arctan * ) + C
W 1 4- r 2/
J V ( i - * 2) 5
J V i - x 2 v i - x /
aresen x 1 [ x
(1 — x 2)3/7
i r x
2 l ~
-4-in
■Vi 4- x 2
AT+ 1
V T
4- C
dx
R ] n f 1 + X ) ( 2 7 3 1 s , 89 /25 + 6x 2
*■ ln l T ^ I A 3 z ~ 5 - zJ + g ó arcsen* “ * 2 ( — e T ' j + c-
donde z = J l - x 2
54www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-61-320.jpg)


![INTEGRAL INDEFINIDA
dx
Solución
l n este caso n = 2 y k = 2. Entonces
r dx x 2 (2 ) - 3 f dx
] (x 2 + 4 )2 “ 2.22(2 - l)(x2 + 4 )2-1 + 2.22(2 - 1) J (x2 + 4)
x 1 1 x 1 / x 2x
“ 8 ( ^ 4 ) + 8 ' 2 arCt3n 2 + C = 16 l arCtan 2 + Í ^ T í) + C
l'lem plo 59. Usando la fórmula de reducción, calcule / = J + .
1.5.4.2 I N T E G R A C I Ó N D E F U N C I O N E S R A C I O N A L E S P O R
D E S C O M P O S I C I Ó N E N F R A C C I O N E S S I M P L E S
P (x )
Sim la función racional f ( x ) = — -r, donde P (x ) y Q{x) son polinom ios
Q(x)
i <«primos de grados m y n (m ,n e N), respectivamente.
Si m < n, se dice que la función racional es propia y cuando m > n, se dice que
rs una función racional impropia.
Por ejemplo, las funciones racionales
x 5 - 6x2 + 7
y a t o2 x 4 + 8 J " 2x&+ 3 x 3 + 2
mm propias, pues el grado del polinom io del num erador es menor que el giado del
polinom io del denominador; mientras que las funciones racionales
3 x 4 - 2x2 + 7 _ 5 x 3 - 3 x 2 + 1
F(X) ~ x2 + 2x + 3 y " 2 x 2 - 7 x 3 + 4
son impropias.
P(x)
Si / (x) = es Una función racional impropia, por el algoritm o de la división,
uxisicn polinom ios C(x) y /?(x) únicos tales que
l’t o r r ^
-------= C(x) +
Q(x) Q(x)
ilmule el grado de R(x) es m enor que el grado de Q(x). C(x) y R( x ) son,
ii'speclivamente, el cociente y el resto de la división de P( x ) entre Q(x) .
I tío significa que toda fracción im propia puede ser expresada com o la sum a de un
polinom io y de una fracción propia. A sí, la integral de una fracción im propia
IMifilc ser escrita com o
í p t o , f , ( R t o dx
57www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-64-320.jpg)




Para x = - 1 en (**), se obtiene: 1 = 3A = > A = 1/3.
Igualando coeficientes de x 2 en (* * ) , resulta: Q = A + 2 D = $ D = — 1/6.
Igualando coeficientes de x en (* * ) , se tiene: 0 = —A + D + E = > E = 1/2.
fuego,
líje in p lo 63. Calcule J ■
Solución
C om o x 3 - 1 = (x - l ) ( x 2 + * + 1), aplicam os el método del ejemplo anterior.
1)c este modo, la descom posición en fracciones sim ples es
1 A B (2 x + 1 ) + ^
x 3 - 1 ~ x - l + x 2 + x + 1
Elim inando denom inadores.se obtiene A = 1/3, B = -1 / 6 . C = -1 / 2 . P or tanto.
1 1 1 í 2x ~~
= -ln|x + 1| - gln(x2 - x + 1) + -^arctan + c
dx
dx
E je m p lo 64. Halle / - J <•* _ 2) 2^ - 4 x + 3 ) 'm plo 64. Halle / —
Solución
( orno (x - 2 ) 2( x 2 - 4 x + 3) = (x - 2 ) 2(x - 3 )(x - 1), entonces
(x —2 )2( x 2 — 4 x + 3) x — 2 (x - ¿V x - i x - 1
l lim inando denominadores, obtenemos la ecuación principal:
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-68-320.jpg)

![INTEGRAL INDEFINIDA
Determinando las constantes A, B, C y D por el procedimiento usado en los
ejemplos anteriores, se obtiene
1 . Í L Í _ j L _ - L 1
i9 J i u u2 u 3 + u - 169
1 >.69
69 r " k 69 + 1
1 1
du = -ln |u | H------t - r - r + ln|u - 1| + C
u 2u2
+ C
+ 1 2 (x 69 + l ) 5
K|em plo 67. Calcule 1 = J V tan x dx.
.Solución
SI lineemos t 2 = ta n x =» x = a rcta n t2 y d x =
21 dt
1 + t
entonces
f 2 t 2 dt _ f
1 ~ J i + t4 “ J ( T
2 t z dt
+ V 2 t + t z) ( l - V 2 t + t 2)
I ,ii l'actorización de 1 + t 4 se realizó del siguiente modo:
I f t4 = (t 2 + l ) 2 - 2t 2 = (t 2 + l ) 2 - ( V 2 t) 2 = ( t 2 + 1 - V 2t ) ( t 2 + 1 + V 2t)
I ,¡t descom posición del integrando es
A ( 2 t + V 2 ) + B t C(2t - s / 2 ) + D _ 212
t 2 + V 2 t + l t 2 - V 2t + l “ l + t4
Elim inando denominadores, se tiene
212 = [¿(2t + V2) + B][t2 - V2t + 1] + [C(2t - V2) + Z>][t2 + V2t + l]
Igualando los coeficientes de las potencias de t en los dos polinom ios, se obtiene
2A + 2 C ^ = 0 , (B + D ) + V 2 (C —A) = 2 ,
yj2(B - D) = 0 , V2G4 - C) + B + D = 0
Kesolviendo las ecuaciones, resulta
i4 = — V 2 / 4 , C = V 2/4 , B = — 1/2 , D = 1/2
I uego,
V 2
’ 4
r 2t + V2 _ i r _
J t 2 + V 2t + 1 f 2 J t2
dt V 2 f 2t - V 2 1 f
J t2 - V 2t + 1 t + 2 j t2 -t2 + V 2t + 1 4
hiiegrando y sim plificando, se obtiene
t 2 - V 2 t + 1
dt
V2t + 1
V 2 ,
/ = T ln4 t 2 + V 2 t + 1
donde t = Vtan x.
/^ ^2
— — arctan(V 2 t + l ) + — arctan (V 2 t — l ) + C
63www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-70-320.jpg)
![r
Ejemplo 68. Calcule I = í ------—
J 3 + 4
TOPICOS DE CÁLCULO - VOLUMEN II
sec2x dx
tan x + sec2x '
Solución
Escribim os la integral com o
l = [ x sec2* dx - f _____ x se ^ x dx _ f x sec2x dx
J 3 + 4 tan x + sec2x J 3 + 4 tan x + (1 + tan2* ) ~ J (tan x + 2) 2
Aplicando el método de integración por partes, elegim os
( u = x => du = dx
sec2x dx
dv = 71--------V = - -
(tan x + 2)2 tan x + 2
Luego,
dx
l = -----------_ +
r dx
J tan xtan x + 2 J tan x + 2
J
H aciendo t = tan x =* d t = sec2x dx en la integral ], se tiene
dxf sec2x dx r dt, f dx _ r _______ sec2x dx_______ r
J tan x + 2 J (tan x + 2)(1 + tan2x) J '(t + 2) ( 1 + t 2)
Descom poniendo el integrando en fracciones simples, tenemos
1 _ 5 . ~ l ñ ( 2t) + 5
■+ •
( í + 2) ( l + t2) t + 2 1 + t 2
Luego,
l r dt 1 r 2t dt 2 r dt
5 j t + 2 1 0 J 1 + t 2 + 5 J 1 + t 2
1 1 2
J = p ln|t + 2| — —— ln|l + t 21+ - a r c t a n t + C
b 10 5
1 1 2
7 = g In|tan x + 2| - — ln|l + tan2x| + -a rc ta n (ta n x) + C
Finalmente, obtenemos
(tan x + 2) 3* 1
/ — ------------- “ H----- ln
tan x + 2 10 sec2x
2
+ - * + C
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-71-320.jpg)
![INTEGRAL INDEFINIDA
E J E R C I C I O S
II,illc las siguie ntes integrales indefinidas:
4 x 2 + 6
/
í
I
/
/;
h
r -
x 3 + 3x
dx
-dx
( x 2 4- 4 ) 2
x 4 - 4 x 2 - 14a:
x 2 —2x — 8
dx
( x 2 + 2x + 5 ) 3
X ‘
^ ' 2 x 2 + 4
R. ln [x 2( x 2 + 3)] 4- C
8
4 ln [ x 2 4- 4| + C
-dx
R.
x ■> 68 , , 14 ,
R. — 4-x 4 -8 x 4 -— ln[x — 4 | — — ln|jí + 2| + C
2(x 4 1) 3 (x -t-l) 3 (x + 1
•4- , . „— ~ a rc ta n (— -— j 4- C
(x 2 4- 2x 4- 5)2 4 (x 2 4- 2x + 5) 8
X 2 4- X - 1
:3 - x 2 - x + 1
dx
x 4- 1
2 x 2 4- 3x
dx R.
R. ------------— + -ln | x - 1 | - - ln | x 4 - l| 4- C
2(x - 1) 4 4
ln|x| ln(x2 - 2x 4- 3) 2
•+ - arctan
3 <c t )
+ x
«)
10.
i
X 3 4- X 2
x 2 + x — 2
dx
1 I x 2 I
R. — 4 -ln ------ -
X x 4- 1
4- C
+ c
-dx
4 4- 5 x 2 4- 4
2 x 2 —3 x — 3
l ) ( x 2 - 2 x + 5)
1 ( x 2 + 1
R. - l n —z------
6 x 2 4- 4
arctan x 4- arctan - 4- C
dx
1
R. - l n ( x 2 — 2x 4 -5) - ln|x — 1 | -F -a rc ta n
( ^ )
4-C
r x 2
J 1 - x
■dx6
x 2 dx
x 6 - 10 x 3 4- 9
1
R. - l n
6
B. i l n
X 3 4- 1
4- C
+ C
4x 4- 1
X 2 4 -1
-dx
1 2x + 1
R. - ln (x 2 4- x + 1) — V 3 arctan
I I
2x
X 2 4- 1
-dx
V3 V3
2
4 /2 x
+ — arctan
V V 3 i )
+ C
/2 x 2 4- V
R. — arctan ----- —— 4- C
V3 V V3
65www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-72-320.jpg)

![IIN1cvjKAL LNUfcMINIUA
lU.
/
dx
X s + 1
V 5
R- ™ ln
20
2x2 - ( l - V5)x + 2
2x2 - (1 + V 5 )x + 2
V lO — 2 V 5 / 4 x - ( l + V 5 )
+ ------ — ------ arctan — +
1 0 V V 10 - 2V 5 /
V IO + 2V 5 ^ ( Ax - (1 - V 5 ) , „
--------— ------ arctan — |+ C
10 V V 10 + 2V 5
,'7.
2').
<0.
1!.
;»2.
u .
j V t a ñ h x d x
c o s x V s e n x + 1
1
Ä. - In
2
tanh X + 1
— — arctan(tanh x) + C
sen x + 2
dx
dx R. 2 V se n x + 1 — 2 a rc ta n V se n x + C
sen 5 x ( l + cos 5 x )
2 dx
1
R. - In
4
cos 5x - 1
•+ C
V c o s x sen x
5
/?. In
1 - V c o s x
1 + V c o s x
c o s 5 x + l 2 ( c o s 5 x + l )
+ 2 a rc ta n (V c o s x ) + C
C X 3
J i 1 3 !
/
/
d x fi. - [ x 3 - ln ( x 3 - 1)] + C
dx
x 3 + x - 1
( x 2 + 2 ) 2
4 x 2 - 8 x
( x - l ) 2( x 2 + l ) 2
Ä.
2 — x
I nJx2 + 2 ------ — arctan — + C
4(x2 + 2) ^ 4V 2 V 2
dx
R.
3 x - 1
(x - l ) ( x 2 + 1)
, ( * ~ 1 )
+ In — ■■ . 1 + arctan x + C
x 2 + 1 )
(■I
/
/
dx
( x 2 — x ) ( x 2 - x + l ) 2
x - 1
Æ. In
10
3 V 3
/2x - 1
arctan — —
V V 3
2 x — 1
3 ( x 2 — x + 1)
3 x + 2
x ( x + l ) 3
dx
4x + 3 x
R. — ------ —w + ln -
2 ( x + l ) 2 (x + l ) 2
+ C
+ C
67
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-74-320.jpg)

![Solución
I .ds cxponcntes fraccionarios de x - 1 son 1/2 y 1/3 .
Si se hace x ~ 1 = t 6 (6 = m. c. m. {2 ,3 }) => dx = 6 t sdt.
I liego,
f 6 t 5 d t r t 3 r , i .
J t 3 + t 2 ~ 6 ] T T i dt = 6 l ( t 2 ~ t + 1 - ^ ) dt
= 2 t 3 - 3 t 2 + 6 t - 61n|t + 1| + C
- 2¡x - 1 - 3 V x - 1 + ó V x - 1 - 6 1 n | V x — 1 + l l + C
INTEGRAL INDEFINIDA
Kjcinplo 70. Halle I = f dx
J V X - 1 + jx - 1 '
Eje m p lo 71. Calcule / = í í— — 1 —
J y] 1 + x 2 x
Solución
Se escribe
i ~ r 1 ■ —
/ = í I** ~ 1 ^ - 1f ;x2 “ 1 2* dx
J j l + x 2 x 2 J J i + x 2 ' ~ P ~
I luciendo el cambio de variable z = x 2, se obtiene
/ = - [ ,2 ~ 1 dz
2 J 1 + z z
I n ''sta últim a integral, el criterio estudiado nos sugiere reem plazar — = ^
I »namos al lector seguir este camino. Resolvem os la integral usando el siguiente
l = ± r _ j £ Z l ) d z _ _ l r ( z - l ) d z i r dz i r dz
2 J z v 1 + z V z — 1 2 j zVJ T T J 2 ) 4 ^ 1 2 J ¡ V P ^ T
1 , --------- , i
- ln | z + V z 2 - 1¡ -~ a rcse c| z| + C
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-76-320.jpg)


![TÓPICOS DE CÁLCULO - VOLUMEN II
Vx -;r -yx —■X
E je m p lo 76. Calcule / = J — — — dx.
So lu ción
1 1
Si se hace x = - = > d x = — ^dt. Luego,
t t2
* 11 _ J_
= - J - - ^ = - J V t 2 - 1 t d t , (u = t 2 - l , d u = 2 t d t )
E je m p lo 77. Calcule / = J ■
dx
(x + l ) 4 x 2 ‘
So lu ción
1 1
t * ~~ t
dt
Si se hace x + 1 = 7 = > dx = - - ^ d t . Luego,
t4 H
= - f y + t 2 + 3 í + 4 ln ( l - 1) + + c
1 1 3 1 x 1 x + l i „
-------- — H-------------- H-----------f- 4 ln -------r H--------- 1 + C
.3(x + l ) 3 (x + 1) 2 x + l ljc + l l x i
1 .6 .3 IN T E G R A L E S D E L A F O R M A J R [ x-. Jax2 + bx + c ) dx
E n este caso, R es una función racional en las variables x y V a x 2 + bx + c. U n a
integral de esta form a se calcula usando las ‘‘sustituciones de E u le r”. Estas
sustituciones permiten transformar el integrando en una función racional de
variable t. Se presentan 3 casos:
C A S O I. Si c > 0 , el cam bio de variable es V a x 2 + bx + c = tx + Ve.
Elevando al cuadrado, resulta
a x 2 + bx + c = t 2x 2 + 2V e tx + c
<=> (a - t 2) x 2 + (b —2 V c t ) x = 0
«=* x [ ( a - t 2) x + ¿ - 2 V c t] = 0
72www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-79-320.jpg)
![En esta última ecuación, elim inando la solución x = 0, se obtiene x = <p(t), que
es una función racional de t, y dx = (p'(t)dt. donde <p'{t) es también una
función racional de t. Por lo tanto,
J R(x,]y]ax2 + bx + c )d x = J R(<p(t); tcp(t) + Ve) <p'(f)dt
donde el integrando del segundo m iem bro es una función racional de variable t.
INTEGRAL INDEFINIDA
E je m p lo 78. Calcule ] = ■
J .
dx
x V 2x2 + x + 1 '
So lu ción
Haciendo y = V 2 x 2 + x + 1 = tx + 1 y elevando al cuadrado, se obtiene
2 x 2 + x = t 2x 2 + 2 tx
Elim inando la solución x = 0, se obtiene
2 t ■
dx
2 ( t 2 — t + 2)
dt, y =
t ( 2t - 1)
+ 1 =
t + 2
2 —t 2 ' (2 — t 2) 2 " 2 —t 2 1 ‘ 2 — t 2
Luego, reemplazando estos valores en la integral y sim plificando, nos queda
J' = f 2 d t
. . J 21 - 1
= ln|2t — 1| + C = ln
2 V 2 x 2 + x + 1 - 2
+ C
C A S O II. S i a > 0 , se hace la sustitución V a x 2 + bx -f c = V a x + t.
Elevando al cuadrado y sim plificando, se obtiene bx + c = 2V a íx + t 2. De esta
dx
ecuacion.se obtiene que x y ~ son funciones racionales de t y p or tanto, el
nuevo integrando es también una función racional de variable t.
E je m p lo 79. Calcule / = j
So lu ción
dx
x V x 2 + x + 1
Sea y = v x 2 + x + l = x + t.
Elevando al cuadrado, se obtiene x 2 + x + 1 = x 2 + 2tx + t 2. Lue«o,
1
1 - 2 1
, dx - 2
- t c + t •
d x , y =
- r + 1 - i
i - 2 1(1 - 2 t ) 2
Finalmente, reemplaitando estos valores en I y sim plificando, se tiene
V x 2 + x + 1 - x - 1
' J
dt
= ln
t — l i
t + 1
+ C = ln
V x 2+ x + 1 ~ X + 1
73www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-80-320.jpg)



![INTEGRAL INDEFINIDA
Entonces
/ = J x 1/2( z2x 3')1/2 ^ - - x 4z dz'j = - - | x 6z 2 dz —
2 r 1
_ 3 J ( z 2 - 1)2
z 2 c¿z
Para calcular la última integral, usam os la sustitución z = secB. A sí, se tiene
/ = -
2 f sec20 see 0 tan 0 dff
I /
2 f sec30 2 f
3 J tan3fl 3 jtan40
csc30 dd
1 4- cot20 ( - c s c 20 )d 0
= - [ c o t 0 c s c 0 4- ln|cote 4- cscfl|] 4- C
•+ ln
14- z
V P -
+ c
x V x 4 4 -x 1 i ,--------- ¡
-------------+ - ln x 3/2 + j l + x 3 4- C
J 6 1 l
V i + e 4x
E je m p lo 85. Calcule / = J
Solución
dt
Haciendo t = e x, dx —— resulta
t
-dx.
r V T T e 4* r v i + t4 r
' = J — ^ - d r = } - p - d “ l
V i + 14
r 2( l + 14) 1/4 dt
1 m 4-1
Com o m = — 2 , n = 4, p = — , ----------1- p = 0 E TL entonces
4 n
1 + t 4 = z 4t 4 ó t~4 4- 1 = z 4 y dt
Lueao, se tiene
- t 5z 3 dz
/= - j t 2(z 4t 4) 1/4t bz 3 dz = - J t 4z 4 dz = - J —-
- ' - 1 /
dz
1
- z - - l n
z 4 - 1
z — 1
1 z 2 + 1
4- -a rc ta n z 4- C
z 4-1
Finalmente, retornando a ia variable inicial x, se tiene
V i 4- e 4x 1
/ = ------------------------ln
e * 2
V i 4- e 4x - e >
V i 4- e 4x 4- e*
1 / V i 4- e 4ArN
4- - arctan I ------—----- | 4-
77www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-84-320.jpg)

![Calcule las siguientes integrales:
f ¿x
1. I — — 57= R. 2 V x — 3 x 1/l3 + 6x 1/6 — 6 l n ll + x 1/6 ! + C
J Vx + Vx 1 1
r -J~x Hy 1n
2 ‘ J y + x 4/5 2x1/2 ~ Y xV 1° + 10x1/10 - 10arctan(x1/10) + C
f 5 x 2 + 2 0 x - 24
3. -------- ;-------- ------ fl. 2(x + 5 ) s/2 - 20(x + S ) 3/2 + 2(x + 5 ) v " + C
J V x + 5
4. [ ............... ....... ... ................. R. - arctan (1 + - V 2x — 3^ + C
J (2x + 5 ) V 2 x - 3 + 8 x - 12 2 V 2 /
f 8 x + 2 l V 2 x - 5 (2 — x — 5 ) ( 8 V 2 x — 5 + 1 5)
5. -----------; ....... d x R. ------------------------------------------ - + C
J 4 + V 2 x - 5 6
r dx
6. I ------ — 777— ;----------------------------------------------------------------------------------- t t f t t
J (x + I ) 3/4 - (x + I ) 5/4 7 J
f (x — 2 ) 2/3 d x _____ / V x - 2
Z ] ( X - 2 ) V > + 3 *. + C
f x 1/7 + x 1/2
8. x 8/7 1S/14 dx /?. 7 X 1/7 - 1 4 X 1/14 + 2 8 In C x1/14 + 1) + C
f V x + i
9. I - = ---- 1
J V F + i
INTEGRAL INDEFINIDA
E JE R C IC IO S
■dx
4 4
R. — x 5/4 — - x 3/4 + 2 x 1/2 + 4 x 1/4 - 2 l n ( l + V x } - 4 arctan - + C
11
12.
x - 9 , 4 /3x - 1 2
d x R. - ln|x + 9| - ^ a r c t a n I - -------— ) + C
x + 9 ' 3 V2x + 18/
f 9 V T =rx ,----------
— ........d r R. a rc s e n x + V 1 - x 2 + C
J V T T x
í-j
f 2 3 ¡2 - x 3 / 2 + x z/3
J ( 2 - x ) 2 d X 4 (2^ ) + C
13. j sjsen2x + sen x dx /?. - Vsen x - sen2x - arcsenVl - sen x + C
14. J V cos2x + c o s x dx Ä. V c o s x -c o s 2x + arcse n V l-e o s x + C
79www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-86-320.jpg)






![TÓPICOS DE CÁLCULO - VOLUMEN II
Descomponiendo la última integral en fracciones simples, se obtiene
f [1 /2z + 4 1 í {2z - 2) + 12
1 ~ ] [ s U 2 + l J 5 z 2 — 2z + 5
dz
- 1 í f 2z 4 ___ —
5 J iz 2 + 1 + z 2 + 1 z 2 -
2z — 2 12
dz
2z + 5 (z —l) 2 + 4J
= ^ Jln(z2 + 1) + 4 arctan z - ln(z2 - 2z + 5) - 6 arctan ( ^ y ~ ) ] + c
+ C
i r ( z 2 + i
“ 5 r i z 2 - 2 z + 5
+ 4 arctan z - 6 arctan^
tan2ó + 1
ln + 2x - 6 arctan ^
/ tan 2 - 1
+ C
E J E R C I C I O S
Calcule las siguientes integrales:
dx
1.
2.
4.
5.
6.
7.
/
í
/
/
/ I
4 + 3 e o s *
dx
2 + sen x + 3eos*
dx
2 + sen *
dx
5 - 3 eos *
sen x dx
+ sen x
f sen2*
J 1 + eos2*
dx
tan:
R. - arctan — —
7 l V 7
V 6 ,
fí. — ln
6
t a n ^ - 1 + V ó
+ C
4* C
2 2 tanj + 1
R. — arctan --------— ------1 + C
V 3 V 3
■t / x „
R. -arctan ^2 tan-J + C
R. X
1 + tan 2
/tan *^
7 T
+ * + c
S
dx
sen24* + tan24*
/tan *
Æ. v 2 arctan ^ j - * + C
I r 1 /tan 4 x M „
». - g [ « ( 4 * ) + ^ arctan + C
86www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-93-320.jpg)



![Ix V l - x
24. I — ■ dx
4 T = x
■ í
i ' :
I
dx
V i + cosx
a rc se n V 2 x
26. | rfr
V 1 - 2 x
,'4* + l
27. | — d *
n
m + x
--------- dx
fl. - V 4 x 2 - 12x + 8 - l ( 2 x - 3 )V 4 x 2 - 12x + 8 -
O
7 . _______________
- - ln 2x — 3 4- V 4 x 2 - 1 2 x + 8 + C
O I I
/?. V 2 ln jse c ^ + tan^| + C
R. V 2 x - ( a r c s e n V 2 x ) ( V l - 2 x ) + C
R . x - 2 ln|2* + l| + C
/?. yjmx + x 2 + m ln (V x + 4 m + x ) + C
TÓPICOS DE CÁLCULO - VOLUMEN II
29.
30.
/
íi
V i — x 2
x “1
se n 2x d x
arcse n x d x
+ b c o s2x
, 2 a + x l a - x
31. 1 ---------- I-------- d x
/
■ /
x — x
V x + 1 - V x 2 + 1
d x
->3/2
(1 — x ) arcsen x 1 ln x
D _ _____ ____________________ , f*
' * 3 x 3 6 x 2 3
( a + b 1/2 fyfa t a n x x
r~z--------r u — x
R. V a 2 - x 2 - 2 a I---------- 1- C
y a + x
2 ^
/?. - (x + 1 )3/2 + - [ x V x 2 4- 1 + ln (x + V x 2 + 1)] + C
r ( x 2 - l ) d x 1
33‘ J (Su& u=x+-)x V l + 3 x 2 + x 4
/?. i c o s h - ^ ^ i l ^ + t a n h - 1
3 + V 5 ^ ^arcse c ( 2 x 2 + 3 )
“ 1 )
+ C
34. J V i
d x
V a 3 — x 3 .
2
3
/?. x arcse n ( |+ C
a 3/2
35.
/
4 —x
2 + x
dx i?. 3 arccos ( ~ y —) + 3V x2 - 2x + 8 4- C
90www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-97-320.jpg)


![INTEGRAL INDEFINIDA
(cosx - sen x)
6 0 . ¡(x+s^rdx
1
2
u ‘~‘ w
J T + ~9
/■
i
5 + sen 2x
dx
+ C , u = x + V * 2 + 1
1 / se n x + c o s x
B ' ¿ " " “ I------2,-----)
+ C
dx
( x 2 eos2a + x sen 2a + 1)2
x cos a + sen a
eos3a Vx2 cos2a + x sen 2a + 1
:“i- C
63. f sech5x dx
J
1 3
R. —sech3x tanh x + - [sech x tanh x + arcsen(tanh x)] + C
64. / (tan x + secx)20 sec2x dx
6 5 . /
■ í ,
J cos4xV4 - cot2x
V(1 + x 2)5
66
dx
V(x - l ) 3(x + 2)5
(eos 2x —3) dx
4 ix - 1
R • ö ------
3 ^ x 4- 2
ñ . ---- tan x(2 + tan2x ) V 4 — cot2x + C
3
67
J: -dx
,------- v ( i + *2)5 J ( i + x2y v i + x2
R. ln (x + V I + x ) 2 - _ , — - V „„ -------------------- + C
5 x 5 3 x 3
68
j- v'sen3(2x)
dx
4 V 2 r-
j se n bx
Sugerencia: hacer u = c o tx
' V i + X 8
<>9. I ---------- dx
>r ,13
R . ----- — V c o t 5x + C
(1 + x 8) 3/2
r . - , „ -i- c
f 3i sen2x
7<)-J
7L í “J C O SJ
dx
cos3x v sen 2x
12x12
R. — Vtan5x(5 tan2x + 11) + C
V 2 1 ,_____
R. (tan2x + 5)Vtan x ■+■C
93www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-100-320.jpg)


![TOPICOS DE CALCULO - VOLUMEN II
3. ^ [/ (i) ± g ( i )] = ^ / (i) ± ^ 5 ( 1) (Propiedad Distributiva)
¿~m i=m i-m
n
4. a) ^ [ / ( i ) - / ( ¿ - 1)] = f ( n) - f ( m - 1) (Propiedad Telescópica)
:=m
n
b) 2][/(0 - /(£ - 1)] = - /(O)
n
5- a) ^ [/(i + 1) - f ( i - 1)] = f ( n + 1) + / (n ) - f ( m ) - f ( m - 1)
i~m
(Propiedad Telescópica)
n
b) £ [ f ( i + 1) - /( i - 1)] = f i n + 1) + /(n ) - f { 1) - /(O)
400
E je m p lo 1. Calcule el valor de ^ ( V ¿ — V i — 1 + 4).
¡=5
Solución
Por la propiedad 3, se tiene
400 400 400
^ ( V 7 - V i — 1 + 4) = ^ ( v '7 - Vt - l ) -r y 4
; = £ ; = 5 i = S
E n la primera sumatoria, aplicando la propiedad 4-a para / ( i) = V i , m = 5 y
n = 400, se obtiene
400
^ ( V 7 - V i - 1) = (V4Ó 0 - v 4 ) = 18
1= 5
En la segunda sumatoria, aplicando la propiedad 1-a para k = 4, m = 5 y
n = 400, se tiene
^ 4 = (4 0 0 — 5 + 1)4 = 1584
Por tanto,
400
]T(V7 - Vi - 1 + 4) = ^ ( V i - Vi - l ) + ^ 4 = 18 + 1584 = 1602
96
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-103-320.jpg)
![INTEGRAL DEFINIDA
Ejemplo 2. Calcule una fórmula para ^ [ ( ¿ + l ) 2 - (i - l ) 2].
Solución
- ;2Si / ( i) = i 2 , entonces /(/ + 1) = (t + l ) 2 y f ( i - l ) 2 = (¿ _ i ) 2. p or tant0)
por la propiedad telescópica 4-b, se tiene:
n
^ [ ( ¿ + l ) 2 - (¿ - l ) 2] = (n + l ) 2 + n 2 - l 2 - O2 = 2n2 + 2n ó
1=1
n
^[(¿ + l)2- ( i - l ) 2]) = 2n(n + l) (a)
í—1.
C'omo (¿ + l ) 2 - (i - l ) 2 = 4¿, reemplazando esta igualdad en (a ) se obtiene
n
^ 4i = 2n(n + 1)
1=1
De esta parte se deduce una fórm ula m uy conocida:
V 1. n (n + 1)
L 1~ 2
í = i
E jem plo 3. U sando las propiedades de la sumatoria, demuestre que:
, V - n(n + l) , v V , n(n + l)(2n + 1)
1=1 1=1
c) ^ ¿3 = n2(n + 1)2 d) ^ ,4 _ n (n + 1 )(6 n 3 + 9 n 2 + n - 1)
30
i=i 1=1
Solución
a) V e r ejemplo 2.
b) Consideram os / ( i) = ¿3. Usando la propiedad 5-b, se tiene
n
^ [ ( t + l ) 3 - (i - l ) 3] = (n + l ) 3 + n 3 - l 3 - O3
í = i
Sim plificando en am bos lados y luego aplicando las propiedades 3-b, 2-b y 1-b
de la sumatoria, obtenemos
n n n
^ T ( 6 i2 + 2 ) = 2 n 3 + 3 n 2 + 3 n <=> 6 t2 + 2 = 2 n 3 + 3 n 2 + 3n
Í=1 1=1 1=1
n n
<=> 6 ^ í 2 + 2 n = 2 n 3 + 3 n 2 + 3n 6 i 2 = 2 n 3 + 3 n 2 + n
i= i ¿=i
97www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-104-320.jpg)
![Finalmente,
n (n + 1 )(2 n 4-1)
TÓPICOS DE CÁLCULO - VOLUMEN II
I 6
í =i
c) y d) Ejercicios. Sug. para c): considere / ( i) = ¿4 y use la prop. 4.
Z
a (a n — 1)
a 1 = -------------- .
a — 1
£=1
Solución
Aplicando la propiedad 4-b a / ( i) = a' y luego aplicando la propiedad 2, se tiene
n n ■ n
^ ( a ‘ - a '- 1 ) = a " - 1 <=> ^ T ( a ' - — ) = a " - 1 <=> ^ ( - --------)a‘ = an - 1
i = i 1=1 i = i
Finalmente,
V i _ a ( an ~ 1)
Z a ( a - 1 )
n
E je m p lo 5. Determ ine una fórm ula para ^ sen kx.
k = l
So lu ción
Para calcular la sumatoria de senos o cosenos, se considera como / ( i) la
cofunción de la función que aparece en la sumatoria y se aplica la propiedad
telescópica 5-b. En este caso, f ( k ) = eos kx. Así, se tiene
n
^ [c o s (k + 1) x —eos(k —1) x] = cos(n + 1) x + eos nx —eos x — 1
k =i
Utilizando las identidades trigonométricas para c o s(a ± b) y sim plificando, se
sigue
n
^ ( - 2 sen x sen kx) = co s(n + l ) x + c o sn x — c o sx — 1
k =i
n
- 2 sen x ^ sen kx —eos(n + 1) x + eos n x — eos x —1
k = 1
Finalmente,
z
cos(n + l ) x + cosnx —e o s * — 1
sen kx = ---------------------------------------------------
2sen x
98www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-105-320.jpg)
![INTEGRAL DEFINIDA
n
Ejemplo 6. Halle una fórmula para ^ fc fe!
fc=i
Solución
Si f ( k ) = (k + 1)!, p o r la propiedad 4-a, se tiene
n
^[(fc+ l)!-/c!] = (n + 1)1-1
k = 1
n
J][fc!(fc + l)-fc!] =(n + l ) ! - l
k=l
Finalmente,
^fcfcl = (n + l ) ! - l
, „ r, v-> ta n h l9 / c x
E je m p lo 7. Determ ine una form ula para > --------------- .
Z_i sech 19 kx
k=1
Solución
Z
tanh 19 kx v~>
— — = > se nh 19 kx
sech 19 kx í-u
k= 1 k=l
Se procede de manera sim ilar a lo realizado en el ejemplo 5 para la función
trigonométrica. Si /(/c) = cosh 19 kx , por la propiedad 5-a, se tiene
H
^ [cosh 1 9 ( k + l ) x - cosh 1 9 (fc - l) x ] = cosh 1 9 (n + l ) x + cosh 19 n x - cosh 19 x - 1
k-1
n
2 senh 1 9 x ^ senh 19 kx = cosh 19(n + l ) x 4- cosh 19 nx — cosh Í9x - 1
k=l
finalmente,
n
V 1 cosh 1 9 (n + í ) x + co sh 19 nx - cosh 19 x - 1
> senh 19 kx = ------------------------------------------------------------------------
Z-j 2 senh 19 x
k=1
99www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-106-320.jpg)
![TÓPICOS DE CALCULO - VOLUMEN II
n
E je m p lo 8. Halle una fórm ula para /? = ^ bk se n(x + ky).
k = 1
Solución
A plicando la propiedad 4-a a f ( k ) = bk se n(x + ky), se tiene
n
s e n (x 4- ky) - ¿ k_1 s e n (x + (k - l ) y ) ] = b n s e n ( x + n y ) - s e n *
k = l a
n ^ n
^ b k se n (x + k y ) — bk se n(x + ky —y ) = a
fc=l_________________ k= l
P
1 n
P —— ^¡T &fc[se n (* + /cy) eos y — sen y eos (x + /cy)] = a
fc=i
n
/c o s y se n y v-» ,
( l
-
- — J p -— - — ^ bk cos(x + ky) = a (1)
k =l ___________________ (
5
Para determinar (5), aplicamos el criterio inicial.
n
cos(x + ky) - ¿?/£_1cos (x + (k —1)y)] = bn co s(x + n y ) — e o s *
k = l
^ n
S —— ^ ¿ fc[cos(x + ky) eos y + se n(x + ky)sen y] = bn cos(x + n y ) - c o sx
k= 1
Luego,
sen y b -
S = ------------ ( « ) + - ; ------------- [í>n eos (x + n y ) — co sx ] (2)
o - e o s y o - e o s y
Finalmente, reemplazando (2) en (1) y efectuando las operaciones correspondientes,
obtenemos
b ( b - c o s y )
b2 —2¿cosy + 1
sen y(bn cos(x + ny) - eos x)
sen(x + ny) —sen x ----------
b —eos y
100www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-107-320.jpg)
![INTEGRAL DEFINIDA
E je m p lo 9. Determ ine una fórm ula para ^ ln(fe + 1).
k=1
Solución
Desarrollando la sumatoria y aplicando las propiedades del logaritmo, se obtiene
n
^ ln(fc + 1) = ln 2 + ln 3 + ... + In n + ln (n + 1)
k=l
= ln [2.3.....n. (n + 1)]
= ln [(n + 1)!]
E J E R C I C I O S
Determine una fórm ula para cada una de las siguientes sumatorias.
n
1
: = 1
. ^ ( V 2 i + 1 - -y/2i - 1) R. y/2n + 1 - 1
Í = 1
100
I ln(¡d h ) R- - ' " ( 5151>
k=i
3- I
n
4 4n
R.
(4fe - 3)(4fe + 1) ' 4n + 1
k- 1
4
Sugerencia: descom poner en fracciones parciales a:
4
■I
(4fc - 3)(4fe + 1)
2k + 3k 3 1 1
6k ' 2 2 .3 n 2"
k= l
2k + fe(fe + 1) 1 1
R. 1
Z
2 +
2 ^ " (fe2 + fe) ' 2 n + 2 2 n_1
/í= 1
e fc + 2 e 3n - e'1
k ~ 1
101www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-108-320.jpg)
![7.
8.
9.
10
11
12
13
14.
15.
16.
17.
TOPICOS DE C Á LC U LO - V O LU M E N II
n
Y —
k= 2
^ V/c + i - Vfc
fl. 3
2?i + 1
?i(n 4- 1)
fc=i
il
1¡i=1
n
I
V F T T
v ’n r 1 - 1
y 'n + 1
(/c + l)(/ c 2 + 5/c 4- 6 )
R.
n 2 + 3 n + 3
2 (n + 2 ) ( n + 3 )
( k 4- x ) ( k + x + 1 ) ( k + x + 2)
Z i lnkk[n(k + l ) ^ 1]
k = 1
I
fe=i
2k + 1
k 2(k + l ) 2
U
^ c o s ( 3 k x )
/¿=i
A V IO '' 100'=/
fe= l
100
+ 6k -f 4
^ s e n 2/c( 2 x )
k ~l
100
f í .
n ( 2 x + n + 3)
2 ( n + a: 4- l ) ( n 4- x 4- 2 ) ( x 4- 2 ) ( x 4- 1)
/?.
1
R.
2 ln 2 ( n 4- 1) ln ( n 4- 1)
n ( n + 2)
R. ------------ -
(n + l ) z
se n 3 (n + l ) x 4- se n 3 n x — se n 3 x
2 se n 3 x
2 6 9 / 1 0 2n - 1
R.
9 9 9 V 1 0 2n
R.
4 (n 4- 2)
/?. t a n 2 ( 2 x ) (1 - s e n 2002 x )
/?.
1
fc=i
1
16 1 6 (5 " ) 598
102www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-109-320.jpg)
![ì. ^ k x k 18 . > k x K~' fi.
n x n+1 - (n + l ) x n + 1
IN T EG R A L D E F IN ID A
ix
fc=l
II
19. ^ 5 k s e n (5 k - x)
k=l
5[(5 —cos 5)(5n sen(5n —x) + sen x) + sen 5(5n cos(5n —x) —cosx]
R.
4(13 —5 cos 5)
I ; " "
n r
16 csc kx
20
2 1 .
cot5/ex see9kx
k = 1
4[sen(2n + l)x + sen(2ruc) —sen 2x]
R. 6n + -------------------------— — ------------------------+
sen(2x)
[sen 4(n + l)x + sen(4nx) —sen 4x]
sen 4x
1e h - [3 sen a cos a]k
3k
k=l
Z :
e [ ( 3 ) ~ l] sen 2 a [(se n a cos a ) n - 1]
e - 3 se n (2 a ) - 2
!- Z
" 1 0 1 1 5
2 4 + lQk - 2 5 k 2 ^ 5 n + 4 + 5 n - 1 4
k=l
23.
k=i
^ k 2k fi. (n - l ) 2 n+1 + 2
k = i
n
24. ^ c o s 2k3;c fi. cot23 x [ l - c o s 2n (3 x )]
k=l
k=l
25- Z l o g „ r 2 2k) lo g „ r 2 2k+2ì ( l o g ^ v G 2 ( n + l ì )
V 1.-,-------- nfc V 3 + x [(3 + x ) n/2 - l]
26. > [ V à T x ] fi. - 1 J
k=l
V 3 + X - 1
103www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-110-320.jpg)
![2.2.1 PARTICIÓN DE UN INTERVALO CERRADO
Definición 1. Sea [a;b] un intervalo cerrado. Una partición del intervalo [a; b]
es el conjunto P de puntos Xo,x1(x2, - . x n; con a = x0 < x v < x2 ... < xn = b.
Se denota con P - {x0,xv x2, ..., x„}.
Observación 1
i) Toda partición P de [a; b] divide en n subintervalos al intervalo [a; b],
ii) La longitud de cada subintervalo [x¡„1;xt, para i = 1,2, ...,n , se denota
con Atx = x, — . Se verifica
n
y A¿x - b - a
(.=1
iii) Se llama norma o diámetro de la partición P al número
||P|| = máx{AiX / i = 1,2, ...,n}
iv) Cuando el intervalo [a; b] se divide en n partes iguales, la longitud de cada
subintervalo es
TOPICOS DE CALCULO - VOLUMEN II
2.2 CÁ LCULO D EL ÁREA DE UNA REGIÓN PLANA P O R SUM ATORIAS
Ax =
b —a
n
En este caso, los extremos de cada subintervalo son
x Q = a , xx - a + A x , x 2 = a + 2 A x ,..., x¡ = a + ¿ A x ,..., x n = b
2.2.2 A P R O X I M A C I Ó N D E L Á R E A D E U N A R E G I Ó N P O R Á R E A S D E
R E C T Á N G U L O S
Sea /: [a; b] -> R una función continua y no
negativa ( / ( x ) > 0) en [a;b]. Sea R la
región plana limitada por las gráficas de
y = / ( * ) > las rectas x — a , x — b y el eje
x (llam ada región bajo la gráfica de / de a
hasta b) (fig. 2 .1).
Sea P = { x 0, x 1, x 2, ...,xn} una partición [a; b].
Por la continuidad de / en [a;b], podem os
elegir un conjunto de puntos u t , u 2, —,u n, de
tal manera que / ( u ¿) sea el valor m ínim o de /
en [ x i- ij x j , i = 1 ,2 ,..., n. F'9' 2-1
104
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-111-320.jpg)
![Asi, construim os n rectángulos cuyas bases son los subintervalos de P y cuyas
respectivas alturas son / ( u 1) , / ( u 2), ...,f (u n). La s áreas de estos rectángulos son
/ ( iíJ A j X , / ( u 2) A2x , . . . , f ( u n)Anx respectivamente.
I.os n rectángulos considerados forman el llamado polígono rectangular inscrito
en R (fig. 2.2). E l área de este polígono lo denotamos con /(P ) , es decir,
71
K p ) = ' Y Jf(M i)Aix
¡=i
INTEGRAL DEFINIDA
De manera similar, elegim os v x, v 2, ..., vn en los n subintervalos de P, de modo
que / '(v ¿) es el valor m áxim o de f en [x ^ ^ x i], i = 1 , 2 , ..., ?i, y construim os los
n rectángulos cuyas bases son los subintervalos de P y cuyas alturas respectivas
son f ( v 1) , f ( v 2) ,. .. , f ( v n).
Kl polígono rectangular form ado por estos n rectángulos está circunscrito a la
región R (fig. 2.3) y su área, denotada por C (P ), está dada por-
n
C(P) = 2 J f ( v ¡)Aix
¡=i
Dadas dos particiones / y P2. Si / ( P J es el área del polígono inscrito y C (P 2)
es el área del polígono circunscrito, se verifica
l(P ) < C (P 2) para toda partición P1 y P 2 de [a; b] (I)
Sea L el conjunto de todas !as áreas de los polígonos rectangulares inscritos en R,
es decir,
i = {/ (P ) / P e s partición de [a; b]}
y U el conjunto de todas la áreas de los polígonos rectangulares circunscritos a R,
esto es,
U = ( C ( P ) / P e s partición de [a; b]}
105www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-112-320.jpg)
![TOPICOS DE CALCULO - VOLUMEN U
C om o cada número del conjunto L es menor o igual que cualquier núm ero del
conjunto U (por I), entonces L es acotado superiormente y U es acotado
inferiormente. Por lo tanto, existen
= su p (L ) y As = in f (U)
Por definición de ínfim o y de supremo, se verifica
/ (P ) < A¡ < As < C(P), de donde A¡ < As
Por lo tanto, el áreai4 de la región R (fig. 2.1), si existe, debe estar entre At y As,
es decir, A¿ < A < As
Se demuestra m ás adelante que A¡ = A¡. Luego, se puede definir el área A de la
región R com o
Tam bién se demuestra que si t1( t2, —, tn son puntos elegidos en los n
subintervalos, es decir, t¿ E [xi_1;x¡], i = 1, ...,n; entonces
Observación 2
i) Considerando la parte (iv) de la observación 1, si cada t¿ es el extremo
derecho de cada subintervalo (t¡ = a + ihx, i = 1,2,...n ) y teniendo en
cuenta que ||P|| -> 0 <=> n -* oo, entonces (II) puede ser escrito como:
(Estafórmula es un caso particular).
ii) Si cada t¿ es elextremo izquierdo de cada subintervalo. entonces
t¿ = a + (i - l)A x , i = 1,..., n
Eje m plo 10. Por rectángulos inscritos, calcule el área de la región Rlimitada por
las gráficas de y = x + 1, * = 0 , x = 3 y el eje x.
L a gráfica de la región se muestra en la Fig. 2.4. En este caso, f ( x ) = x + 1,
a = 0 y b = 3. C om o / es creciente en [0; 3], / presenta m ínim o en el extremo
izquierdo de cada subintervalo, es decir,
A — A¿ —As
(10
(III)
b —a
donde Ax = , = a + ¡Ax , i = 1, ...,n
n
Solución
3 - 0 3
t¿ = a + (t — l)A x , i = 1.... n , donde A x = ---------= —
n n
106
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-113-320.jpg)
![3 3 3 3 3
Kntonces t¡ = 0 + (/ - 1) - = - i -----y f ( t i) = ti + l = - i + l -------- .
n n n n n
l’or tanto, utilizando la fórm ula dada en la observación 2 y la sum atoria de i,
leñemos
INTEGRAL DEFINIDA
A = lim
n-»co
= lim -
*->oo /n
Fig. 2.5
Ejem plo 11. Por rectángulos circunscritos, calcule el área de la región R limitada
por las gráficas de y = x 2 , x = 3 y el eje x.
So lu ción
l;.l gráfico de la región R se muestra en la fig. 2.5. A partir del gráfico, se deduce
que a = O , b = 3 y, por tanto, Ax = 3/n.
C om o / es creciente en [0; 3], / tiene valor m áxim o en el extremo derecho de
cada intervalo. A sí,
t¡ = a + iAx ó ti = - i y f ( ti ) = — i2
Luego,
A = limI-YVn-*co n Z - i n¿
i=i
n-*co u J n-*co j l '
27 n(n + l)(2n + l)
3 £
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-114-320.jpg)
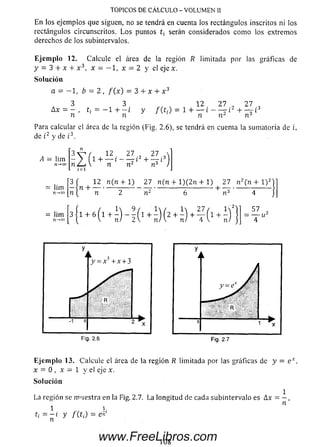
![IN T E G R A L D E F IN ID A
I n este caso, usaremos el resultado obtenido en el ejemplo 4 para a = Así,
1 e l/ n [(g l/ n y l _ j y
A = lim
lim
n-»cn
— / en
n L-a
= lim
n —»co
1 en(e — 1)
n e 1/11 — 1
,1¡n _ ]_
1
= (e - l) lim
,1/n
n
(*) Se hace el cam bio de variable x = — => lim
- e l/n
= (e - 1) u 2 (*)
x e
= lim — — - = 1.
n n->oo e 1/n —1 x->o ex —1
(A l aplicar la Regla de L ’Hópital al últim o límite)
Eje m plo 14. Calcule el área de la región bajo la gráfica de f { x ) = s e n * en
10; 7T/2J.
Solución
La gráfica de la región se muestra
en la Fig. 2.8. Así, tenemos
n
= s e n ^ ¿.
lim
n-*-»oo
TT V “ * TI
— > se n — i
2n jLu 2n
í=i
= lim
n-*oo
71
2n
i 1 + c o s £ ) - cos ( n S - cos (n + i
2sen®
( * * )
= lim
1+ cos(ín ) “ cos(§) ~ cos
sen
(s )
( s )
[1 + 1 - 0 - 0]
■ W ) .
1u2
( * * ) Se usa el resultado del ejemplo 5 para x = n¡2n.
109www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-116-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
E je m plo 15. Calcule el área de la región bajo la curva y = senh x en [0 ; 1],
Solución
La región R se muestra en la fig. 2.9.
Se tiene
1 1 (
Ax = - , t ¿ = - ¿ y / (tí) = senh - ¿
n n n J
í É senhG i)
1= 1
i c o sh (n + 1 ) —+ cosh ( n ■—^ — cosh i
1 v Jn nJ n
A = lim
n-> co 7
y - senhx
/
Fig. 2.9
lim
n->cc
- lim
n-*co
2 Se „ h ( i)
cosh ( l + i ) + cosh 1 — cosh ^ — 1 2 c o sh (l) - 2
(c o sh (l) - l ) u 2
Eje m plo 16. Calcule el área de la región limitada por las gráficas de y = 2¡x ,
eje x, y x = 9.
Solución
Para evitar la sumatoria de la raíz cuadrada, tom am os com o variable
independiente a la variable y, es decir, / ( y ) = y 2/4. La región está limitada por
las curvas / ( y ) = y 2/4, .9 (y ) = 9, las rectas y = 0 c y = 6 (fig. 2.10).
•El área del i-ésím o rectángulo es [g(Zi) - / (z ,)]A y .
Por tanto, el área de la región está dada por
110www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-117-320.jpg)

![E n esta sección y en las siguientes, hasta la sección 2.10, las funciones
consideradas están definidas en un intervalo / = [a; b], con a < b.
Definición 2. S i Px y P2 son dos particiones de /, se dice que P2 es un
refinamiento de Px cuando c P 2, Se comprueba fácilmente que si P2 es un
refinamiento de Pj , entonces ||P2|| < H H .
Definición 3. Sea una función acotada en / = [a; b] y
P = {x0,x 1, ...,xn } una partición de /. C on I¡ denotamos al j-ésim o subintervalo
de /, es decir, l¡ = xj_x)Xj, j = 1,
C om o / es acotada en ¡ , existen m¡ y Mj tales que
m¡ = in f{/ (x ) / x e Ij} ; M¡ = s u p {/ (x ) / x G !¡}
Se cumple: m¡ < / ( x ) < M¡, V x £ I¡, j = 1,2, ...,n.
Definim os:
a) La su m a in fe rio r de / para P, que se designa con S (/ ; P ), se define com o
n n
S(f; P ) = ^ m j(xj - xH1) = £ m ;Ayx
7=1 7=1
b) L a strma su p e rio r de / para P, que se denota con 5 (/ ; P ), se define com o
n
S ( / ; P ) = ^ M , A , x
j'=l
Eje m p lo 17. Sea / ( x ) = k la función constante definida en / = [a; b}. L a
gráfica de la función se muestra en la fig. 2.11. Se tiene
n n
S_(f. P) = ^ kAjX = k ^ áj-x = k(b - a), donde k = inf{/(x) / xe //}
■ • 7= 1
n n
S (f ,P ) - ^ fcA/X = k y A ,x = k ( i - a ) , d on d e /c = s u p { / ( x ) / x E /,}
TÓPICOS DE CALCULO - VOLUMEN 11
2.3 SUM A SU PE R IO R Y SUM A IN FER IO R
Fig. 2.11
112
Fig. 2.12
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-119-320.jpg)
![(
Ejem plo 18. Si f ( x ) = x , x e 1 = [a;b], entonces
n
£ ( / . p ) - * j - i A jx, donde xh x = in f{/ (x ) / i e l¡],j = 1 ,2 , , n
j = i
n
= ^ ]xjA jX , donde = su p {/ (x ) / x E 1¡},¡ = 1,2
j~1
I ;i gráfica de la función se muestra en la Fig. 2.12.
I.jcm plo 19. Considerem os "la función de Dirichlet”
c , s ( 1 , si x es racional , r ,
lo , si x es irracional 1 x e ~ ]
l’ara cualquier partición P se verifica que m¡ = 0 y M¡ = 1, j = 1,2, ...,n.
Luego,
n n
O.A;x = 0 y 5 (/ ,P ) = l. A ;x = ¿ - a
¡=i j=i
2.3.1 S I G N I F I C A D O G E O M É T R I C O D E L A S S U M A S S U P E R I O R E S E
I N F E R I O R E S
Las sum as superior e inferior poseen una interpretación geométrica simple.
Ln primer lugar, analicem os el significado del producto hjAjX, donde h¡ es nij
ó Mj y Aj'x es la longitud del subintervalo Ij = [ x j ^ x j ] .
Si hj > 0 . entonces hjAjX es numéricamente igual al área del rectángulo de base
/, y altura h¡. Si h¡ = 0 , entonces hjAjX = 0; y si hj < 0 , entonces hjA¡x es
numéricamente igual al opuesto del área del rectángulo de base ¡¡ y altura - h¡.
Por esta razón, al núm ero hjAjX lo denom inarem os área a lge b raica del
rectángulo cuya base es Ij y altura es hj , es decir, el área algebraica es positiva
si el rectángulo esta sobre el eje x y negativa, si está debajo de eje x.
lin la sección 2.2.2 (figuras 2.2 y 2.3), vim os que cuando / es no negativa en /,
S_(f>P) y S (f .P ) (que denotam os por I{P) y C ( P ) ) son, respectivamente, las
áreas de los polígonos rectangulares inscrito y circunscrito a R, donde R es la
región lim itada por las gráficas de /, las rectas x = a , x = b y del eje x.
INTEGRAL DEFINIDA
S(f,P) = Y
113www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-120-320.jpg)
![E n las figuras 2.13 y 2.14 se muestran, respectivamente, S ( f , P ) y S ( f ,P ) $ m a
una función que no necesariamente es positiva.
TÓPICOS DE CÁLCULO - VOLUMEN II
La condición de que / esté acotada en / = [a; b] es esencial para que existan los
valores m¡ y M¡ . Estos números se definieron com o los ínfim os y suprem os, en
vez de m ínim os y m áxim os (com o se hizo en la sección 2 .2 .2), ya que en esta
oportunidad no se exigió qug / sea continua.
2.3.2 P R O P I E D A D E S D E L A S S U M A S S U P E R I O R E S E I N F E R I O R E S
C om o / es acotada sobre /, existen m y M tales que
m = in f { / 0 ) / x E I } y M = s u p { / 0 ) / x E /}
P ro p o sició n 1. Sea / una función acotada i'n / = [a;b] y P = [x0,x-i. ...,x n }
una partición de /. Entonces
m (b - a) < S ( f , P ) < S ( f , P ) < M(b - a ) ( 1)
D em o stració n
Se tiene m < m, < Mj < M. M ultiplicando todos ios términos por A¡x > U y
sum ando las relaciones obtenidas para j = 1,2,..., n , obtenemos
n n n n
^ mAjX < nijAjX < ^ MjAjX < MA¡x ó
7= i 7= i ;= i j= i
« n
m X A¡x - ajx
j=i j=i
n
Com o ^ Ayx = b - a, entonces m (b - u) < 5(/, P ) < 5(/, P) < M(b - a).
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-121-320.jpg)
![INTEGRAL DEFINIDA
P rop osició n 2. Si / es una función acotada en /, y Px y P2 son dos particiones
de I tales que P2 es un refinamiento de Pr , (Pt c P2), entonces
‘0 •!(/. Pi) < S(f, P2) y S(f, Px) > S(f, P2)
b) Si P2 —/ tienen r puntos, entonces
í ( f , P 2 ) - S ( f , P í ) < r ( M - m ) P 1
S(f.P1)-Sif,P2)<r^M-m)Pi
D em ostración (se deja com o ejercicio para el lector).
Prop osició n 3. Sea / una función acotada en /, y Px y P2 dos particiones
arbitrarias de /. Entonces
• S ( / . P 1) < 5 ( / . P 2) ( 2 )
D em ostración
Sea P — P1 U P2. C om o Pt c P y P2 c f , por la proposición anterior, se tiene
S t f . P j l Z S i f . P ) y S ( f , P ) < S ( f , P 2)
Por la proposición 1, se tiene SJJ.P) < S(f , P) . Luego.
S ( M ) < S ( f , P 2)
2.4 I N T E G R A L E S I N F E R I O R E S Y S U P E R I O R E S
Denotem os con D al conjunto de todas las particiones posibles de l. Si f es
acotada en /, la desigualdad (1) es verdadera para todo P e D y asegura que el
conjunto {S( f , P) /■ P 6 D) es acotado superiormente v- el conjunto
S ( f , P) / P e o ) es acotado inferiormente.
D efinición 4. S i / es una función acotada en /, el número su p {£ (/, P ) / P 6 D}
se denom ina integral inferior de / en / y se indica com o
]_= f f ( x ) d x = sup (S(f, P ) / P e D]
Ja
El número in f(S(f,P) / P e D) se denom ina integral superior de f en / y se
indica como
1 1 5www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-122-320.jpg)
![2.4.1 P R O P I E D A D E S D E L A S I N T E G R A L E S S U P E R I O R E S E
I N F E R I O R E S
TOPICOS DE CALCULO - VOLUMEN II
Si / es función acotada en /. entonces
_ r b r b
]_ < J ó I f { x ) d x < I f { x ) d x
Ja Ja
(3 )
2. Si / es función acotada en /, entonces
m { b - a) < ) _ < ] < M(b - a) (4 )
donde m = in f { f ( x ) / x E 1} y M = su p { f ( x ) / x E /}.
3. Si / es acotada en /, existen q y c2 E I talesque
¿ = f ( c - j ( b - a) y / = / (c 2) ( ¿ - a ) (5 )
de m odo que m < / ( q ) < f ( c 2) < M.
4-. S i / es acotada en / y cE ( a ; b ) , se tiene
'•O pC rO
f ( x ) d x = j f ( x ) d x + I f { x ) d x
b r C r b
f ( x ) d x = J f ( x ) d x + J f ( x ) d x
2.5 I N T E G R A L D E R I E M A N N
D e fin ición 5. Se dice que una función acotada f : ¡ - > K es integrable R ie m a n n
en / si
r b
íJa
J = [ f(x)dx = í f ( x ) dx = f f ( x) dx
*'a Ja Ja
Por sim plicidad, se llama integral de / sobre / o integral definida de / sob re /
o integral de / de a hasta b.
En j f ( x ) d x , el sím bolo j es llam ado sím bolo de in tegración.
Este sím bolo, que es una S alargada, fue introducido por Leibniz para representar
la suma, que proviene de la palabra latina “sum m a”. Adem ás, f ( x ) es el
integrando, f { x ) d x es el elemento de integración, el número a es el límite
inferior y b es el límite superior. L a variable x no tiene significado especial, ya
que
í f f á d x = í f(z )d z = í f ( t ) d t = í f ( y ) d y - í f{u)du
Ja Ja Ja Ja Ja
etc.
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-123-320.jpg)
![l'.jcinplo 20. Sea f ( x ) = k la función constante. Por el ejemplo 16, pars
/ = [a; b] se tiene S(f, P) = S(J, P = k (b —a).
Entonces J = ] = k(b —a). P or lo tanto, / es integrable en [a; b] y se tiene
r b
k d x — k (b - a )
INTEGRAL DEFINIDA
JJa
Ejem plo 21 (función no integrable). Considerem os la función de Dirichlet
/': [0; 1] -» IR, definida por
x es irracional
x es racional
Para cualquier partición P de 1 = [0; 1] (ejemplo 19), se tiene:
S ( / ; P ) = 0 y 5 ( / ; P ) = l
Entonces 7 = 0 y J = 1 y, por tanto, / no es integrable en ¡.
Observación 3. Interpretacióngeométrica de la integral definida de una función
continua f en [a; b].
De la interpretación geométrica de las sumas superiores e inferiores (secc. 2.3.1),
deducimos que si R es la región plana limitada por las gráficas de f, las rectas
X = a , x = b y el eje X, y /4(fl) representa numéricamente al área de la región
R; entonces
a) Si f ( x ) > 0, V x 6 [a; b ] , A(R) = f f(x )d x
*a
b) Si f ( x ) < 0 , V x e [a; b] ► - A(R) = f f ( x ) d x
JQ
c) Si al número I f ( x ) d x lo llamamos área algebraica, para una función
Ja
arbitraria f continua en [a; b], esta integral definida de f en [a; b] representa
la suma de las áreas algebraicas de las regiones determinadas por la gráfica de f
y el eje X, desde x = a hasta x = b.
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-124-320.jpg)
![TOPICOS DE C A L C U L O - V O LU M E N II
E je m plo 22. L a gráfica de / consta de
segmentos de recta y una semicircunferencia,
com o se indica en la figura adjunta. Halle:
a) í / ( x ) d x b) í f ( x ) d x
J o J -6
c) f / ( x ) d x d) f |/(x)|dx
•'-6 J-6
e) E l área de la región limitada por la gráfica
de /, el eje x y las rectas x = —6 y x = 8 .
Solución
a) C om o el área del círculo de radio r = .4 es Ax = n r 2 = Ió ít u 2, entonces
A= —4ti
i
4
k
i
i
i
y *
/■ i
/ * i
/ ! !
“6 V y 5 ¿ x
-4
í A,
J / W ^ = - T = -
b) Dado que el área de un triángulo de base b = 2 y altura h = v es /12 = 4 u 2
/4
y el área del sem icírculo es A = — = 8n u 2, entonces
í f ( x ) dx = í / (x )d x + í f ( x ) d x = Az - A = 4 - 8tt.
J - 6 J - 6 J —4
c) Puesto que la integral definida desde —6 hasta 8 está form ada por la sum a de
/ A2
áreas algebraicas de un triángulo (A2 = 4 ), de un sem icírculo — = — 8n j,
de un triángulo (Á3 — 2) y de un rectágulo (A 4 = 12), entonces
r 8 r —4 /•4 r 5 /*8
I / ( x )d x = I / (x )d x + I f ( x ) d x + I / (x )d x + I / (x )d x
J - 6 J - 6 J - 4 J 4 J s
= 4 + ( — 87t) + 2 + 12 — 18 ■ 87T
d) C om o |/(x)| = — / (x ), V x G [ - 4 ; 4 ] , entonces
í / (x )d x = f / ( x ) d x - í f (x ) d x + í f ( x ) d x + í f ( x ) dx
j - ó J -6 ■'-4 **4 Js
= 4 - C— 8 tt) + 2 + 12 = 18 + 8 tt
e) El área de la región pedida es
4 ( R ) = í |/(x)| dx = [ f ( x ) d p T h ( ( - / ( x ) ) d x + [ / ( x ) d x + í f (x ) d x
J -6 J - 6 • '- 4 -M ->5
'= 4 — ( —87r) + 2 + 1 2 ( 1 8 + 87r) u 2
118www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-125-320.jpg)
![INTEGRAL DEFINIDA
Teorema 1 (C riterio de integrabilidad de Riemann). Si / es una función
;icotada en /, una condición necesaria y suficiente para que / sea integrable en / es
que dado e > 0 arbitrario, exista una partición P de 1 tal que
S ( f , P ) - S ( f , P ) < £ (6)
Demostración
;i) ( = * ) Por hipótesis, / es integrable en /. Si ¿ = su p [S{f,P) / P e D }, dado
£ > 0, existe una partición P1 de / tal que
J _ - ¿ < S ( f . P i ) ó ¿ - K f . P J < | (7)
Por otro lado, siendo ] = inf{ S(f, P) / P e D) y tomando el m ism o e > 0 ,
existe una partición P2 tal que
S(f,P2) < 7 + | ó S(f,P2) ~ ] < E- (8)
Sum ando m iem bro a m iem bro las desigualdades (7) y (8) y considerando que
/ = ], obtenemos
S(jr,P2) - S ( f , P 1) < E
Considerando Pí U P2 = P (es un refinamiento de P, y P2), tenemos
S(f, P ) - S(f, P) < S(f. P2) - S(f, P J < £
b) (< = ) Supongam os que dado £ > 0, existe una partición P de I tal que (7) es
verdadero. C om o
J_ > S ( f , P ) y ] < S ( f , P )
se obtiene 0 < J — J < 5(/, P ) - S(/, P ) < e. C om o £ es arbitrario, se obtiene
7 - 7 = 0 o 7 = 7
Por tanto, / es integrable en /.
Hasta ahora, I f ( x ) dx se ha definido solo si a < b . Por conveniencia, se dan
¿as siguientes definiciones:
Definición 6. Si a < b , se define
I f ( x ) dx = — ¡ f ( x ) d x , siem pre que I f {x ) d x exista.
h Ja Ja
Definición 7. Si / es una función definida en o. se define
I
,-a
f ( x ) d x = 0
a
119www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-126-320.jpg)
![TOPICOS DE CALCULO - VOLUMEN II
P rop osició n 4. Si f es una función continua en / = [a; b], entonces / es
integrable en /.
La demostración se deja com o ejercicio al iector.
2.5.1 P R O P IE D A D E S D E L A I N T E G R A L D E F I N I D A
1. Si / es una función integrable en /, entonces es integrable en cualquier
subintervalo [c; d] c /.
2. Si f es una función integrable en /, entonces para toda constante real k , k f es
integrable en / y se tiene:
f k f { x ) d x = k í f ( x) dx (9 )
Ja Ja
3. Si / y g son funciones integrables en I, entonces / ± g es integrable en / y se
tiene:
r b p b rb
l f ( x ) ± g ( x ) ] d x = f (x ) d x ± I g(x)dx ( 10)
Ja Ja Ja
4. Si f es integrable en los intervalos [a; c] y [c; b], entonces / es integrable en
I = [a; b] y se tiene:
f f ( x ) dx = í f ( x ) d x + í f ( x) dx (11)
Ja Ja Je
(Propiedad aditiva respecto al intervalo de integración).
Esta propiedad es válida para tres números arbitrarios a, b ,c siempre que las
tres integrales existan.
5. Si / es integrable en I = [a; b] y f ( x ) > 0 , V x E I. entonces
f f ( x ) d x > 0 ( 12)
Ja
6 . Si / y g son funciones integrables en /y f ( x ) < g(x), V x E /, entonces
í f ( x ) d x < í g(x)dx (13)
Ja Ja
7. Si / es integrable en / = [a; b] ym< f ( x ) < M, V x E /, entonces
m(b - a) < í f ( x ) dx < M{b- a ) (14)
-'a
8. Si / es integrable en I, entonces
f /(x)dx| S í f(x)dx (15)
Ja I Ja
120www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-127-320.jpg)
![1N I hC jKA L D t r lN IU A
2.5.2 T EO R EM A D EL V A LO R IN TERM ED IO PARA IN TEG R A LES
Teorem a 2. Si / es una función continua en I = [a; 6], entonces existe un
número c G / tal que
í f ( x ) dx = f ( c ) ( b - a )
Ja
Demostración
El Teorem a del V a lo r Intermedio de una función continua indica: “Si f es
continua en [a; b] y se cum ple que / ( a ) / '( ¿ ) , entonces para cualquier o)
entre / ( a ) y f ( b ) existe un número c entre a y b tal que / (c ) = 6)".
Por hipótesis, / es integrable en /, pues / es continua en I (Prop. 4). Luego, por
(14), se tiene:
m(b — a) < f f ( x ) dx < M(b - a)
Ja
donde m y M son el m ínim o y el m áxim o absolutos de / en I, respectivamente
(estos valores existen porque / es continua).
Luego, m = f ( x m) y M = f ( x M ) , con xm y x M G /, y
f bf ( x ) d x
f(Xm) ~ b - a ~ / (* m)
Por el teorema del valor intermedio para funciones continuas, existe c entre xm y
xM (c G /) tal que
fb f ( x ) dx r b
f (c) = — ------------, es decir, I f { x ) d x = / ( c ) ( ¿ — a ) , con c e I
b - a Ja
2.6 T EO R EM A S FUN D AM EN TA LES D EL C Á LC U LO IN TEG R A L
Teorema 3 (Prim er Teorem a Fundamental del Cálculo Integral o Teorem a de
Barrow )
S i f es una fu n c ió n c o n tin u a en / = [a;b ] y F es la fu n c ió n d e fin id a por
F(x) = I f { t ) d t , x G /, entonces se tiene
F '( x ) = ¿ ( / f ( t ) d t j = f ( x ) , v x e i
Demostración
Por definición, para x G [a; b] {x fijo), se tiene
, ,. F(x + h ) - F ( x ) f * +h f ( t ) d t - f i f ( t ) d t
F (x ) = lim -------------------------- lim ----------------- r-----------------
h-*o hh-*oh
, ! * f w t + c k f w t - s * f w t r v ( í ) d í
= h m ---------------------------- :-----------------------------= u m -------------------
h-*o h h-o n
121www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-128-320.jpg)
![Por el teorema del valor intermedio para integrales, para el par de números x y
x + h e [a; b] existe c entre x y x + h tal que
r X + h .
I f ( t ) d t = / (c )(x + h - x ) = hf(c)
Jx
Luego,
F'(x) = lim , c entre x y x + h
h->o h }
F '( x ) = lim f(c) , c entre x y x + h
h-0
F'(x) = / (x), V x E / , e s decir, F es una antiderivada de / en /.
Observación 4. Este teorema establece un enlace entre los conceptos de integral
definida e indefinida. Se prueba que una función f continua en I admite una
antiderivada dada por F(x) = / * f ( t ) d t , pues F '( x ) = f ( x ) , V x € /.
es un teorema de existencia, pues si f es una función continua en l, existe
F(x) = / * f ( t ) d t tal que F'(x) = f(x) , V x G7. Como F(a) = 0 , F es la
antiderivada de f en l cuya gráfica pasa por el punto (a; 0).
TÓPICOS DE CÁLCULO - VOLUMEN II
Teorem a 4 (Segundo Teorema Fundamental del Cálculo Integral)
Si / es una función continua en / = [a; b] y F es una antiderivada de f en /
( F '( x ) = f ( x ) , V x E /), entonces
[ f ( x ) d x = F ( b ) - F ( a ) = [F(x)]b (1 6 )
Ja a
Demostración
C om o F es una antiderivada de / en / y, por el primer teorema fundamental,
F definida por F (x ) = / f ( t ) d t es también una antiderivada de / en /, entonces
existe una constante c tal que F(x) = F(x) + c , V x E l.
Así, tenemos
F(b) = F(b) + c = f f ( t ) d t + c y F(a) = F(a) + c =
*a
C om o /Qa / ( t ) d t = 0, entonces
F(b) - F ( a ) = f f ( t ) d t
Ja
C om o la variable t no tiene significado especial, se concluye
í f ( x ) d x = F(b) - F ( a )
■'a
1
f ( t ) d t 4- c
122www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-129-320.jpg)
![INTEGRAL DEFINIDA
Observación 5
n) F (x)]ba es una notación para F(b) —F(a).
h) La fórmula dada en (16) es llamada “Fórmula de Newton-Leibniz” debido a
que estos dos matemáticos establecieron, independientemente uno del otro, la
relación íntima entre los conceptos de la derivada y de la integral. -El nombre
que se le da a esta fórmula es convencional, ya que ni Newton (1642-1727) ni
Leibniz (1646-1716) dieron exactamente con esta fórmula.
c) Obsérvese que la diferencia F(b) - F(a) no depende de la elección de la
antiderivada F, puesto que todas las antiderivadas se diferencian en una
constante, la que desaparece al efectuar ¡a diferencia. Por eso, al calcular una
integral definida no es necesario considerar la constante en la antiderivada.
a) Siendo / ( t ) = 1/(1 + t 2) una función continua, por el prim er teorema
fundamental, se tiene F'(x) = 1/(1 + x 2) , V x > 0 (es necesario notar que
F'{x) = 1/(1 + x 2) es válido para todo x e R). C om o F'(x) > 0 , V x R ,
entonces F es una función estrictamente creciente en R .
b) F"(x) = —2 x / { l + x 2) 2 (F presenta punto de inflexión en x = 0).
c) F '( 1) = 1/ 2 .
Finalmente, dado que F'(x) = 1/(1 + x 2) , entonces F (x) = arctan x + C para
alguna constante C. C om o F ( 0 ) = 0, entonces
0 = arctan(O ) + C => C = 0, es decir, F(x) = arctan x
Ejem plo 24. Calcule el valor de cada una de las integrales
So lu ción
a) U n a antiderivada de f ( x ) = 1/(1 + x2) en l = [ - 1 ; 1] es F ( * ) = arctan x
(en esta antiderivada, por la obs. 5-c, no se considera la constante). Luego,
E je m p lo 23. Sea la función F { x ) = ------- - d t . Calcule
Jn 1 + t0
a) F '0 0 b) F"(x) c) F’( 1)
Solución
f dx 1 ■■■ 7T y 7T n
J T + x 2 = [arctan x ] _ 1 = a rcta n (l) - a r c t a n ( - l) = - - - J = -
r 1t/2 jj.
b)J sen x dx = - [ c o s x ] ^ 2 = - ^ c o s - - cosOj = 1o
123www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-130-320.jpg)
![= C
o
TOPICOS DE CÁLCULO - VOLUMEN II
c) f e* dx = = e 1 — e° = e —1
Ja
f 1 1
d) I senh x d x = [coshx] = c o sh (l) - 1
Jq u
Com pare las respuestas obtenidas en (b), (c) y (d) con las obtenidas en los
ejemplos (13), (14) y (15) de este capítulo.
Eje m p lo 25
i) Sea G ( x ) = / “ f ( t ) d t , donde /: / = [a; b] ->R es continua y u = w (x ) es
una función derivable (u: —» /). Pruebe que
d
G'(x) = / ( u ) . u ', donde u' = — (u (x ))
ax
ii) Sea H(x) = f^ f ( t ) d t , d o n d e / y u = tt(x) tienen las condiciones dadas en
(i). Dem uestre que
d
H'(x) = - / ( u ) . u ', donde u ' = — (u (x ))
dx
Solución
i) S i F ( x ) = / * f ( t ) d t y u = u ( x ) , entonces
(F o u ) ( x ) = F ( u ( x ) ) = f ( t ) d t = G(x). Por laregla de la cadena, setiene
G'(x) = F '( u ( x ) ) . u '( x ) = F '( u ) . u ' = f (u). u ', pues F '( x ) = / (x ).
E n resumen, G '( x ) = / (u ).u '.
ii) H(x) = f “ f ( t ) d t = - / “ / ( t ) d t
Por (i), t f '( x ) = - ( / ( u ) . u ') = - / ( u ) . u '.
3 12 + 9 sen t + 15 ^
E je m p lo 26. S e a G (x ) = í — — -— —dt y W (x) = f
J_3 1 + 9 sen2t
Halle: a) G '( x ) b) t f '( x )
Solución
a) U sando el ejemplo 23-i), para / ( t ) = 1/(1 + 9 se n 21) y u = x 4, se tiene
1 4 x 3
C 'W = 3 - r ^ ------^ ‘ 4 x 3
l + 9 s e n 2(x 4) l + 9 s e n 2(x 4)
b) U sando el resultado del ejemplo 23-ii), obtenemos
. 1 , 3 x 2
H M = -----r — :-----r r — - • 3x
x 6 + 9 sen(x3) + 15 x 6 + 9 sen (x 3) + 15
124www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-131-320.jpg)
![rX*
INTEGRAL DEFINIDA
Ejem plo 27. Si G(x) = [ Ijl + y 3 d y,h alle G '(x ).
Jx2
Solución
C om o / ( y ) = ^/1 + y 3 es continua en M, entonces
G (x ) = f y i + y 3 d y = f ] l + y 3 d y + í X j l + y 3 d y
Jx2 ¿x2 Jo
Luego,
G '( x ) = - ¡ l + x * •2 x + V l + x 9 •3 x 2
= x [3x V i + x 9 - 2 3V l + x 6]
r 1 jx ld x
Ejem plo 2 8 . Calcule el v a lo r de -------- -
1 + x 2
Solución
Si / ( x ) = { ^ 2 ’ entonces / ( * )
1 + x 2 '
X
“ l + x 2
si x > 0
, si x < 0
Para calcular esta integral, se aplicará la propiedad aditiva respecto al intervalo de
integración. E n efecto,
f f ( x ) dx = f f ( x ) d x + f f ( x ) dx = = — i —l dx + í ■ * dx
J- 1 J - i J_x l + x 2 J0 1 + x 2
r l i° r l i 1
= - [ - l n ( l + x 2)j - l n ( l + x 2)]^
= ln 2) + | ( l n 2) = l n 2
Ejemplo 29. Calcule J = í |x2 + x — 6 |dx.
J~4
So lu ción
La variación de signos de x 2 + x - 6 = (x + 3 ) ( x - 2 ) es
+ - +
- 3 2
lu e g o |;t2 + x - 6 | = í A:2 + * _ 6 ' si x 6 ( - 00; - 3 ] u [2 ;+co)
i.uego, |x + x 6 | l _ ( x 2 + x _ 6 l s i x 6 < _ 3;2>
1 2 5www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-132-320.jpg)

![I . Kn cada uno de los siguientes ejercicios, calcule la derivada de las siguientes
(unciones.
INTEGRAL DEFINIDA
E JE R C IC IO S
..) /■
I»)
■'(x )- j co sh (2 t 2 + 1) dt
J
”Senx ^
------------dt
a arcsen t
C) f í [ y -— ^ — r d t ) dy
'2 J 8 1 + 1 + sen2t j *
d) F(x) =
•'a
R. F'(x) = 2 cosh ([8x2 + 1)
*■F 'w = Í t t A + sen2t
d t
r*3 1 j.
rJ0 i+ s e n 2t
eos2( y 2 + 4)dy
e) FQ t) = sen |J s e n ^J sen3t d t ] d y
2. Sean
/•arcsen^cosArj
F (x ) = / (se n t)dt -
A /3
J -s e n x ______ ____________
<Jg(t) dt = V i - . e o s x
sñ
J
1 — sen x
1 4- sen x
r f W dt
Halle H'(x) si H(x) = í ____
•'g(x)( 1- V l - x 2) ^
1 16
T '
/?. a = — 2 ó 1
f3 X + 1 2 / I
3. Si fCtjdt = ----- h a x ,calcule los valores de a de m odo que f -
JQ ax 4.
[ x* t s
4. Si F(x) — J ^ 1 + {4 dt , halle F'(x).
s X + X 2
5. Si G(x) = I 2 ~t2 d t , calcule G '(x ) y G '(l).
■>x2+i
r e*
6. Si F (x ) = I x ( t 2 + l) d t , calcule F '(x ).
7. Sea G(x) = I f ( t ) d t , donde f • 1 -* R es una función continua y las
•Vi(x)
funciones , <Pz'.]-*I, que son funciones derivables. Dem uestre que
G'(x) = f(<p2(x)) • <p'2 ( x ) - /O P iO O ) • < p 'i(x )
127
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-134-320.jpg)
![TOPICOS DE C A LC U LO - V O LU M E N II
8. Sea / : [ —!; 2] -> E una función continua. Si F es una antiderivada de / en
[-1 ; 2], con F ( - 1) = 3 y F(2) = 7, calcule J f(x)dx. R. 4
9. En la figura adjunta se muestra la gráfica de una función g. Si f es la función
definida por f ( x ) = J^gCOdt , x G [-3 ; 8], y t
Calcule gráficamente:
a) / ( — 3) b) / (O ) c) / ( 8 )
R. a) 0 b) 6 c) 34 -3 6 8
10. Sea /: [ - 6 ; 6] -> E una función continua y g: [ - 6 ; 6] ->
im par continua, tal que I / (x )d x = 10 y I g(x)dx = — 2. Halle:
J-6 “'-6
rO
una ¿unción
a) í t/(x) + £ (x )] dx fí. 12 b) [ [/(x) + s # ( x ) ] d x R. 20
•'-6 •'-6
11. En los siguientes ejercicios, calcule / (2 ) sabiendo que / es continua y
verifica la ecuación dada para todo x > 0 .
a) [ f { t ) d t = x 2( l + x )
Jo
b)
X2
í f ( t ) d t
■'O
x 2( l + x )
R. 16
2 + 3 V 2
r f W
c) I t 2 dt = x 2( l + x )
Jo
r X 2 {l + l)
R.
L
R. V 3 6
1
d) f f ( t ) d t = x
12. Dem uestre que si / es continua, entonces
J f ( u ) ( x - u ) d u = J ^ J f (t ) d t ^ j d u
Sug: considere F(x) = I f (u ) ( x - u ) d u , entonces F '( x ) = I f(u)du.
Jo Jo
Luego, halle su antiderivada y calcule F ( 0 ) para su constante.
13. A partir del ejercicio anterior, demuestre que
du[ Xf ( u ) ( x - u )2du = 2 f i f í f Zf ( t ) d t ) dz
Jo •'o lyo Jq J
128
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-135-320.jpg)
![14. H alle f ( x ) si = ■ 1 , V x > 0.
v i + se n 2*
15. Calcule el valor de las siguientes integrales:
a) J x 3 dx b) J (x + l ) 3 dx
f 1/2 1 r 2 x
c) I i d) ;------- 7 dx
Jo V i - x 2 Ji 1 + x
INTEGRAL DEFINIDA
e)
J-i 1+ 1*1 J3
i
5 5 x - 20
(2 - x ) ( x 2 + 1)
g) I | co sx| d x h) I se n 2(3 x )d x
Jo Jo
d x R. 1,336685 ...
ln x d x
r a! r
° L — i “* ° I
16. Sea / : [ - 6; 6] -» IR una función continua. Si f es im par y I f ( x ) d x = 3,
6
halle J (/ (x ) - 2x) dx. R. - 3 5
17. Para cierta población, suponga que N es una función continua tal que N(x)
es el número de personas que alcanzan la edad de x en cualquier año. Esta
función se llama función de la tabla de vida. Bajo condiciones apropiadas, la
integral J*+n N ( t ) d t da el número esperado de gente en la población que
tiene exactamente entre x y x + n años, inclusive. Si N(x) = 3 0 0 V 1 0 0 - x,
determine el número de personas que tienen entre 36 y 64 años.
R. 5 9 2 0 0 personas
18. Sea una recta tangente a la curva C : y = g ( x ) en el punto P (2 ;3 ).
Adem ás, la recta Lx pasa por el punto Q (1 0 ; 7) que no está en la curva C.
Si f ( x ) = J J t 2 + 7 d t , h a lle / '(2 ). R. 2
129www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-136-320.jpg)
![Teorem a 5. Si / es una función continua en / = [a; b] y si se reemplaza la
variable x de la integral por g { t ) (es decir, x = g(t)), donde g: [a;ß] -> / tiene
derivada continua en [a; ß], con g ( a ) = a y g ( ß ) = b ; entonces
TOPICOS DE CALCULO - VOLUMEN II
2.7 CAMBIO DE VARIABLE EN UNA INTEGRAL DEFINIDA
í f ( x ) d x = í f { g ( t j ) - g'(t)dt (17)
Ja Ja
D e m o stració n
ry
Sea F (y ) = í f ( x ) d x , y 6 I . Por el Prim er Teorema Fundam ental del Cálculo, se
Ja
tiene F '{y) = / (y ), V y 6 /.
Por la regla de la cadena ó derivada de una función compuesta, tenemos
í F í g m ' = F ' i m ) ■s '( t ) = / ( s e o ) •5 '( o
Por tanto, F ( g ( t )) es una antiderivada de f ( g ( t ) ) - g ' ( t ) . Por el Segundo
Teorem a Fundam ental del Cálculo, se tiene
C f ( f i( 0 ) •g ' W d t = [ F ( g m ß = F{g(ß)) - F( g(a)) = F (b ) - F (a )
•^a
= í / (x )d x
•'a
Observación 5. Si la función g [ a ß ] -* [a; b] es tal que g ( ß ) = a y g { a ) = b,
por lafórmula (17), se tiene
f f ( x ) d x = í f(gCO) ■g'{t)dt
Ja J ß
f3 x2
E je m p lo 31. Calcule I = I 3 3 dx.
J2 (1 + x )
So lu ción
Haciendo t = 1 + x 3, se tiene que x = g(t ) = V t - 1 , g'(t) =
3 V ( t - l ) 2 '
g( 9) = 2 y g ( 2 8 ) = 3. D ado que g y g' son continuas en [9; 28], entonces
I _ J2 ( 1 + a : 3)3 t _ J9 t3 2j(t —l ) z f
1 f 28 , l r l ]28
- j L -
’28 703
j9 381024
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-137-320.jpg)
![INTEGRAL DEFINIDA
Hn la práctica, no es necesario dar la función g ( t ) explicitamente. Considerando
que el lector está habituado a cambiar la variable en una integral indefinida, sólo
nos queda decir que para cambiar los límites de integración basta reemplazar la
variable original x por los límites de integración en la correspondiente sustitución
y así obtener los nuevos límites de integración (que son los valores de la nueva
variable). En el ejemplo anterior, procederíamos así:
C om o la sustitución es t = 1 + x 3, entonces d t = 3x 2dx.
Para x = 2 => t = 9 = a ; para x = 3 = > t = 2 8 = / ? .
Por tanto,
x 2 dx 1 r 3 3 x 2 dx 1 f 2Bdt 703_ x ¿ dx 1 r 3 3x ¿ dx 1 r 2
~ J2 ( 1 + x 3)3 ~ 3 J 2 (1 + x 3) 3 = 3 J9 t 3 3 8 1 0 2 4
f i (x^ — 1^dx
E je m p lo 32. Calcule el valor de 1 = I ---------------
•'1/2 (x2 + l ) V x 4 + 1
So lu ción
Antes de efectuar el cam bio de variable, dividim os numerador y denom inador por
x 2 ( x z > 0, pues x 6 [1/2; 1]) y luego reemplazam os t = x + 1/x. Entonces
_ f 1 ( x2 - l ) d x f 1 ( l - - p ) d x
Ji/2(x2 + l ) V x 4 + 1 J i/2 1 | 1
_ r 2 dt i /,ilNl2
- ' s / 2 í V t 2 - 2 V 2
, |f|aresee |—
V 2. 5/2
= - ^ ( a r c s e c ( V 2) - aresee^) = - aresee^)
V 2 V v 1 2) V 2
Eje m p lo 33. Demuestre que
a) Si / es continua en [0; a], entonces I f ( x ) d x = I f ( a - x ) d x .
Jo Jo
/*d r a.
b) Si fe s función par y continua en [-a ; a], entonces I / (x )d x = 2 I f ( x ) dx .
j-a Jo
c) Si f es función im par y continua en [- a; a], entonces I f ( x ) d x = 0.
•'-a
131www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-138-320.jpg)

![rXT/4
IN T EG R A L D E F IN ID A
f r M
1 = 1 In l + t a n í------- 6) I dd(aplicando el ejemplo 32 - a)
Jo 4
/■n/4 , l - t a n 0 f ^ 4 / 2
, = j0 ln V1 + lT tañfl) = i (íT ia ñ d )
rn¡ 4 /-rt/4
1=1 In2d0- I ln(l+ tanfl)c¡0
Jo ¿o________ __________ ,
i
/■ir/4 7r 7T
Por tanto, 2 1 = ln 2 d6 = - l n 2, de donde se concluye que I = — ln 2.
Jo 4 8
r Itx s e n x dx
E je m p lo 35. Calcule 1 = — —----— .
Jq 1 "i eos X
So lu ción
Teniendo en cuenta que e o s2x = 1 — se n2x, se tiene
r n x s e r ¡ x d x í 71 s e n x
1 = ------------— = x -----------dx
J0 1 + e o s2* J0 2 - se n 2x
sen x
Puesto que el integrando es de la form a x / (se n x), donde / (se n x ) = ^ _ ser)2' ~»
usando el ejemplo 32-e, obtenemos
rn s e n x n f n s e n x
1 = x - --------- - dx = — I ---------- 5- dx
J0 2 - se n 2x 2 J0 2 - sen2x
7T [ n Sen X 7T
= 2 Í = - 2 [arctan(coS* :'] 0
7T TTr 7T 7Tl 7T2 ’
= - - [a r c t a n (-l) - a rctan (l)]
2 L 4 4J
r^/4
<
-tt/4
r '■ 2
E je m p lo 36. Calcule J = (x 9 eos x + Vtan x + sen x e t o s I + eos2 x)dx.
J - n / 4
So lu ción
/•tt/4 r n / 4
J = ] (x 9 eos x + Vtan x + sen x e cos2jc)d x + cos2x dx
J — ir/4 J-7I/4
r^ 4 r 'r/41 + eos 2x
dx
/•TT/4 /-TI
j 2 - I co s2x d x = I
J —Í t l 4 *'-7
1 r sen 2x i'r/4 1 /7r re + 2
= ü b — L /. = í f e + 1 ) = —
133
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-140-320.jpg)
![E l integrando de es f ( x ) = x 9 eos x + V se n x + sen x e cos2* y es una
función impar, pues
TÓPICOS DE CÁLCULO - VOLUMEN II
/ ( - x ) = ( ~ x ) 9 c o s (- x ) + 7 t a n ( - x ) + s e n ( - x ) e cos2( x~>
= —x 9 eos x - V tan x - sen x e cos2x = - f ( x )
rn /i
Luego, p or el ejemplo 31 - a, se sigue que J i = f ( x ) d x = 0
J-n/4
n + 2 n + 2
P o r tanto, / = 0 H---------- = --------- .
2.8 I N T E G R A C I Ó N P O R P A R T E S E N U N A I N T E G R A L D E F I N I D A
Teorem a 6. Si u = u(x) y v = v ( x ) son funciones con derivadas continuas en
I = [a; b] , entonces
J u d v = [u v ]^ - J v du (1 8 )
D em ostración
De la diferencial de un producto se deduce que u d v = d (u v ) - v du.
r b r b r b r b
Luego, I u d v = I [ d ( u v ) - v d u ] <=> u d v = d ( uv ) - I v du
Ja Ja Ja Ja a
f *> . r b
=> u d v = [uv] - v du
•'a ® ■'a
(Todas estas integrales existen, pues u, v, u ', v ' son continuas)
E je m p lo 37. Calcule / = f x 2 lnx
'i
So lu ción
dx.
Haciendo
y =
^u = ln x => du = - d x
x o , obtenem os
A
dv = x 2 dx =» v = —
3
x 3 l3
■ j l n x - Í / ^ c Í A : = ( 9 |n3 - Í |n 1) - [ i ^
1 26
= 9 ln 3 — - (2 7 — 1) = 9 ln 3 — —
1 3 4www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-141-320.jpg)
![E je m p lo 38. Calcule el valor de J = j arctanJ^jx - 1 dx.
So lu ción
Si z = a r c t a n V V * — 1 => V * = se c2z => x = sec4z y dx = 4 se c4z tan z dz.
Para x = 1 => z = 0 y para x = 16 => z = tt/3. Entonces
rii/3
} = I z •sec4z tan z dz
Jo
Para integrar por partes a esta última integral, consideram os
f u = z => du — dz
-dv = 4 se c 3z •s e c z tan z d z => v = sec4z
Entonces
f *''3
7 = [z sec4z]o 3 — I sec4z dz (*)
Jo
j j . r^/3
— (—) (1 6) — I (1 + tan2z)se c2zdz
1Ó7T í tan3z n^
INTEGRAL DEFINIDA
•— tan z +
3 3
1Ó7T r-
= — - 2 V 3
0
(*) Para integrar sec4z es suficiente considerar que sec2z = 1 + tan2z.
2.9 I N T E G R A C I O N D E F U N C I O N E S D I S C O N T I N U A S
D e fin ición 6. Sea /: [a; b] -» IR una función acotada y sea P = {x0lxlt ...,xn}
una partición de / = [a; b]. Sean clt c2,...,cn elementos de /, de tal m anera que
Cj £ Ij Xyj , j 1/2, .../TI.
L a sum a
n
S ( / , P ) = £ / ( c , ) A ; x
;= i
se denom ina S u m a de R ie m a n n de f con respecto a la partición P.
Sean m ; = i n f { f ( x ) / x £ /,} y M¡ - su p { f ( x ) / x e 1¡}. Entonces
rtij < f ( c j ) < Mj, j = 1,2, ...,n y m ás aún
S ( / , P ) < S ( / , P ) < S ( / , P )
La sum a de Riem ann es un tipo de sum a que no necesariamente es una sum a
inferior o una sum a superior, sino m ás bien está com prendida entre ellas.
13 5www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-142-320.jpg)
![D e fin ición 7. Se dice que S(f, P ) tiene límite J e R cuando ||P|| —» 0 y se
escribe 5 ( / , P ) = / si dado e > 0 (arbitrario), existe 5 > 0 tal que para
toda partición P, con 0 < ||P|| < 8 , y para cualquier c¡ se tiene
m , P ) - ) < £
TÓPICOS DE CÁLCULO - VOLUMEN II
T eorem a 7 (de D a rb o u x). Si / es una función acotada en /, una condición
necesaria y suficiente para que f sea integrable en / es que exista / G IR tal que
Jim 5 ( / , P ) = / ; ( j = j j ( x ) d x ^
D e m o stració n (Ejercicio).
T eorem a 8. Sean f , g ■■l = [a ;b ] -» M dos funciones tales que f ( x ) = g(x),
V x E I, excepto para un número finito de puntos. S i g es integrable en /, entonces
/ es integrable en ¡ y se tiene
r b r b
í f ( x ) dx = í g(x)dx (1 9)
Ja Ja
D e m o stració n
S i g es integrable en / y g { x ) d x = J, por el teorema de Darboux, dado e > 0,
existe 8X > 0 tal que para todo P, con 0 < ||P|| < 5 1; y V c¡ E l¡ se tiene
S { g , P ) - J < £-
Por otro lado, si A = {x e / / f ( x ) * g ( x ) } posee r puntos (r finito) y sea
L = s u p { f ( x ) - fl(x)| / x E /}, para toda partición P, con ||P|| < , se tiene
S ( f . P ) - S ( g , P ) l = < r L P -
2rL 2
Luego, si 8 = mín|<51( se tiene
IS(f. P ) - ] < m , P ) ~ S(g, P ) |+ 15(5 ,P ) - J | < | 1 = £
E n resumen, para toda partición P, con ||P|| < 5, y V c¡ E / se verifica
S ( f , P ) - J < E
Por tanto, por el teorema de Darboux, / es integrable en / y
f f ( x ) d x = í g(x)dx
J a J a
1 3 6www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-143-320.jpg)
![I roi cm a 9. Si / es continua en / = [a;b] excepto en ios puntos a ó b, en los
mi.îles existen lim< / ( x ) = / ( a + ) y lim f ( x ) = f ( b ~ ) (finitos), e n to n c es f es
j:-*b~
iiiii-i'.iahle en / y existe una función F, con F'(x) = / (x ), V x E (a; b), tal que
■b
f ( x ) d x = F { b ) - F ( a )
IN T EG R A L D E F IN ID A
f■Jn
Dem ostración. Ejercicio para c! lector.
D efinición 8 (F u n c ió n seccionalm ente continua en l ~ [a ;¿]). Se dice que la
lim dón /: / -> 1 es seccionalmente continua en / cuando / es continua para todo
' / excepto para un número finito de puntos c¡ , j = 1 , 2 m , para los
i nales existe
f ( c ~ ) = lim_ f ( x ) y f ( c f ) = l i m / ( * )
x ' * ci x ~,cj
‘.i i) - a a c¡ = b, debe existir / ( a + ) o f ( b ~ ) respectivamente.
r O K O L A R I O . Si / es seccionaimente continua en / = [a;b], entonces / es
mu-arable en /.
í - 2 , si - 2 < x < - 1
I jcm plo 39. Sea la función / ( x ) - ] x 3, si - 1 < x < 1 .
( 2 , si 1 < x < 2
Sr pide:
.i) I race la gráfica de /.
Ii) ;,/ es integrable en [— 2 ; 2 ]?
i ) Calcule I f(x)dx.
J-2
il) Halle F ( x ) = f f ( t ) d t , x £ [ - 2; 2] y trace su gráfica.
J-2
i ) Determine el conjunto donde F es derivable y halle F '(x ).
Solución
,i t I a gráfica de / se muestra en la Fig. 2.15.
I>) / es integrable en [— 2 ; 2]porque / es seccionalmente continua en [— 2 ; 2]
(/' es discontinua en x = - 1 , en x = 1 y en x = 2 ;pero en estos puntos
existen los límites laterales. E n x = 2 existe el límite lateralporizquierda).
i ) í f ( x) dx = f f ( x ) dx +í f ( x) dx + f f ( x ) dx
J -2 ■J-2 J-l •'1
= í ( - 2)d x + í x 3d x + í 2 d x = - 2 + 0 + 2 = 0
J-2 ■'-1
137www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-144-320.jpg)
![TOPICOS D E C A L C U L O - V O LU M E N II
d) Si x e [-2 ; -1 > => F (x ) = f ( - 2 )dt = - 2 x - 4
J-2
Si x E [—1,1] =* F (x ) = J f ( t ) d t = J ( - 2 )dt + J t
Si x E (1; 2) =* F(x) = J f ( t ) d t —J (— 2)dt + J t 3 dt + J 2 dt = 2x —4
t 3 dt = ■
x 4 9
T _ 4
í - 2 x - 4 , - 2 < x < - 1
Por tanto, F ( x ) = | (x 4 - 9 ) / 4 , - 1 < x < 1
2 x - 4 , 1 < x < 2
La gráfica de F se muestra en la Fig. 2.16.
í —2 , - 2 < x < —1
f) F'(x) = x 3 , — 1 < x < 1
i 2 , 1 < x < 2
Luego, F es derivable en [— 2; 2) excepto en los puntos x = —1 y x = 1.
Fig. 2.15
F(x) = f 2te~cZ
Jo
d t , x e R.E je m p lo 40. Trace la gráfica de
Solución
i) D(F) = E
ii) Intersecciones con el eje x: P ( 0; 0), pues F ( 0) = 0.
iii) F '( x ) = 2 x e ~ * 2. E l único punto crítico es x = 0 y se tiene
Signo de F'(x) < - +
Luego, F es creciente en (0; +oo) y F es decreciente en (— oo; 0>. E l valor
m ínim o relativo es F ( 0 ) = 0.
138
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-145-320.jpg)
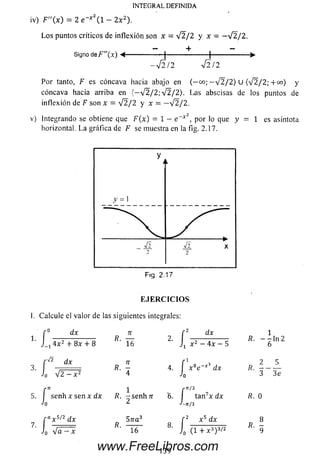

![cn eos x f ^ 2sen x c o sx
Si I 7— — --; 7 dx = A, calcule el valor de la integral --------------- dx en
h (x + 2 )2 J0 x + 1
función de A. R - ( - 4 ------ -------
2 2 n + 2 )
f n c o s x d x [2 c o sx f 71e o sx dx
Sugerencia: exprese ¿ J,
Luego, calcule cada una de las dos integrales usando integración por partes y
finalmente haga el cam bio de variable x = 2 u.
f 1 e x
III. Si k = I dx, exprese los valores de las siguientes integrales en función
J q X T i-
de k.
'• l - , 7 ^ T T dx ~*ce~a <Sug: u = a —x — 1)
IN T EG R A L D E FIN ID A
? f 1 x e x¿
J0 x2 + 1
s. f -
Jo I
dx
e x 1
dx /?. k + 1 - - e
(x + 1 )2 2
4. í e * l n ( l + x ) fi. e l n 2 - f c
Jo
IV . Ejercicios diversos.
1. C alcular/(O ) sabiendo que / ( n) = 2 y f [/(x) + f"( x)] senx dx = 5.
Jo
R. 3
[ bs enx cosa eos b f b c o sx
2. Pruebe que ------- dx = -----------------— + — -- d x .
Ja x a b Ja x 2
Í 12x — 12 , si x < 1 , . f 2*
3. Si / (x ) = _ s i x > 1 : 3 (1 ) = ^ m d t , X E R .
Calcule el valor de f g( x)dx. R. 3 6 9 7 / 4
2
4. Si n es cualquier núm ero natural, calcule el valor de
r^ se n (n + j ) x
J x
sen 2
-dx /?. 7T
141www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-148-320.jpg)
![TOPICOS DE CALCULO - VOLUMEN II
5. Calcule el valor de las siguientes integrales:
-1' 2 f l + X
a) Jcos(sen x ) In — - J + 3x + 4
r n / 2
b) I x sen x dx
-'-71/2
çn/2
c) I x 81c o s(x 9) dx
J-ji/2
/•tt/4
d) I [x14se n (x 7)] dx
J-nj
dx
TI¡A
e) f [(x 5 + x 3 + x ) V l + x 4 + 3j dx
J - 7
R. 4
R. 2
R. 0
R. 12
6 . Sea /: 1 una función continua. Si se sabe que í f ( t ) d t = 6 ,
•/-i n
calcule
f / ( 2x — 2) dx.
J — 4
7. Sea / ( x ) =
si 0 < x < 2
- 1 , si 2 < x < 3
. x - 3 , s i 3 < x < 4
a) Esboce la gráfica de /.
b) Calcule JQ4 / (x )d x .
c) Calcule F ( x ) = f * f ( t ) d t , x G [0;4],
d) Trace la gráfica de F.
e) Determ ine en qué puntos F es derivable.
8 . Sea F (x )
f * e‘2
= ^------ ? d í-
J0 1 + t2
a) Pruebe que F es función impar.
b) Pruebe que F ( x ) > x ,V x 6 i j = [0; +oo).
9. Calcule el valor de
çtt/3
L * 1
Veos X
n/6 V se n x + V c o s x
dx.
10. La ecuación param étrica de una curva es H
h ;
co sz
dz
sen z
, t > 1. Halle
-dz
d y
dx '
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-149-320.jpg)
![INTEGRAL DEFINIDA
11. La función / y su inversa / _1 son continuas y / (O ) = 0. Pruebe que
-5 r f ( 5)
/ ( x ) d x + f ~ 1( t) d t = 5 / ( 5 )
-'o •'o
dx
12. Calcule el valor de
r 3
13. Calcule el valor de
-3
r
i
(2x 2 + l)^/x2T í '
x 2 - 4
f A - T
14. Calcule el valor de I 7-^— 7-71dx.
x 2 - 2 5
3 x 2 _ 4
3 I* 2 - 1 6 1
dx.
15. Sea / una función continua tal que / '( x ) < 0 en [1; 4].
Si / ( 1) = —2 , / ( 4 ) = —6 y J14 / ( x ) d x = —10 , calcule el valor de
f f ~ 1( x)dx. R. 12
J-f,J-6
x < 2
16. Si / ( x ) = j ’^2 ^ X < ° , calcule J [/ (x) - x]dx.
-1 + x 3
x > 0
r271
17. Calcule I (|sen x| + x)dx.
•'O
{ e2- l
18. Calcule f [4 - 2 ln (x + 1)] dx. R.'2 (e 2 - 3)
•'O
f5|x3 -
■'-1
19. Calcule |x3 - 4 x | d x .
d x 15?r + 44
Calcule — =— — 7 . R.
(x 2 + l ) 4 96
/ * sen(t — l ) 2 dt 1
.’.l. Calcule lim -------—-------— ------ .
*-1 (1 — x ) 3
cn/2 dx n
Calcule ------- ---------p . R. —
J0 1 + f t a n x ] ^ 4
Sugerencia: hacer u = - —x.o 2
143www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-150-320.jpg)
![TÓPICOS DE C Á LC U LO - V O LU M E N II
Para calcular una integral definida por la fórmula de N ew ton-Leibnitz se necesita
hallar una antiderivada del integrando; pero en el capítulo I hem os m encionado
que no toda función continua tiene una antiderivada expresada mediante funciones
elementales, por lo que es necesario los métodos aproxim ados para su cálculo. En
esta sección tendremos en cuenta que, por el teorema de Darboux,
I f ( x ) d x = ||Hmo ^ / ( t , ) A ¿ x , donde P = {x 0, x 1(
“ i= i
es una partición de [a; b] , A ¡x = x¡ —x ^ y t¡ 6 [xi_1; xi],
2.10.1 A P R O X I M A C I Ó N P O R R E C T Á N G U L O S
Sea /: [a; b] -> E una función continua.
Sea P = [x0 = a , x 1, x 2, ...,xn = b} una partición de [a; b] de tal manera que el
intervalo [a; b] quede dividido en n partes iguales. L a longitud de cada uno de los
subintervalos es
b - a
Ax = --------
n
S ea y¿ = /(* ,-), i = 0 , 1 , 2 ,..., n.
Cada una de las sum as
y 0Ax + y xAx + y 2Ax + ... + y n. xAx
y xAx + y 2A x + y 3A x + ... + y nA x
expresa aproximadamente la integral
í f ( x ) d x
Luego,
[ f ( x ) d x s A x ( y 0 + y ! + y 2 + + y,,^!) (2 0 )
Ja
í f ( x ) d x = Ax ( y x + y 2 + y 3 + - + yn ) ( 2 1 )
Ja
Teniendo en cuenta que y kAx es el área algebraica del rectángulo debase A x y
altura y k, en la figura 2.18 se muestra el polígono rectangular cuya áreaalgebraica
es la aproxim ación del valor de /a&/ ( x ) d x usando la fórm ula 19.
E l error que se comete al calcular el valor de la integral por la fórm ula de los
rectángulos (19) ó (20) es m enor cuanto m ayor es el número n.
2.10 CÁLCULO APROXIMADO DE LAS INTEGRALES DEFINIDAS
144
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-151-320.jpg)
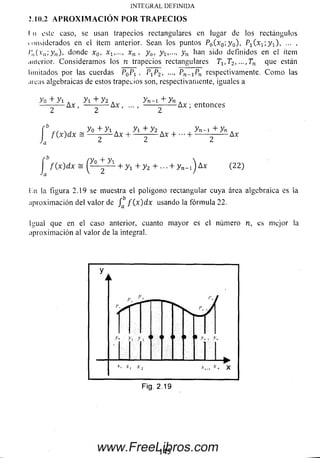
![P rop osició n 5. Sea g( x ) = A x 2 + Bx + C , donde x 6 [a; b ] , y 0 = g ( a ) ,
( a + b
yi = s ( — 2~ J ' y 2 = 9 Entonces
A x , b — a
TÓPICOS D E C Á L C U L O - V O LU M E N II
2.10.3 APROXIMACIÓN POR PARÁBOLAS (FÓRMULA DE SIMPSON)
/* Ax
I G4x2 + B x + C )d x = — [y0 + 4yt + y 2] , donde Ax
Ja ^
D em ostración
Por el segundo Teorem a Fundamental del Cálculo,
rb
(.Ax2 + B x + C )d x =
(23)
Ax3 Bx2
~ T + ~ + C *
Luego de efectuar las operaciones indicadas se demuestra que
fb Ax
j (Ax2 + B x + C)dx = — [y2 + 4 y 1 + y 0].
Considerando esta proposición, si la parábola y = A x 2 + Bx + C pasa por los
puntos
/a + b
P0(a-,y0) , Pi 2~ ¡ y i ) ■ p2(b;y2) .
entonces el área algebraica bajo la parábola está dada por (23).
Sea f una función continua en [a; b]. Para hallar una aproxim ación de f ( x ) d x ,
la idea básica es aproxim ar la gráfica de f por arcos de parábolas. Para
dividim os el intervalo [a; b] en n partes iguales, donde n es par. Sean
{x 0,x 1,x 2, ...,xn } los extremos de los subintervalos, y y¡ = / (x ¡), i = 1,2 , ...,n.
E l área algebraica bajo la parábola que pasa por los puntos (x 0; y 0), ( x ^ y - J
Y i x2; y 2) está dado por ( y 0+ 4 y 1 + y 2)A x/3 . A s í m ism o, el área algebraica bajo
la parábola que pasa por los puntos (x 2; y 2), (x 3; y 3) y (x 4; y 4) , está dado por
(y 2 + 4 y 3 + y 4)A x / 3 y así sucesivamente, hasta llegar al área algebraica bajo la
parábola que pasa por los puntos (x n _2; y n_ 2) ' ( X i - n 'y n - i X (x n ;y„ ) está dado
por (y n- 2 + 4 y n _! + y n)A x/3 .
Por tanto,
f b Ax „ A x , . Ax
J f{x)dx = — (y0 + 4 y x + y 2) + — (y2 + 4 y3 + y4) + + — (y„_2 + 4 yn_1 + yn)
f ^ Ax
J f(x)dx s — [(y0 + yn) + 2 (y2 + y4 + ... + y n_2) + 4 (y t + y 3 + ... + y n- i)] (24)
Esta fórm ula es llamada fó rm u la de Sim p son .
146www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-153-320.jpg)
![INTEGRAL DEFINIDA
Ejem plo 41. Para n = 10, calcule por aproxim ación el valor de
"1 4 dxf 1 4 dx
J0 1 + X 2
Solución
Si n = 16, entonces Ax - (1 - 0 )/ 1 0 = 0,1.
x í
f ( x _ 4
x i / (*« )' C 1 + x 2
o
il
o
X
O
(i1
4*1
O1 X (y = 0 ,6 y 6 = 2 ,9 4 1 1 7 6 4 7
x i = 0,1 y x = 3 ,9 6 0 3 9 6 0 4
1!
o
Vj
y 7 = 2 ,6 8 4 5 6 3 7 5
x 2 = 0,2 y 2 = 3 ,8 4 6 1 5 3 8 4
*co
II
O
00
y 8 = 2 ,4 3 9 0 2 4 3 9
x3 = 0.3 y 3 = 3 ,6 6 9 7 2 4 7 7 x9 - 0,9 y 9 = 2 ,2 0 9 9 4 4 7 5
x4 = 0,4 y 4 = 3 ,4 4 8 2 7 5 8 6
T“l
II
O
*
o
II
NJ
O
x 5 = 0,5 ys = 3,2
Por la fórm ula (20) (aproxim ación por rectángulos),
í 1 4
7 T T T dx = 0, í [y0 + Vi + y 2 + ■■■+ y 9] = 3 ,2 3 9 9 2 5 9 8 9
-'o + x
Por la fórm ula (21) (aproxim ación por rectángulos),
-i 4
f 4
i Í T ^ dX - 0,1 [}>1 + y2 + ■■■+ y 9 + y io ] = 3 ,0 3 9 9 2 5 9 8 9
Por la fórm ula (22) (aproxim ación por trapecios),
4
--dx = 0,1
í r
= 3 ,1 3 9 9 2 5 9 8 9
+ x 2
Por la fórm ula (23) (aproxim ación por parábolas o método de Sim pson),
f 1 4 0,1 r
J i + x z dx ~~3~'-y° + y i ° + 4(-y i + y 3 + y s + y ? + y ^ +
+ 2 ( y 2 + y 4 + y 6 + y 8)] = 3 ,1 4 1 5 9 2 6 1 4
Este últim o valor com parado con el valor real de la integral
"1 4 dx
= n = 3,14159265..
í0 1 + * 2
es exacto hasta la séptima cifra decimal.
1 4 7www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-154-320.jpg)

![3ti*
<......... 1- ...................... • " ^
INTEGRALES
IMPROPIAS
En la definición de la integral definida í f { x ) d x , fueron establecidas ias dos
Ja
restricciones siguientes:
I o El intervalo / = [a-,b] es acotado
2 o / es acotada en /D
Ahora trataremos de librarnos de estas restricciones, extendiendo el concepto de
integral definida al caso en donde el intervalo de integración es infinito o el caso
en donde la función del integrando / presenta discontinuidad infinita en [a; b].
Las integrales que tienen estas características se llaman integrales im p ro p ia s y
son de dos tipos:
T ip o 1: Integrales im propias con límites infinitos.
T ip o 2: Integrales im propias con límites finitos (con discontinuidades infinitas).
3.1 I N T E G R A L E S I M P R O P I A S C O N L Í M I T E S I N F I N I T O S
D efinición 1. Sea / :/ = [a ;+ o o ) -* R una función continua en el intervalo /.
La integral impropia de / de a a +co se denota y se define como
í f ( x ) d x = lím f f ( x ) d x
Ja t~’+' Ja
r+CO
Se dice que la integral im propia I f {x)dx c o n v e rg e cuando el límite existe.
•'a
Si el límite no existe o es infinito, se dice que la integral im propia diverge.
Observación 1. Como vimos en el capítulo anterior, si f (x) > 0 , la integral
definida I f ( x) dx representa el área de la región plana limitada por
la gráfica de f , el eje x y las rectas verticales x = a y x = t. Luego, cuando Ia
integral impropia es convergente podemos interpretar que el valor de la integra!
es el área de la región plana infinita que se encuentra a la derecha de la recta
x = a y está comprendida entre la gráfica de f y el eje x (Fig. 3.1).
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-156-320.jpg)
![TÓPICOS DF C A I C U I.O - VOI I'M F N II
Fig. 3.1 Fig. 3.2
D efinición 2. Sea /: / = (— °°;b] -» R una función continua en el intervalo /.
La integral im propia de / de — oo a a se escribe y se define com o
" b r b
í f ( x ) = l‘m í f { x ) d x
J—00 t-»-00 J
Si este límite existe, se dice que ¡a integral impropia es convergente; en caso
contrario se dice que es divergente.
Por otro lado, si f ( x ) > 0, V x e / y la integral im propia I f { x ) d x converge,
j — 00
entonces elvalor de la integralrepresenta el área de la región plana infinita
ubicada a izquierdade la recta x = b y está limitada por la gráfica de. / y el eje x
(Fig. 3.2).
D efinición 3. Sea /: E -* K una función continua en el intervalo {-o o ;+ c o }.
La integral im propia de f de — oo a + co se escribe com o
r + 00 f b r + co
I f ( x ) dx = I f ( x ) dx + I f ( x ) dx
J — 00 J —OO J b
donde b es cualquier número real.
,.+ 0 0 r b
La integral im propia f ( x ) d x es c o n v e rg e n te si tanto I f ( x ) d x como
J —00 —00
í
/ (x ) dx son convergentes, y es d iv e rg e n te si alguna de las integrales
impropias del lado derecho diverge.
E je m p lo 1. Determ ine si la integral | (x - 2) exdx converge o diverge.
J-00
Solución
En esta integral se aplica la integración por partes con u = x — 2 y d v = e xdx.
150www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-157-320.jpg)
![INTEGRALES IMPROPIAS
De la definición de la integral impropia, se tiene
[ (x - 2 ) e xdx = lim f (x - 2) e xdx = lim [(x - 2 ) e x- e x]2
■Leo t-f-CO Jt t->-CO t
= lim [ - e 2 - (t - 2 ) e t + e c] = - e z - lim (t - 2 ) e c
t —*—oo
El últim o límite es de la form a 0. Aplicando la R egla de L ’Hópital, se obtiene
0
t - 2 1
lim (t - 2) e c = lim — — = lim -----
t-*—oo t -+—co Q 1 t-» -c o —Q~
Por lo tanto, concluim os que
r 2
(x - 2) e xdx = - e 2
fJ — (
En conclusión, la integral im propia es convergente y converge a — e 2.
r+°° ^ _j_ 2X
E je m p lo 2. Determ ine si la integral —— — — - d x converge o diverge.
x "f- 3x 5
So lu ción
+0° x 2 4- 2x
i x 3 4- 3 x 2 4- 5
dx
i r +0
lim -
t->+cc 3 J1
3x2 + 6x 1 t
d * = x lim [ln x 3 + 3 x 2 + 5|]
x 3 + 3x2 + 5 3 t-*+oo J1
1 1
— lim [ln|t 3 4- 3 t2 4- 5| - ln 9] = ~ ( + o o ) = + o o
3 t-»°° 3
Por tanto, la integral im propia dada diverge.
r+ CO
E je m p lo 3. Calcule -------- rd x .
L o o 1 + X 2
Solución
Eligiendo b = 0 , se obtiene
r +0° dx _ r° d x r +co
J_00 1 + X 2 ~ J_!x¡1 + X 2 + Jg 1
' r° dx f b dx
= lim -------7 + lim ------- 7
a->-oo J 1 + X 2 b-*+oo J 1 + x 2
dx
+ x 2
.y =
1+ x2
Fig. 3.30 b
= lim [arctan x] 4- lim [arctan x]
a-> -°O a b-*+co o
= lim [arctan(a)] 4- lim [arctan(b)] = - ( — rr/2) 4- n/ 2 = n
a->-co ö-»+oo
[ +°° dx
Por lo tanto, la integral im propia I ------- - es convergente y converge a n
J-oo i + x l
1
En la Fig. 3.3 se m ue stra la gräfica de f ( x ) = + x 2 ■
151www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-158-320.jpg)
![TÓPICOS DE C Á LC U LO - V O LU M E N II
f ax
E je m p lo 4. M uestre que la integral I — converge si p > 1 y diverge si p < 1.
J x^
f cdx _
J i xp ~ —p + 1
Solución
Para p 1, se tiene que
Luego,
C+codx f
a) Si p > 1, — = lim
XP t^ +QO
y la integral considerada es convergente.
/•+cod x r Édx t 1'?
b) Si p < 1, I— = lim — = lim
Jjx p + x p +°
y la integral considerada es divergente.
rt dx
— = lim
XP Í-.+CO
1
(1 - P ) t p -1 1 - p . p - 1
1 - p 1 — p
= : 4-00
c)
f +” dx r £dx
Si p = 1 , I— - = lim I — = lim [ln
Jj XP t->+co X t-*+00
y así la integral dada es divergente.
t] = + C
En resumen.
■/; xP
es convergente si p > 1 y divergente si p < 1.
3.2 I N T E G R A L E S I M P R O P I A S C O N L Í M I T E S F I N I T O S
D efinición 4. Sea /: I-» R (donde I = [a; ó » una función continua en / y
lim / ( x ) = co. La integral im p ro p ia de / de a a b se define com o
x-*b
f f ( x ) d x = lim í / ( x ) d x
Ja t-*»' Ja
Si ellímite existe, se dice que laintegral im propia es convergente; encaso
contrario se dice que es divergente.
L a definición dada también es equivalente a
r b r b - E
I f { x ) d x = lim I / ( x ) dx
Ja E" 0+ Ja
Si/ (x ) > O, V x £ [a ; b ], y la integralim propia I/ (x ) d x esconvergente, el
valor de esta integral representa el área de la región infinita lim itada por la gráfica
de /, el eje x y las rectas x = a A x = b (Fig. 3.4).
152www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-159-320.jpg)
![INTEGRALES IMPROPIAS
a t
Fig. 3.5
D efinición 5. Sea /: / -* E (donde / = (a; b]) una función continua en / y
Jim / (x ) = oo . La integral im propia de / de a a b se escribe com o
f f ( x ) d x = lim í / (x )d x
Ja a A
Si el límite existe, se dice que la integral im propia es convergente; en caso
contrario se dice que es divergente.
La definición dada también es equivalente a
r b r b
I f ( x ) d x = lim I f ( x ) d x
Ja e~>0 Ja+e
Si / (x ) > O, V x e [a; ¿] y la integral im propia I / (x ) dx es convergente, el valor
de esta integral representa el área de la región infinita limitada por la gráfica de /,
el eje x y las rectas x = a A x = b (Fig. 3.5).
Definición 6. Sea f: I -» E (donde / = [a; £>]) una función continua en /,
excepto en algún punto d G (a; b) en donde lim / (x ) = o o ó lim / ( x ) = oo.
x-*d+
Entonces se define
f f (x ) d x = í f ( x ) d x + í / (x )d x
•'a •'a Jd
r b f d r b
l.a integral im propia I f(x)dx es convergente si tanto I f(x)dx com o I f(x)dx
ja 'a Jd
son convergentes, y es divergente si alguna de las integrales im propias del lado
derecho diverge.
153
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-160-320.jpg)
![Observación 2. Si la función f definida en (a; b) (a puede ser —oo y b puede
ser + 00) tiene dentro del intervalo (a; b) un número finito de puntos de
discontinuidad infinita c1(c2, ....,cn , entonces la integral de la función f en
(a; b) se define como
f f ( x ) dx = f f ( x ) d x + f f ( x ) d x + . . . + f f ( x ) dx
•'a *a *Cx cn -i
siempre que cada una de las integrales impropias del segundo miembro sean
convergentes. Si por lo menos una de las integrales diverge, entonces
f b
I f ( x ) dx también diverge
Ja
f 2 dx
E je m p lo 5. Determine, si existe, I —
J1 V x - 1
Solución
1
La función / ( * ) = — .- es continua en (1; 2] y lim f ( x ) = + 00.
Luego,
/ = [ = lim í = lim Í2V x - 1 ]2 = lim Í2 - 2V t - 1 1 = 2
Por lo tanto, la integral im propia / es convergente y converge a 2.
f 1dx
E je m p lo 6 . M uestre que la integral I — converge si 0 < p < 1 y diverge si
Jq x
p > 1.
So lu ción
a) Para 0 < p < 1, nos queda
TOPICOS DE CALCULO - VOLUMEN II
[ v d x f 1 dx
— = lirn —- = lim
J0 xP t-*o+Jt x p t->o+
t i - P
1 - p 1 - p
y la integral considerada es convergente.
1 - p
f * dx f * dx
b) Parap = 1 , I — = lirn — = lim ( - ln t) = +00
J0 x t-*o+ x t-o+
y la integral dada es divergente.
[ ' d x f 1dx 11
c) Parap > 1 , I — = lim I — = lim
J0 x pt-»o*Jt xP t-o+( p - l ) t P - 1 p - 1
+00
y la integral es divergente.
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-161-320.jpg)
![INTEGRALES IMPROPIAS
/■*/«
Ejemplo 7. Calcule, si existe, la integral I cot 9 d.6.
■'-fr/4
So lu ción
Se observa que la función / (fl) = cot 6 = tiene discontinuidad infinita en
sen 8
9 = 0. A si, la integral dada se escribe como
r*r/ 4 r 0 rít/ 4
I cot 8 d.8 = i c o t 9 d8 + cot 8 d8
J - n/4 J-n /4 Jo
Puesto que la integral
í cot 8 dd = lim í cot 8 d8 - lim [ln|sen 0 |] I l M
J —n / 4 e - 'O + J - n / 4 ^ 0+ '
- J[im+ [ln|-sen(e)| - ln ( V 2 / 2 )] = -o o
es divergente, entonces la integral dada también es divergente
r o e i/x
Ejemplo 8. Calcule I — j~dx (si existe).
J x
So lu ción
C
La función f ( x ) = — tiene discontinuidad infinita en x = 0. Entonces, usando el
x
método de integración por partes, se obtiene
r0 gl/X f - £ p i/x r -1
' ■ - 1 ■ - [ei / * _ _ ei/*l
X
2
r e f ~ £e 1/x r
— z -d x = lim I — j - d x = lim e
J_! Ï 3. £->0+J_! X3 £->0+1
— lim + - e _1/£ - 2 e '
£-*0+ L £
e _1/£ 0
NOTA: El limite Um+ — -— es de la form a - . Aplicando la Régla de L’Hôpital,
résulta
e -1/£ 7 - l / e 2 î
lim ,--------= lim — T7- = l i m -------------r-4 = 0
£-♦0
i — u n i — t t = n m -------------2—* ■
+ e £-*o+ e1'* £-*0+ei/£^_
+00
dx
Ejemplo 9. Calcule, si existe, I
J - c o ¿ )
Solución
La función / (x ) = — — — tiene discontinuidad infinita en x = 0 y x = 2.
x{x - 2) 3
E ligiend o los puntos * = - l , x = l y i = 3 , la integral dada se escribe
155
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-162-320.jpg)





![INTEGRALES IMPROPIAS
'•+00 dx
52. Si G (a ) = ^ - + x a ) X( 1 + x 2 ) . calculeG (0), G ( 1), G(2).
/?. 7t/4 ; nr/4; tt/4
f +°°senx tí f +0° se n 2x
53. Sabiendo que I ------- d x = — , calcule el valor de I — r — dx.
J0 x 2 J0 x 2
R. n /2
54. Esboce la gráfica de la función F (x ) = I f ( t ) d t en los siguientes casos:
J — 00
si |t| > 1
( 1 , si t < 1
b) m = | i
2 , Si |t | > 1
55 Sea f ( x I - í™ ** ’ SÍ |x| ~ 355. Sea / ( x ) - ^ si W > 3
f+co 1
Determ ine m de m odo que I / (x )d x —1. R. m = —
J-œ 18
3.3 I N T E G R A L E S I M P R O P I A S C O N I N T E G R A N D O S N O N E G A T I V O S
P rop osició n 1. Sea / una función no negativa en [a ; b ) (esto es, / ( x ) > 0) e
integrable en [a; t] para todo t 6 [a; b).
Si la función F (t) = I / ( x )d x es acotada en [a; £>), entonces I / ( x )d x converge.
•'a Ja
D em ostración
Com o / (x ) > 0, V x £ [a; fe), entonces F (t) = I / (x )d x es creciente en [a; 6).
Ja
Por hipótesis, F ( t ) es acotada. Entonces F ( t ) es creciente y acotada en [a; b).
Por tanto, lim_ F (t ) existe y es finito, es decir, I / (x )d x es convergente,
t— /•'a
161www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-168-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
Proposición 2 (C riterio de Com paración)
Sean / y g funciones tales que 0 < / ( x ) < g(x), para todo x e [a;b), e
integrables en [a; t], V t e [a; b). Luego,
a) Si I g(x)dx converge, entonces I / (x )d x converge.
•'a “'aJa
b) Si I f(x )d x diverge, entonces s ( x ) d x diverge.
•'a *'a
Demostración
Se sigue inmediatamente de la proposición 1 y de la desigualdad
í f(x ) d x < í g (x )d x , V t 6 [a ;b)
•'a ■'a
f +0° dx
Ejemplo 11. Verifique si J 4^ "i converge o diverge.
Solución
1 1 r , f +codx
Com o 0 < ----- < — , Mx £ [2; + 00), y— - es convergente (ver
h x 6
dx
2 x - V l + :
'2
f +°° dx
ejemplo 2, p = 6), entonces se concluye que J ——j = = = es convergente.
f 1 dx
Ejemplo 12 . Analice el com portam iento de la integral , = .
Jo V x 2 + 2x
Solución
1 1 , , f 1 * ' ,
Com o 0 < - < - = , V x £ (0; 1], y - p es convergente (ver ejemplo
V x 2 + 2x V x Jo V x
f 1 dx
4, p = 1/2) , se concluye que es convergente.
Jo V x 2 + 2x
f -3 dx
Ejemplo 13. Verifique si . „■= es convergente o divergente.
V x 2 + 3x + 2
r 3 dx
i-o, V x 2 + 3x + 2
Solución
I
1 1 f 3 d x
- <
x V x 2 + 3 x + 2
3 dx
í dx
Com o 0 < — < — - , V x £ ( - 00; - 3 ] , y ---------------------- diverge, entonces
j -00 *
Vx2 + 3x + 2
es divergente.
162www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-169-320.jpg)
![rb
IN T EG R A LES IM PR O PIA S
Definición 7. Se dice que la integral impropia f f ( x ) dx es ab solu tam en te
b
convergente cuando I |/(x )|d x es convergente.
Ja
Proposición 3. Si la integral I /(x )d x es absolutamente convergente,
Ja
entonces es convergente.
Demostración
Como 0 < |/(x )| — f ( x ) < 2 |/(x )| , se sigue, por la proposición anterior, que
l / M I —/"(■*) es convergente. Luego,
r b r-b r b
I /(x )d x = I |/(x )|d x — I [|/(x )| - /(z )] dx converge
Ja Ja Ja
f +coCOS O 2)
Ejemplo 14. Analice sí I -------— dx es convergente o divergente.
Ji x
Solución
La integral dada es absolutamente convergente, pues
eos (x 2) 1 r * f +c°d x
< — , V x e [1 ;+ c o > , y la integral — es convergente.
* Ji x
f +° ° c o s ( x 2)
Luego, por la proposicion anterior, I ----- -— dx es convergente.
Jl X
Proposición 4 (Criterio del Límite)
Sean / y g funciones no negativas integrables en [a; t], V t 6 [a; b), y
supongam os que
m
lim — — = r .
x-*b- g(x)
i) Si 0 < r < +oo, entonces las integrales im propias •
F = í f W d x y G = í g (x )d x
Ja Ja
son ambas convergentes o ambas divergentes.
b) Si r — O y G converge, entonces F converge.
c) Si r = ±oo y G diverge, entonces F diverge.
Demostración, (ejercicio para el lector).
163www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-170-320.jpg)
![C o ro la rio 1. Sea f una función integrable en [a; t ] , V t G [a; + 00), y
supongam os que lim x p/ ( x ) = r < + 00.
X->+oo
Luego, se tiene:
a) Si p > 1, entonces Ja+°°/(x)dx converge.
b) Si r 0 y 0 < p < 1, entonces f(x )d x diverge.
C o ro la rio 2. Sea / una función integrable en [a; t ] , V t 6 [a; b), (b e l ) y
supongam os que lim (b - x ) p/ ( x ) = r < + 00.
x-*b
Luego, se tiene
a) Si 0 < p < 1, entonces I / (x )d x converge.
Ja
b) Si r o y p > 1, entonces I / (x )d x diverge.
Ja
TÓPICOS DE CÁLCULO - VOLUMEN II
r ” d *
E je m p lo 15. Analice si ----- ----- converge o diverge.
h x 3V 4 x 5 + x 3 — 1
Solución
Considerando que
lim x 11/2-----, .....--.......— ■= — (en este caso p = — >
X - . + 0 0 x 3 V 4 x 5 4 - x 3 — 1 2 2 /
r +0° dx
se concluye, p or el corolario 1, que la integral I -----converge.
J2 x 3V 4 x 5 + x 3 — 1
f 5 dx
E je m p lo 16. Verifique si I — 2---------- ,2 converge o diverge.
^2 ^ )
Solución
1 1
Teniendo en cuenta que lim (x — 2 )3/2 ■------- - ------- ttttt = — 7= (en este
M J (x - 2 )3/2(x + 1 )3/2 3 ^3
caso p - 3/2 > 1), la integral es divergente (se usa el corolario análogo al
corolario 2, reemplazando (í> - x )p por (x - a )p).
f°
lice si I
J—oo
x dx
Ejemplo 17. Analice si j p = = = = = = ^ = converge o diverge.
V 2 x 9 4- 8 x — 10
Solución
x 1
La integral converge, pues lim x • ,-------- - (b = 2 > 1).
*-*+ “ V 2 x 9 + 8 x - 10 V 2
164www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-171-320.jpg)


![(F' APLICACIONES DE 'tts
LA INTEGRAL DEFINIDA
Hn este capítulo abordaremos algunas aplicaciones de la integral definida a ios
problemas geométricos, físicos y económicos.
4.1Á R E A D E R E G I O N E S P L A N A S
C A S O I: Sea /: [a;b] -» IR una función continua y f ( x ) > 0, V x 6 /. De la
interpretación geométrica de la integral definida se sigue que el área de la región
R limitada por la gráfica de /, el eje x, las rectas x = a y x = b (Fig. 4.1) está
dada por
A(R) = f ( x ) d x ^ u 2
C A S O II: Sean / y g dos funciones continuas en [ab] y g ( x ) < f ( x ) ,
V x £ [a; b]. E l área de la región íl limitada por las rectas x = a A x = b y
las gráficas de / y g (Fig. 4.2) está dada por:
A (n ) = ( í [f(x ) - g ( x ) ] d x ) u 2
Para demostrar esta fórmula, considerem os el número real k tal que k < g(x),
V x £ [a; b].
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-174-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
Efectuando una traslación de ejes al origen 0 '( 0; fc), las nuevas ecuaciones de las
curvas y = f(_x), y = g (x ) y de las rectas x = a y x = b son,
respectivamente, y x = f ( x ) —k , y x —g (x ) - k , x = a y x - b (por las
fórm ulas de traslación y x —y —k A xx —x). Por lo tanto, en el nuevo sistema
cartesiano x 10 ' y 1 se verifica
0 < g (x ) —k < f ( x ) - k , V x e [a; b]
Luego, teniendo en cuenta la fórm ula del caso I, se tiene
Observación 1. Si la región R está limitada por las gráficas de x = / (y ),
x = g (y), las rectas y — a A y — b (Fig. 4.3), donde f y g son funciones
continuas en [a; b] y g ( y ) < / (y ), V y E [a; b], entonces el área de la región R
es
a
y - o
Fig. 4.3
Fig. 4.4
E je m plo 1. Calcule el área de la región limitada por
71
y = sen x , x - 0 , x • y ~ ®
So lu ción
De la definición dada en el caso 1 y de la figura 4.4, se obtiene
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-175-320.jpg)
![APLICACIONES DE LA INTEGRAL DEFINIDA
I ¡implo 2. Calcule el área de la región S limitada por
2|x|
y , el eje x y las rectas x = — 2 y x = 1
1 + x 2
Solución
l'itr la definición de valor absoluto, se tiene que
r - x , x < 0
U , . x > 0
A m , por la fórm ula dada en el caso I y la figura 4.5, resulta
-1 2|x| ,
1*1 = {;
x r o = [ j
f° 2x f 1 2x
= - ------- r dx + ------- Tdx
J-2 1 + x J0 l + x 2
= - [ l n ( x 2 + 1 )]° 2 + [ln (x 2 + 1)]q = ln 5 + ln 2 = (ln 1 0 ) u 2
r.jemplo 3. Calcule el área de la región limitada por la parábola y = x 2 + 4x, el
eje x y las rectas x = - 2 A x = 2.
Solución
( »bservando la gráfica de la región (Fig. 4.6), se tiene que para / ( x ) = x 2 + 4 x se
m inple
/ ( x ) < 0, V x 6 [ - 2 ; 0] y / ( x ) > 0, V x 6 [0; 2]
l’or tanto, el área de la región pedida se descompone en la sum a de las áreasdelas
regiones y R2, es decir,
A ( R ) = A ( R 1) + A ( R 2)
f0 f 2 16 32
= - l ( x 2 + 4 x ) d x + I ( x 2 + 4 x ) d x = — + — •= 16 u 2
J-2 J0 J 3
169www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-176-320.jpg)
![Ejem plo 4. Halle el área de la región F limitada por las gráficas de
y - x 2 , y — x 3 , x - - 1 , x = 2
Solución
lin la gráfica de la región F (Fig. 4.7), se observa que
x 3 < x 2 , V x 6 [ - 1 ; 1] y x 2 < x 3 , V x e [1; 2]
Luego,
r 1 r 2 , 8 17 2 5 _
A(F) = J ( x 2 - x )d x + J( x 3 - x 2)dx = — + — = — u
I»
TÓPICOS DE CÁLCULO - VOLUMEN II
Ejem plo 5. H alle el área de la región limitada por las gráficas de
y = arcse n x , y = arccos x , y = 0
Solución
Las gráficas de las funciones y = arcsen x y y = arccos x están dadas en la Fig.
4.8. Ahora bien, por la definición de las inversas de estas funciones, resulta
x = sen y < x = eos y ,V y 6 [ü; - ]
Por consiguiente, el área de la región pedida es
,-71/4
,4 (12) = I (e o s y - sen y ) d y = ( V 2 - l ) u 2
Jo
liste ejemplo se puede resolver usando a x com o variable independiente, esto es,
/•>/2/2 r 1
/l(/2) = I arcsen x dx + f a rc c o s x d x
Jo J/2/2
lis evidente que en este caso el procedimiento es m ás com plicado que el anterior,
por lo que recom endam os al lector escoger adecuadamente la variable
independiente antes de aplicar la fórm ula del área.
170
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-177-320.jpg)
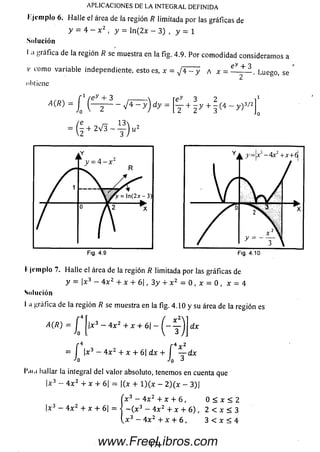

![E jem plo 9. H alla el área de la región F, ubicada en el primer cuadrante y que está
limitada por las gráficas de y = x 2 , x 2 = 4y , x + y = 6.
Solución
La región F se muestra en la Fig. 4.12. Los puntos de intersección de las curvas
en el primer cuadrante se hallan resolviendo simultáneamente los pares de
ecuaciones:
y = x 2
y
APLICACIONES DE LA INTEGRAL DEFINIDA
_ 6 _ x <=> x = 6 - x<=>x2 + x - 6 = Q=*x = 2 (para el prim er cuadrante)
y = x 2/4
y = 6 — x
.uego, el área de la región F es
y = 6 - x <=> — - 6 - x x - 241 - 2 (para el prim er cuadrante)
A(F) - A(Fi) + A(F2) = J ( x 2 - ^ x 2^Jdx + j ^ 6 - x - ^ j d x
1 1
= 2 + - ( 2 8 V 7 - 6 8 ) = - ( 2 8 a/7 - 6 2 ) u 2
Kjem plo 10. L a región F, limitada por la curva y = 1 0 * - 5 x 2 y el eje x, es
dividida en dos partes iguales por una recta que pasa por el origen. Halle la
ecuación de dicha recta.
Solución
La región F se muestra en la Fig. 4.13.
La pendiente de la recta L que pasa por
el origen y por el punto (a; 1 0 a -
.r>a2) es
1 0a — 5 a 2
m = --------------- = 10 - 5a.
a
Así, la ecuación de la recta L es
y = (1 0 - 5 a)x .
I’or otro lado, el área de la región F es
20
Fig. 4.13
/K F ) = I ( 1 0 * — 5x 2)dx —-—u2
Jo 3
A(F) 10
Ahora, com o F = F1 U F2,conA(F1) = A(F2), y A(Ft ) - —— = — , entonces
r a 5 10
M F i) = I [(1 0 x - 5 x 2) - (1 0 - 5 a)x]dx = - a 3 = — = > a = V 4
JQ 6 3
l’or lo tanto, la ecuación de la recta L es y = (1 0 - 5 Í4)x.
173www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-180-320.jpg)
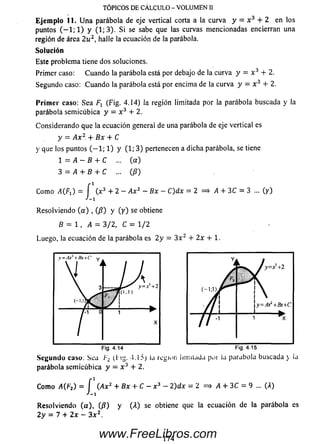
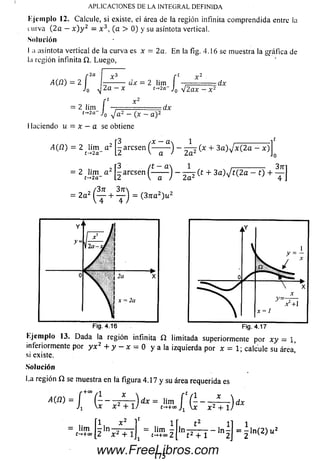

![17. í í es la región de m ayor área encerrada por las gráficas de S x2 - 4 y = 0 y
la elipse cuyos focos son los puntos (0, ± 6 ) y cuya longitud de su eje menor
es R- V5 n — 9V 5 arcsen — —
V V3 2 J
18. y 2 ~ x = 0 , y - x 3 = 0 , x + y - 2 = 0.
( 4 x - x z ( x 2 + 8 x — 40
l 9 - y = 4 ' . y = --------- 16--------• * > - ‘ . R .1 7 u >
x < 0 - 3 x - 1 6 , x < - 4
20. y ( x 2 + 4 ) = 4 (2 - x) , y = 0 , x = 0. /?, ^ _ l n 4 j u 2
2 1 . y = x 3 + x - 4 , y = x, y = 8 - x .
22. y — e x , y - e~x , x = 1. r ^e ~ ^
APLICACIONES DE LA INTEGRAL DEFINIDA
e
4
u 2
23. y — 2x + 2 , x = y 2 + l , x = 0 , y = 0 , x = 2. R. ( i s + í v ^
24. y = x ~ 2 , y + x 2 = 0 , x = 1 , x = 3. R — u 2
' 6
25. y = y/'x2 - 3 , y = x - 1|, y = 0. ^ ] n 3 - i ) u 2
26. y = |sen x| con x e [0; 2tt] , y + x = 0 , x - 2n = 0. R. (4 + 2 n 2) u 2
x 2 - 4
27- y = ^ T _ 16 > x = - 3 ' X = 3 . y = 0.
28. y = arcsen x , y = arccos x , x = 0. R. ( 2 - y j l ) u2
29. y = arcsen x , y = a r c c o s x , y = 0. r_ (y¡2 - i ) u 2
30. y = x 3 + 3 x 2 + 2 , y = x 3 + 6x 2 - 25. r . 10 8 u 2
31. y = x 2 , y = 8 — x 2 , y = 4x + 12. R. 6 4 u 2
32. y = x 2 , 2 y = x 2 , y = 2x. K. 4 u 2
<3. y + * = o , y = [ / ( t ) d t , d on d e / ( í ) = í 3 f2 1 f < 2 .
Jo l — 2 t — 1 , t.> 2
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-184-320.jpg)

![APLICACIONES DE LA INTEGRAL DEFINIDA
T>5. y =
X2
r, x 0, x — 1, y — 0. R,
(4 —x 2)3/2’ ' X ~ L> y ~ u- t y f '
56. y = 60(xs - x 4 + x 3),y = - 2 x , x 2 = 1. R. 52u 2
.r)7. y = x + sen x, y = x,x = 0, x = - . R —~ ^
6 ’ 2
58. 8 x = 2 y 3 + y 2 - 2y, 8 x = y 3, y 2 + y - 2 = 0. R.— u 2
u 2
59. x + y - y 3 = 0 , x - y + y 2 = 0. R. — u 2
96
37
12
2
,2
,2
60. y - c se n ( - ) ln ( s e n , x = 0 , x = a n . R. 2ac(l - ln 2 ) u
61. y 3 ( x - 2 ) 2 = 1 , y = 0 , x = 1 , x = 10. R. 9 u
62. y ( x 2 + 4) = 8 , 3 x 2 - 4 y - 8 = 0. R. 2(7r + 2 )u
63. Í2 es un arco de la cic lo id e cu ya ecuación param étrica es
x ci(t se n t), y = íz(1 — e o s £). R. 3 tccl2
f 2n
Sugerencia: 4(.fi) = y dx.
64. D. es la re gión lim itada p o r el astroide x = a e o s 3t , y = a s e n 3 t.
3
/? . - 7 T U 2
8
65. D. es la figura com p re n d id a entre la hipérbola x 2 - y 2 = 9 , el eje x y el
diám etro de la hip é rb ola que pasa por (5; 4). R. 9 l n 3
2 x
66. fí es la re gió n lim itad a p o r la gráfica de / ( x ) = -------- - , el eje x y las dos
1 -f* X
rectas verticales correspondientes a las a b scisa s de los pun to s m á x im o s
absolutos. A (]n 4)u 2
67. í í es la re gión lim itada por la gráfica de / ( x ) = 2 x 4 - x 2 , el eje x y las dos
rectas verticales que pasan p o r los puntos m ín im o s relativos.
R. (7 / 1 2 0 ) u 2
60. es la re gión encerrada p o r y 2 = x 2 - x 4. R. (4 / 3 ) u 2
69. Cí está lim itada p o r un lazo de la cu rva a 2y 4 = x 4 ( a 2 - x 2).
n 4íj2 ?
R. — u2
5
179
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-186-320.jpg)

![4.2 V O L U M E N D E U N S Ó L I D O E N F U N C IÓ N D E L A S Á R E A S D E L A S
S E C C I O N E S T R A N S V E R S A L E S
Sea S un sólido limitado en el espacio. Bajo ciertas condiciones es posible hallar
el volum en de este sólido. P or ejemplo, sea Sx una sección plana del sólido S
obtenido al cortar el sólido con un plano perpendicular al eje x en el punto de
abscisa x (Fig. 4.18) y supongam os que existe un intervalo [a; b] tal que
APLICACIONES DE LA INTEGRAL DEFINIDA
- u
xe[a:b]
Si >5(5X) es la función área de la sección plana (llam ada sección transversal de S)
y es continua, V x e [a; b], entonces el voium en del sólido 5 está dado por
í A(Sx)dx
Jn
Fig. 4.18 Fig. 4.19
Ejem plo 14. L a base de un sólido es la región limitada por la elipse
b 2x 2 + a 2y 2 - a 2b 2 .
I lalle el volum en del sólido S si las secciones transversales perpendiculares al eje
x son:
¡i) Triángulos rectángulos isósceles, cada uno con hipotenusa sobre el plano xy.
b)Cuadrados. c) Triángulos de altura 2.
Solución
a) La gráfica de la sección transversal del sólido se muestra en la Fig. 4.19. E l
sólido es la unión de los Sx, x 6 [— a; a], donde Sx es un triángulo rectángulo
isósceles de área
MSX) ~ b h = ^ ( 2 y)h = ( 2 y ) y = y 2 = ^ ( a 2 - x 2)
Luego,
f a b2 /4
F=J —(a2 - x 2)dx - i^-ab2J u 3
18!
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-188-320.jpg)
![h) Si las secciones transversales son cuadrados (Fig. 4.20), el sólido queda
descrito com o la unión de los Sx, x E [ - a ; a], tal que Sx es un cuadrado e
lado 2y = — y¡a2 - x 2 . Luego, el área de la sección Sx es
¿ ( S * ) = ( 2y ) 2 = 4 y 2 = 4 ^ ( a 2 - x 2)
TÓPICOS DE CÁLCULO - VOLUMEN II
= í 4 ^ j ( a z - x z)dx = ( ^ - a b ^ u 3
J~-n &
Por tanto, el volum en del sóiido es
b 2
y
J~a
c) S i las secciones transversales son triángulos de altura 2 (Fig. 4.21), ei solido es
la unión de los S*, x 6 [ - a ; a], tal que S * es el triángulo de altura 2 y base
2 y = — J a 2 - x 2 . Así, el área d éla sección plana es
a
1 2b r— —
A(.Sx) = - ( 2 y ) 2 = 2 y = — J a 2 - .
Por tanto, el volum en del sólido resulta
/-fl U _______ _
V = — y/a2 - x 2 dx = (n a b )u 3
L a a
l'ic m n lo 15 U na recta se mueve paralelamente al plano y z cortando a las dos
elipses b 2x 2 + a 2y 2 = a 2b 2 A c 2x 2 + a 2z 2 - a 2c 2, que se encuentran en los
planos x y y x z respectivamente. Calcule el volum en del cuerpo asi engendrado.
Solución
Kn este sólido, la sección Sx es un rom bo (Fig. 4.22) cuyas diagonales son
2 y A 2z. Luego, el área de la sección plana es
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-189-320.jpg)


![APLICACIONES DE LA INTEGRAL DEFINIDA
4.3 VOLUM EN DE UN SÓ LID O DE REV O LU C IÓ N
plana'urededor^e u n a íe c í fí^ c l)™ id a n ne r lt 7 d bT 'd0 ^ ^
llama eje de revolución. P 6 la regloa La recta fiJa se
4.3.1 M E T O D O D E L D I S C O C I R C U L A R Y D E L A N I L L O C I R C U L A R
: * , " < £ 4 M t 'o t o i i a d T T r a y - X = * ' (F ig - 4 2 n U secció" tra sv e rsa l
•'! q « p a l l l r e 'r T / “ “5" del SÓW0 5 P'“ o Perpendicular
• i ^ r , Por x e es un círculo de radio ivi = If f r 'U m « *
circular). El area de esta sección es 1/ M I (disco
A (sx) = n y 2 = n [ f ( x y2 i x e[a;b]
I -ucgo, por el método de las secciones transversales, el volum en de 5 es
Observación 2. Sea S el sólido de
't'volucion obtenido por ¡a rotación en
h>rno al eje y de la región plana R limitada
,a cu n a x = 9 (y) (g continua en el
intervalo [c ;d ]), el eje y y ¡as rectas
v - c A y - d (Fig. 4.25).
/ monees el volumen del sólido es
n fc [g(y)l2 d y ' j u 3
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-192-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
Observación 3. Sean f ,g[a-,b] R funciones continuas cuyas gráficas se
encuentran a un mismo lado del eje x, y además g(x) < ]/ (x )| , V x 6 [a; ó].
Sea S el sólido de revolución que se obtiene por la rotación en torno al eje x de la
región ü acotada por las curvas y = f(x) , y = g ( x) y ¡as rectas verticales
x —a , x = b (en la fig. 4.26, solamente se muestra el caso 0 < g{ x) < / (x )).
Como la sección transversal Sx obtenida por la intersección de S con un plano
perpendicular al eje x que pasa por x G [a; b] es un anillo circular (Fig. 4.27),
entonces el área del anillo circular es
¿ ( S * ) = Tt{[f(x)]2 - [g(x)]2} , x G [a; b]
Luego, el volumen del sólido de revolución S resulta
[g(x)¡2] d x u
revolución es
- a v - r ¿)dx u
donde R es el radio m ayor del anillo circular y r es el radio m enor (fig. 4.26), Si
r = 0 , la fórm ula es la que se obtiene por el método del disco circular.
Observación 4. Sean f ,g: [a;b] -> E funciones continuas cuyas gráficas se
encuentran en un mismo lado de la recta y = c y g(x) —c| < f(x) —c,
V x G |a; b]. Sea S el sólido de revolución que se obtiene al hacer rotar en torno
a la recta y = c la región Q 1imitada por ¡as gráficas de y = f (x), y —g{x),
x a y x = b (Fig. 4.28).
/■'.monees el volumen del sólido S es
V -• J ( l / 'M - c]2 - [g (x ) - c]2} d x j u 3
186
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-193-320.jpg)
![APLICACIONES DE LA INTEGRAL DEFINIDA
Observación 5. Si la región Q limitada por las gráficas de x = / (y ), x = g ( y )
r las rectas horizontales y = c , y = d gira alrededor de la recta vertical
x - k (Fig. 4.29), donde las gráficas de f, g están a un mismo lado del eje de
rotación y g(y) - k < |/(y) - k , V y 6 [c;d]. Entonces el volumen del
sólido de revolución obtenido es
v = (rc /cV ( y ) - k ]2 - [g(y) - k ^ d y ^ j u 3
Ejem plo 16. Calcule el volum en del sólido generado por la rotación alrededor
del eje x de la región limitada por las gráficas de y = e x, x = 0, x = 1, y = 0 .
Solución
l-a región se muestra en la figura 4.30. Aplicando el método del disco (R - e x), ■
se obtiene
V = n f (ex) 2 dx = n í e 2x dx = ^ ( e 2 - 1) u 3
Jo Jo 2
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-194-320.jpg)
![TÓPICOS DE CALCULO - VOLUMEN II
Ejem plo 17. La región limitada por las gráficas de y — a re se n x , y — 0 y
x ~ —1 gira alrededor del eje y. Calcule el volum en del sólido engendrado.
Solución
C om o el eje de rotación es el eje y, consideramos a y com o variable
independiente. L a región se muestra en la Fig. 4.31.
C om o R = 1 y r = - sen y, entonces el volum en del sólido es
Ejem plo 18. L a región limitada por las gráficas de y - x 2, y - V * y x - 2
gira alrededor del eje x. Calcule el volum en del sólido.
Las curvas y = x 2 y y = V * se cortan en los puntos (0; 0 ) y (1; 1). En la
Fig. 4.32 se muestra la región entre ellas y la recta x = 2. E n la primera región,
(0 < x < 1) una sección transversal es un anillo circular con radio m enor r = x
y radio m ayor R — V * . E n la segunda región (1 < x < 2), la sección transversal
es un anillo circular con radio menor r = yfx y radio m ayor R = x 2.
Por lo tanto, el volum en del sólido S es
ry 1 1° n 2
= ir - + - s e n ( 2y ) = — - u 3
2 4 J-E 4
2
1 1
+ - s e n ( 2y )j
Solución
V = n - ( x2) 2]dx + n ¡ ( x 2) 2 - ( ^ f ) d x
3
X
x = 3
Fig. 4.32 Fig. 4.33
1 8 8
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-195-320.jpg)
![Ejemplo 19. L a región limitada por la circunferencia (x + 2 ) 2 + ( y >- 2 ) 2 = ]
j'.iiii aliededor de la recta x — 3. Calcule el volum en del sólido generado (toro de
revolución).
Solución
I .a región se muestra en la fig. 4.33, donde
/ ( y ) = - 2 - V i - (y - 2 ) 2 A g ( y ) = - 2 + / i - (y - 2)T
Así, el radio m ayor /? y el radio menor r son, respectivamente,
= 3 - / ( y ) = 5 + V i - (y - 2) 2 y r = 3 - 5 (y ) = 5 - v' l - ( y - 2)2
Luego, el volum en del sólido de revolución es
V = 7i (R2 - r 2) d y = n 2 0 ^ Y ^ ( y ^ 2 y d y
= ÍOn [(y - 2) V i - (y - 2 ) 2 + a rc se n (y - 2 )] = ( 1 0 n:2) u 3
Ejemplo 20. La región limitada porla elipse b 2x 2 + a 2y 2 = a 2b z con
0 < b < a gira alrededorde su eje mayor. Calcule el volum endel sólido
generado.
Solución
C om o la elipse es simétrica respecto al
eje mayor, podem os considerar que el
sólido es generado por la rotación de
la región som breada en la fig. 4.34
alrededor de! eje x. A sí, el radio de
giro del disco circular es
b i------------
R = y = - V a 2 - x 2
a
Por consiguiente, el volum en del
sólido de revolución es
í a í a b 2 /4
V = n j R2d x = n J — ( a 2 - x z)dx = y - a b 2n j u 3
Ejemplo 21. L a región infinita comprendida entre la curva x + x y 2 - y = 0 y
su asíntota vertical gira alrededor de su asíntota vertical. Calcule, si existe, el
volum en del sólido.
Solución
Al despejar x de la ecuación, obtenem os x = „ V , con lo cual la asíntota
1 + y 2
vertical de esta curva es x = 0 (eje y), pues y -> ±00 <=> x -> 0 .
APLICACIONES DE LA INTEGRAL DEFINIDA
189www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-196-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
Considerando que la curva (Fig. 4.35) es simétrica con respecto al origen y el radio
de giro en el p rim er cuadrante es R = x = ^ -j . entonces el volum en del sólido
es
V = 2tc í R2d y = 2n í
J o J o (i+ y 2) 2
Haciendo y = tan 9, la integral resulta
y = 2K, ! iS . [ íarctan(>,)- 2 ( i + 7 ) ] 0
= 2” tÜ !S ,[iarctan(t)- 2 c T T F ) ]
+ oo 2 f t y 2
d y = 2n Jim _ „ , d y
/ní-+oo J0 ( i + y 2Y
Eje m plo 22. Determine el volum en del sólido de revolución generado al rotar
alrededor del eje x la región infinita com prendida entre la recta y = O y la curva
y = L
Solución
1.a resiión se muestra en la Fig. 4.36. A l aplicar el método del disco, se obtiene
r + “ / i 2 r +" _ !
i' H 1 t e ) ; t 3 ‘b
= , M im j V « «fe = ’', l i ? „ l - 3 * ' ‘/3 l'l = * tü 5 . ( - í r o + 3 )
= 37T u 3
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-197-320.jpg)
![Sea f [a;b] -» K , a > 0 una función continua y no negativa y S el sólido dé
revolución obtenido al hacer rotar en torno al eje y la región í í limitada por las
f raileas y = / ( * ) , y = 0, x = a A x = b (Fig. 4.38)
APLICACIONES DE LA INTEGRAL.DEFINIDA
4.3.2 M ÉTO D O DE LA C O R TE Z A C ILIN D R IC A
i:i sólido S (Fig. 4.39) puede ser considerado com o la unión de los cilindros C
x G [a; b], es decir, * ’
5 = U Cx
x e[a :b ]
C om o el área (lateral) de cada cilindro circular recto Cx está dado por
A(CX) = 2nx f ( x ) ; x 6 [a,b]
se deduce que el volum en del sólido S es
K = í A(Cx)d x - 2n f x f ( x ) d x
Ja
Observación 6. Sean f ,g: [a; b] -> M
funciones continuas en [a;b] tales que
,<l(x) < / ( * ) , V x e [a; b], y S el sólido de
revolución obtenido al hacer rotar alrededor
de la recta x - c , con c < a, la región Q
limitada por las curvas y = f ( x ) , y = g(x)
r las rectas x = a y x = b (Fig. 4.40).
l-.ntonces el volumen del sólido S es
V = Í2 n (x - c) [ f(x) - g ( x ) ] d x u
Fig. 4.40
191www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-198-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN 11
Observación 7. Sean f ,g [a; b] •-> E
funciones continuas en [a; b] tales que
g ( x ) < f [ x ) , V x e [a,b], y S el sólido de
revolución obtenido al hacer girar alrededor
de la recta x = c, con c > b, la región Q
limitada por las gráficas de x = a , x = b ,
y = f(x) , y = g ( x ) (Fig. 4.41). El volumen
del sólido S es
K = ( 27t J (c - x) [ f ( x ) - g(x)]dx"ju3
Fig. 4.41
Observación 8. Sea Q la región limitada
por las gráficas x = f ( y ), X = g(y),
y = a A y = b (Fig. 4.42), donde f y g son
continuas en fa; b] tales que g ( y ) < / (y ),
V y G [a,b], y S el sólido de revolución que
se obtiene a! hacer rotar la región Q
alrededor de la recta y = c, con c < a . El
volumen de S es
V = (^2n j (y - c)[/(y) - s(y)]d yj u3
Observación 9. Sea Q la región limitada por
las gráficas de x = g (y), x = f ( y ), y = a
A y — b (Fig. 4.43), donde f y g son
continuas en [a; fa] tales que g { y ) < / (y ),
V y 6 [a; b], y S el sólido de revolución que
se obtiene al hacer rotar la región Q
alrededor de la recta y = c, con b < c. El
volumen del sólido S es
V = ^2n J ( c - y ) [ f ( y ) - g ( y ) ] d y j u 3
Fig. 4.43
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-199-320.jpg)
![l'.jemplo 23. Encuentre el volum en del sólido engendrado al girar sobre el cíe y
l:i región limitada por la curva y = (x - 2 ) el eje x y la recta x = 3 .
Solución
1.a región se muestra en la figura 4.44. Aplicando el método de la corteza
leñemos
V = ZU i X ^ dx = ¿Tl2 x (x ~ 2 ^ dx
= 2n í (x4 - 6x3 + 12x2 - 8x)dx
h
147r
=
A P L IC A C IO N E S D E L A IN T E G R A L D E F IN ID A
l'.jemplo 24. Halle el volum en del sólido generado por la rotación de la región
limitada por las gráficas de x + y2 + 3 y - 6 = 0 , x + y - 3 = 0 alrededor de
la recta y = 3.
Solución
l a región se muestra en la figura 4.45. C om o el eje de revolución es horizontal, el
volum en del sólido es
V = 2n f (3 - y ) l (6 - 3 y - y 2) - (3 - y ) ] d y
J - 3
= 2n f ( y 3 - y 2 - 9 y + 9) d y
J_3
256tt ,
= — ^— Uá
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-200-320.jpg)
![TOPICOS DE CÁLCULO - VOLUMEN II
Ejem plo 25. Calcule el volum en del sólido de revolución que se obtiene al girar
alrededor de la recta x = 1 la región limitada por las gráficas de
y — ¡x2 — 2x — 3 , y + l = 0 , x — 1 = 0 , x —4 = 0
Solución
La región se muestra en la figura 4.46. A l aplicar el método de la corteza
cilindrica, el volum en del sólido es
V = 2n J (x - l) [ | x 2 - 2x - 3| + 1]dx
Usando la figura 4.46 y la definición de valor absoluto, se tiene
¡xz - 2x - 3| = | 0 - 3 ) 0 + 1)1 = { _ ( * 2 ~ 2X ~ 3) ' 1 ~ x < 3
De aquí resulta
V
2 x - 3 , 3 < x < 4
= 27r|j O _ 1)[(3 + 2x - x 2) + l]dx + J (x - 1) [ 0 Z _ 2x - 3) + 1] dx
= 2n ( - 4 + 2x + 3x2 - x 3) dx + J O 3 - 3 x 2 + 2)dx
( 3 5 ^ 59 ,= 2^ ( 6 + T ) = y 7 r u 3
Ejem plo 26. Calcule el volum en del sólido que se obtiene al rotar alrededor de
la recta y = 3 la región Í1 = { O ; y ) e M 2 / O < x < c o sh - 10 ) - O < y < 2}.
Solución
La región £2 se muestra en la Fig. 4.47. Esta región está limitada por x = c o sh y ,
x - O, y O A y = 2. C om o el eje de giro es la recta horizontal y — 3,
entonces el volum en del sólido de revolución es
V = 2n í (3 - y )(c o s h y ) d y = 27r[senh(2) -!- c o sh (2 ) - l ] u 3
Jo
1 9 4
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-201-320.jpg)
![Ejem plo 27. L a región infinita comprendida entre la gráfica de x y 2 = ( 3 a —x )
(<i > 0) y su asíntota vertical x = 0 gira alrededor del eje y. Calcule el volum en
del sólido generado.
Solución
Con la ayuda de la región que se muestra en la figura 4.48, el volum en del sólido
pedido es
A P L IC A C IO N E S DE LA IN T EG R A L D E F IN ID A
9a2n 2
— ^— u
Fig. 4.48
E JE R C IC IO S
Ivn los siguientes ejercicios, calcule el volum en del sólido generado por la
rotación de la región Q alrededor de la recta L, donde
1. L ■ eje x ; 12 : y = x 2 , y = 4x. (*)
(*) Entiéndase Q lim itado por las gráficas de y = x 2 Ay = 4x.
, 3 17T ,
2. L: y — 0 ; I] ■■y = (x — 1) 3 , x = —1,x —0 , y — 0. R. — - u 3
160
3. L ■ y = 0 ; SI : x 3 - 5 x 2 + 8x — 4 , y = 0. R. - ™ u '
195www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-202-320.jpg)


![TÓPICOS DE CÁLCULO - VOLUMEN II
45. L y = 2 ; íl-.y = l n x , y = 0, x = 0, y = 2
46. L:x = e 3 ; i2 :y = ln x , y = 0 , x = 0 , y = 2
1 28
~3
40
~3
47. L:x = - 2 ; íl: y = 0, y = 4 - x 2 R . ^ - t c u 3
r- 40 *
48. L-.y = 2 ; Í2 :y = 0, x = 4, y = Vx R. — n u 3
1 ( 1 4 5 ,
4 9 . L : y = - 2 ; ¿2:y = V x - -^=, x = 1, X = 4, y = 0 K. 7r ( h i 4 + — J u ó
n
SQ. L: y = — 2 ; /2:x = y sen y, x = 0, y = g
C O S % 7T 7T
51. L: eje x ; ¿2:y = ' ^ sen' ¿ - y = 0, x = a, x = - con 0 < a < -
7T y - cos a + ln ( V 2 - 1) - ln (c sc a - ept a ) u 3
52. L: y = 0; ¿2:y = (x + l) e * , x = 0 , x = l,y = 0
53. L : x = 0; /2:y = e x y = 0, x = 0, x = 1 R. 7r(e - l ) u 3
54- Lx = 7) ü : y = x e 2*, x = l , x = 3, y = 0
55. L : y = - 1 ; J3:y = ln x , y = 0, x = e R. 7ieu3
56. L: eje x ; Í2: x 2y 2 + 1 6 y 2 = 16, x = 0, y = 0, x = 4 R. n z u 3
/a V 3
57. ¿ : e j e x ; /2: T riá n g u lo equilátero con vértices (0; 0), (a ; 0), I - ; — a
n a 3
*• —
58. L : x = - 3 ; /2: y = x 5 + 8 , y = ( x 3 - 2 ) 2, x = 0
59. l eje y ; /2: es la región cerrada por el lazo de la curva ( y 2 - b 2) 2 = a 3x
2 5 6 n b 9 _
R. ------.— r- u 3
3 1 5 a 6
60. L’. e j e x ; Í2 es la región encerrada por el lazo de la curva
= q x ( x - _ 3 a ) a > 0 R ™ (15 _ 16 ln 2 ) u 3
x - 4 a ¿
61. L: x = 4 ; Í2: x 2y 2 + 1 6 y 2 = 16, x = 0, y = 0, x = 4
R. 3 2 tt[1 - V 2 + ln ( 1 7 V 2 ) ] u 3
62. L : e j e x ; fl es la región, en el primer cuadrante, acotada por:
16 ,— o
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-205-320.jpg)
![__________ 2 3
(.3. L:e]ex; H: y = e~xJ c o s ( e ~x) , x = l n - , x = l n -
n n
R■ —[(3 - V 3 )n - 3 ]u 3
6 25
()4. L: x = 1 ; ú : x 2 - 4 = y, y = - 3 x fl. ------- t t u 3
6
(i.r>. eje y ; /2 es la región que se encuentra al lado derecho del eje y limitada
por x = 0 , (4 + x 2) y 2 = 4 - x 2 /?. 47r (7r - 2 ) ií3
(>6 . A la curva ^/xy - 2 x + 3 y - 6 = 0, en el punto (3; 3) se trazan las rectas
tangente y normal. Calcule el volum en del sólido generado por la rotación
alrededor de la recta y = - 3 , de la región limitada por la tangente, la normal
10222
norm al trazada y el eje y. R. ----------n u3
49
(i7. A la parábola y 2 = 12x, en el punto de abscisa 6 , se ha trazado una
tangente. Calcule el volum en del sólido generado al girar alrededor del eje x,
la región limitada por la tangente trazada, el eje x y la parábola.
R. 72n u 3
(.8. L: eje x ; íl: y = x e x, y = 0, x = 1 ' R. - <e 2 - l ) u 3
4
69. L: eje x , ü: es la región limitada por y = 0 y un arco de la cicloide
x — a ( t sen t), y = a ( l - eos i) R. 5 n 2a 2u 3
70. L : e j e y ; fl es la región del problema 69 R. 6 n 3a 3u 3
KCL3
71. L:x = a n ; SI es la re gión del problem a 69 R. ------( 97r 2 - 1 6 )u 3
6
72. L .y = 2 a ; ü es la región del problema 69 R. 7 n 2a 3u 3
73. L: eje x ; fí es la región limitada por x = a e os3t , y = a se n 3t.
74. Sea /; [ 0 ; + 00) -» ffi una función continua tal q u e / (x ) > 0 , V x > 1. Para
todo a > 1, el volum en del sólido generado por la rotación de la región
limitada por las gráficas de y = / (x ), x = 1 , x = a y el eje x, alrededor
/ -a
APLICACIONES DE LA INTEGRAL DEFINIDA
del eje x es: V = + 2 a 2 - - j u 3. Determ ine f(x).
R. f ( x ) = .V x 2 + 4 x
Vtt
75. Sea /: [0; + 00) -> K una función continua. Para todo a > 0, el volum en del
sólido generado por la rotación en torno al eje x de la región que se encuentra
entre la gráfica de y = / ( x ) y el eje x, desde x = 0 hasta x = a con a > 0
es V = ( a 2 + a ) u 3 . Determine / (x ).
199www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-206-320.jpg)

![APLICACIONES DE LA INTEGRAL DEFINIDA
i. i LO NG ITUD DE A RC O
Se;; / : [a; b] -» R una función con derivada continua en [a;b] y
P - {x0, x1 , una partición de [a;6], Esta partición define una poligonal
c o n flu id a por los segmentos rectilíneos desde ^ ( x , ^ ; / ( * , _ , ) ) hasta
< M * ¿ ; / ( * ¡ ) ) , p a r a i = 1,2, ... , n (Fig. 4.49).
n n
L{p) = = Z V O i - * ¡ - i ) 2 + (/ (.rj -
¿=1 i=1
i I numero ¿ - ¡|{i|m o L(P), si existe, se llama longitud de arco de la curva
y = f { x ) desde ei punto(a ;/(a)) hasta el punto (£>;/(£)). Dem ostrarem os
que eneste caso el número Lsiempre existe.
Com o f es derivable y continua en [xt_ i ; x t] , i = 1,2.....n, por el teorema de
Lagrange o del V a lo r M edio, 3 t ¡ 6 ( x ^ X t ) tal que
f (x¿) — = f (ti)(x ¡ — x ¡_ x) , i = 1,2,..., n
I laciendo A¿x = x¿ —x , i = 1,2,..., n , tenem os
■ A n
= V (A¡ * ) 2 + [ / '( t i)]2.(A 1x)2 = V V i + [ / '( t ¿)]2
Í=1 fet
l’or tanto, la longitud de arco de la curva y = / ( * ) desde x = a hasta x = b es
n
1 ~ I & I W M . es decir
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-208-320.jpg)
![TOPICOS DE CALCULO - VOLUMEN II
Observación 10. La longitud de la curva x = g ( y ) comprendida entre las rectas
y = c A y = d, donde g es unafunción con derivada continua en [c; d], es
1 = (j ■/1+ífj'(y)]-dyju = | J j l +
4
Observación 11. Si la ecuación de la curva C viene dada en forma paramétrica
mediante un par de funciones con derivadas continuas, esto es,
C:£ : $ r
Entonces la longitud de la curva C desde t = a hasta t = fi es
¿ = Vl*'(t)]2+ [y'(OP dt'Ju
E je m p lo 28. H alle la longitud de la curva
,-------------- (1 + Vsec2x + 1 n n
y = v sec2x + 1 - ln ---------------------- desde x = — hasta x = -
' secx J 4 3
So lu ción
A l aplicar las reglas de derivación y sim plificando se obtiene
^ = tan x V se c 2x + 1
dx
Por lo tanto, con la fórm ula de la longitud de arco resulta
L = f 1 + ® dx = f * [1 + tan2x (se c 2x + l )]1' 2 dx
4 / 4 4 K d x J J ” / 4
rn/3
= I sec2x dx = [tan x nJ^ = (V 3 - l ) u
E je m p lo 2 9 Encuentre la longitud de la curva cuya ecuación es
desde x = —2 hasta x = — 1 .
So lu ción
1 x4 d y x 3 1
Com o y = — r + — ,entonces — = —-Luego, la longitud de arco es
J 2x216 dx 4 x 3
l = £ 4 T 7 W ? = £ J ( £ + i ) ¡ i - + 1
- Í T ( ^ ¿ )
dx
(x 3 1 21
■+ — I dx = — u
202
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-209-320.jpg)
![APLICACIONES DE LA INTEGRAL DEFINIDA
Ejem plo 30. Calcule 4a longitud total de la curva cuya ecuación es:
n n
- < x < -
2 ~ 2
y - J ^ V c o s t d t , - ^ < x < ^
~2
Solución
C r 7T 7Ti
Como f ( x ) = J ^ V e o s t dt, V x 6 entonces f ' (x) = V c o s x es
~2
. r ^
continua en el intervalo - j . Por lo tanto,
2 5 ___________ re
L = J * V 1 + c o s x d x = dx = P e o s ( | ) d x = 4 u
~2 “ 2 “ 2
Ejem plo 31. H alle el perímetro del triángulo curvilíneo lim itado por el eje de las
abscisas y por las curvas cuyas ecuaciones son *
y = In ( c o s x ) , * e A y = l n ( s e n x ) , x 6 ( 0 ; n )
Solución
Las gráficas de f ( x ) = ln ( c o s x ) , x 6 y de g ( x ) = ln ( s e n x ) , x 6 (0;n)
se muestran enla figura 4.50. La s longitudes de los lados del triángulo curvilíneo
son
n
¿1 = 2 “
[ n / * _________________ r n ¡ 4
¿ 2 = 1 V 1 + [ / 'O O P d x = | V i + ta n 2x d x = ln ( V 2 + l ) u
h Jo
( n,z /------------------- ( n'2 /---------------
¿3 = j V 1 + [5 '( x ) ] 2 = V i + cot2x dx = ln ( V 2 + l ) u
•'/r/4 ^rr/4
Por tanto, el perím etro del triángulo curvilíneo es P = + 2 ln (V 2 + 1)] u
203www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-210-320.jpg)

![lin cada uno de los ejercicios siguientes, determinar la longitud del arco de la
curva descrita por
c , ,a + V a 2 - x 2 i---------- ra ai
/ ( x ) - a ln(----------------- ) - V a 2 - x 2 ,x e R. (a ln 3 )u
APLICACIONES DE LA INTEGRAL DEFINIDA
E JE R C IC IO S
/ ( * ) =
a:4 + 3
6x
* 6 [1 ; 3] R.
( y ) “
,i. / O ) = X1' 2 - - x 3/2, x £ [0 ; 1]
/ ( x ) = V e2* - 1 - arcsec(e*) - 1 , x -£ [0; 4]
f W =
6 2x
O.
7.
I).
9.
10,
11.
12.
13.
14.
x e [2; 5]
/ (x) = ln (-x ) , x e [-V 8 ; - V I ]
X X —— —
f (x ) = - a r c s e n x - - V l - x 2 , x e
4
R. - u
R. (e4 - 1)U
393
fi' lo-“
* . ( l + í !»§)<*■
*•
/ ( x ) = ¿ W * 2 - 1 - ^ ln ( x + V x 2 - 1) , X £ [3; 5] R. 8 u
x = i y5/3 ~ ^ y 1/3-y e [0;i]
y = (9 - x 2/3) 3/2, x £ [1; 2]
2 7
/?. — u
20
9 3/—
R. - ( V í - 1)u
y = - W 3 - x 2 + ^ a r c s e n ^ x j , x £ [0; 1] /?. +
y - 1 - ln (c o s x ) ,x £ ¡0 ;£ ] fí. In ( V 2 + 1) u
y = arcse n (e *), x £ [0 ; 1]
x
y = a c o s h - , x € [0 b]
a
y 2 i
x = T ~ 2 l n y , y e[1;e]
l(>. / ( x ) = ln ( c o t h - ) ,x £ [ a ; b ] , a > 0
R. ln(e + V e 2 - 1) u
/b>
R. a senh
( e 2 + 1
R.
R.
’ e 26 - 1
ln^ _ i ) + a ~ b
205www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-212-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
17. / ( * ) = y + ¿ . * e [ 1;2]
18. x = (a 2/3 - y 2/3)3^2 , y e [-a ; a]
59
R- 7T7U
2 0 . x =■e c sen t , y = eos t, t e [0 ; 7r] R. v 2 (e ’r - 1)u
R. 3 a u
R. — [ V 2 + l n ( l + V 2 )]u
R. V 2 ( e ’r - l ) u
punto m ás próxim o donde la tangente es vertical. R. ln — u
2 2 . x = a (eos t + t sen t) , y = a (se n t - t eos t ) , t e [0 ; a]
R. ~ a a 2u
II. E n los siguientes ejercicios, halle la longitud de arco de las curvas que se
indican.
1. L a longitud total de la circunferencia x 2 + y 2 = a 2 R. 2na u
2. L a longitud total del astroide x = a e os3t , y = a se n 3t R. 6 a u
3. L a longitud del arco de la rama derecha de la tractriz
7. La longitud de la curva 9 y 2 = 3 x 2 + x 3 desde x = - 3 hasta x - 0
desde y = a hasta y = b con 0 < b < a. R. a l n ^ - J u
/Xn2/3 /y>.2/3
4. La longitud de la curva ( - J + M = 1 en el p rim er cuadrante.
a 2 + ab + b 2
R. -------------:------ u
5. L a longitud total de la curva cuya ecuación es
4 ( x z + y 2) - a 2 = 3 a 4/3y 2/3 R. 6au
6 . L a longitud total de la curva 8y 2 = x 2 - x 4 R. W 2 u
R. 4V 3i¿
206
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-213-320.jpg)
![II l a longitud de arco de la parábola semicúbica 5 y 3 = x 2 com prendida dentro
134
de la circunferencia x 2 + y 2 = 6 R. — -u
27
•J. Calcule el perímetro de la región de menor área limitada porlas gráficas
y 2 = 2 x 3 A x 2 + y 2 = 20
X2
II). I,a longitud de la curva y = - - In V x ,desde x = 2 hasta x = 3 .
II. La longitud de la
uirva y = V x - x 2 + arcse n V x. R. 2 u
I L a longitud total de la curva dada por (y - arcsen x ) 2 = 1 - x 2 R. 8u
2
13. La longitud del arco de la curva y 2 = - ( x - l ) 3 com prendida dentro de la
x
parábola y — —
14. La longitud del arco de la curva dada por x = ( t 2 - 2 )se n t + 2 t eos t ,
71^
y = (2 - t2) eos t + 2t sen t, desde t = 0 hasta t = n
15. La longitud del arco de la curva y = ln ( l - x 2) desde x = 0 hasta x = 1/2
R. [ - ¿ + I n 3 ] u
III. L o s siguientes ejercicios tratan del m ovim ientode una partícula.
1. En el tiempo t, una partícula se encuentra en el punto
P (c o s t + t se n t ; sen t - t eos t)
Encuentre la distancia recorrida desde el instante t = 1 hasta t = n
2. En el instante t, la posición de una partícula es
x = 1 + arctan t ,y = 1 - ln / 1 + t 2
Halle el recorrido desde el instante t = 0 hasta t = 1 R. ln ( l + V 2 ) u
APLICACIONES D E L A INTEGRAL DEFINIDA
207www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-214-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
4.5 ÁREA DE UNA SU PER FIC IE DE R EV O LU C IÓ N
Sea /: [a, b] -> M una función no negativa, con derivada continua en [a; £>].
Haciendo girar la gráfica de / desde x = a hasta x = b , alrededor del eje x, se
obtiene una superficie de revolución (Fig. 4.52). E l área de esta superficie de
revolución está dado por
i4(S) = (271 f f(x)yj 1 + [ f ( x ) ] 2dx
Fig. 4.52
Observación 12, Si la curva se describe por la ecuación paramétrica
C :x = x(t), y = y (t), t e [a;/?]
donde x( t ) y y ( t ) son funciones con derivadas continuas en [a; /?J, entonces el
área de la superficie generada al hacer girar la curva C alrededor del eje x es
A(S) = ( l n J % ( t ) V [ * '( O P + ty'(t)]2dt
Observación 13. Sea f: [a, b] -> E unafunción con derivada continua en [a; b]
tal que su gráfica está a un mismo lado de la recta y = c . Haciendo girar la
gráfica de f desde x = a hasta x = b alrededor de la recta y - c se obtiene
una superficie de revolución (Fig. 4.53) cuya área es
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-215-320.jpg)
![.APLICACIONES DE’LA INTEGRAL DEFINIDA
Observación 14. Si la curva C se describe con la ecuación x = g (y ), V y 6
I": H donde g es unafunción con derivada continua en [a; b] y S e s la superficie
./<• revolución que se obtiene al hacer rotar la curva C alrededor de la recta
= c , (Fig. 4.54), entonces el área de la superficie S es
4(5) = i^2n J g(y) - c^jí + [ g '(y W d y ^ ju 2 (*)
Si la ecuación de la curva C está dada en su form a paramétrica por
x = x ( t y = y(t), Vt 6 [a; /?]
donde las funciones x = x(t), y = y ( t ) tienen derivadas continuas en [a;/?]
entonces la fórm ula ( * ) se transforma en
A(S) = Í 2 n ( |ar(t) - c|V"[x'(t)P + [y'(t)]2 d i) u2
Y
b
k C >
-----------------. c
/ n(y)
i
S
c
a - - J *x -
.Y C
.....w -----------►
x
.Y - C
Fig. 4.54
Ejem plo 34. H a lle el área de la superficie generada al hacer girar la gráfica de
/ (x) = V24 — 4x , x £ [3; 6], alrededor del eje x.
Solución
—2
(.orno f' (x) - — , el área de la superficie resultante es
V 2 4 - 4x
4
6
f ( x y i + [ f ( x ) ] 2dx
= 2 n V 2 4 - 4x 11 + — 4 dx
h y] 24 - 4x
= 2n I V 2 8 — 4x dx = ----- u2
h 3
l a gráfica de f ( x ) = /24 - 4x se muestra en la figura 4.55.
4 ( S ) = 2n f
Ja
209www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-216-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
Eje m plo 35. Halle ei área de la superf
del eje y del arco de la curva y = a eos
So lu ción
Considerando que la curva (Fig. 4.5«
superficie generada es
A(S) - 2tt f /(y)V 1 + [/'(y
•'o
/y dx
donde x = / ( y ) = a cosh y —
Luego.
A(S) = 2n J a cosh Jl-<
= 2n J a c o sh 2 d y
Eje m p lo 36. Halle el área de la super
2x = y v V - 1 + ln ¡y - J y 2 - l | ,
So lu ción
L a ecuación paramétrica de la curva e:
.* (0 = ^[t%/t2 - l + l n | t -
y ( t ) = t
de donde x' (t ) = V t 2 - 1 A y'(t)
Por tanto, el área de la superficie es
a (s ) = í y c o T I x ' M F n / M F í
h
YJ
c >
y
a: = a c o sh (— )
a
'" " A .
C7i
— y <
f > r0 a a cosh(l) x
Fig. 4.56
cié engendrada por la revolución airededor
- 'i desde x = a hasta x = a cosh ( 1)
a '
>) gira alrededor del eje y, el área de la
)]2dy
= f ' ( y ) = s e n h Q
- se n h 2(^ )d y
n a 2 , „ ,
= ------(2 + senh 2 )u
2
ície cuando la curva
y e [2 ; 5], gira alrededor del eje x.
^ f2 ~ 1 B , t 6 [2; 5]
= 1
!t = 2jt í t-J (t2 - 1) + 1 dt = 78n u2
210www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-217-320.jpg)
![APLICACIONES DE LAINTEGRAL DEFINIDA
I1'templo 37. Halle el área de la superficie generada por la revolución en torno al
r l r y del arco de la curva y = - [x2 - 21n x], x e [ l ; 4 ].
Solución
1.1ecuación paramétrica de la curva es
(x(t) = t
y ( 0 = ^ [ t 2 - 2 1 n t ] ’ 1e [1;4]
1 1
tic donde x'(t) - 1, y '(t) = - (t - -)
ucgo,
A(S) = 2?t J| x ( t y [ x ' ( t ) ] 2 + [y'(t)]2dt
= 2„ J , J l + i ( , - i) * d t = 2 , J ‘ l (, + | ) d t = 2 4 ™ ’
I jemplo 38. Calcule el área de la superficie de revolución que se obtiene al hacer
líirar la curva y = 2 - e x , desde x = 0 hasta x = 2 , alrededor de la recta
V - 2
Solución
I .i gráfica de la curva se muestra en la
ligura 4.57.
Se tiene que
dy
¿ = f ' M = - e x
luego, según la fórmula, el área de la
superficie es
¿(S ) = 27r f ( 2 - f M ) J l + [f'(x)]dx
*'0
= 2n í exyfí'+ (ex)2 dx
“'O
: 7r |e 2V l + e4 - V2 + + ln
e 2 + V i + e ‘
1 + V 2
211
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-218-320.jpg)
![Ejem plo 39. Halle el área del elipsoide de revolución que se obtiene al hacer
x 2 v 2
girar la elipse — + — = 1,alrededor de:
a) su eje m ayor b) su eje menor
Solución
a) Cuando la elipse gira alrededorde su eje mayor, es suficiente considerar la
curva C descrita p o r / ( x ) = --^ 2 5 - x 2, x e [— 5; 5] (Fig.4.58).
4 i----------- 4 x , , , ,
Al em plear / (x ) = - V 25 - x 2 A / '( x ) = - ^ = = = , el area de la
TÓPICOS DE C Á LC U LO -V O LU M EN II
superficie resulta
r 5 ¿J, __________
A(S) = 2n j - V 2 5 - X ' l f
1 6 x 2
25(25 - x 2)
dx
/ 100 3
= 27r ( l 6 + — arcsen -Jw
b) Cuando la elipse gira alrededor de su eje menor, es suficiente considerar la
curva x = - V l 6 - y 2, y 6 [-4 ; 4] (Fig.4.59).
4
Luego, el área del elipsoide generado es
5
A(S) = 2n J j V l 6 - y 2
/ 8071, ,
= Í507T + - ^ - l n 4 J u 2
1 +
2 5 y z
1 6 ( 1 6 - y 2)
dy
2 1 2
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-219-320.jpg)
![I. E n cada uno de los siguientes ejercicios, halle el área de la superficie de
revolución que se obtiene al girar alrededor del eje x, las curvas dadas por
1. / ( x ) — —x 3 , x £ [0 ; 2] /?. (9 8 tt/ 8 1 )u 2
2. / ( x ) = c o s x , x e [ - j ; | ] R. 2jt[V2 + l n ( l + V 2 )]u 2
3. Un lazo de la curva 8 a 2y 2 = a2x 2 - x 4 R. (na2/4 ) u 2
4. 6azx y = x 4 + 3a 4 desde x = a hasta x = 2a R. (47rra2/16) u 2
5- / O ) = - x 3, x e [0 ; 2 ] R. ^ ( 1 7 3/2 - l ) u 2
6. y 2 + 4x = 2 ln y desde y = 1 hasta y = 2 R. (IO tt/ 3 )u 2
7. x = a c o s 3t, y = a s e n 3t /?. (127ra2/ 5 ) u 2
8. y = e ~x , x > 0 R. ;r[V 2 + ln ( l + V 2 ) ] u 2
9. x = etsen t, y = e ceos t desde t = 0 hasta t = |
R. 2nyÍ2(en - 2 )/ 5 u 2
10. y = e - *, x > 0 R. ^ [V 2 + l n ( l + V 2 ) ] u 2
11. x = a (e o s t + ln ( t a n | ) ) , y = a sen t fi. 47r a 2u 2
12. y = ta n x desde (0; 0) hasta (£ ; l ) /?. t t ( V s - V 2 + l n ^ + 2
V4 ' V V5 + 1
13. E l lazo de la curva 9 a y 2 = x ( 3 a - x ) 2 R. 3 n a 2u 2
14. x 2 + ( y - /j) 2 = a 2, 0 < a < b (toro de revolución) R. 4 n 2abu
x 3 1
15- y = y + 2 ¿ ‘ x e t1; R ■(208rr/9)u2
16. y = 2x, x e [0 ; 2] r . 8 n V 5 i¿2
17. y 2 = 4 a x desde x = 0 hasta x = 3a R. (56/ra2/ 3 )u 2
APLICACIONES DE LA INTEGRAL DEFINIDA
E JE R C IC IO S
2
II. Halle el área de la superficie generada por la rotación en torno al eje y, de cada
una de las siguientes curvas
1. x = y 3 , y 6 [0; 3] R. — [(7 3 0 )3^2 - l ] u
2. 6 a 2x y = x 4 + 3 a 4 desde x = a hasta x = 3 a R. (2 0 + ln 3) n a 2u 2
213
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-220-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
3 . 2 y = * V F ^ T + l n ( * - V F ^ T ) , x e [ 2 ; S ] K . 7 8 U U 2
4. x 2 + 4 y 2 = 16
5. y - x 2 , x £ [1; 2]
6. y = x4/3, x e [1; 8]
III. H alle el área de la superficie de revolución form ada cuando la curva indicada
gira alrededor del eje dado.
1. y = x 3/z , x G [1; 8]; alrededor de y = 1
2 V = í l + _ L ( x £ [1; 2]; alrededor de y = 1
' ^ 3 4x
3. y = x 3, x 6 [1; 2]; alrededor de y = - 1
4. y = ln (x - 1 ), x G [2; e2+ 1]; alrededor de x = 1
5. y = 4 + e x, x G [0; 1]; alrededor de y = 4
6. y = 2 x , x £ [0; 2]; alrededor de y = - 1 R - 1 2 V 5 ttuz
4.6MOMENTOS Y CENTROS DE MASA (ó CENTROS DE GRAVEDAD)
E l momento de masa de una partícula respecto a una recta L se define com o el
producto de su m asa y su distancia a la recta L. A si, si m es la m gsa de la particu
y d su distancia a la recta L Fig. 4.60, entonces el momento de la partícula
respecto a la recta L está dado por
Ml = m d
Fig. 4.61
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-221-320.jpg)
![Mx
•
Es conveniente considerar la partícula localizada en un plano de coordenadas y
determinar el mom ento de la partícula respecto a un eje de coordenadas ( o a una
recta paralela a un eje de coordenadas). E n este caso se usan las distancias
dirigidas, así el mom ento será positivo o negativo o cero, según la ubicación de la
partícula; por ejemplo si la partícula de masa m está en el punto ( x ; y ) Fig. 4.61 ,
entonces sus m om entos Mx y My respecto a los ejes x e y, respectivamente son
Mx = m y , My = m x
Si un sistem a de n partículas de m asas m 1, m 2l..., m n están situados en los
puntos ( * ! ;y i), (x 2; y 2), (x n ;y n) respectivamente, los m om entos Mx y My
del sistema de n partículas se definen como
n n
= ™ ¡y ¡ - M y = ]jrrriiXi (I)
í= l i= 1
El centro de m asa o centro de grave dad de un sistema de partículas es un punto
P(x;y) tal que, supuesto que la masa total m del sistema esta concentrada en el
punto P, los m om entos de P y del sistema coinciden.
Si el sistema de m partículas de masas m u m 2, ■■■, m n ubicadas en los puntos
(x'<yi),f e ) y2). - (xn>Vn) tienen su centro de gravedad en el punto P{x; y ) y
que la m asa total del sistema es
n
m = ^ mi
i= i
entonces los m om entos Mx y My de P están dados por
Mx = m y , My = m x
Luego, de (I) se obtiene
n n
APLICACIONES DE LA INTEGRAL DEFINIDA
= m¿y; y m x = ^m y
i= l ¡=1
De donde resulta
_ Z "= 1m ¿x ¡ _
x = -------------- y y=--------------
m m
En resumen , si Mx y My son los momentos de un sistema de partículas respecto
;i los ejes x e y respectivamente y P (x ;y) es el centro de gravedad o centro de
masa del sistema, entonces
My Mx
* = -T y = - f (II)m m
donde m es la m asa del sistema.
2 1 5www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-222-320.jpg)

![U t L A 1ÍN 1 t O K A L U t , r 1 ÍN 1U A
respectivamente. Luego,
Mx = (2 1 p ) ( y ) + (6 0 p )(6 ) + (1 2 p ) = ^ p
/13 9 6 9
My = (2 1 p ) ( y ) + (6 0 p ) ( S ) + (1 2 p )(8 ) = — p
Por tanto, el centro de m asa (x ;y ) de la lámina está dado por
9 6 9
_ My - J - P
x = ^ = = 5 ,2 0 9 6 7 7 4 1 9
m 93 p
1 1 9 7
~ 2 ~ P
y = — - = — = 6 ,4 3 5 4 8 3 8 7 1
' m 9 3 p
Sea F una lám ina hom ogénea cuya densidad es constante e igual a p.
Supongam os que F es la región limitada por las gráficas de:
y = /(*), y = a(x), x = a , y x = b
donde f y g son funciones continuas en [a ;b ] y / ( x ) > g(x), V x G [a;fr]
(Fig. 4.63)
Sea P = {x1, x 2, ■■■,xn} una partición de [a;b] y c¡ es el punto m edio de
[x¿_ x; x¡] , entonces se tiene que:
m = p [/ (c ,) - 5 (c¡)]A ¡x , i = 1,2,......n (A ix = x¡ - x ^ )
es la masa del i-ésim o rectángulo som breado en la figura 4.63
2 1 7www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-224-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
lil centro de gravedad del i-ésim o rectángulo se encuentra en el punto
( f ( c¡) + g (c¡)>
[ Ci) 2
Sustituyendo cada rectángulo por un punto material y localizando la m asa de cada
rectángulo en su centro de gravedad se obtiene que los m om entos de m asa de los
n rectángulos, determinados por la partición, respecto a los ejes x e y son:
Mr
M,
lí /l
Z ™ ¡y¡ = p[/(c¡) - 5(c¡)]
/(c¡) + g ( a )
AjX
Luego, el centro de gravedad (x ; y ) estará aproximadamente en el centro de
gravedad de los rectángulos determinados por la partición, es decir:
x
My _ P'Z’j=iCi[f(ci) - g j c ^ A j X
m pEH iE /(c¡) - S(c¡)]A¡*
Mx I p i u m c d r - i g í c d ] 2} ^
y X m ~ p l U l f i c d - g i c ^ x
Pasando al límite cuando ||P|| -» 0, se obtiene que las coordenadas ( x ; y ) del
centro de gravedad de la lámina F están dadas por
Ja * [/(* ) - g(x)]dx ^ _ ^Jq{[/(*)]2 - to(*)]2}
£ [ f t o - g ( x ) ] d x A y t f f ( . x ) - g ( x ) ] d x
C om o se observa, las coordenadas del centro de m asa de la lám ina hom ogénea no
dependen de su densidad p, sólo depende de su forma. Usualm ente el centro de
m asa de una lám ina se denom ina centro de gravedad o centroide, reservando el
término centro de m asa para un sólido.
Observación 1S
a) Si la región plana F es simétrica con respecto a la recta x = x0 , entonces
x = X0
b) Si la región plana F es simétrica con respecto a la recta y — y 0 , entonces
y = yo
2 1 8
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-225-320.jpg)
![Observación 16 Si la regiónplana F esta limitadopor las gráficas de:
x = f ( y ) , x = g (y), y = c , y = d
donde f y g son funciones continuas en [c; d] y f ( y ) > g (y ), V y g [c;d ]
l'ig. 4.64, las coordenadas del centro de gravedad (x; y ) de la región F son
APLICACIONES DE LA INTEGRAL DEFINIDA
_ _ 2/cd{[/(y)32-[g(y)]2}dy
/,d[/ (y ) - g ( y ) ] d y
~ -= C y t f W - 9 ( y ) ] d y
CifXy) -g(y)d y
Ejem plo 42 Encuentre el centroide de la región acotada por las curvas y = x 3 ,
y = 4x en el primer cuadrante. ,
Solución
El área y los m om entos con respecto a los ejes x e y de la región son
A(R) = í (4x - x 3) d x = 4
Jo
_2 2
My = i x [ f( x ) - g ( x )]d x = í x(4x - x 3)dx = ^
Jo 15
Mx =z2 ¡ 0 “ Í9 (x)]2} d x = ^ J ( 1 6 x 2 - x ü)dx =
256
J T
_ My 6 4 / 1 5
Luego, x = — = ---------
m m
Mx 2 56 / 21
„ , /16 6 4
l’or tanto, el centroide es P — :—
V15 21/
219www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-226-320.jpg)
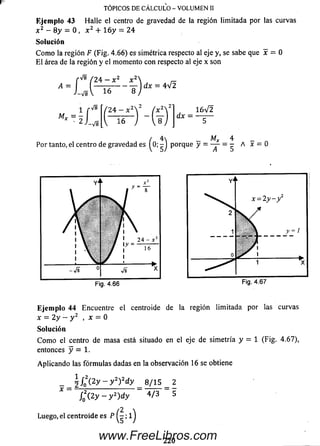
![(CJemplo 45 Determ ine el centroide de la región plana limitada por las curvas
y = / ( * ) . y = - x 2 , x = - 1 , x = 2, donde
f ( x ) = í 1 ~ x ’ x ^ °
n ) l x 2 + 1, x > 0
Solución
La región se ilustra en la Fig. 4.68. D ividiendo la región en dos partes se obtiene
APLICACIONES DE LA INTEGRAL DEFINIDA
A = í ( í - x + x 2)d x + f ( x 2 + 1 + .
J- 1 J0
11 2 2 55
M,
16 11 _ 71
15 + ~3~ — 15
= 2 / K 1 “ * ) 2 “ x *]dx + + ! ) 2 “ x *~idx
f ° r 2 13
- x ( l - x + x 2) d x + x (x 2 + 1 + x 2)dx = ------+ 1 0 =
J-i J0 12
1 07
~12
_ 107/12 _ 71/15 ^ , /107 1 4 2
,uego, x - ■ , y = -=— r , de donde el centroide es P ----- ;------ )
55/6 ' 55/6 V110 275/
Fig. 4.68
Eje m plo 46 H alle el centro de gravedad de la región infinita, en el primer
cuadrante, com prendido entre la curva y = x e~x y el eje x.
So lu ción
La región se ilustra en la Fig. 4.69. Luego, se tiene
A
J
" +CO
x e~x dx = lim [ - x e~x - e~x]o = 1
o t-*+0°
2 2 1www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-228-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
+00 r+00
My
/*i-to /■ + »
= I x f ( x ) d x = I x 2e~xdx
Jo Jo
= lim [-x2e * —2xe * —2e *]£ = 2
t->+°0
i r +”
Mx=-J [x2e~2 x -Q]d.x‘ X
Jo
1 r 1 1 1 i* 1
= - lim — - x 2e 2x —- x e ~ 2x —- e ~ 2x¡ = -
2 t-.+« L 2 2 4 J0 8
My _ MX 1
Luego, * = T = 2 . y = T = 8
Por tanto, el centro de gravedad de la región es P ^2;
Teorem a (Teorem a de Pappus para volúmenes)
S i un sólido S es obtenido al hacer rotar una región plana F (Fig. 4.70) en torno de
una recta del m ism o plano, que no sea secante a la región F, entonces el volum en
de S es igual al.área de la región F m ultiplicado por 2nr, siendo r la distancia del
centro de gravedad de la región F al eje de rotación, esto es,
V = 2nr. A
donde A es el área de F.
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-229-320.jpg)
![APLICACIO NES DE LA INTEGRAL D EFIN IDA
Ejemplo 47 Calcule el volumen del sólido 5 generado por la rotación de la
S a a P ° rlaP aráb 0,a y = * 2 y ,areC ía y = * + - 2 en tomo a esta
Solución
Para determinar el centro de gravedad.de la región F (Fig. 4.71) se tiene
A (F) = í (x + 2 - x z)d x = -
J-1 2
My = í x (x + 2 - x 2)d x = -
•'-i 4
Mx = í [(x + 2 y - x 4] d x = —
¿ J - i 5
Por tanto, el centroide (x; y ) de la región tiene las coordenadas
A ~ 2 ‘ y _ T " 5
Calculando la distancia r del punto C ^ a la recta y = * + 2 se tiene
r = ^ ~ y + 2l = l l ~ l + 2|_ 9V2
V i + 1 V2 20
Luego, por el teorema de Pappus, el volum en del sólido S es
V = 2ur. A = 2n Q = «3
Y' i.
l F
1 Vv.7,
i i i 1 v
f
¡ L
. / 1 %
/ 1 /
Y 1 /
y ( V s "x
' ►(-! ;0)
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-230-320.jpg)

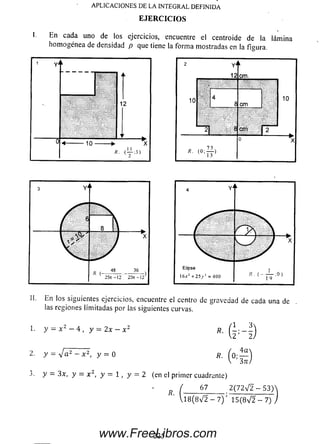


![TÓPICOS DE CÁLCULO - VOLUMEN II
5, La región limitada por las gráficas de y = x 2 , y = 5 gira alrededor de una
recta oblicua que pasa por el punto ( - 1 ; 0). Halle la ecuación de la recta si el
volum en generado es igual a (4 0 V 5 n ) u 3 R. 3 x + 4 y + 3 = 0
IV . E l centro de gravedad ( x ; y ) del arco de una curva (hom ogénea), cuya
ecuación es y = f ( x ) con x 6 [a; b] , donde / es una función con derivada
continua en [a; b] , está dado por
_ f c x j i + i f ' i x w d x f / w y i + i / ' M P d *
j ^ i + [ f ( x ) Y d x ' y jab y i + [f'( x ) ) 2 dx
U sando estas fórmulas, determine el centro de gravedad de las curvas cuyas
ecuaciones son
2,------------ / 2 a
1. y = V a 2 - x 2 R. —
x ( a ( e 4 + 4 e 2 - 1)
2. y = a c o s h - , x £ [ - a ; a ] R■ (0 ;
a ' 1 ' J V ' 4e(e2 -
/ '
3. x = a (t - sen t ) ,y = a ( l - eos t) ,t e [0;27r] R. (?ra;-
4 a
3 /
r Til /2a 2 a
4. x = a c o s 3t , y = a s e n 3t , t e [ 0 ; - j R.
228
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-235-320.jpg)
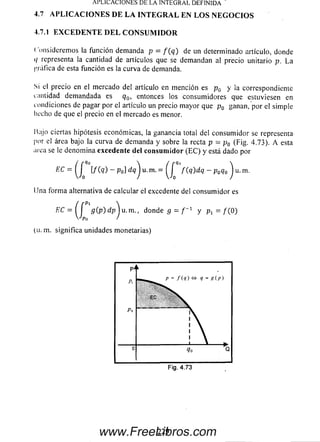
![Considerem os la función oferta p = f ( q ) de un determinado artículo, donde q
es la cantidad de artículos ofertados al precio unitario p. L a gráfica de esta
función es la curva de oferta.
S i el precio en el mercado del artículo en m ención es p 0 y la correspondiente
cantidad ofertada es q0, entonces los productores que estuviesen en condiciones
de vender el artículo a un precio menor, ganan, por el sim ple hecho de que el
precio en el m ercado es mayor.
Bajo ciertas hipótesis económicas, la ganancia total del productor se representa
por el área sobre la curva de oferta y bajo la recta p = p 0 (Fig. 4.74). A esta área
se denom ina excedente del p ro d u c to r (E P ) y está dado, por
Ep = ( f [ P o - f ( ‘})]dqSju .m .= ^p0q0 - J f(q)dqju.m .
U n a form a alternativa de excedente del productor es '
EP = ( í 9 (.P)dp^u.m., donde g = / -1 y Pi = /(O )
TÓPICOS DE CÁLCULO - VOLUMEN II
4.7.2 EX CED EN TE D EL PR O D U C TO R
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-237-320.jpg)
![l' Jt'iiiplo 49 S i la función demanda es p = 9 - a 2 v o - 5 Hallp m ^ )
ili'l consumidor. q > Po “ Halle el cxccdcnie
A P L IC A C IO N E S D E LA IN T EG R A L D E F IN ID A ’
Sol ución
I .i región se muestra en la figura 4.75. Con la ayuda de ¡a figura se obtiene
EC = f (9 — q 2) — 5jcJ<7 =
-Ai
16
i!, m.
excedente del productor.
Solución
a región se muestra en la figura 4.76. A sí, resulta
EP — f [16 - (4 + 3 q 2)] dq = 16 u.
Jo
m.
Ejem plo 51 Las funciones de demanda y de oferta, en situación de competencia
perfecta son p = 227 - - q 2 y p = 2 + 2q2 respectivamente. Determ ine el
el correspondiente excedente del consum idor y el excedente'de productor.
Solución
LI precio en el mercado y la correspondiente cantidad está determinado por el
punto de equilibrio E (Fig. 4.77). E l punto de equilibrio es la intersección de las
curvas de oferta y de demanda, esto es,
2 2 7 4 - 2 + 2q2 => q 2 _ 1 0 0 => qe = 1 0 , de donde pe = 202
231
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-238-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
Fig. 4.78
Luego,
500
dq = — 11. m.
r 10 1
EC = I 227 - j q 2 ~ 202
J0 4
r 1° 4000
EP = J [202 — (2 + 2q2)] dq = - u.m
Eje m plo 52 L a cantidad vendida y el correspondiente precio, en situación de
m onopolio, se determ inan por la función de dem anda p = — (10 — qY y el costo
3
total es C = — + 5a de tal m anera que se m axim ice la utilidad. Determ ine el
4-
correspondiente excedente del consumidor.
Solución
L a utilidad es U = I —C , / = in gre so y C = costo total
W = 0 =* /' - C' = 0 =» lMg = CMg
"L a utilidad se m axim iza si el ingreso m arginal (/' = IMg) es igual al costc
m arginal (C' = CMg)”.
C om o / = pq donde p = precio de venta y q = cantidad vendida, entonces
1 3 9
/ = -(10 - q)2q =>IM g = 2 5 - 10q + -(?
3 3
Luego IMg = CMg => 25 - lO q + - q 2 = - ^ 2 + 5 => q = 2
En q = 2 , la utilidad es m áxim a porque U " (2) = - 1 0
Por tanto,
r 2
r2ri i 26
= j j - ( i 0 - q ) 2 - 16j de/ = Y (F ig .4 .7 8 )
2 3 2
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-239-320.jpg)












![COORDENADAS POLARES
III) Extensión. Se determina la variación de r y 8
IV ) T abu lación . Se tabulan los valores de r y 8.
V ) T ra z a d o de la gráfica. E n un sistema de coordenadas polares (es preferible
usar la roseta polar) se localizan los puntos obtenidos y se traza la curva con
la inform ación obtenida en la discusión.
E jem plo 6. Determ ine si son simétricas o no respecto al eje polar, al eje n / 2 y al
polo, las curvas cuyas ecuaciones son:
a) r = 4 eos 8 + 2 (caracol) b) r 2 = 9 [sen + l]
c) r — 3 (1 + c o s 0 ) (cardioide)
So lu ción
a) i) Respecto al eje polar. Reem plazando en la ecuación (r; 8) por (r; - 0 ) ,
se obtiene que r = 4 c o s ( - 0 ) + 2 = 4 c o s 0 + 2. Por tanto, la curva es
simétrica con respecto al eje polar.
ii) Respecto al eje n /2 . A l reemplazar (r; 8) por ( - ( - l ) nr; - 8 + nn), se
tiene que - ( - l ) nr = 4 c o s ( - 0 + nn) + 2.
S i n es par => - r = 4 eos 8 + 2 (varía).
Si n es impar => r = 2 - 4 eos 8 (varía).
Luego, la curva no es simétrica porque la ecuación varía para todo n G TL.
iii) Respecto al polo. A l reemplazar (r; 8) por ( - ( - l ) nr; 8 + nn), se tiene
que - ( - l ) n = 4 c o s(0 + nn) + 2.
S i n es par => - r = 4 eos 8 + 2 (varía)
Si n es impar => r = 2 - 4 eos 8 (varía)
L a curva no es simétrica con respecto al polo. L a gráfica del caracol
r = 4 eos 8 + 2 se muestra en la figura 5.10.
b) i) Respecto al eje polar. Para n = 2, es decir, reemplazando (r; 8) por
(r; 2n - 8), se tiene
Por tanto, la curva es simétrica con respecto al eje polar.
ii) Respecto al eje n/2 . Para n = 2, es decir, reemplazando (r; 8) por
( — r; 2n —8), se tiene
Por tanto, la curva es sim étrica con respecto al eje n/2.
iii) Respecto al polo. L a ecuación no varía al reemplazar (r; 8) por ( — r; 8)
(para n = 0). Luego, la curva es simétrica respecto al polo y su gráfica se
muestra en la Fig. 5.1 1.
245www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-252-320.jpg)
![c) i:i cardioide r = 3 ( l + c o s 0 ) es simétrico con respecto al eje polar. N o es
simétrico respecto al eje n / 2 ni respecto al polo (verificar).
I,a gráfica del cardioide r = 3 ( l + c o s0 ) se muestra en la Fig. 5.12.
TÓPICOS DE CALCULO - VOLUMEN II
110“ ‘
.
*"*N A V "
i / V ^ s ;
i . . r* l
✓ S/
K j I ' 1 *■*"...I i ' jJ
/ y -s __
2 4 0 °
- x
—*^
cosO +2
i
/ .
jk X ^ *
/ ' > &
i . .
V
" 7
s¡§-3 N g Q /
a /
A
r = 3 (l + co s0)
E je m plo 7. Discutir y graficar la ecuación r —4 eos 9 + 2 (caracol).
So lu ción
Por la periodicidad del coseno, es suficiente considerar 8 6 [0; 2n].
I. Intersecciones
a) C on el eje polar. Reem plazam os 9 = nn en la ecuación y se tiene
r = 4 c o s(n 7 r) + 2.
Si n es par => r = 6 => (6; 0)
Si n es impar => r = — 2 => ( - 2 ; n)
b) C on el eje n /2 . Reem plazam os 9 = (tt/2 + nn) en la ecuación y obtenemos
r = 4 c o s (7t / 2 + nn) + 2
S i n es par => r = 2 => (2; n / 2 )
S i n es impar => r — 2 => (2; 3 n /2 )
246www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-253-320.jpg)
![c) C on el polo. Haciendo r = 0 en la ecuación, se obtiene 0 = 4 eos 6 + 2 ó
eos 9 = — 1/2. Luego, 8 = 2 n /3 V 9 = 4 n /3 . L a curva pasa por el polo.
II. Sim etrías. E n el ejemplo 6 hemos visto que este caracol es sim étrico
solamente respecto al eje polar.
III. Extensión, fl £ M A - 2 < r < 6,
IV. T a b u lac ió n
COORDENADAS POLARES
9 0 n / 6 7T/4 n /3 n / 2 2 n /3 3 n /4 S n /6 7T
r 6 5,5 4,8 4 2 0 - 0 , 8 - 1 , 5 — 2
V. T ra z a d o de la gráfica. L a gráfica se muestra en la figura 5.10.
se" © + 1
E je m p lo 8. Discutir y graficar la ecuación r 2 = 9
Solución
Procedemos de manera sim ilar a lo realizado en el ejemplo anterior.
I. Intersecciones
a) C on el eje polar. 9 = nn => r 2 = 9[sen(n7r/2) + 1],
Si n = 0 => (3 ;0 ) y ( — 3; 0). .
Si n = 1 => (4,2; 7r) y (— 4,2; 7r).
Si n = — 1 => (0; — 7r).
7T 71
b) Con el eje 6 = - + nn
¿ ¿t
( + n n
sen — + 1
Si n = 0 => (3,9; n / 2 ) y (-3 ,9 ; tt/2).
Si n = 2 => (1,6 ; S n/2 ) y ( - 1 , 6 ; Sn/2).
c) C o n el polo, r = 0 => 9 = 3 n , 9 = 7n.
II. Sim etrías. L a curva es simétrica con respecto al eje polar, al eje n / 2 y al
origen (ver ejemplo 6).
III. Extensión. 9 £ K y - 3 V 2 < r < 3V2.
IV. T a b u lac ió n (Ejercicio para el lector. Considerar que el período de la función
es 47r)
V. T ra z a d o de la gráfica. L a gráfica se muestra en la figura 5.11.
247www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-254-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
Ejem plo 9. Trace la gráfica de r = 1 — [2 sen 2 0 ] , 0 e [0; n].
Solución
D ivid im os convenientemente el intervalo [0; 7r] de m odo que |[2 sen 2 0 ] tome un
solo valor entero en el subintervalo considerado.
Si 0 £ [0; 7T/12) => 0 < 2 sen 20 < 1 => |2 sen 20] = 0 => r = 1.
Si 0 e [tt/12; 7t/4) => 1 < 2 sen 20 < 2 => [2 sen 20] = 1 => r = 0.
Si 0 = ti/4 = ^2 sen 20 = 2 => [2 sen 2 0] = 2 =* r = - 1 .
Si 0 G <7t/4; 5tt/ 12] => 1 < 2 sen 20 < 2 => 12 sen 2 0] = 1 => r = 0.
Si 0 6 <5tt/12; jt/2] =* 0 < 2 sen 20 < 1 =* 12 sen 20] = 0 => r = 1.
Si 0 e (j t / 2; 7tt/12] =* - 1 < 2 sen 20 < 0 => 2 sen 2 0] = - 1 => r = 2.
Si 0 6 <7tt/1 2; H tt/ 1 2 ) => - 2 < 2 sen 20 < - 1 =» [2 sen 2 0] = - 2 => r =
Si 0 e [1171/12; 7r> => - 1 < 2 sen 20 < 0 => 12 sen 2 0] = - 1 =» r = 2.
Si 0 = 7r => 2 sen 20 = 0 => [2 sen 2 0] = 0 => r = 1.
La gráfica se muestra en la Fig. 5.13.
5.7 I N T E R S E C C I Ó N D E C U R V A S E N C O O R D E N A D A S P O L A R E S
P ro p o sició n 1. S i r = / ( 0 ) es la ecuación de una curva en coordenadas polares,
entonces
( - l ) n r = / ( 0 + 7i7r) , n £ Z (1 3 )
es también la ecuación de dicha curva.
Considerando esta proposición, para hallar la intersección de dos curvas cuyas
ecuaciones en coordenadas polares son
r = f ( 6 ) y r = g ( 8 )
se siguen los siguientes pasos:
1. Se obtienen todas las ecuaciones distintas de las dos curvas aplicando (13) a
cada una de ellas.
r = f ( 9 ) , r = A ( 0 ) , r = f 2( 9 ) , ...
r = g ( 9 ) , r = g ^ G ) , r = g 2(8 ) , ...
2. Se resuelven, para r y para 9, las ecuaciones simultáneas
r = m fr = /i(0) [r = f(6)
r = g ( 9 ) ' l r = ^ ( 0 ) ’ [ r = 5 l (0 ) ’ eiC'
248www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-255-320.jpg)


![5.8 D E R I V A D A S Y R E C T A S T A N G E N T E S E N C O O R D E N A D A S
P O L A R E S
Sea r —f (0 ) la ecuación de una curva. D e las fórm ulas
(x = f ( 9 ) eos 9
(y = / ( 0 ) s e n 0
que son las ecuaciones paramétricas con parámetro 0, de donde
C O O R D E N A D A S PO LA R ES
x = r e o s 9 A y = r sen 6 se obtienen P
(y =
d y
d y _ ¿e_ d y _ f ' { 9 ) sen 8 + / ( 0 ) eos 9
dx dx^' dx / '( 0 ) eos 9 —/ ( 0 ) s e n 9
dG
(1 4 )
C om o sabemos, esta derivada es la pendiente de la recta tangente a la curva en el
punto (x ; y ), es decir,
d y
— = tan a
dx
(1 5 )
donde a es el ángulo de inclinación de la recta tangente a la curva.
Sea P ( r 9 ) el punto de tangencia y /? el ángulo que forma el radio vector O P y
la recta tangente. Exam inarem os los siguientes casos:
En el caso (a): a = 9 + p => p = a —9
En el caso (b): p = a + n - 9 => p = n + (a - 9), dedonde:
tan p = tanfrr + (a - 0 )] = ta n (a - 9)
L o que significa que en am bas situaciones se verifica tan p = ta n (a - 0), es
decir,
tan p =
tan a —tan 9
1 + tan a tan 9
(1 6 )
251www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-258-320.jpg)

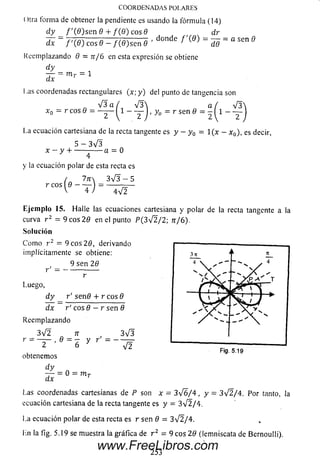


![TÓPICOS DE CÁLCULO- VOLUMEN II
9. 3 x 2 + 4 y 2 - 6x - 9 = 0 R. r 2( 3 + sen20 ) = 3 (2 r eos 0 - 3 )
1 0 .2 x y = a 2 R- r 2 sen 20 - a 2
11. x 2 - y 2 = a 2 R. r 2 eos 26 = a 2
IV . H alle las ecuaciones rectangulares de
1. r = a sen 9 - b c o s O Æ. x 2 + y 2 + b x - a y = 0
2. r 2 = a 2 eos 20 R. ( x 2 + y 2) 2 = a 2( x 2 - y 2)
3. r ( l - eos 0) = 4 R. y 2 = 8 (x + 2)
4. r ( 2 - eos 0) = 3 R. 3 x 2 + 4 y 2 - 6x - 9 = 0
5. r ( l - 2 eos 0 ) = 4 R. 3 x 2 — y 2 + 1 6 x + 16 = 0
6. r = a ( l — eos 0) R. ( x 2 + y 2 - ax) = a 2( x 2 + y 2)
7. r 2 eos 2 0 = 3 fí. x 2 - y 2 = 3
8. r = 2 eos 20 R. (x 2 + y 2) 2 = 2 ( x 2 - y 2)
9. r sen 20 = 4 R. x 2y 2 = 4 ( x 2 + y 2)
10. r = a sec 0 + b R. (x - a ) 2( x 2 + y 2) = ¿>2x 2
11. r sen20 = 4 eos 0 Æ. y 2 = 4x
12. r = sen 20 ñ. (x 2 + y 2) 3 = 4 x 2y 2
V . Ejercicios diversos.
1. Dem uestre que el área del triángulo de vértices Cril ^ i). (r 3 ^ 3 )
está dada por
1 rsen (02 - 0 i) sen (03 - 02) sen (0x - 0 3)]
r * ™ í— í — + — ñ — + ü 1
2. Halle la longitud de los lados y el área del triángulo de vértices
a) (1; 7t/ 3) , (2; ít/ 6) y (3; — tt/6)
fí. J 5 - 2 V 3 , V 7 , V lÓ , ^ ( 3 V 3 - 2 )
b) (2; tt/ 8 ) , (4 ; 3 rr/8 ) y ( - 1 ; 7 tt/ 8 ) _________
/?. 2 j s ^ 2 V I , j 5 - 2 V 2 , V Í 7 , ^ ( 5 V 2 - 4 )
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-263-320.jpg)

![a) Halle la ecuación de la elipse con foco en el polo, excentricidad e = - y
directriz perpendicular al eje polar en el punto ( — 4; 0).
4
R. r =
TÓPICOS DE CÁLCULO - VOLUMEN II
2 —eos 8
b) Halle la ecuación de la parábola con foco en el polo y directriz
perpendicular al eje polar en el punto ( — 3; 0).
R. r
1 - eos 0
c) Describa y grafique la curva r =
16
5 + 3 sen 6
R. elipse
V I.T ra ce la gráfica de cada una de las ecuaciones siguientes.
1. r = 5 sen 0 + 4 c o s 0
3. r eos 0 = 6
5. r 2 = 16 sen 20
7. r ( 1 + se n 0 ) = 8
9. r 2c o s30 = a sen 0
11. r = a se n 2 -
13. r = a 0, espiral de Arquím edes
15. r = a ( l + eos 0), cardioide
17. r 2 = a 2se n 20, lemniscata
19. r = 4 eos 30, rosa de 3 pétalos
21. r = a sen 30, rosa de 3 pétalos
23. r = a eos 20, rosa de 4 pétalos
25. r = a eos 40, rosa de 8 pétalos
27. r = a eos 50, rosa de 5 pétalos
28. r = a ( 2 + eos 0), caracol de Pascal.
29. r = a ( l - 2 eos 0), caracol de Pascal
30. r = 12 + 3 sen 2 0 ]
2. r sen 0 = 4
4. r z sen 2 0 = 16
6. r ( 2 — cos 0 ) = 4
8. r ( l - 2 cos 0 ) = 4, hipé'bola
10. r = 2 a tan 0 sen 0, cisoide
3 0
12. r = a se n J -
14. r = e a0, espirai logaritm ica
16. r = a ( l - cos 0), cardioide
18. r 2 — a 2 cos 20, lemniscata
20. r 2 — 4 r + 3 + 2 cos 0 = 0
22. r = a se n 20, rosa de 4 pétalos
24. r = a se n 4 0, rosa de 8 pétalos
26. r = a se n 50, rosa de 5 pétalos
2 5 8www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-265-320.jpg)
![' 2'
3 tt>
R. ( 2 V 2 ; Í ) ; ( 2 V 2 ;^ )
COORDENADAS POLARES
31. |r| = 3 eos 2 0 , 0 e [0; tt]
32. |r| = - 3 eos 29 , 9 e [0; rr]
V II. Ejercicios sobre simetrías.
1. Determ ine la condición para que una curva sea simétrica con respecto al
eje 7r/4.
2. Determ ine la condición para que una curva sea simétrica con respecto al
eje 7T/3.
V IH . Halle los puntos de intersección de los siguientes pares de curvas
1. r sen 9 = 2 a , r eos {9 - = a R. ( 2a;
2. r = 2 esc 9 , r = 4 sen 0
3. r = a , r = 2a eos 20
4. r = a ( l - e o s 0 ) , r = a c o s 0 /?. y e|p 0 |0
5. 3 r = 4 eos 0 , r ( l + eos 0 ) = 1R. (2/3; ± tt/ 3 )
6. r = 4 tan 0 se n 0 , r = 4 eos 0
7. r 2 sen 20 = 8 , r eos 0 = 2
8. r = 1 + c o s 0 , 2 r = 3
19. r = - sec¿ - , r = 2
2 2
0 1
10. 3 r = 4 eos 0 , r e o s2 — = —
2 2
11. r = l + c o s 0 , 2 r ( l - c o s 0 ) = l
12. r eos 0 = 4 , r = 10 sen 0
13. r = a( 1 + se n 0 ) , r = a ( l - sen 0 )
14. r = 3 + e o s 4 0 , r = 2 - c o s 4 0
15. r = 2 + eos 20, r = 2 + sen 0
259www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-266-320.jpg)


![Ivn esta sección deducirem os una fórm ula que permita obtener el área de una
región F (Fig. 5.22) limitada por una ecuación polar, esto es,
F = {(r; 0 ) É l 2 / a < 9 < p , 0 < r < / ( 0 ) }
donde /: [a; /?] -» E es una función continua y no negativa.
TÓPICOS DE CÁLCULO - VOLUMEN II
5.10 ÁREAS EN CO O RD EN AD A S PO LA RES
Fig. 5.22 m g.
En términos sim ples, F es la región comprendida entre las gráficas de
r = / ( 0 ) , eje a , eje /? (co n a < /?)
Sea 0o e [ a p ] y sea A(0O) el área del sector limitado por la curva r = f ( 9 )
y por las rectas 9 = a y 8 = 90. Sea 60 + A0 6 [a; /?], con A 0 > 0, y
. m = m ín f { 9 ) A = m áx / ( 0 )
0o<e<eo+Ae tío<0íeo+A0
El área A(60 + A9) - A(90) está comprendida entre las áreas de ios sectores
circulares de radios m y M (Fig. 5.23). Para A0 > 0 se tiene
m 2A9 M2A9
Luego.
< A(80 + A9) - A(90) <
m 2 ^ A (90 + A 9) —A(90) ^ M2
~ Y ~ A 6 “ ~2
C om o f 2/ 2 es continua en [0O; 0 O + A 0 ] , por el teorema de los valores
intermedios, existe 9 G [90 90 + A 0 ] tal que
f 2(9) A (9n + A 0 ) — A(90)
2 A 9
Por la continuidad de f 2/2 en 0 O, se sigue que
A{9a + A0) - A(90) f 2(90)
lim
A9
2 6 2www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-269-320.jpg)
![C O O R D E N A D A S PO LA RES
Procediendo de m odo análogo, para A0 < 0 . se tiene
lim A (°o + M ) - M Q 0) f 2(Q0)
A 0 -0 - AO 2
l’or tanto,
A ' ( 9 ) = ~ y ^ , V 0 € [ a , P ( * )
l’or consiguiente, de (*) se deduce que la fórm ula para hallar el área de la región
/■' expresada en coordenadas polares es
1 [P
a ^ = 2 ¡ f 2W 0
Observación 5. Sean f , g: [a; /?] -> M funciones continuas en [a, p] tales que
() S g( 8 ) < f ( 9 ) , V 6 e [a;P], y sea F la región limitada por las gráficas cíe
>' = 9 ( 0 ) , r = f ( 9 ) y ¡as rectas 0 = a y 0 = fJ (Fig. 5.24). Entonces el
área de la región F está dada por
A{F) = f [ f 2(6) - g d ) ] d O
Jir
l.jem plo 17. Calcule el área de la región /•’ limitada por la curva r - 2 + eos U y
los ejes 0 = 0 y 0 = n/ 2.
Solución
I .a gráfica de la región F se muestra en la fig. 5.25.
A l aplicar la fórm ula correspondiente para hallar el área, se tiene
+ 1 6 ,
= -----
M F) = + c o s 0 ) 2 d0 = ^ J g2 (4 + 4 c o s 0 + 1-+ .™ S dd
263www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-270-320.jpg)
![Ejem plo 18. Calcule el área de la región limitada por la lemniscata
r 2 = a 2 eos 20
So lu ción
C om o la lemniscata es una curva simétrica respecto al eje polar, es suficiente
m ultiplicar por 4 el área de la región R (Fig. 5,2o). Entonces
TOPICOS DE CALCULO - VOLUMEN II
A(F) = 4
n
i r*
J 4«Jo
2 eos 29 d9
E je m p lo 19. H alle el área de la región lífnitada por lás parábolas
r ( l + eos 9) = 4 y r ( 1 - eos 0 ) - 4.
So lu ción
E n este ca¿&, una parábola es simétrica á la otra parábola con respecto al eje n / 2
(al reemplazar 9 por n - 9 efl láf' primera ecuación, se obtiene la segunda
ecuación). Estas parábola» son simétricas con respecto al eje polar y sus puntos de
intersección son los puntos 4 (4 ;7 r/ 2 ) y B (4 ;37 r/ 2 ). Considerando las
simetrías, el área de la región enjre estas parábolas (Fig. 5.27) es 4 veces el área
de la región R. En la integral se utilizará la identidad (1 + eos 9 = 2 e o s20/2).
A(F) = 4
1 f I 16 d9 _ ÍJ d9 _ [2
2 J0 ( l + c o s 0 ) 2 32 J0 [2 eos2 6/ 2] 2 J0
Ae
sec — d9
64
Eje m plo 20. Calcule el área de la región que es interior a la curva r = 2a eos 30
y exterior a la circunferencia r = a, a > 0,
So lu ción
La región se muestra en la Fig. 5.28 (parte sombreada). Para hallar el área total es
suficiente m ultiplicar por 6 el área de la región R. Entonces
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-271-320.jpg)
![COORDENADAS POI..A RES
90'
120"
150°N.
60°
/ 30"
R T l M k
r = ; a eos 39
Fig. 5.28 Fig. 5.29
I jeinplo 21. Calcule el área de la región que es interior a las curvas
V 2 r = 3 y r z = - 9 c o s 2 0
Solución
La región es la parte som breada que se muestra en la c ig. 5.29. Por sim etría se
(iene
A(F) = 4
1 [3 2 f ' i 9
- j ¡ ! (-9 c o s 2 S )d e + - l - M
4 3
3 , — ,
= - ( 6 + 7r - 3 ^ 3 ) ^
E jem plo 22. Halle el área de la región que es interior a la curva r = 3 a eos 26 y
exterior a la curva r = a ( l + eos 2 0 ) , a > 0.
Solución
La región es la parte som breada que se ilustra en la fig. 5,30. Por simetría, se tiene
A ( F ) = 4 [A(RX) + A(Rz) l . dondfe
1 f 6
i) = y [9a2cosz.29 - a2( 1 + eos 26) 2]
‘ ^ Jo
. - « ü f
^ i0
d<9
6(3 + 4 eos 4 0 - 2cos 2 0) dfl = ^
^(^2) = 2J [9a2cos22ff - a2( 1 + eos 2 0 )2]d0
(donde a es tal que eos 2a == - 1 / 4 )
= - y J [3 + 4 e o s40 - 2 c o s2 0 ]d 0 = + ~ 7 r ~ “ 3 a
3
Luego, A(F) = a 2 ( 4 7 1 + ^ ^ 1 5 —6aj u2 = (9,95 a 2) u2:
265www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-272-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
5.11 LO NG ITUD DE A RCO EN COORDENADAS PO L A R E S
Para calcular la longitud de arco de una curva expresada por la ecuación polar
r = f ( 9) , 9 6 [a;P], parametrizamos en términos del parámetro 0. A sí. las
ecuaciones paramétricas de la curva son
x = f ( B) e o s 9 A y = / (0 )s e n 8 , 9 6 [a;/?]
donde / es una función con derivada continua V 9 6 [a; /?].
A l aplicar la derivada de un producto, se obtiene
dx dy
— = f ' { 9 ) eos 9 - / (0 )s e n 9 y — = / '(0 )se !n 0 + / ( 0 ) eos 0
uu do
Entonces
ÍS) +Q ’
Luego, aplicando la fórm ula de longitud de arco de una curva dada en ecuaciones
paramétricas, se tiene c}ue la longitud de arco de r = / (9) desde 9 = a hasta
9 = ¡i está dada por ’
L = f V I / ( 0 ) P + [ / '( 0 ) ] 2 d.9
Eje m plo 23. H alle a longitud de arco de la curva r = a se n 3(0 / 3 ) , a > 0.
Solución
L a gráfica de la curva se muestra en la fig. 5.31. L a curva queda descrita si
9 6 [0; 37rJ (es simétrica respecto al eje rt/2).
6 6 0Q
Com o [/ (0 )]2 + l/ '( 0 ) ] 2 = a2 se n 5 ~ + a 2sen4 - eos2 - = a2sen4—, entonces
>J J ví
r37r { 6 f 3n , 0 a f 3n ( 2d 3an
! ! Ja2 sen4 - d9 = a sen2 — d.9 = — j (1 — eos — )d 9 = — — u
¡ . 3 i p 3 2 J„ y j / 2Jo
Fig. 5.31
266
Fig. 6.32
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-273-320.jpg)
![E jem plo 24. Halle la longitud de arco de la parte de la parábola r = a se c 2( 6 / 2)
cortada por la recta perpendicular que pasa por eí polo.
Solución
La gráfica se muestra en la fig. 5.32. Se tiene ~ n f 2 < 0 < n / 2 y
dr
¿jj = / '(Ö ) = a sec2(0/2)tan (0/2)
Aplicando la fórm ula correspondiente, se tiene
n
"2 9
secs — d9
COORDENADAS POLARES
1 = / l V [ / ( 0 ) ] 2 + [/ '( 0 ) ] 2 d9 = a f
~Z
— í ® i. ® , I ® e V-
— a sec — ta n — + ln se c— + ta n — J
l 2 2 1 2 2
2
= 2 a[V 2 + ln (V 2 + l) ] u
Ejem plo 25. Halle la longitud de la curva r = 2b tan 0 sen 0, b > 0 desde
0 = 0 hasta 0 = tt/3.
Solución
La gráfica de la curva se muestra en la fig. 5.33. C on la fórm ula de la derivada
obtenemos
dr
d9
- r' = 2b sen 0 (se c 20 + 1)
Luego,
TT
‘ 1 = l J r 2 + ( r ') 2 d9
n
= 2 b j tan 0 V s e c 20 + 3 d9
Ln la última integral hacem os el cam bio de
variable u 2 = se c 20 + 3. Entonces
2 u d u ~ 2 sec20 tan 0 d9 => tan 0 d6 -
u du
u 2 - 3
Cam biando los límites de integración, se tiene
f V? U2 du
; = 2b
J 2
L = 2b
f v u 2 du H 7 3
i ^ 3 = 2 b l i l + ^ Í > du =
2 ¿ ( V 7 - 2 ) + V 3 f c l n f - p + V ^ ( V 7 ~ V I )
l(2-V3)(V7 + V3).
. V 3 lu - V 3
u + — ln ------- -
2 u + V3
V7
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-274-320.jpg)
![5.12 V O L U M E N D E U N S Ó L I D O D E R E V O L U C I Ó N E N C O O R D E N A D A S
P O L A R E S
TÓPICOS DE CÁLCULO - VOLUMEN II
En primer lugar, querem os calcular el volum en de un sólido (Fig. 5.35) obtenido
por la rotación alrededor del eje x de un sector circular del plano xOy (Fig. 5.34)
com prendido entre los ángulos 0* y 02.
i
/
/ y
1 i A
X
Fig. 5.34
E l sector circular puede ser descrito del siguiente modo:
0 < x < r c o s 02 y fi(x) < y < f 2{x) ) sect:or entre Qt y 02
r eos 02 < x < r eos 0, .y ft (x) < y < fl(x))
donde
f x(x) = x tan 0r , /2(x ) = x tan 02, g{ x) = J r 2 - x 2
A l aplicar el método del disco, obtenemos
¡•r cos 0, rr cos0i
V
/•r eos 02 f r CO S0! | - r c o s 0 !
= .jr [f2(x)]2dx + n [g (x )l2dx — n I l A (x ) ] 2d r
Jq- *^r eos 02
r.r eos 0 2 r r c o s 0 ! f r c o s O j
= tt x 2 tan262 dx + u ( r 2 - x 2) dx - n x 2 tan201 dx
J n -¡r eos 02 0
Haciendo los cálculos respectivos, se tiene
2 n r 3
1/ = — — (eos 0! - eos 0 2) (21)
Ahora, nuestro propósito es calcular el volum en V del sólido obtenido por la
rotación en torno al eje polar de la región plana
F = ((r; 0 ) / 0 < r < f(fl) , a < 8 < (3}
donde r = / ( 0 ) es la ecuación de una curva en coordenadas polares (/ es
continua en [a; /?]) y F es la región limitada por las gráficas de la curva r =
/ ( 0 ) y los ejes 0 = a y 0 = /? (Fig. 5.36).
2 6 8www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-275-320.jpg)
![COORDENADAS POLARES
Sean 90 y 80 + A 8 dos puntos de [a;/?], con A 8 > 0. y
m = «, A M = m áx f { S )90<8<60T&e 80<8<60-rAe
I- I volum en obtenido por rotación del sector F com prendido entre 80 y 8n + A 8
(Fig. 5.37) es. según la fórm ula (21).
¿ 7n n 3 2 tzM 3
- J ~ [eos 0O- eos (0O+ A0] < V(6„ + A0) - V(80) < — - [eos 0O- eos (0O-i- A0)j
Dividiendo entre A 0 > 0 se tiene
¿711W? rc o s 0 n - eos (6>0 + A 0 ) 1 V (60 + A 0 ) - V(80) 2ttA/3 rc o s0 c - eos (6 + A fl)i
3 ‘ AS j - re----------- £ — [----------------------------- J
Com o f 3 es continua en [80;8 0 + &8], por el teorema de los valores
intermedios, existe Qx e [0O; 80 + A 0 ] tal que
A 8
2 n f 8 J eos 80 - eos(80 + A 0 )i
3 A 8
I ornando limite cuando A 8 -> 0 + , debido a la continuidad de f en 8n, se tiene
27r / 3(0 o) n
1/ j = ------- --------- sen ^
Del m ism o m odo se hace para A 8 < 0. Por tanto.
f 3(80)
V'(ßo) = -se n 0,
malmente, el volum en del sólido es V = V(ß) - V(a). esto es
2rr f ß ,
i/ = r l f í n ,)se n 8 dB
269www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-276-320.jpg)
![TÓPICOS DE CÁLCULO - VOLUMEN II
Eje m plo 26. Calcule el volum en del sólido obtenido al hacer girar el cardioide
r = a( 1 + c o s 0 ) , a > 0, alrededor del eje polar.
Solución
En la figura 5.38 se observa que para obtener el referido volum en es suficiente
girar en torno al eje polar la parte del cardioide que está en el sem iplano superior.
Entonces se tiene:
o
(1 + c o : É»)4] 71
r = a(l+ eos 0)
Fig. 5.38
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-277-320.jpg)

![las curvas r = 3a eos 20 y r = a (l + eos 20),
TÓPICOS DE CÁLCULO - VOLUMEN II
in te rio r a V 2 r = 3 y e x te rio r a ' r 2 = - 9 e o s 20^
2
18. La región es interior a j * g
R. ( 3 7 t - 9 + - V 3 j u 2
19. L a región es interior a
a > 0.
20. La región está com prendida entre la parte ex.erna e intetna de
3 e K- “ 2 ----------5 5 --------- “ 2
r = asen '5- J
21. L a región está com prendida entre las curvas:
9 n ,
a) r — i — eos 20 , r — 2 (1 eos 2 0 ),
0 < 0 ^ R- ~
b) r = 2 a eos 0 , r = 2 a sen 0
, ^ ) , 2
c) r = a se n 0 , r = a ( l i- eos 0)
d) r = 2 sen 2 0 , r = 2 eos 20 »• ( F 1)
curva.
1 r = sen 9 , 0 S [0; 2rr]
2 . r = 20 , e e lo; 2« ) «■I2W T + 4F + '" t 2 " +
^ n R- 8 a u
3. r = o(l + eos 0 ) , a > 0
4 . e = i ( r + i ) desde r = 1 hasta r = 3 R . Í ( 4 + l n 3 ) U
5. El a l d e t a espiral logarítm ica r = m > 0, ,u e se encuentra
dentro del círculo r - a.
R. a
N
1 + m z
-------- - u
m
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-279-320.jpg)


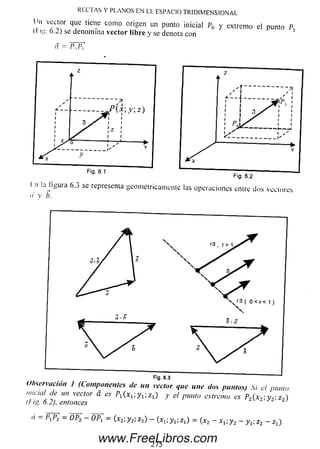


![TOPICOS DE CALCULO - VOLUMEN II
6.1.5.1 P R O P IE D A D E S
Sean á ,b y c vectores en el espacio R 3 y sea r un escalar. Entonces se tiene
1. á -b = b ■a (Propiedad Conm utativa)
2. ( r a) ■(b ) = r (a - b)
3. á - ( b ± c ) = d - b ± á - c (Propiedad Distributiva)
4. a •a = ||al|2 ; a ■a = 0 <=>á = 0
5. ||a+ ¿||2 = Hall2 + ||£||Z + 2a-b
6. ||a— b2 = Hall2 + ||fe||2 - 2a •5
7. ||a+ b||2 + ||a - fc||2 = 2[|a[|2 + 2||fo||2 (Ley del paralelogram o)
6.1.6 Á N G U L O S E N T R E D O S V E C T O R E S
Sean a y b vi
espacio R 3. E l ár
a y b es el ]
0 (0 < Q < n) del
partir de un m ism o
Teorem a 1 S i 6
vectores no nulos
entonces
á
eos 6 = —
Ha
D e m o stra ció n Ejercicio para el lector
Observación 2 D el teorema 1 se deduce que unaform a alternativa para calcular
el producto escalar de los vectores á y b es
a - b = l|a||||£|| eos 9
setores no nulos en el
igulo entre los vectores
menor ángulo positivo
lerminado por ambos al
origen com ún (Fig. 6.6)
es el ángulo entre dos
á y b del espacio R 3,
~b
y e / a
O(origen)
Fig. 6.6
2 7 8www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-285-320.jpg)

![TOPICOS DE CALCULO - VOLUMEN II
Ejem plo 5 Sean a ,b y c vectores en el espacio IR3 tales que ||a[| = 6.
p|| = 2 V 3 y ||c|| = 2. Sabiendo que los vectores a y b forman un ángulo de
30°, los vectores b y c un ángulo de 6QC y los vectores a y c un ángulo de
90°, calcule
a) a - ( b + c) b) ||a - c||
So lu ción Tenem os
a) á - ( b + c) = á - b + d - c = H a llp H eos 30° + ||a||||c]| eos 90°
= 6 ( 2 V 3 ) ^ ~ j + 6 (2 )( 0 ) = 18
b) ||a - c||2 = ||a||2 - 2 a •c + |lc|l2 = 36 - 2||a||l|c|| eos 90° + 4 = 40
D e donde se obtiene
||a - c|| = V 4 Ó
6.1.8 C O M P O N E N T E Y P R O Y E C C I Ó N O R T O G O N A L D E U N V E C T O R
E N L A D I R E C C I Ó N D E O T R O V E C T O R
Sean a y b vectores no nulos en el espacio K 3
A l vector OM (Fig. 6.8) se llama vector proyección orto go n al de a sobre b y
se denota com o
OM = P ro y ^ a
En el siguiente teorema verem os el procedimiento para determinar este vector
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-287-320.jpg)

![Eje m p lo 7 Sean a y b vectores en el espacio E 3 que verifican a + 3b = 0 y
c o m p ga = - 6 . Calcule el valor de A = 5 (3 a + 2b) • (3 a - 2b)
Solución
C om o a = - 3 b , entonces los vectores a y b tienen sentidos opuestos. Luego,
el ángulo que forman estos vectores es 9 = rr. Adem ás,
||a|l = 1I-35H = 3||b|| (1 )
Por otra parte, •
TOPICOS DE CALCULO - VOLUMEN II
á - b Ha|| b I eos ti
Compga = = ---------¡r^ --------= -||a|| - - 6 = * ||a|| - 6 (2 )
' W MI
Reem plazando (2) en (1) obtenemos ||5|| = 2
A h o ra bien, usando las propiedades del producto escalar resulta
A = 5 ( 3 a + 2b) •(3 a - 2b) = 5 (9||a|i2 - 4||b||2) = 5 [9 (3 6 ) - 4 (4 )]
= 1 5 4 0
E je m p lo 8 D ado el triángulo de vértices ¿4(5; 2; 3), B (8 ; 2 ; - 1 ) y C ( 3 ; 3 ; 5 )
a) Halle las componentes del vector Proy-^M N si se sabe que el vector MN es
paralelo al vector AC , donde M está sobre el lado AB, N sobre el lado BC y
MN = 18
b ) Calcule A = 5 ( AC ■üjg + - C o m p ^ ^ f l j
Solución
Sean los vectores AB = (3; 0; - 4 ) y AC = ( - 2 ; 1; 2)
a) C om o MN || ~AC, entonces P roy ^ M N = MN. Adem ás,
WÑ = kAC = fc( — 2; 1; 2) (fc > 0)
Por otra parte, |¡MW|| = V 9 k 2 = 3fc = 18 = > k = 6
Por consiguiente, P royjgM N = 6 ( — 2; 1; 2) = ( — 12; 6; 1 2)
b) A q u í tenemos
AB 1 N 3 ^ 4^
^ " p f ¡ “ 5 C 3 : 0 ; _ 4 ) " ( 5 ; ; 5
__ , ¿ f l - Z C - 6 - 8 14
ComPrcAB = = — 3— - - y
AC
Luego resulta
/__ , 3 ___a ( 14 1 4
A = 5 yAC • Ujg + - C o m p ^ y lñ J = 5 ( - y - y ) = - 2 8
282www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-289-320.jpg)












![RECTA S Y PLANOS EN EL ESPACIO TRIDIM ENSIONAL
(>.2 R E C T A E N E L E S P A C I O
6.2.1 Á N G U L O S , C O S E N O S Y N Ú M E R O S D I R E C T O R E S D E U N A
R E C T A
Definición 1 Sea L una recta en el
espacio M 3. Se llama conjunto de
ángulos directores de la recta L al
conjunto ordenado {a, p, y}, donde a,
¡i, y son *os ángulos que form a la recta
L con los rayos positivos de los ejes de
coordenadas x, y A z respectivamente
(Fig. 6.14)
Los ángulos directores toman valores
entre 0 o y 180°, es decir,
0 C < a , p , y , < 180°
Observación 7 El ángulo entre dos rectas que no se intersecan, se define como
el ángulo form ado por rectas que se intersecan y que, al mismo tiempo son
paralelas a las rectas dadas.
Si una recta no está orientada (con respecto al sentido que debe tomar) tiene dos
conjuntos de ángulos directores que son:
{ a , p, y ) y { 1 8 0 ° - a , 1 8 0 ° - / ? , 1 8 0 p - y }
En lo que sigue, las rectas serán consideradas sin orientación.
Definición 2 L o s cosenos de los ángulos directores de una recta se llaman
cosenos directores de la recta.
U na recta tiene dos conjuntos de cosenos directores.
(eos a, eos /? ,eos y } y { - e o s a , - e o s / ? , - e o s y }
O b se rv a c ió n 8 D o s rectas son paralelas si y solo sí tienen los m ism os cosenos
directores.
D e fin ición 3 U n conjunto [a; b; c] es llamado números directores si existe una
constante fe ^ 0 tal que
a = k eos a, b = kcosp, c = kcosy
295www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-302-320.jpg)













![Observación 13 Sea Q un plano cuya normal es N y L una recta cuyo vector
dirección es á , entonces se tiene
i) L Q < = $ N ± a < = * N ' á = 0 (Fig. 6.27)
ii) L ± Q « N II a (Fig. 6.28)
KtUIAS Y PLANOS EN EL ESPACIO TRIDIMENSIONAL
L
Ñi k
l ] /
Fig. 6.27 Fig. 6.28
iii) Si L Q => L n Q = <Ji ó L c Q
iv) L c Q =$ N 1 a y P0 e L => P0 6 Q (Fig. 6.29)
v) Si L # Q => L fl Q = / es un punto. (Fig. 6.30)
Ni k
/ J
h
Fig. 6.29 Fig 6.30
E je m p lo 32 Halle la ecuación del plano que contiene a la recta
L: P — (1; 2; 2) + t(0; 3; 1), t 6 M y el punto Q0(2; - 3 ; 8 ) ,
So lu ción
Sea N el vector norm al del plano Q que
contiene a la recta L y al punto Q0 , entonces
N 1 á = (0; 3; 1) A N I P0Q0 = (1; - 5 ; 6),
d o n d e P 0( l ; 2 ; 2 )
309
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-316-320.jpg)


![Sean v = P0Q0 = (2; — 3; — 2) y á = ( 1 ; — 3 ; — 5), donde P0(0 ;2 ;5 ).
Mmonccs la distancia del punto Q0 a la recta L es
||i; x ¿t|| _ V 8 1 + 64 + 9 _ 22
d = l|a|| V H
Ejem plo 34 Halle la ecuación del plano que pasa por la rectade intersección de
los planos x — y 4 - 2 z 4 - 4 = 0 , 2 x 4 - y 4 - 3 z — 9 = 0 y es paralelo ala recta
cuyos números directores son [1; 3; — 1]
Solución
La ecuación de la familia de planos que pasan por la intersección de los pianos
dados es
x —y 4- 2z 4- 4 + k(2x + y + 3z —9) = 0
« (1 + 2 k)x + ( k - 1) y + (2 4- 3 k) z + 4 - 9k = 0
Luego N = (1 4- 2 k; k — 1; 2 4- 3 k) es el vector normal de la familia. C om o el
plano es paralelo al vector a = (1; 3; — 1), entonces IV l a «
Ñ ■d = Q <=> 1 4- 2/c 4- 3/c — 3 — 2 — 3/c = 0 => k = 2
Por tanto, la ecuación del plano descrito es
5 x + y 4- 8 z — 14 = 0
Ejem plo 35 D adas las rectas Lr P — (1; 2; — 1) 4- t ( l; 3; 1), t € 1 y
L2: Q = (5; — 1; — 2) + s(2 ; — 1; 2 ),5 6 K
Halle las ecuaciones de dos planos paralelos
Q }' Qz de m odo que
¿i c Q y ¿2 c Qz
Solución
Sea N el vector norm al com ún de los planos
<2i Y Qz => Ñ ± a = (1; 3; 1) y
J V 1 ¿ = ( 2 ; - 1 ; 2 )
Fig. 6.31
Luego, yv II a x b = (7; 0; — 7)
Si utilizamos, el vector normal N — (1; 0; — 1) y el punto Px( 1; 2; — 1) E Lr
como punto de paso del plano, entonces la ecuación del plano que contiene a la
recta L x es
TOPICOS DI- CALCULO - VOLUMEN II
Qt : 1 0 - 1) 4- 0(y - 2) - í ( z + 1) = 0 <=> Qr: x - z - 2 = 0
3 1 2
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-319-320.jpg)






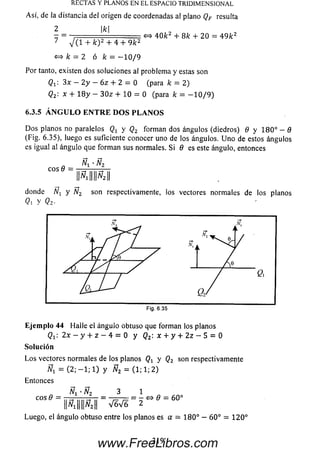

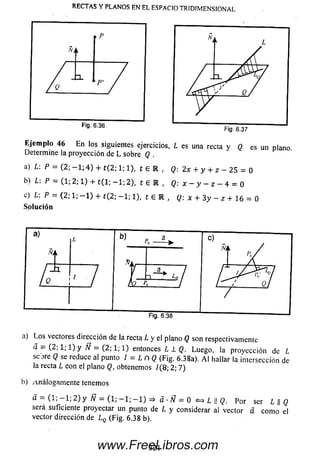

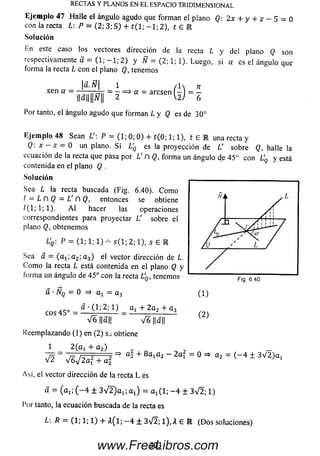

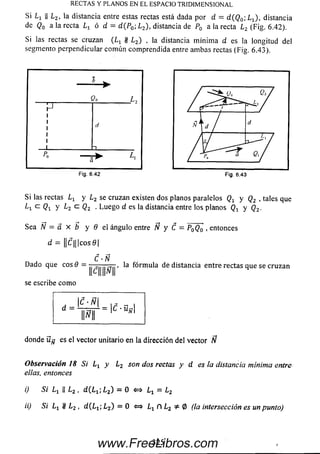



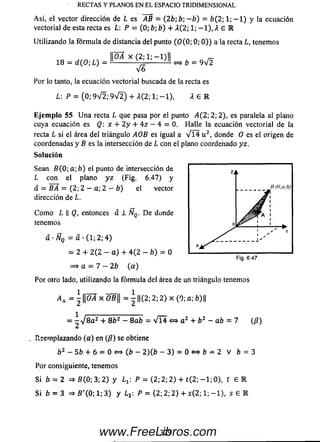



![RECTAS Y PLANOS EN EL ESPACIO TRIDIMENSIONAL
Sea I = n Q (en la Fig. 6.52, el plano Q se muestra de canto).
Luego,
/ (I + t; 4 + 2t; 3 - t) e Q e* 3(1 + t) - (4 + 2t) + 4(3 - t) = 2 <=> t = 3
= » /(4; 10; 0 )
Ahora, la ecuación vectorial de la recta que pasa por el punto P0 y sigue la
dirección del vector normal es LN: P = (1; 4; 3) + A(3; — 1; 4 ) ,X £ IR
Si M = Ln fl Q, entonces al hacer las operaciones respectivas obtenem os
/ 1 113 4 2
2 6 '" 2 6 " '2 6 /
Dado que Ai es el punto m edio del segmento P0Qo , entonces el punto Q0 es
/ 14 61 3
V 1 3 '1 3 '1 3 /
Por tanto, la ecuación vectorial del rayo reflejado que pasa por el punto I y sigue
la dirección del vector b = Q0I —— (66; 69; — 3) es
Lr : R = (4; 10; 0 ) + r (6 6 ; 69; - 3 ) , r £ IR
EJERCICIOS
1. Halle la ecuación de la recta que pasa por (1; 3; 2), es paralelo al plano
Q: P = (1; 4; 0 ) + r ( 1; 1; 1) + s ( 0; 1; 2), r, s £ E y form a un ángulo de
60° con la recta Lx R = (1; — 2; 3) + t(0; 1; 0), t £ E
R. L: = (1; 3; - 2 ) + t(3 ± 2V 2; 2 ± V 2; l) , t 6 E
2. Halle la ecuación del plano que pasa por (3; 1; — 2 ) y form a ángulos iguales
con las rectas Lx:P = (1; 4; 2) + t ( l; 1; 1), t £ E , ¿ 2; eíe x yL3: e ]e y
R. {x - 3) + (y - 1) + (V 3 - 2 )(z + 2) = 0
3. Sean las rectas:
Li'. P = ( 3 ; 0 ; 0 ) + t ( l; — 1; 1),t £ E
L2- Q — (2; 9;1) + s ( l ; 3; — í),s £ E
Halle la ecuación del plano que es paralelo a Lr y Lz, y divide en 2 partes
iguales al segmento de m enor longitud que une a dichas rectas.
4. Sea el plano con ecuación 2x + 3y + z + 4 = 0 , encontrar n y m no nulos de
m anera que los dos vectores A = i + j + k y B = nj + m k están en un
plano perpendicular al dado.
R . m = 1 / 2 , n = - 1 / 2
333www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-340-320.jpg)







![SUPERFICIES
U na superficie es un conjunto de puntos P ( x ; y ; z ) e R 3 cuyas coordenadas
satisfacen una ecuación dada en las variables x, y y z, esto es,
S — {(x; y ; z ) 6 E 3 / £ ( x ; x; z) = 0} es generalmente una superficie.
U n ejemplo de superficie es el plano (su ecuación es Ax + B y + Cz + D = 0)
Observación 1 Existen ecuaciones tales como
a) x 2 + ( y - 2 ) 2 + z 2 + 8 = 0
b) (x + l ) 2 + 4 (y - 2 ) 2 + 3(z - 5 ) 2 = 0
que no representan a una superficie. Para la ecuación (a), no existen números
reales x, y, z que satisfagan la ecuación dada, en este caso se dice que (a)
representa al conjunto vacío (0)
Para la ecuación (b), los únicos números reales que satisfacen la ecuación son
x = —1, y = 2, z = 5. Luego, la ecuación (b) representa solamente al punto
P C-l; 2; 5).
Observación 2 (Traslación de ejes) De modo similar a la traslación de ejes en el
plano cartesiano, se efectúa la traslación de ejes en el espacio tridimensional R 3.
Si el sistema de coordenadas o x yz se traslada a un nuevo origen 0 '(h ; k; l), de
modo que las coordenadas de cualquier 7 z
punto P E I 3 antes y después de la 11 ‘ 1
traslación son (x y z ) y ( x 1;y' ; z ' ) f|P
respectivamente (Fig. 7.1), entonces las ]
relaciones de tranformación del sistema " z -
original (oxyz) al nuevo sistema de ^ Y
coordenadas (o’x'y'z') son
x = h + x'
y = k + y'
■ z = l + z'
Fig. 7.1
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-348-320.jpg)









![i) C on planos paralelos al plano xy.
z = k => y 2 —4 y + 2k = 0 ==>y = 2 ± V 4 — 2k
Existe intersección para k < 2 (Para k = 2 es una recta, para k < 2
son dos rectas paralelas)
ii) C o n planos paralelos al plano xz. y = k => 2z - 4k - k 2, es una recta
V k e M
iii) C on planos paralelos al plano yz. x = A: => y 2 - 4 y + 2z = 0 , es una
parábola, V fc 6 IR
IV . Exte n sió n
L a ecuación y 2 - 4 y + 2z = 0 está definida V x 6 l (de I I I - iii),V y £ E
(de 111- ii) y V z 6 (— oo; 2] (de 111- ii).
V. Sim e tría s
Existe simetría con respecto al plano yz.
V I. G rá fica
En la Fig. 7.7 se muestra la parte de la superficie que se encuentra en el
primer octante. L a superficie se denom ina c ilin d ro parabólico.
E J E R C I C I O S
E n cada uno de los siguientes ejercicios efectúe la discusión y trace la gráfica de
la superficie representada por las ecuaciones dadas.
TOPICOS DE CALCULO - VOLUM EN II
lli. Trazas en lo s p la n o s p a ra le lo s a los p la n o s c o o rd e n a d o s
1. 4 x 2 + y 2 + z 2 = 4 (elipsoide)
2. x 2 + y 2 - z 2 - 0 (cono circular)
*»
4 . X 2 + z 2 - 4 y = 0 (Paraboloide de revolución o circular)
4, y 2 - x 3 = 0 (Cilindro)
5. 9 x 2 - 4y 2 - 4 z 2 = 36 (Hiperboloide circular de dos hojas)
6. 9 x 2 - 4y 2 + 4 z 2 = 36 (Hiperboloide elíptico de una hoja)
7. y 2 - x 2 = 2z (Paraboloide hiperbólico)
8. x 2 + y 2 + z 2 = 4 (esfera)
9. y 2 - x 2y = 0
10. z = |y|
351
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-358-320.jpg)

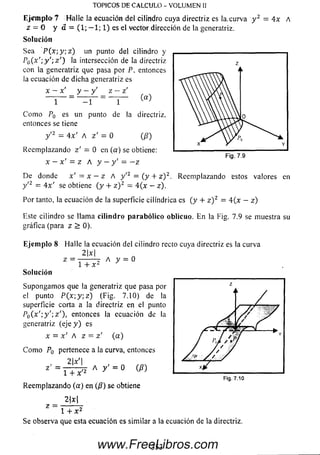

![Topiros nr r i m n - voi i'm fn u
E JE R C IC IO S
I. E n cada uno de los siguientes ejercicios halle la ecuación del cilindro usando
las ecuaciones de la directriz y el vector dirección de la generatriz.
1. x 2 + 4 y = 1 A z = 0 , a = (1; 1; 3)
R. 9 x 2 + z 2 - óxz - 3 6 y 4- 12z = 0
2. y 2 ~ z 2 = 1 A x = 0 , d = (-1 ; 1; 2)
3. x 2 + y = 1 A z = 0 , a = (2; 1;0)
II. Esboce la gráfica de la superficie representada por cada una de las siguientes
ecuaciones
1. y 2 —2 y + 4 = z
2. y = c o s x , x e [0; An]
3. y 3 = x 2
4. x 2 - y 2 = 1.
5. 4 x 2 + y 2 — 4
6. y = ln x
8. y 2 = 4 z
9. z = x e x
n n
1 0 .y = t a n z , z e < ~ 2 : 2^
3 5 5www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-362-320.jpg)
![SUPERFICIES
7.4 SU PE R FIC IE S DE R EV O LU C IÓ N
La superficie generada por la rotación de
una curva plana alrededor de una recta
fija que está en el plano de la curva, se
llama superficie de revolución. L a recta
fija se llama eje de revolución y la curva
plana se llama curva generadora.
Si por un punto cualquiera P (x ; y ;z ) se
traza un plano perpendicular al eje de
revolución, la intersección de la superficie
con dicho plano es una circunferencia
(Fig. 7.15).
Si C es el punto de intersección del plano con el eje de revolución L y Q es el
punto de intersección con la curva generadora, entonces se verifica
d{P-,C) = d (Q ,C )
A la ecuación generada por esta igualdad se denomina ecuación de la superficie
de revolución.
En lo que sigue, se considera que la curva generadora está contenida en un plano
coordenado o en un plano paralelo a un plano coordenado.
Observación 4 En la siguiente tabla, se muestra la forma de la ecuación de una
superficie de revolución generada por una curva que se encuentra en un plano
coordenado y gira sobre uno de los ejes coordenados.
Ecuación de la curva
generadora
Eje de
revolución
Ecuación de la superficie de
revolución
o
II
x
II
N
eje y x 2 + z 2 = [/ (y )]2
* = / ( y ) , z = o eje y x 2 + z 2 = [ f ( y ) ] 2
y- = / ( * ) , y = 0 eje x y 2 + z 2 — [ f{ x ) Y
y = f ( x ) , z = 0 eje x y 2 + z 2 — [/ (x )]2
y = / ( z ) , x = 0 e je z x 2 + y 2 = [/ (z )]2
x = A * ) . y = 0 e je z x 2 + V 2 = í f ( z ) ] 2
Fig. 7.15
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-363-320.jpg)
![TOPICOS DE CALCULO - VOLUM EN II
Dem ostrem os la prim era fórm ula de la
tabla, donde la ecuación de la curva
generadora es C: z = / (y ), x - 0 y el
eje de rotación es el eje y.
Sea P (x ;y ;z ) un punto cualquiera de la
superficie de revolución. Si Q es el punto
de intersección del plano perpendicular al
eje y que pasa por P con la curva
generadora y C es el punto de intersección
de dicho plano con el eje y, entonces
<2(0;y;/(y)) y c ( 0 ; y ; 0 )
Luego, de la definición de la superficie de revolución resulta
d(P; C) = D(Q; C) <=> J x 2 + z 2 = |/(y)| <=> x 2 + y 2 = [ f ( y ) ] 2
E n los otros casos, la dem ostración es similar.
Observación 5 Si el origen de coordenadas se traslada al punto O '( x 0;y 0; z0),
las ecuaciones de las superficies de revolución de la tabla anterior tienen las
siguientesformas:
i) (x - x0) 2 + (z - z 0) 2 = [/ (y - y 0) ] 2
¡O (y " yo)2+ (z - z0)2= [/(*- *0)]2
iii) (x - x 0) 2 + ( y - y 0) 2 = [/ (z - z0) ] 2
E je m p lo 10 E n cada uno de los siguientes ejercicios se da la ecuación de la
curva generadora y el eje de revolución L, determine la ecuación de la superficie
de revolución y esboce su gráfica.
a) C:z = ey , x = 0 ; L: eje y
b) C:z = e v, x = 0 ; L: eje z
c) C: z 2 - 4y 2 = 1, x = 0 ; L: eje y
2x
d)C : z = Y + x 2 ' y = 0 ' L: eJe x
e) C:y = x 2, z = 0 ; L: eje x
f) C:y - x 2, z = 0 ; L: eje y
So lu ció n
Fia. 7.16
357
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-364-320.jpg)

![Ejem plo 11 E n cada uno de los siguientes ejercicios se da la ecuación de la curva
generadora C y el eje de giro halle la ecuación de la superficie de revolución.
a) C: z = / (y ), x = a ; L z = b , x - a
b) C: z = 2 y - 3, x = 5 ; L: z = - 1 , x = 5
c) C: 4 (x + 2 ) 2 — ( y - l ) 2= 1, z - 3 ; L: eleje im aginario de la hipérbola
d) C: 4 ( x + 2 ) 2 — ( y — l ) 2= 1, z = 3 ; L: el eje transverso dela hipérbola
So lu ción
a) En la Fig. 7.23 se muestra la curva C y
la recta L en el plano x = a . Luego,
C(a; y: b), Q (a;y; / ( y ) ) y P ( x ; y ; z )
De la definición de la superficie de
revolución, tenemos
d(P; C) = d(Q-,C)
Por tanto, la ecuación de la superficie de
revolución es
(x - a ) 2 + (z - b Y = [/ (y ) - b]2
Esta ecuación también puede obtenerse
trasladando previamente el origen al
punto 0 '( a ; 0 ; ¿ ) .
b) (x — 5 ) 2 + (z + l ) 2 = ( 2 y — 2 ) 2 (cono de revolución o cono circular)
(y + 1 )2
c) (x + 2 )2 + (z —3 )2 -------- ------ = 1 (hiperboloide circular de una hoja)
4
d) (y + l ) 2 + (z - 3 ) 2 = 4 (x + 2 ) 2 - 1 ó
4 (x + 2 ) 2 — (y + l ) 2 — (z —3 ) 2 = 1 (hiperboloide circular de dos hojas)
Ejem plo 12 En cada uno de los siguientes ejercicios, identifique si es una
superficie de revolución. Luego, determine el eje de revolución y la ecuación de la
curva generadora.
a) x 2 = 5 + z 2 —y 2
b) 2 x 2 + 4 z 2 + y 2 = 1
c) x 2 + 2 y 2 4- 2 z 2 — 4 x 4- 8 y — 4 z — 4 = 0
d) 2 x 2 4 2 z 2 4 4 x 4 y - 4 z 4 - 4 - 0
Solución
SU PERFICIES
360www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-367-320.jpg)
![lU l'IL U ^ U t L A IX U L U - VO LU M bN H
a) x 2 + y 2 = 5 + z 2 (hiperboloide circular de una Jioja)
i) Eje de revolución L: x - 0, y — 0 (ejez)
ii) C u rva generadora C: x = 0, y = v 5 -f z 2 ó y = 0 , x = V 5 + z 2
(hipérbola)
b) N o es una superficie de revolución (ninguna de las trazas en los planos
paralelos a los planos coordenados es una circunferencia).
(x — 2)2
c) (x + 2 ) 2 + (z - l ) 2 = 9 --------------- (e lipso id e de re volu ció n o esferoide)
i) Eje de revolución L: x = —2 , z = 1
18 - (x - 2) 2
ii) Curva generadora C: x = —2, z - 1 +
N
d) (x + l ) 2 + (z - l ) 2 = - 1 (paraboloide circu lar)
(elipse)
i) Eje de revolución L: x - — 1, z = 1
y¡~2
ii) Curva generadora C:x = —1, z = l + (parábola)
7.5 S U P E R F I C I E S C U A D R A T I C A S
U na superficie cu ad rática o simplemente cuád rica es la gráfica de una ecuación
de segundo grado en las variables x ,y ,z .
A lgu n as superficies cilindricas o superficies de revolución son ejemplos de
cuádricas. En ésta sección se presentará algunas form as usuales de las superficies
cuadráticas cuyas ecuaciones están en su form a m ás sim ple (form a canónica).
Considerando que el lector está en condiciones de discutir la ecuación de una
superficie, nos lim itarem os a describir algunas propiedades de estas superficies.
7.5.1 E L I P S O I D E
L a form a canónica de la ecuación del elipsoide con centro en el origen es
x 2 y 2 z 2
a2 ^ b 2 + ^2 = 1
donde a, b y c son núm eros reales positivos. Adem ás, los intervalos de variación
de las variables x, y a z son
x £ [ - a ; a], y 6 [ - b ; b] A z e [ - c ; c]
361
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-368-320.jpg)

![Los intervalos de variación de las variables x, y A z son
x 6 ( - 00; - a ] U [a; + 00), y e (— 00; - b] U [fe; + 00) y z £ < - 00; + 00)
Si a 2 = b 2, es una superficie de revolución (hiperboloide circular de una hoja)
Si a 2 & b 2, la superficie es el hiperboloide elíptico de una hoja, las trazas en
los planos paralelos al plano x y son elipses o circunferencias según sea el caso en
que
a 2 b 2 ó a 2 = b 2
Las trazas en los planos paralelos a los planos x z e yz son hipérbolas, (en los
planos y - b , x - a son dos rectas que se cortan).
Esta superficie es simétrica con respecto a los ejes coordenados, a los planos
coordenados y al origen de coordenadas.
La forma ordinaria de la ecuación del hiperboloide de una hoja con centro en el
punto C(h) k; l) es
(x - h) 2 (y - k)2 (z - O 2
a2 b2 c2 1
7.5.3 H IP E R B O L O ID E E L ÍP T IC O ( C IR C U L A R ) D E D O S H O J A S
La forma canónica de la ecuación del hiperboloide de dos hojas con centro en el
origen es
x 2 y 2 z 2 ( x 2 y 2 z 2 , x 2 y 2 z 2
~ a 2 + b 2 ~ 7 2 = 1 ° ^ 2 ~ b 2 ~ c 2 = 1 ° ~ á 2 ~ b 2 + c 2
donde a, b y c son números reales positivos.
En la Fig. 7.26 se muestra la gráfica de
x 2 y 2 z 2
~~¿2 + ¥ ~ c 2 = 1
Los intervalos de variación de las
variables x ,y A z para esta
superficie son
x £ ( - 00; + 00),
y £ (— 00; -b] U [b; +co) y
Z £ ( - 00; +«>)
TOPICOS DE CALCULO - VOLUM EN II
A continuación se describe algunas propiedades de esta superficie
363www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-370-320.jpg)

![TO PICO S DE C A L C U L O - V O L U M E N II
S i c < 0 el paraboloide se abre hacia la
parte negativa del eje z.
Los intervalos de variación de las variables
x, y A z para la ecuación de esta
superficie son:
x £ (— c°; + c o ), y 6 ( —00; + 0 0 ) y
z £ [0; + 0 0 ) (s i c < 0, z £ (-0 0 ; 0])
Si a 2 = b 2 , la superficie es una superficie
de revolución (p arabo loid e circu lar)
Si a 2 & b 2, la superficie es el paraboloide
elíptico.
Las trazas en los planos paralelos al plano x y son circunferencias o elipses según
sea el caso en que a 2 = b 2 ó a 2 * b 2. (En el plano z = 0. la traza es un
punto).
Esta superficie es simétrica con respecto al eje z, al plano ‘xz y al plano yz.
La form a ordinaria de la ecuación del paraboloide con vértice en el punto
V (h ,k ;l) es
(x - h.)2 (y - k ) 2
= c (z - i)
a 2 b 2
En los otros casos, la ecuación es de la forma
{ x - h ) 2 ( z - l ) 2
■H----------- b (y - k) ó
(y - k ) 2 ( z - 0
+ ■ = a(x - h)
7.5.5 P A R A B O L O I D E H I P E R B Ó L I C O ( S I L L A D E M O N T A R )
La form a canónica de la ecuación del paraboloide hiperbólico con punto de silla
en el origen de coordenadas es
y -
b 2
x c
a2
cz
í z 2 x 1
ó — - — = by , ó
V, cL a 2
z 2 y 2
c ‘ b 2 )
donde a y b son núm eros positivos y c i d ,
En la Fig. 7.28 se muestra la gráfica de
y 2 x 2
- r r ------- - CZ , con C > 0
o 2 a 2
L o s intervalos de variación para las variables x ,y A / de esta superficie son
X £ (-0 0 , + 0 0 ), y 6 (- 0 0 , + 0 0 ) V Z £ (-0 0 , + 0 0 )
365www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-372-320.jpg)




![i) Encuentre las coordenadas cartesianas del punto que tiene las coordenadas
cilindricas dadas
3) ( 3 ; f ; 5 j b) ( 7 ; y : - £ ) c) (1; 0; 1)
ii) Encuentre un conjunto de coordenadas cilindricas del punto cuyas
coordenadas cartesianas son
a) (4; 4 ; - 2 ) b) ( - 3 V 3 ; 3; 6) c) (1; 1; 1)
Solución
i) a) Si las coordenadas cilindricas de P son (3; n /2 ;5 ), entonces r = 3.
0 - n /2 y z = 5. Luego, aplicando las fórm ulas que relacionas estas
coordenadas con las cartesianas se tiene
x = 3 cos(7r/2) = 0, y = 3 se n (n /2 ) = 3 y z = 5
Por tanto, las coordenadas cartesianas de P son (0 ; 3 ; 5)
Procediendo de manera similar se obtiene
u- í 7
— ; - 4 c) (1;0; 1)
V^ *-¡
ii) a) Si las coordenadas cartesianas de P son (4; 4 ; - 2 ) . entcnces x = 4,
y - 4 y z = 5
Luego, aplicando las fórm ulas que relacionas estas coordenadas con las
cilindricas tiene
y 4 n
tan 0 = - = - = 1 => 6 = - , r ‘ = x 2 + y 2 = 32 => r = 4 V 2 , z = 5
X i 4
Por tanto, las coordenadas cilindricas de P son (4 V 2 ; 7r/4 ; 5)
b) (6 ; 5n/6 ; 6) c) (V 2 ; n/4] l )
Ejem plo 16 Halle una ecuación en coordenadas cilindricas para la superficie
representada por la ecuación cartesiana
a) 2x -f y — z = 0 b) x 2 + y 2 = 4z
c) x z - y 2 - 4 z z - 4 = 0 •
Solución
Reem plazando x = r eos 0, y = r sen G y z = z, se obtiene
a) 2 r eos 6 + r sen 9 - z = 0
b) r2 - 4z
c) r2 eos 2 0 - 4 z 2 - 4 = 0
s u p e r f i c i e s
rjc m p io 15
370www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-377-320.jpg)


![5. Halle una ecuación en coordenadas cilindricas de la superficie cuya ecuación
en coordenadas cartesianas es
TOPICOS DE CALCULO - VOLUM EN II
6. Las siguientes superficies están descritas en coordenadas esféricas. Encuentre
sus ecuaciones rectangulares.
7. H alle una ecuación en coordenadas esféricas, para la esfera de radio 3 con
centro en (0; 1; 0)
8. Halle una ecuación en coordenadas cilindricas para la esfera del ejercicio 7.
9. En los siguientes ejercicios, encuentre las ecuaciones en coordenada
cilindricas y en coordenadas esféricas para la superficie dada.
a) E l paraboloide x 2 + y 2 = 4 z b) E l hiperboloide x y = z
10. Describir la superficie z = 2 r (coordenadas cilindricas), y obtener una
ecuación de la m ism a en coordenadas cartesianas.
11. H alle una ecuación en coordenadas rectangulares(cartesianas) de la superficie
a) (x + y ) 2 = z —5 b) x 2z 2 = 25 — y 2z 2
d) ax + b y + cz = x 2 + y 2 + z 2
a) cot 0 = sen 8 + eos 6
c) p = a sen 0 sen 8 d)
b) p 2 eos 2 0 = a 2
p 2 se n 20 sen 28 = a 2
z 2 = i _ (r _ 2 ) 2
7.7 A P L I C A C I O N E S
E je m p lo 17 Calcule el volum en del sólido limitado por la superficie z = x 2 + y 2
y el plano z = 4
So lu ció n _________________________________
L a ecuación z = x 2 + y 2 representa un
paraboloide circular. Las secciones
transversales perpendiculares al eje z son
círculos de radio r = V i (Fig. 7.35).
E l área de cada sección transversal es
A (z) = n z , z G [0; 4]
Y
Por consiguiente, el volum en del sólido es
x
Fig. 7.35
= 8nu3
373www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-380-320.jpg)
![SUPERFICIES
Ejem plo 19 ¿L a ecuación x 2 + y 2 - e 2z = 0 representa una superficie de
revolución? Ln caso afirmativo, halle el área de la superficie com prendida entre
los planos z — 0 y z = 1 y calcule la longitud de arco de la curva generadora.
Solución
x 2 + y 2 = e 2z representa una superficie de revolución. E l eje de revolución es el
eje z, ( x - 0 , y = 0) y una curva generadora es C: y = e z, x = 0
Para determinar el área de la superficie de revolución com prendida entre los
planos z — 0 y z = 1 (Fig. 7.36), basta considerar el arco de la curva y — e z .
z e [0; 1] en el plano x = 0 y hacerla girar alrededor del eje z. (Fig. 7.37)
i
N
II
0 1 ” z
Fig. 7.36
Luego, el área de esta superficie de revolución es
Fig. 7.37
^~lyJ1+[§]iz*ievl+e”‘¡z
e V 1 + e 2 + ln |
/T~,;—7 i /e + Vi + e2
= - e V 1 + e 2 + ln ------------— —
2 V 1+V2
La longitud de arco de la curva generadora resulta
- V 2
Haciendo la sustitución trigonométrica e z = tan 0 <=* z = ln (ta n 0 ), obtenemos
-arctan e ^ ¿-arctane
------ r ------
sen 0 e os2#
4 4
/•arctan e
- I (ese 9 + tan 9 sec 9) d9
ln
Vi + 1
- ln(V2 - l) + V i + e2 - V 2
374www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-381-320.jpg)
![TOPICOS DE CALCULO - VOLUMEN II
E je m p lo 20 Calcule el volum en del sólido limitado por las superficies
9 x 2 — 9y 2 + 4 z 2 — 36x — 8z 4- 4 = 0. y = — 1 A y = 4
So lu ción
A l completar cuadrados en la ecuación de la
superficie se obtiene
( * 2 ) 2 + ( z - l ) 2
4 9
Asi. la superficie es un hiperboloide elíptico
de una hoja cuyo centro es C ( 2 ; 0 ; l) .
La gráfica del sólido se muestra en la Fig.
7.38. Las secciones transversales del sólido
perpendiculares al eje y son las elipses
(.x - 2 )z (z - l ) 2
■ ■ - t - —— — — —
4
(x - 2 )2
4 1
■4- ■
9
(z - l ) 2
9 1
= 1 + :
1, donde t =
4 4- y 2
Luego, el área de la elipse (sección transversal) es
/4 4- y 2
A (y) = ír ( 2 V t ) ( 3 V t ) = 6 n :(— - — y 6 [ - 1 : 4 ]
Usando el método de secciones transversales, el volum en del sólido es
- 4 3 r4
j A (y ) d y = - n J (4 + y 2) d y =
Eje m plo 21 Calcule el volum en del sólido limitado por la superficie
y 2 4- z 2 - 2 se n 2* - 2 sen * - c o s2x = 0 y los planos x = 0 y x = n /2 .
So lu ción
L a ecuación se puede escribir com o y 2 + z 2 = ( s e n x 4- l ) 2. Esta ecuación
representa una superficie de revolución cuyo eje de giro es el eje x.
L a sección transversal del sólido perpendicular al eje x es el circulo
y 2 4- z 2 = (sen x + l ) 2, x £ jo;-]
A sí, el área de la sección transversal es
A (x) = 7r(señx 4-1)2. x e [0 ;-|
Por consiguiente, el volum en del sólido resulta
f n/z f 1 , ít(37t 4- 8)
V(S) = I A{x)dx ~ n (sen x 4-1)2 dx = -------
jo 'o
u
375
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-382-320.jpg)
![SUPERFICIES
Ejem plo 22 C a lc u le el v o lu m e n d e l s ó lid o lim ita d o p o r las s u p e rfic ie s
o - x , y2Z — —— b ——
4 9
y —
* 4
= z 2
Solución
x y
La ecuación 2z = — + — representa
representa a un paraboloide con vértice
en el origen y la ecuación
„2 ,,2
representa a un cono con
x . y 2
T + T = z
representa a un cono con vértice en el
origen.
Estas superficies se intersecan cuando
L a sección transversal del sólido,
perpendicular al eje z, es el anillo
elíptico cuya área es
A (z) = 7 r ( V 8 z ) ( V l8 z ) - n ( J a z 2) ( V 9 ? ) = I2 n z - 6 n z 2,z 6 [0; 2]
Por lo tanto, el volum en del sólido es
y ( S ) = í (127TZ —6 n z 2)d z = 8n u 3
■>o
E je m p lo 23 U n sólido está limitado por las superficies
1
S i: p = - cot <pese (p (en coordenadas esféricas)
S2: z = 3 (en coordenadas cilindricas)
Bosqueje la gráfica y calcule el volum en
del sólido.
So lu ción
Utilizando las relaciones entre las
coordenadas esféricas y las coordenadas
cartesianas: z — p eos (p,
y = p sen (p sen 0. x = p sen (p cos:0 se
tiene x z + y 2 = p 2 se n 2(p.
3 7 6www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-383-320.jpg)
![De la ecuación de resulta
cosrf) -, -, , ,,
3 p = ----- r—- <=> 3p 2 se n 2<p = p eos cp => 3 0 " + y ) = z
sen¿q)
Esta ecuación representa a un paraboloide circular.
Por otro lado, la ecuación cartesiana de S2 es z = 3.
L a gráfica del sólido se muestra en la Fig. 7.40. La s secciones transversales del
sólido, perpendiculares al eje z, son círculos de radio r = *Jz~/3. A sí, el área de
la sección plana es
A (z) = y , z 6 [0; 3]
U sando el método de secciones planas, el volum en del sólido resulta
f 3 nz 3n ,
n s ) = Jj T * = y U
Eje m p lo 24 Halle la ecuación de la recta que pasa por el punto Pt (0; - 2 ; 4 ) y
es tangente al cilindro 5: 2 y = x 2 . El ángulo que form a dicha recta con el plano
x y es de 30° (4 soluciones).
So lu ción
Sea P0(a; b; c) el punto de tangencia (Fig. 7.41 izquierda). En la vista horizontal
(visto desde arriba hacia abajo - Fig. 7.41 derecha), se tiene
TO PICO S D E C A L C U L O - V O L U M E N II
y + 2
Pendiente de la tangente: m = (a )
dy y + 2
Tam bién m = — = x. Luego, --------= x (p )
dx x
377
www.FreeLibros.com](https://image.slidesharecdn.com/tpicosdeclculovol-160920060041/85/Topicos-de-calculo-volumen-II-MAXIMO-MITACC-384-320.jpg)

