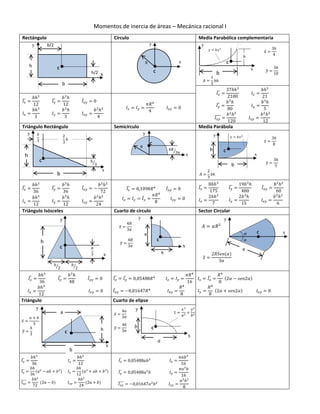
Este documento presenta fórmulas para calcular momentos de inercia de diferentes áreas geométricas como rectángulos, círculos, triángulos y elipses con respecto a ejes normales y oblicuos. También explica cómo rotar coordenadas y momentos de inercia para cambiar de sistema de ejes, y cómo encontrar los ejes principales de inercia que maximizan o minimizan el momento de inercia de una sección.

1. Momentos de inercia de áreas – Mecánica racional I
Rectángulo Círculo Media Parabólica complementaria
̅
̅
̅̅̅̅
̅ ̅ ̅
Triángulo Rectángulo Semicírculo Media Parábola
̅ ̅ ̅ ̅ ̅
̅
̅ ̅ ̅
Triángulo Isósceles Cuarto de círculo Sector Circular
̅ ̅ ̅ ̅ ̅
̅
̅ ( )
( )
Triángulo Cuarto de elipse
̅
̅ ( ) ( )
̅̅̅̅ ( ) ( )
̅
̅
̅̅̅̅
b
h
y b/2
h/2 x
R
y
x
x
y
𝑦 𝑘𝑥
h
b
C
𝑏
𝑏
C
y
x
b
h x
𝑅
𝜋
R
C
y
𝑥̅
𝑏
𝑦̅
b
h
𝑥̅
𝑏
𝑦̅
x
y
h
𝑏 𝑏
y
x
C
C
C
C
R
R
y
x
𝑥̅
𝑅
𝜋
𝑦̅
𝑅
𝜋
C
𝛼
𝛼
C
y
x
𝑥̅
𝑅𝑆𝑒𝑛(𝛼)
𝛼
𝑦 𝑘𝑥
hC
y
x
b
a
𝑥̅
𝑎 𝑏
𝑦̅
𝑥
𝑎
𝑦
𝑏
𝑎
𝑏
𝑥̅
𝑎
𝜋
𝑦̅
𝑏
𝜋
x
y
C
𝐴 𝑏
𝐴 𝑏
𝐴 𝛼𝑅

2. Ecuaciones: Momento de inercia para un área con respecto a ejes inclinados
Transformación de coordenadas: Conocidas las coordenadas de un punto
respecto a un sistema de coordenadas y el ángulo de rotación se
puede hallar los valores de coordenadas del mismo punto respecto a otro
sistema de coordenadas .
.
{
( ) ( )
( ) ( )
Rotación de momentos: Si se conoce el momento de inercia y producto de inercia respecto de ciertos ejes
se puede determinar el momento de inercia y producto de inercia para ciertos ejes conociendo el ángulo
de rotación .
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
.
Momento máximo y mínimo: Los llamados ejes principales de inercia son los ejes para los cuales el momento de
inercia es máximo o mínimo en una sección dada, estos ejes se encuentran a cierta inclinación respecto a los
ejes normales, en general hay un conjunto de ejes principales para cada origen O elegido. Para el diseño
estructural de un miembro el origen se coloca generalmente en el Centroide de la sección transversal.
( ) ( )
( )
( )
√( )
√( )