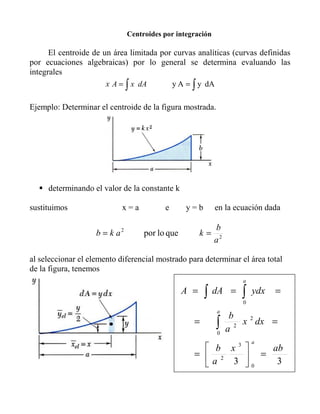
Este documento describe cómo calcular el centroide de un área limitada por curvas analíticas integrando las expresiones para el primer momento del área con respecto a los ejes x e y. Proporciona un ejemplo de determinar el centroide de una figura definida por la ecuación k=a2b2. Calcula los primeros momentos integrando un elemento diferencial horizontal y concluye dando las coordenadas del centroide.

1. Centroides por integración
El centroide de un área limitada por curvas analíticas (curvas definidas
por ecuaciones algebraicas) por lo general se determina evaluando las
integrales
∫ ∫== dAyAydAxAx
Ejemplo: Determinar el centroide de la figura mostrada.
determinando el valor de la constante k
sustituimos x = a e y = b en la ecuación dada
2
2
quelopor
a
b
kakb ==
al seleccionar el elemento diferencial mostrado para determinar el área total
de la figura, tenemos
33 0
3
2
0
2
2
0
abx
a
b
dxx
a
b
ydxdAA
a
a
a
=





=
==
===
∫
∫ ∫

2. dAxel es el primer momento del elemento diferencial con respecto al eje y
.
Por lo tanto el primer momento de toda el área con respecto al eje y
44
2
0
4
2
0
2
2
0
bax
a
b
dxx
a
b
xydxxdAxQ
aaa
ely =





=





=== ∫∫∫
como AxQy = tenemos ∫= dAxAx el por lo que
ax
baab
x
4
3
43
2
=⇒=





de la mismo modo, e primer momento del elemento diferencial con respecto
al eje x es dAyel y el primer momento de toda el área es
10522
1
2
2
0
5
4
2
0
2
2
2
0
abx
a
b
dxx
a
b
ydx
y
dAyQ
aaa
elx =





=





=== ∫∫∫
como AyQx = tenemos ∫= dAyAy el por lo que
by
abab
y
10
3
103
2
=⇒=





Tarea: Resuelva el problema, determinando un elemento diferencial
horizontal. ¿Qué concluye?