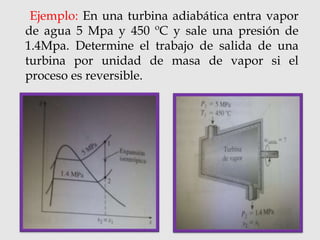
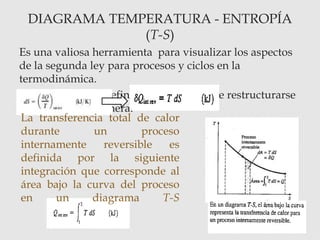
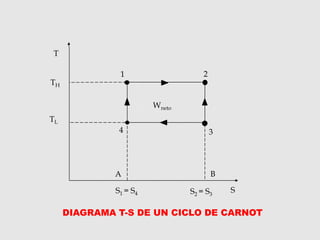
Este documento presenta información sobre procesos isentrópicos en los que la entropía se mantiene constante (Δs = 0). Incluye un ejemplo numérico para calcular el trabajo de salida de una turbina de vapor. También describe diagramas T-S y cómo se usan para analizar procesos termodinámicos, incluido el ciclo de Carnot.

1. UNIVERSIDAD SEÑOR DE SIPAN
FACULTAD DE INGENIERIA, ARQUITECTURA Y
URBANISMO
Escuela de Ingeniería Mecánica Eléctrica
Curso: Termodinámica
Tema: La Entropía
Docente: Cesar Manuel Sánchez Castro
Ciclo: IV
Integrantes:
• Víctor B. Valencia Manayay
• Miguel Incio Chapoñan
• Cesar Torres Lluen
• Walter Quiroz Montalvo
PIMENTEL – JUNIO 2015

2. Procesos Isentrópicos
Son aquellos procesos en el que la
entropía se mantiene constante y se
caracteriza por:
∆𝑠 = 0 ó 𝑠2 = 𝑠1 (𝐾𝑗/𝐾𝑔.K)
 Es decir, una sustancia tendrá el
mismo valor de entropía tanto al
final del proceso, como al inicio
del mismo, si el proceso se lleva a
cabo de una manera isentrópica.

3.  Por lo tanto la entropía de una
masa fija, no cambia durante un
proceso que es internamente
reversible y adiabático
 La entropía de una masa fija puede
cambiarse por:
 Transferencia de calor.
 Las irreversibilidades.

4. Un proceso adiabático reversible
necesariamente es isentrópico, pero un
proceso isentrópico no es necesariamente un
proceso adiabático reversible.

5. Ejemplo: En una turbina adiabática entra vapor
de agua 5 Mpa y 450 ºC y sale una presión de
1.4Mpa. Determine el trabajo de salida de una
turbina por unidad de masa de vapor si el
proceso es reversible.

6. 𝐸𝑒𝑛𝑡𝑟𝑎 − 𝐸𝑠𝑎𝑙𝑒 = ∆𝐸𝑠𝑖𝑠𝑡𝑒𝑚𝑎 /𝑑𝑡 = 0
𝐸𝑒𝑛𝑡𝑟𝑎 = 𝐸𝑠𝑎𝑙𝑒
𝑾 𝒇𝒍𝒖𝒋𝒐𝟏 + 𝑼𝟏 + 𝑬𝒄𝟏 + 𝑬𝒑𝟏 = 𝑾 𝒇𝒍𝒖𝒋𝒐𝟐 + 𝑼𝟐 + 𝑬𝒄𝟐 + 𝑬𝒑𝟐 + 𝑾 𝒔𝒂𝒍𝒊𝒅𝒂
𝐻1 = 𝐻2 + 𝑊𝑠𝑎𝑙𝑖𝑑𝑎 (𝐾𝐽/Kg)
ℎ1 = ℎ2 + 𝑊𝑠𝑎𝑙𝑖𝑑𝑎 (𝐾𝐽/𝐾𝑔)
𝑊𝑠𝑎𝑙𝑖𝑑𝑎 = 𝑚(h1 − h2)

7. vapor sobrecalentado
Estado 1 : P1=5Mpa h1=3316.1 𝐾𝐽/𝐾𝑔
T1=450ºC s1=6.8186
𝐾𝐽
𝐾𝑔
∗ 𝐾
Estado 2 : P1=1.4Mpa
s1=s2 vapor sobrecalentado
2927.2 ⟶ 6.7467
h2 ⟶ 6.8186
3040.4 ⟶ 6.9533
h2 =3040.4-
6.9533−6.8186
6.9533−6.7467
× 3040.4 − 2927.2
h2 =2966.6 𝐾𝐽/𝐾𝑔

8. Entonces el trabajo de salida de la turbina por
unidad de masa de vapor de agua se estima en:
𝑊𝑠𝑎𝑙𝑖𝑑𝑎 = h1 − h2
𝑊𝑠𝑎𝑙𝑖𝑑𝑎 = 3316.1𝐾𝐽/𝐾𝑔 − 2966.6 𝐾𝐽/𝐾𝑔
𝑊𝑠𝑎𝑙𝑖𝑑𝑎 = 349.5 𝐾𝐽/𝐾𝑔

9. Los diagramas de propiedades proporcionan gran ayuda
visual en el análisis termodinámico de los procesos.
Los diagramas P-V y T-V se usan exclusivamente con la
primera ley de la termodinámica.
Para el análisis de la segunda ley es muy útil trazar los
procesos en diagramas en los que una de las coordenadas
es la entropía. Los diagramas normalmente usados en este
tipo de análisis solo la diagramas de temperatura-entropía y
entalpia-entropía.

10. DIAGRAMA TEMPERATURA - ENTROPÍA
(T-S)
Es una valiosa herramienta para visualizar los aspectos
de la segunda ley para procesos y ciclos en la
termodinámica.
La ecuación que define la entropía puede restructurarse
de la siguiente manera:
La transferencia total de calor
durante un proceso
internamente reversible es
definida por la siguiente
integración que corresponde al
área bajo la curva del proceso
en un diagrama T-S

11. Para resolver la integral de la ecuación se necesita saber
la relación entre T y S durante el proceso. Se puede
solucionar fácilmente en el proceso isométrico
internamente reversible.
Expresado en unidad de masa
- Donde:
o es la temperatura constante
o es el cambio de entropía del sistema durante el proceso

12. Diagrama T-S de proceso isentrópico
Un proceso isentrópico en un diagrama T-S, se reconoce
fácilmente como un segmento de línea vertical, porque
un proceso de este tipo no incluye transferencia de calor
y por consiguiente el área bajo la trayectoria del proceso
debe ser cero.

13. T
TH
TL
S1 = S4 SS2 = S3
A B
1 2
4 3
DIAGRAMA T-S DE UN CICLO DE CARNOT
Wneto

14. DIAGRAMA T-S DEL CICLO DE CARNOT
El ciclo de Carnot esta formado por dos procesos
isotérmicos reversibles (T = constante) y otros dos
isentrópicos (s = constante); los cuatro forman un
rectángulo, en un diagrama T-S, como se muestra en la
figura anterior.
En un diagrama T-S el área bajo la curva del proceso
representa la transferencia de calor para ese proceso,
por lo tanto el área A12B representa QH, el área A43B
representa QL y la diferencia entre ambas (área
sombreada) representa el trabajo neto porque:
Wneto de salida = QH – QL

15. DIAGRAMA T-S DEL CICLO DE CARNOT
Así, el área encerrada por la trayectoria de un ciclo
(área 1234) en un diagrama T-S representa el trabajo
neto.
Recuerde que esta misma área también representa el
trabajo neto sobre un diagrama P-V.

16. Es una propiedad de la Termodinámica que mide
el desorden o aleatoriedad molecular, cuando un
cuerpo o sistema, absorbe calor manteniendo su
temperatura y el desorden molecular de un
sistema aislado, aumenta siempre que
experimenta un proceso.
La entropía de una sustancia es mas baja en su
fase solidad y es mas alta en su fase gaseosa.

17. Probabilidad Termodinámica:
Es la relación de la entropía con el número de
posibles estados microscópicos o
configuraciones moleculares; que tiene un
estado en equilibrio macroscópico.
Y se expresa mediante la Relación Boltzmann
como:
S = klnp
Donde:
k = 1.3806 x 10 -23 J/K (Const. De Boltzmann)
P = Número de micro estados
Ln = Logaritmo natural

18. Tercera ley de la termodinámica:
“La entropía de una sustancia pura
cristalina, a una temperatura absoluta de
cero es cero”.
CRISTAL PURO
T = 0 K
ENTROPIA = 0
Entropía Absoluta:
Es la entropía determinada como relativa con
respecto a la tercera ley de la termodinámica.

19. Cuando hay transferencia de calor de un
cuerpo caliente a un cuerpo frio, se tiene que el nivel
de desorden molecular o aleatoriedad del cuerpo
caliente disminuyen con la entropía, mientras que el
nivel del desorden molecular del cuerpo frio aumenta,
la segunda ley de la termodinámica requiere que el
incremento en la entropía del cuerpo frio sea mayor
que la disminución en la entropía del cuerpo caliente,
“No hay transferencia de entropía,
asociada con la transferencia de energía
como trabajo”.
Por consiguiente, en la ausencia de cualquier
tipo de fricción, el proceso de levantar un peso
mediante un eje rotatorio no produce entropía.

20. por lo tanto la entropía neta del sistema combinado
(Cuerpos frio y caliente), aumenta.
Es decir, el sistema combinado se halla en un estado
de mayor desorden en el estado final.
Se puede concluir entonces, que el proceso sólo
puede ocurrir en la dirección del aumento de entropía
global o desorden molecular.

21. Dado el papel fundamental que desempeña la entropía en
la termodinámica, se justifica asignarle su propia unidad.
H.L. CALLENDAR (Proc. Phys. Soc. (London) 23 (1911)
173) sugirió, en honor a S. CARNOT, llamarla “Carnot”
abreviada como Ct = J/K. A partir de su trabajo en el campo
de máquinas termícas, el ingeniero francés Nicolas
Léonard Sadi CARNOT (1796-1832) realizó importantes
aportes al desarrollo de la termodinámica.

22. La Entropía y la generación de entropía en
la vida diaria
Las personas eficientes llevan vidas de baja entropía,
(son organizadas), tienen un lugar para toda cosa
(incertidumbre mínima) y emplean la menor energía
para localizar algo.
Por otro lado, las personas ineficientes llevan vida de
alta entropía: les toma minutos (si no son horas)
encontrar algo que necesitan, y es probable que creen
un desorden más grande mientras buscan, puesto
que probablemente dirigirán su búsqueda de una
manera desordenada.
Las personas que llevan estilos de vida de alta
entropía siempre están apuradas y nunca parecen
ponerse al día.

23. La Entropía y la generación de entropía en
la vida diaria
La fricción mecánica siempre esta acompañada por la
generación de entropía, por lo tanto el desempeño se
reduce; comparado en la vida cotidiana: la fricción en
el lugar de trabajo, con los compañeros, genera
entropía y por lo tanto afecta en forma adversa el
desempeño laboral, lo que resulta en una
productividad reducida.

24. VIDEO SOBRE LA ENTROPIA

25. MUCHAS GRACIAS
POR SU
ATENCIÓN