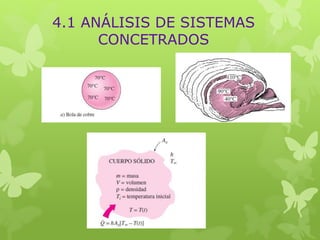
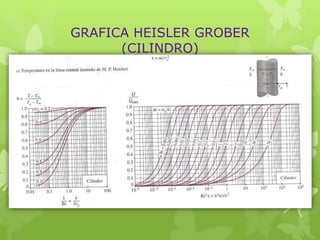
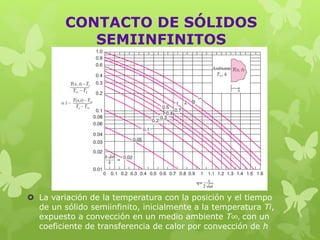
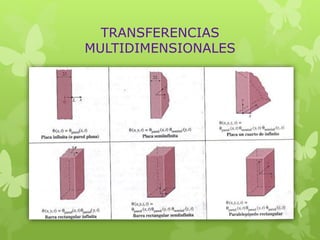
Este documento trata sobre la conducción de calor en régimen transitorio. Explica conceptos como el número de Biot y aplicaciones de sistemas concentrados. Presenta el análisis de un termopar esférico y discute modelos matemáticos de conducción unidimensional. También cubre temas como la conducción en sólidos semiinfinitos y el contacto entre sólidos, resolviendo ejercicios numéricos como ejemplos.