El documento analiza el impacto de la tecnología en la educación, resaltando la importancia de integrar herramientas digitales en el proceso de enseñanza. Se presentan estudios de caso que demuestran mejoras en el aprendizaje a través de plataformas interactivas. Además, se discuten desafíos y recomendaciones para su implementación eficaz.

1. TEMA 4 : PROPIEDADES MECANICAS DE LOS
METALES – ENSAYOS
DESTRUCTIVOS Y NO DESTRUCTIVOS –
TRABAJO PRACTICO Nº 4.-

2. Problema N°1
Una barra de acero templado de 2,5 m de longitud, de forma rectangular, de un
ancho de 4,0 cm y un espesor de 1,5 cm experimenta un alargamiento de 1,1
mm al aplicársele una carga de 6,5 ton.
Se pide determinar el módulo de elasticidad de dicho material.
2
6
0
0
0
0
/
10
462
,
2 cm
kgf
L
L
A
P
E
L
L
A
P
d
elasticida
de
Módulo
E
unitaria
n
Deformació
Tensión
E



















2,5 m
4 cm
1,5 cm

3. Problema N°2
Los datos que se indican en la tabla siguiente y en la figura adjunta
corresponden a un ensayo de tracción de una aleación no ferrosa. Sabiendo
que la probeta tenía una longitud calibrada original de 3 pulgadas, un diámetro
inicial de 1 pulgada y un diámetro final a la rotura de 0,5 pulgadas, se pide:
a) Determinar el límite convencional de fluencia 0,2 %.
b) Determinar el límite de proporcionalidad.
c) Determinar el módulo de elasticidad.
d) Determinar el límite de resistencia a la tracción.
e) Determinar la resistencia a la rotura.
f) Determinar el porcentaje de alargamiento a la rotura.
g) Determinar el porcentaje de reducción del área a la rotura.
P
ΔL
Carga (lbf) Deformación (pulg)
0,00 0,00
500 0,02
1000 0,04
1500 0,06
2000 0,08
2300 0,10
2450 0,12
2500 0,14
2460 0,16
2350 0,18
2200 0,20
2000 0,22
1700 0,24
1350 0,26

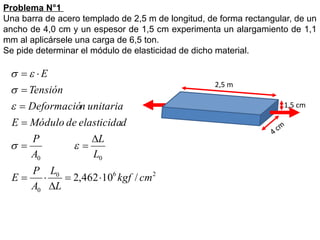
4. a) Determinar el límite convencional de fluencia 0,2 %.
Cuando el diagrama obtenido, no registre el fenómeno de fluencia, se define como
límite convencional de fluencia al que corresponde la carga capaz de producir un
alargamiento permanente del 0,2 % de la longitud inicial (Lo).
P[lbf]
ΔL[pulg]

5. 0,00
500,00
1000,00
1500,00
2000,00
2500,00
3000,00
0,00
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
0,22
0,24
0,26
Área inicial = π x R2
4
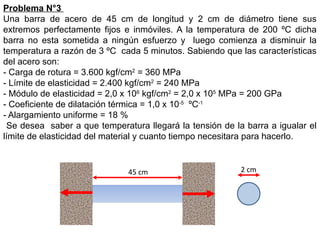
4) Límite convencional de fluencia= 2.941,18 lb/pulg2
1) 0,2% de L0 = 0,002 x 3 pulg = 0,006 pulg
Carga = 2.310 lbf
2) Tomando a partir del origen de coordenadas el 0,2 % de la longitud inicial
(0,006 pulg) se levanta una paralela al período proporcional hasta cortar la
curva de ensayo.
0
A
P


3)
0,006
P[lbf]
ΔL[pulg]

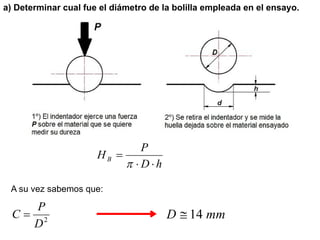
6. b) Determinar el límite de proporcionalidad.
Se observa en el diagrama que el comienzo está representado por una recta que pone
de manifiesto la proporcionalidad entre los alargamientos y las cargas que los
producen (ley de Hooke).
Límite de proporcionalidad: valor de la máxima tensión aplicable sin que se produzcan
deformaciones permanentes en el material.
0,00
500,00
1000,00
1500,00
2000,00
2500,00
3000,00
0,00
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
0,22
0,24
0,26
2
0
lbf/pulg
2.546,47


prop
prop
A
P


P[lbf]
ΔL[pulg]

7. c) Determinar el módulo de elasticidad.
2
4
0
0
0
0
lbf/pulg
10
9,549
1









E
l
l
A
P
A
P
E
A
P
E
prop
prop



0,00
500,00
1000,00
1500,00
2000,00
2500,00
3000,00
0,00
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
0,22
0,24
0,26
P[lbf]
ΔL[pulg]

8. d) Determinar el límite de resistencia a la tracción.
El límite de resistencia a la tracción es el valor de la máxima tensión, a partir de la cual
la deformación se localiza en una zona de la probeta, provocando un estrechamiento
de las secciones que llevan a la rotura (zona de estricción).
0,00
500,00
1000,00
1500,00
2000,00
2500,00
3000,00
0,00
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
0,22
0,24
0,26
2
max
0
max
max
lb/pulg
3.183,09




A
P
P[lbf]
ΔL[pulg]

9. e) Determinar la resistencia a la rotura.
2
0
lb/pulg
1.718,87


r
r
r
A
P


0,00
500,00
1000,00
1500,00
2000,00
2500,00
3000,00
0,00
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
0,22
0,24
0,26
P=1.350 lbf
P[lbf]
ΔL[pulg]

10. f) Determinar el porcentaje de alargamiento a la rotura:
δ =  L x 100 = 8,67 %
Lo
0,00
500,00
1000,00
1500,00
2000,00
2500,00
3000,00
0,00
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
0,22
0,24
0,26
P[lbf]
ΔL[pulg]

11. g) Determinar el porcentaje de reducción del área:
 (%) = (So – Sf) x 100 = 75,00 %
So

12. Problema N°3
Una barra de acero de 45 cm de longitud y 2 cm de diámetro tiene sus
extremos perfectamente fijos e inmóviles. A la temperatura de 200 ºC dicha
barra no esta sometida a ningún esfuerzo y luego comienza a disminuir la
temperatura a razón de 3 ºC cada 5 minutos. Sabiendo que las características
del acero son:
- Carga de rotura = 3.600 kgf/cm2
= 360 MPa
- Límite de elasticidad = 2.400 kgf/cm2
= 240 MPa
- Módulo de elasticidad = 2,0 x 106
kgf/cm2
= 2,0 x 105
MPa = 200 GPa
- Coeficiente de dilatación térmica = 1,0 x 10-5
ºC-1
- Alargamiento uniforme = 18 %
Se desea saber a que temperatura llegará la tensión de la barra a igualar el
límite de elasticidad del material y cuanto tiempo necesitara para hacerlo.
45 cm 2 cm

13. Dilatación lineal es la variación de la longitud de un cuerpo, como respuesta a
una variación en la temperatura.
Y se calcula con la siguiente fórmula:
T
l
l 



 
0








1
1
0
l
l
T
Se desea saber a que temperatura llegará la tensión de la barra a igualar el
límite de elasticidad del material y cuanto tiempo necesitara para hacerlo.
E
prop 
 

E
prop

 
    i
f
f
i
f T
T
T
porque
C
T
T
T
T 







 ,
0
200
  T
C
T
C
T
T f
f 








 200
200
min
200
min
5
3





x
T
C

14. Problema N°4
Al realizar un ensayo de dureza por el método Brinell de una plancha de
fundición se obtuvo un valor de dureza Brinell HB
= 148,55 kgf/mm2
. Sabiendo
que se obtuvo una impresión de flecha de 0,9 mm. Se pide:
a) Determinar cual fue el diámetro de la bolilla empleada en el ensayo.
b) Calcular el valor de la carga aplicada.
c) Calcular el diámetro de la impresión dejada por la bolilla en la plancha
de fundición.

15. h
D
P
HB




a) Determinar cual fue el diámetro de la bolilla empleada en el ensayo.
A su vez sabemos que:
2
D
P
C  mm
D 14


16. b) Calcular el valor de la carga aplicada.
2
D
C
P  kgf
P 5880

c) Calcular el diámetro de la impresión dejada por la bolilla en la plancha
de fundición.
2
2
2
d
D
D
h


 mm
d 863
,
6


17. Problema N°5
Suponga según la figura que se adjunta , que el material que se está
inspeccionando es una placa de cobre que tiene 1 pulgada de espesor, y que
en el punto “3” hay una discontinuidad que posee un espesor de ¼ de pulgada.
La discontinuidad contiene aire. Se pide estimar la relación entre las
intensidades (I/I0) de los rayos X en los puntos “1”, “2” y “3” de dicha figura.
Sabiendo que la placa de cobre está colocada sobre la película a una distancia
de 30 pulgadas de la fuente. La longitud de onda promedio de los rayos X es
de 0,098 Å .
DATOS:
Densidad del nitrógeno = 0,00116 G/CM3
Densidad del oxígeno = 0,00133 G/CM3
Densidad del cobre = 8,96 G/CM3
Coeficiente de absorción en masa del nitrógeno = 0,143 cm2
/g
Coeficiente de absorción en masa del oxígeno = 0,144 cm2
/g
Coeficiente de absorción en masa del cobre = 0,325 cm2
/g

18. 1 pulg
0,25 pulg
30 pulg
Intensidad del haz transmitido I:
)
exp(
0 x
I
I m 



 


19. Punto 1: Aire
Aire
79% N2
21% O2
x=30 pulg
)
(
exp
0
x
I
I
m 


 

aire = fO2
 O2
+ fN2
N2
𝜇𝑚
𝜇𝑚𝑁 2
𝜇𝑚𝑂2
𝜌𝑁 2
𝜌𝑂2
𝜌𝑎𝑖𝑟𝑒
maire = fO2
mO2
+ fN2
mN2
Película
impresionada por
Rayos X, color negro
989
,
0
0

I
I
30 pulg

20. Elemento Densidad
(g/cm3
)
m
(rayos X)  = 0,098 Å
(cm2
/g)
m
(neutrones)  = 1,08 Å
(cm2
/g)
Hidrógeno ------- 0,280 0,11
Berilio 1,85 0,131 0,0003
Carbono 2,2 0,142 0,00015
Nitrógeno 0,00116 0,143 0,048
Oxígeno 0,00133 0,144 0,00002
Magnesio 1,74 0,152 0,001
Aluminio 2,7 0,156 0,003
Silicio 2,33 0,159 0,001
Titanio 4,54 0,217 0,001
Hierro 7,87 0,265 0,015
Níquel 8,9 0,310 0,028
Cobre 8,96 0,325 0,021
Cinc 7,133 0,350 0,0055
Molibdeno 10,2 0,790 0,009
Estaño 7,3 1,170 0,002
Tungsteno 19,3 2,880 0,036
Plomo 11,34 3,500 0,0003

21. Punto 2: Placa de Cobre
El metal absorbe
casi todos los RX.
A la película no
llega casi nada de
RX, la que luego al
ser revelada tiene
una apariencia
transparente.
)
(
exp
0
x
I
I
m 


 

4
0
10
13
,
6
0006134
,
0 



I
I
lg
1 pu
Cu
Cu
m 

1 pulg

22. Punto 3: Placa de Cobre con la
discontinuidad
La cantidad de rayos X que llega
a la placa radiográfica es mayor
que en el caso anterior llegando
a impresionar parcialmente
dicha placa, la que luego al ser
revelada mostrará un color gris
más claro o más oscuro según
sea menor o mayor el espesor
de la falla o discontinuidad.
)
(
exp
0
x
I
I
m 


 

lg
25
,
0
lg
1
lg
1
pu
pu
x
pu
Cu
Cu
m




3
0
10
897
,
3
003897
,
0 



I
I
0,25 pulg

23. Problema N°6
Se tiene una plancha de níquel que tiene un espesor de 4 pulgadas y que se
sospecha que presenta una discontinuidad a una profundidad de 3 pulgadas.
Para verificar dicha sospecha se realizó un ensayo por ultrasonidos, utilizando
el método de pulso y eco. Se pide indicar el número de picos que mostró el
osciloscopio del instrumento y calcular los tiempos de aparición de cada uno
de ellos.
DATOS:
Velocidad de transmisión ultrasónica del níquel = 1,90 x 105
pulg/seg

24. Para el defecto:
Para el espesor:
t =3,1579 x 10-5
seg
t = 4,2105 x 10-5
seg
v
e
t
e
D
t
v
D






2
2
defecto
del
d
profundida
D 
 2
material
del
espesor
D 
 2
4 pulg
3 pulg

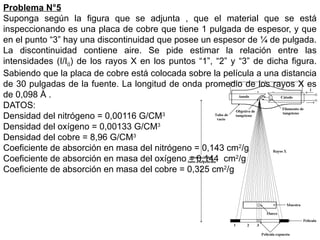
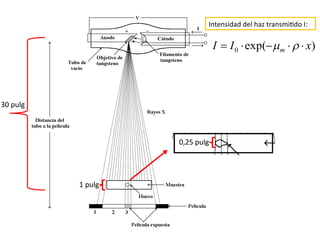
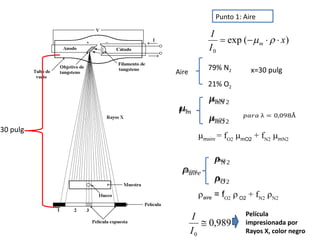
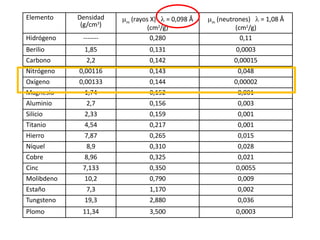
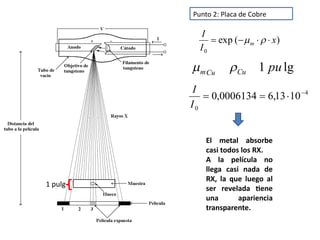
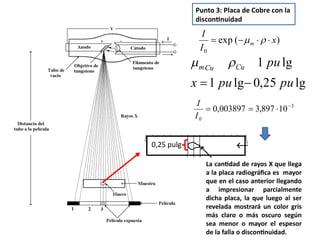
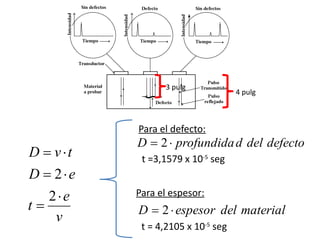
25. Problema N°7
Se tiene una pieza de magnesio que posee una velocidad de transmisión
ultrasónica de 2,013 x 105
pulgadas/segundo y una densidad de 1,74 g/cm3
. Se
pide determinar el valor del módulo de elasticidad expresado en psi.
DATOS:
Aceleración de la gravedad (g) = 386,09 pulg/seg2
Velocidad de propagación V[=] pulg/seg
E [=] psi [=] lb/pulg2
 [=] g/cm3
g [=] 386,09 pulg/seg2

g
E
v


 26
,
5
el valor 5,26 es un factor numérico de
conversión que incluye el coeficiente para la
conversión de unidades de g/cm3
a lb/pulg3
E = 6,600498 x 106
lb/pulg2
 6,60 x 106
psi