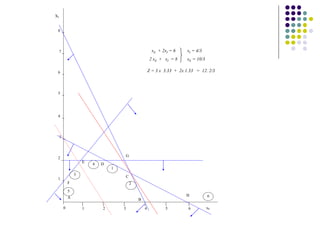
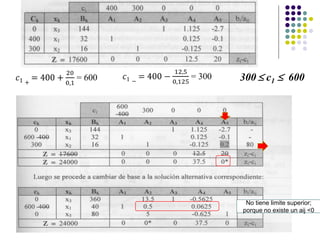
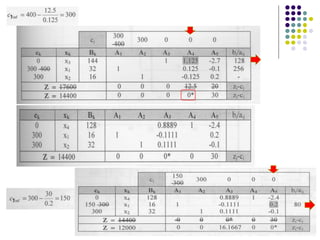
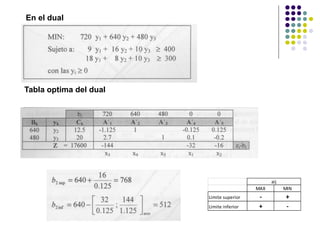
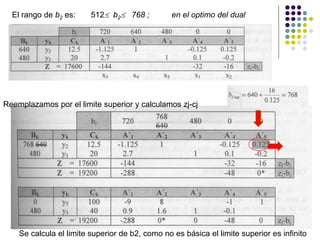
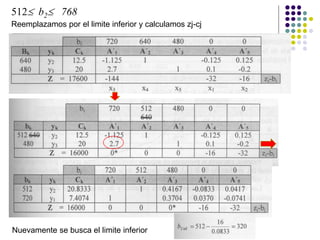
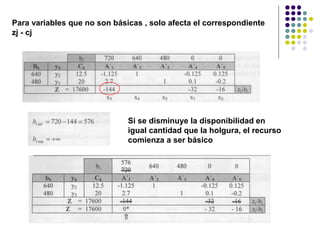
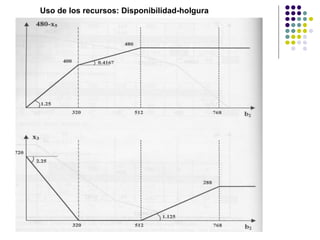
Este documento describe los diferentes tipos de análisis de sensibilidad que se pueden realizar en un problema de programación lineal. Explica que el análisis de sensibilidad estudia cómo cambios en el modelo original afectan la solución óptima. Estos cambios incluyen modificaciones en los coeficientes de la función objetivo, agregar nuevas actividades o restricciones, y cambios en los términos independientes de las restricciones. Además, provee ejemplos para ilustrar cómo se calculan los nuevos rangos de variación y lí

1. Análisis de
Sensibilidad

2. Análisis de Sensibilidad
Relación con el Problema Primal
El Análisis de Sensibilidad o Post óptimo estudia la sensibilidad de la solución
óptima cuando se realizan cambios en el modelo original:
1. En la función objetivo, c
2. Agregado de una nueva actividad (agregar una variable)
3. En los términos independientes, b
4. Agregado de una nueva restricción
Ejemplo de la primera clase:
Max z = 3xE + 2xI
sa. xE + 2xI  6
2xE + xI  8
- xE + xI  1
xI  2
xE , xI  0; xE : ton. Vendidas de pint. ext/día;
xI : ton. Vendidas de pint. int/día

3. |
1
|
2
|
3
|
4
|
5
|
6
1 _
2
3 _
4 _
5 _
6 _
7 _
8 _
XI
xE
0
A
B
C
D
E
F
G
H
1
4
2
5
3
6
xE + 2xI = 6
2 xE + xI = 8
xI = 4/3
xE = 10/3
Z = 3 x 3.33 + 2x 1.33 = 12. 2/3

4. -c 0 0
A I b
1ra. tabla
cBB-1A- c cBB-1
Z* = cBxB*=cBB-1 b
B-1A B-1 xB* = B-1 b
Tabla óptima
En forma tabular
y= cB B-1

5. Básica z xE xI s1 s2 s3 s4 Solución
z 1 -3 -2 0 0 0 0 0 Razón
s1 0 1 2 1 0 0 0 6 6
s2 0 (2) 1 0 1 0 0 8 4
s3 0 -1 1 0 0 1 0 1
s4 0 0 1 0 0 0 1 2
Básica z xE xI s1 s2 s3 s4 Solución
z 1 0 -1/2 0 3/2 0 0 12 Razón
s1 0 0 (3/2) 1 -1/2 0 0 2 4 / 3
xE 0 1 1/2 0 1/2 0 0 4 8
s3 0 0 3/2 0 1/2 1 0 5 10 / 3
s4 0 0 1 0 0 0 1 2 2
Básica z xE xI s1 s2 s3 s4 Solución
z 1 0 0 1/3 4/3 0 0 12 2/3
xI 0 0 1 2/3 -1/3 0 0 4 / 3
xE 0 1 0 -1/3 2/3 0 0 10 /3
s3 0 0 0 -1 1 1 0 3
s4 0 0 0 -2/3 1/3 0 1 2 / 3
















0
0
3
2
1
B
CB

6. 1.1 Cambio en los Coeficientes (Beneficios / Costos) de la función objetivo
(Actividades) - Cambios en la pendiente de z
-Supongamos que la Ganancia de xE ; cambia de 3 a 3 +1
- z = (3 +  1 ) xE + 2 xI
El cambio DÓNDE y QUÉ efectos producirá?
Rango de variación de ci: Determinemos el efecto que produce, utilizando el análisis
matricial:
(1) 1/3 - 1 /3  0 y 4/3 + 2/3 1  0 (2)
de (1)  1  1 y de (2 )  1  -2
-2   1  1 1  cE  4
xE xI s1 s2 s3 s4 Solución
z 0 0 1/3- 1/3 1 4/3 + 2/3 1 0 0 12 2/3 + 10 / 3 1
 





















1
0
3
/
1
3
/
2
0
1
1
1
0
0
3
/
2
3
/
1
0
0
3
/
1
3
/
2
0
,
0
,
3
,
2 1
1

B
CB

7. 1.2 Cambio en los Coeficientes (Beneficios / Costos) de la función objetivo
(Actividades)
Básica z xE xI s1 s2 s3 s4 Solución
z 1 0 0 1/3 4/3 0 0 12 2/3
xI 0 0 1 2/3 -1/3 0 0 4 / 3
xE 0 1 0 -1/3 2/3 0 0 10 /3
s3 0 0 0 -1 1 1 0 3
s4 0 0 0 -2/3 1/3 0 1 2 / 3
Rango de variación de CE:
(1) 1/3 - 1 /3  0 y (2) 4/3 + 2/3 1  0
de (1)  1  1 y de (2 )  1  -2
-2   1  1 ; 3-2  cE  1+3; 1  cE  4
Para un problema de maximización , zj- cj en el optimo es positivo, por lo que para
obtener un cero alternativo.
1. aij negativo, nos da el limite superior. Si no hay, no existe limite superior
2. aij positivo, nos da el limite inferior Si no hay, no existe limite inferior
En un caso de minimización es al revés
MAX MIN
Limite superior - +
Limite inferior + -
aij
En este rango se
mantiene constante la
estructura de la
solución optima
encontrada

8. Cambios que afectan la optimalidad
1- Cambios coeficientes de la función objetivo c+ c
Max z = ( c+ c ) x
z j - (c j +  cj ) = cBB-1 a j - (c j+  cj )
verificar z j - c j = 0 j B
z j - c j > 0 j B
Ej: Max z = 5x1 + 2x2 y modificamos c1 al limite Max de 4 ; z = 4x1+ 2 x2
Si C1=5, entones
z1 - c1 < 0 = -1
Se debe iterar de nuevo,
No es optima
y
zj
Básica z X1 X2 s1 s2 s3 s4 Solución
z 1 0 0.5 0 2.5 .0 0 20
s1 0 0 1.5 1 -0.5 0 0 2
X1 0 1 0.5 0 0.5 0 0 4
s3 0 0 1.5 0 0.5 1 0 5
s4 0 0 1 0 0 0 1 2
cBB-1A- c
zj= cBB-1A
Se recalcula el z j - c j de x1, en caso que sea negativo, debe buscarse el optimo
Para una variable no básica, un cambio en el coeficiente de la función objetivo de una
variable no básica afectará en , de la tabla optima, por el cambio en c (NB)

9. Curvas de oferta
 Gráfico C en f(X): en la tabla óptima se calcula el rango de C
de una actividad. Se grafica C en f(X).
 Para el límite superior de C se realiza una nueva iteración del MS, sobre
el cual se vuelve a calcular el limite superior de C. Se grafica C en f(X).
Se repite el procedimiento hasta que para cualquier aumento de C, X se
mantiene constante.
 El mismo procedimiento para el límite inferior de la Tabla Optima. Se
grafica C en f(X). Se repite el procedimiento hasta que X=0.
 Referencias:
La Programación Lineal en el proceso de decisión- Marín Palma Lara- ed. Macchi
Programación Lineal y su entorno- Miguel Miranda Ed Educa.

10. Ejemplo
Se busca el rango de variación de c1

11. 300  c1  600
No tiene limite superior;
porque no existe un aij <0

12. 1
1

13. X1 se va de la base
Curvas de oferta
Gráfico C en f(X): en la tabla
óptima se calcula el rango de C
de una actividad.
Se grafica C en Función de X1.

14. 2- Adición de una nueva actividad
Ejemplo: Fabricación y venta de una nueva pintura (NP), cuya utilidad en
miles de unidades monetarias por tonelada es: 4 y cuyos datos de producción
son: 2 ton de MPA/ton NP y 1 Ton MPB/ton NP.
Calcular los nuevos : z j - c j = cBB-1 aj - c j
y los nuevos : a’j= B-1 a j
Verificar que z j - cj sea:
 z j - cj > 0
 z j - cj = 0
 z j - cj < 0 , se verifica con las variables del dual
En caso que el z j - cj sea negativo, hay que volver a la tabla optima, es decir
iterar nuevamente, ya que se incrementara Z con la producción de esta
pintura. Se comienza a producir este nuevo producto
  2
4
0
0
1
2
0
,
0
,
3
/
4
,
3
/
1
*
1
























cj
aj
y
cj
zj
cj
a
B
C j
B

15. 3- Cambios en el segundo miembro de las restricciones
(términos independientes).
b b +  b  x^ B = B-1 (b +  b)
si x^ B  0
si x^ B < 0
Ej: 8 a 7 ( disponibilidad de materia prima B )
4- Agregado de una nueva restricción
 ai j xj  bi
Se verifica la factibilidad en el optimo del primal, se satisface o no la solución actual.
En caso de que se cumpla , no altera el optimo
Se no cumple, se debe utilizar el dual simple para volver a la factibilidad
Ej: x1  4 o x1 3
Cambios que afectan la factibilidad
j=1 a
n

16. Cambio máximo en la disponibilidad de recursos
- Materia Prima A de 6 a 6+  1
* El cambio solo afectará el segundo miembro de cada iteración.
* Cambios en la tabla óptima
B-1 ( b + b ) : 12,66 + 1/3  1
4/3 + 2/3  1 (1)  0
10/3 - 1/3  1 (2)  0
3 - 1 1 (3)  0
2/3 - 2/3  1 (4)  0
Un cambio de este tipo afecta la factibilidad
Para determinar el intervalo admisible de  1
* si  1 >0: (1) se cumple siempre
de (2)   1  5
de (3)   1  3   1  1, (se elige el menor rango de variación)
de (4 )  1 1
* si  1 <0 : (2), (3) y (4) se satisfacen siempre.
(1)   1  -2
 -2  1  1 ; 6-2 b1  6+1  4 b1 7
Básica z xE xI s1 s2 s3 s4 Solución
z 1 0 0 1/3 4/3 0 0 12,66
xI 0 0 1 2/3 -1/3 0 0 4 / 3
xE 0 1 0 -1/3 2/3 0 0 10 /3
s3 0 0 0 -1 1 1 0 3
s4 0 0 0 -2/3 1/3 0 1 2 / 3

17. Curvas y en f(b), Z en f(b), Uso de recursos en f(b)
 En la tabla óptima se calcula el rango de b de una disponibilidad
(de un recurso). Se grafican las coordenadas correspondientes de los tres
gráficos en f(b).
 Para el límite superior de b se realiza una nueva iteración del MS, sobre el
cual se vuelve a calcular el limite superior de b. Se continúa el gráfico de las
tres curvas f(b). Se repite el procedimiento hasta que para cualquier
aumento de b no se modifican las curvas.
 El mismo procedimiento para el límite inferior de la TO. Se grafican las
curvas. Se repite el procedimiento hasta que b=0.
 Se trabaja en las tablas optimas del dual
 Referencias:
La Programación Lineal en el proceso de decisión- Marín Palma Lara- ed. Macchi
Programación Lineal y su entorno- Miguel Miranda Ed Educa.

18. En el dual
Tabla optima del dual
MAX MIN
Limite superior - +
Limite inferior + -
aij

19. El rango de b2 es: 512 b2 768 ; en el optimo del dual
Reemplazamos por el limite superior y calculamos zj-cj
Se calcula el limite superior de b2, como no es básica el limite superior es infinito

20. Reemplazamos por el limite inferior y calculamos zj-cj
Nuevamente se busca el limite inferior
512 b2 768

21. Reemplazamos por el limite inferior y calculamos zj-cj
Ya no se puede seguir iterando , porque al pretender ingresar y2, no puede salir ninguna

22. Curvas y en f(b), Z en f(b), Uso de recursos en f(b)
 En la tabla óptima se calcula el rango de b de una disponibilidad
(de un recurso).
En el rango de variación de b se mantiene constante el valor marginal del
recurso

23. Para variables que no son básicas , solo afecta el correspondiente
zj - cj
Si se disminuye la disponibilidad en
igual cantidad que la holgura, el recurso
comienza a ser básico

24. Producción de x2 y valor marginal de b3
x1

25. Uso de los recursos: Disponibilidad-holgura