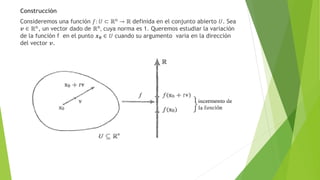
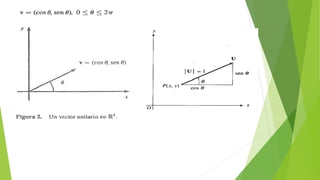
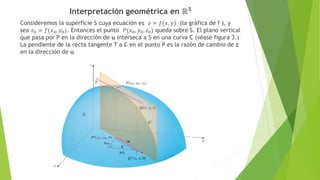
1) El documento introduce el concepto de derivada direccional, que representa la variación de una función cuando su argumento varía en una dirección dada. 2) Se define formalmente la derivada direccional como el límite de la variación de la función entre dos puntos dividido por la distancia entre esos puntos a medida que la distancia tiende a cero. 3) Se muestran ejemplos del cálculo de derivadas direccionales en R2 y R3 y su relación con las derivadas parciales.

1. Unidad 3 parte 3
continuación

2. Derivadas direccionales
Introducción

3. Construcción
Consideremos una función 𝑓: 𝑈 ⊂ ℝn → ℝ definida en el conjunto abierto 𝑈. Sea
𝒗 ∈ ℝn
, un vector dado de ℝn
, cuya norma es 1. Queremos estudiar la variación
de la función f en el punto 𝒙𝟎 ∈ 𝑈 cuando su argumento varia en la dirección
del vector 𝒗.

4. Note que la variable vectorial 𝒙 ∈ 𝑈 se mueve t unidades en la dirección del vector 𝒗
pasando del punto 𝒙𝟎 ∈ 𝑈 al punto 𝑥0 + 𝑡𝒗. La magnitud de esta variación es
𝑡𝒗 = 𝑡 𝒗 = 𝑡 1 = 𝑡 = |𝑡|
Así, tomando el cociente del incremento de la función 𝑓 𝒙𝟎 + 𝑡𝒗 − 𝑓 𝒙𝟎 , dividiendo
entre t y tomando el límite cuando t tiende a cero, obtenemos la manera de variar de
f en 𝒙𝟎 en la dirección de v. A esto lo llamamos derivada direccional de f en 𝒙𝟎 en la
dirección de v.
Definición (derivada direccional)
Sea 𝑓: 𝑈 ⊂ ℝn
→ ℝ una función definida en el conjunto abierto 𝑈 de ℝn
y sea 𝒙𝟎 ∈
𝑈 un punto dado de 𝑈. Sea 𝒗 ∈ ℝn
un vector unitario dado. Se define la derivada de
la función f en 𝒙𝟎, en la dirección del vector 𝒗, denotada por
𝜕𝑓
𝜕𝑣
(𝒙𝟎) o 𝐷𝑣𝑓(𝒙𝟎),
como el límite
𝜕𝑓
𝜕𝒗
𝒙𝟎 = 𝐷𝒗𝑓 𝒙𝟎 = 𝑓′ 𝒙𝟎; 𝑣 = lim
𝑡→0
𝑓 𝒙𝒐+𝑡𝑣 −𝑓(𝒙𝟎)
𝑡
= lim
ℎ→0
𝑓 𝒙𝒐+ℎ𝒗 −𝑓(𝒙𝟎)
ℎ
ℎ = 𝑡

7. Sea 𝑈 ⊂ ℝ2
, 𝐱𝟎 = 𝑥0, 𝑦0 , 𝑣 = 𝑎, 𝑏 = (cos 𝜃, 𝑠𝑒𝑛 𝜃)
𝑣 = 𝑎2 + 𝑏2 = 1
𝑓′ 𝒙𝟎; 𝒗 = lim
ℎ→0
𝑓 𝒙𝒐 + ℎ𝒗 − 𝑓(𝒙𝟎)
ℎ
𝑓′
𝑥0, 𝑦0 ; (𝑎, 𝑏) = lim
ℎ→0
𝑓 (𝑥0, 𝑦0) + ℎ(𝑎, 𝑏) − 𝑓(𝑥0, 𝑦0)
ℎ
𝑓′ 𝑥0, 𝑦0 ; (𝑎, 𝑏) = lim
ℎ→0
𝑓 (𝑥0, 𝑦0) + (ℎ𝑎, ℎ𝑏) − 𝑓(𝑥0, 𝑦0)
ℎ
𝑓′
𝑥0, 𝑦0 ; (𝑎, 𝑏) = lim
ℎ→0
𝑓 (𝑥0 + ℎ𝑎, 𝑦0 + ℎ𝑏) − 𝑓(𝑥0, 𝑦0)
ℎ
James Stewart

8. Leithold-Cálculo trascendentes tempranas y Larson
𝐷𝒗𝑓 𝒙𝟎 = lim
ℎ→0
𝑓 𝒙𝒐 + ℎ𝒗 − 𝑓(𝒙𝟎)
ℎ
𝐷𝒗𝑓 𝑥0, 𝑦0 = lim
ℎ→0
𝑓 (𝑥0, 𝑦0) + ℎ(cos 𝜃 , 𝑠𝑒𝑛 𝜃) − 𝑓(𝑥0, 𝑦0)
ℎ
𝐷𝒗𝑓 𝑥0, 𝑦0 = lim
ℎ→0
𝑓 (𝑥0, 𝑦0) + (ℎ𝑐𝑜𝑠 𝜃, ℎ𝑠𝑒𝑛 𝜃) − 𝑓(𝑥0, 𝑦0)
ℎ
𝐷𝒗𝑓 𝑥0, 𝑦0 = lim
ℎ→0
𝑓 (𝑥0+ℎ𝑐𝑜𝑠 𝜃,𝑦0+ℎ𝑠𝑒𝑛 𝜃) −𝑓(𝑥0,𝑦0)
ℎ
Equivalencia con el Apostol
𝜕𝑓
𝜕𝒗
𝒙 = lim
ℎ→0
𝑓 𝒙 + ℎ𝒗 − 𝑓(𝒙)
ℎ
Si hacemos 𝒗 = 𝒚 y 𝒙 = 𝒂
Obtenemos que
𝜕𝑓
𝜕𝒗
𝒙 = 𝑓′(𝒂; 𝒚)

9. Recordatorio derivada parcial
Apostol
𝐷𝑘𝑓 𝒂 = 𝑓′ 𝒂; 𝒆𝒌 = lim
ℎ→0
𝑓 𝒂 + ℎ𝒆𝒌 − 𝑓(𝒂)
ℎ
𝒆𝒌: k-ésimo vector coordenado unitario.
Nota: 𝒂 ∈ ℝ𝑛
Si 𝑘 = 1,entonces 𝐷1𝑓 𝒂 ( derivada parcial con respecto a 𝑥, es decir, en la dirección
del eje 𝑥
𝐷1𝑓 𝒂 = 𝑓′
𝒂; 𝒆𝟏 = lim
ℎ→0
𝑓 𝒂 + ℎ𝒆𝟏 − 𝑓(𝒂)
ℎ
Si hacemos 𝒂 = (𝑎, 𝑏), encontramos que
𝐷1𝑓 (𝑎, 𝑏) = 𝑓′
(𝑎, 𝑏); 𝒆𝟏 = lim
ℎ→0
𝑓 (𝑎, 𝑏) + ℎ𝒆𝟏 − 𝑓(𝑎, 𝑏)
ℎ
𝐷1𝑓 (𝑎, 𝑏) = 𝑓′ (𝑎, 𝑏); (1,0) = lim
ℎ→0
𝑓 (𝑎, 𝑏) + ℎ(1,0) − 𝑓(𝑎, 𝑏)
ℎ
= lim
ℎ→0
𝑓 (𝑎, 𝑏) + (ℎ, 0) − 𝑓((𝑎, 𝑏))
ℎ
= lim
ℎ→0
𝑓 𝑎 + ℎ, 𝑏 − 𝑓(𝑎, 𝑏)
ℎ
Si ℎ = ∆𝑥, entonces generalizamos, ya no es en (𝑎, 𝑏) sino en 𝑥, 𝑦 .
𝐷1𝑓 (𝑥, 𝑦) = lim
∆𝑥→0
𝑓 𝑥 + ∆𝑥, 𝑦 − 𝑓(𝑥, 𝑦)
∆𝑥

10. Si 𝑘 = 2,entonces 𝐷2𝑓 𝒂 ( derivada parcial con respecto a 𝑦, es decir, en la
dirección del eje 𝑦)
𝐷2𝑓 𝒂 = 𝑓′
𝑎; 𝒆𝟐 = lim
ℎ→0
𝑓 𝒂 + ℎ𝒆𝟐 − 𝑓(𝒂)
ℎ
Si hacemos 𝒂 = (𝑎, 𝑏), encontramos que
𝐷2𝑓 (𝑎, 𝑏) = 𝑓′
(𝑎, 𝑏); 𝒆𝟐 = lim
ℎ→0
𝑓 (𝑎, 𝑏) + ℎ𝒆𝟐 − 𝑓(𝑎, 𝑏)
ℎ
𝐷2𝑓 (𝑎, 𝑏) = 𝑓′
(𝑎, 𝑏); (0,1) = lim
ℎ→0
𝑓 (𝑎, 𝑏) + ℎ(0,1) − 𝑓(𝑎, 𝑏)
ℎ
= lim
ℎ→0
𝑓 (𝑎, 𝑏) + (0, ℎ) − 𝑓((𝑎, 𝑏))
ℎ
= lim
ℎ→0
𝑓 𝑎, 𝑏 + ℎ − 𝑓(𝑎, 𝑏)
ℎ
Si ℎ = ∆𝑦, entonces generalizamos, ya no es en (𝑎, 𝑏) sino en 𝑥, 𝑦 .
𝐷2𝑓 (𝑥, 𝑦) = lim
∆𝑦→0
𝑓 𝑥, 𝑦 + ∆𝑦 − 𝑓(𝑥, 𝑦)
∆𝑦

12. Interpretación geométrica en ℝ𝟑
Consideremos la superficie S cuya ecuación es 𝑧 = 𝑓 𝑥, 𝑦 (la gráfica de f ), y
sea 𝑧0 = 𝑓(𝑥0, 𝑦0). Entonces el punto 𝑃(𝑥0, 𝑦0, 𝑧0) queda sobre S. El plano vertical
que pasa por P en la dirección de u interseca a S en una curva C (véase figura 3.)
La pendiente de la recta tangente T a C en el punto P es la razón de cambio de z
en la dirección de u

14. Ejemplo: Aplique la definición para calcular 𝑓′(𝒂; 𝒚) si 𝑓 𝑥, 𝑦 = 12 − 𝑥2 − 4𝑦2 y 𝒚
es el vector unitario en la dirección en la dirección
1
6
𝜋.
Solución
𝒚 = 𝑐𝑜𝑠 𝜃 𝒊 + 𝑠𝑒𝑛 𝜃 𝒋 = 𝑐𝑜𝑠
1
6
𝜋 𝒋 + 𝑠𝑒𝑛
1
6
𝜋 𝒋 =
3
2
𝒊 +
1
2
𝒋
𝒚 =
3
2
2
+
1
2
2
=
3
4
+
1
4
= 1 = 1
𝒚 =
3
2
,
1
2
𝑓′
𝒂; 𝒚 = 𝑓′
𝑥, 𝑦 ;
3
2
,
1
2
= lim
ℎ→0
𝑓 𝑥, 𝑦 + ℎ
3
2 ,
1
2 − 𝑓(𝑥, 𝑦)
ℎ
= lim
ℎ→0
𝑓 𝑥, 𝑦 +
3
2
ℎ,
1
2
ℎ − 𝑓(𝑥, 𝑦)
ℎ
= lim
ℎ→0
𝑓 𝑥 +
3
2 ℎ, 𝑦 +
1
2 ℎ − 𝑓(𝑥, 𝑦)
ℎ

15. = lim
ℎ→0
12 − 𝑥 +
3
2
ℎ
2
− 4 𝑦 +
1
2
ℎ
2
− 12 − 𝑥2 − 4𝑦2
ℎ
= lim
ℎ→0
12 − 𝑥2
+ 3ℎ𝑥 +
3
4 ℎ2
− 4 𝑦2
+ ℎ𝑦 +
1
4 ℎ2
− 12 − 𝑥2
− 4𝑦2
ℎ
= lim
ℎ→0
12 − 𝑥2 − 3ℎ𝑥 −
3
4
ℎ2 − 4𝑦2 − 4ℎ𝑦 − ℎ2 − 12 − 𝑥2 − 4𝑦2
ℎ
= lim
ℎ→0
12 − 𝑥2
− 3ℎ𝑥 −
3
4
ℎ2
− 4𝑦2
− 4ℎ𝑦 − ℎ2
− 12 + 𝑥2
+ 4𝑦2
ℎ
= lim
ℎ→0
− 3ℎ𝑥 −
7
4
ℎ2 − 4ℎ𝑦
ℎ
= lim
ℎ→0
ℎ − 3𝑥 −
7
4
ℎ − 4𝑦
ℎ
= lim
ℎ→0
− 3𝑥 −
7
4
ℎ − 4𝑦 = − 3𝑥 − 4𝑦

16. Otra forma
D𝐮f x, y = lim
ℎ→0
𝑓 (𝑥 + ℎ𝑎, 𝑦0 + ℎ𝑏) − 𝑓(𝑥, 𝑦)
ℎ
= lim
ℎ→0
𝑓 (𝑥 + ℎ
3
2 , 𝑦0 + ℎ
1
2) − 𝑓(𝑥, 𝑦)
ℎ
= lim
ℎ→0
12 − 𝑥 +
3
2 ℎ
2
− 4 𝑦 +
1
2 ℎ
2
− 12 − 𝑥2
− 4𝑦2
ℎ
Demostración: forma 1

18. Sean 𝑥, 𝑦, 𝑎 y 𝑏 fijas de manera que 𝑔 𝑡 = 𝑓(𝑥 + 𝑡𝑎, 𝑦 + 𝑡𝑏) es una función de
una variable t.
𝑔′ 𝑡 = lim
ℎ→0
𝑔 𝑡+ℎ −𝑔(𝑡)
ℎ
𝑔′
0 = lim
ℎ→0
𝑔 0 + ℎ − 𝑔(0)
ℎ
𝑔′ 0 = lim
ℎ→0
𝑔 ℎ − 𝑔(0)
ℎ
𝑔′
0 = lim
ℎ→0
𝑓 𝑥 + ℎ𝑎, 𝑦 + ℎ𝑏 − 𝑓(𝑥, 𝑦)
ℎ
= 𝐷𝒖𝑓(𝑥, 𝑦)
Por la regla de la cadena
𝑔′
𝑡 = 𝑓𝑥+𝑡𝑎 𝑥 + 𝑡𝑎, 𝑦 + 𝑡𝑏 .
𝑑 𝑥 + 𝑡𝑎
𝑑𝑡
+ 𝑓𝑦+𝑡𝑏 𝑥 + 𝑡𝑎, 𝑦 + 𝑡𝑏 .
𝑑 𝑦 + 𝑡𝑏
𝑑𝑡
𝑔′ 𝑡 = 𝑓𝑥+𝑡𝑎 𝑥 + 𝑡𝑎, 𝑦 + 𝑡𝑏 .
𝑑 𝑥 + 𝑡𝑎
𝑑𝑡
+ 𝑓𝑦+𝑡𝑏 𝑥 + 𝑡𝑎, 𝑦 + 𝑡𝑏 .
𝑑 𝑦 + 𝑡𝑏
𝑑𝑡
𝑔′ 𝑡 = 𝑓𝑥+𝑡𝑎 𝑥 + 𝑡𝑎, 𝑦 + 𝑡𝑏 . 𝑎 + 𝑓𝑦+𝑡𝑏 𝑥 + 𝑡𝑎, 𝑦 + 𝑡𝑏 . 𝑏
𝑔′
0 = 𝑓𝑥+(0)𝑎 𝑥 + (0)𝑎, 𝑦 + (0)𝑏 . 𝑎 + 𝑓𝑦+(0)𝑏 𝑥 + (0)𝑎, 𝑦 + (0)𝑏 . 𝑏
𝑔′
0 = 𝑓𝑥 𝑥, 𝑦 . 𝑎 + 𝑓𝑦(𝑥, 𝑦). 𝑏

19. Así tenemos que
𝑔′ 0 = 𝐷𝑢𝑓(𝑥, 𝑦)
𝑔′
0 = 𝑓𝑥 𝑥, 𝑦 . 𝑎 + 𝑓𝑦(𝑥, 𝑦). 𝑏
Concluimos que
𝐷𝒖𝑓 𝑥, 𝑦 = 𝑓𝑥 𝑥, 𝑦 . 𝑎 + 𝑓𝑦(𝑥, 𝑦). 𝑏
O también
𝐷𝒖𝑓 𝑥, 𝑦 = 𝑓𝑥 𝑥, 𝑦 . cos 𝜃 + 𝑓𝑦 𝑥, 𝑦 . 𝑠𝑒𝑛𝜃
Ejemplo: Calcule 𝐷𝒖𝑓 𝑥, 𝑦 si 𝑓 𝑥, 𝑦 = 12 − 𝑥2
− 4𝑦2
y es el vector unitario en
la dirección de
𝜋
6
.
𝜃 =
𝜋
6
𝒖 = cos 𝜃 𝒊 + 𝑠𝑒𝑛 𝜃 𝒋 = 𝒄𝒐𝒔
𝜋
6
𝒊 + 𝑠𝑒𝑛
𝜋
6
𝒋 =
3
2
𝒊 +
1
2
𝒋
𝑎 =
3
2
𝑏 =
1
2
𝐷𝒖𝑓 𝑥, 𝑦 = 𝑓𝑥 𝑥, 𝑦 . 𝑎 + 𝑓𝑦 𝑥, 𝑦 . 𝑏 = −2𝑥
3
2
+ −8𝑦
1
2
= − 3𝑥 − 4𝑦

20. Nota: Si 𝒖 = 𝑎, 𝑏 = 1,0 entonces
𝐷𝒖𝑓 𝑥, 𝑦 = 𝑓𝑥 𝑥, 𝑦 . 1 + 𝑓𝑦 𝑥, 𝑦 . 0 = 𝑓𝑥 𝑥, 𝑦
Si 𝑢 = 𝑎, 𝑏 = 0,1 entonces
𝐷𝒖𝑓 𝑥, 𝑦 = 𝑓𝑥 𝑥, 𝑦 . 0 + 𝑓𝑦 𝑥, 𝑦 . 1 = 𝑓𝑦 𝑥, 𝑦
Ejemplo: calcular la derivada direccional de 𝑓 𝑥, 𝑦 = 𝑥2𝑠𝑒𝑛 2𝑦 enen 1,
𝜋
2
en
la dirección de 𝒗 = 3𝒊 − 4𝒋
𝒖 =
𝒗
𝒗
=
(3,−4)
3 2+ −4 2
=
(3,−4)
25
=
3
25
, −
4
25
=
3
5
, −
4
5
𝑎 =
3
5
, 𝑏 = −
4
5
𝐷𝒖𝑓 𝑥, 𝑦 = 𝑓𝑥 𝑥, 𝑦 . 𝑎 + 𝑓𝑦(𝑥, 𝑦). 𝑏
𝐷𝒖𝑓 𝑥, 𝑦 = 2𝑥𝑠𝑒𝑛 2𝑦.
3
5
+ 2𝑥2
cos 2𝑦 . −
4
5
𝐷𝒖𝑓 𝑥, 𝑦 =
6
5
𝑥 𝑠𝑒𝑛 2𝑦 −
8
5
𝑥2 cos 2𝑦
𝐷𝒖𝑓 1,
𝜋
2
=
6
5
(1) 𝑠𝑒𝑛 2
𝜋
2
−
8
5
(1)2
cos 2
𝜋
2
=
6
5
𝑠𝑒𝑛 𝜋 −
8
5
(1)2
cos 𝜋 =
6
5
0 −
8
5
−1 =
8
5

21. Vector gradiente
Vector gradiente
La derivada direccional puede expresarse como el producto de dos vectores
𝐷𝒖𝑓 𝑥, 𝑦 = 𝑓𝑥 𝑥, 𝑦 . 𝑎 + 𝑓𝑦 𝑥, 𝑦 . 𝑏 = 𝑎, 𝑏 ∙ 𝑓𝑥 𝑥, 𝑦 , 𝑓𝑦 𝑥, 𝑦
= (𝑎 𝒊 + 𝑏 𝒋) ∙ 𝑓𝑥 𝑥, 𝑦 𝒊 + 𝑓𝑦 𝑥, 𝑦 𝒋
𝛻𝑓 𝑥, 𝑦 = 𝑓𝑥 𝑥, 𝑦 , 𝑓𝑦 𝑥, 𝑦 =
𝜕𝑓
𝜕𝑥
,
𝜕𝑓
𝜕𝑦
=
𝜕𝑧
𝜕𝑥
,
𝜕𝑧
𝜕𝑦
= 𝑓𝑥 𝑥, 𝑦 𝒊 + 𝑓𝑦 𝑥, 𝑦 𝒋 =
𝜕𝑓
𝜕𝑥
𝒊 +
𝜕𝑓
𝜕𝑦
𝒋

22. Definición (gradiente de una función de dos variables)
Si f es una función de las dos variables 𝑥 y 𝑦, 𝑓𝑥, 𝑓𝑦 existen, entonces el
gradiente de f denotado por 𝛻𝑓( lease “del f”), esta definido por
𝛁𝒇 𝑥, 𝑦 = 𝑓𝑥 𝑥, 𝑦 𝒊 + 𝑓𝑦 𝑥, 𝑦 𝒋 =
𝜕𝑓
𝜕𝑥
𝒊 +
𝜕𝑓
𝜕𝑦
𝒋
Nota: Otra notación usual para el gradiente de f es 𝑔𝑟𝑎𝑑 𝑓 𝑥, 𝑦 . El gradiente de
f es un vector en el plano.
Ejemplo: Calcule el gradiente de 𝑓(𝑥, 𝑦 = 𝑦 𝑙𝑛 𝑥 + 𝑥𝑦2
en el punto (1,2)
𝛁𝒇 𝑥, 𝑦 =
𝜕𝑓
𝜕𝑥
𝒊 +
𝜕𝑓
𝜕𝑦
𝒋 =
1
𝑥
𝑦 + 𝑦2 𝒊 + 𝑙𝑛 𝑥 + 2𝑥𝑦 𝒋
𝛁𝒇 1,1 =
1
1
1 + 12 𝒊 + 𝑙𝑛 1 + 2(1)(1) 𝒋 = 2 + 4 𝒊 + 0 + 4 𝒋 = 6 𝒊 + 4𝒋
𝐷𝒖𝑓 𝑥, 𝑦 = 𝑓𝑥 𝑥, 𝑦 . 𝑎 + 𝑓𝑦 𝑥, 𝑦 . 𝑏 = 𝑎, 𝑏 ∙ 𝑓𝑥 𝑥, 𝑦 , 𝑓𝑦 𝑥, 𝑦 = 𝒖 ∙ 𝛁𝒇 𝑥, 𝑦
= 𝛁𝒇 𝑥, 𝑦 ∙ 𝒖

23. Ejemplo: determine la derivada direccional de la función 𝑓 𝑥, 𝑦 = 𝑥2
𝑦3
− 4𝑦 en
el punto (2, −1) en la dirección del vector 𝑣 = 2 𝒊 + 5 𝒋
Solución
𝛁𝒇 𝑥, 𝑦 = 2𝑥𝑦3
, 3𝑥2
𝑦2
− 4
𝛁𝒇 2, −1 = 2 2 −1 3
, 3 2 2
−1 2
− 4 = (−4,8)
𝒖 =
𝒗
𝒗
=
(2,5)
2 2 + 5 2
=
(2,5)
29
=
2
29
,
5
29
𝑎 =
2
29
, 𝑏 =
5
29
𝐷𝒖𝑓 2, −1 = 𝛁𝒇 2, −1 ∙ 𝒖 = −4,8 ∙
2
29
,
5
29
= −
8
29
+
40
29
=
32
29
Ejercicio: Hallar la derivada direccional de 𝑓 𝑥, 𝑦 = 3𝑥2 − 2𝑦2 en −
3
4
, 0 en
la dirección del segmento de recta que va 𝑃 −
3
4
, 0 a 𝑄(0,1).
Nota: 𝒖 = 𝑷𝑸 = 0 − −
3
4
, 1 − 0 =
3
4
, 1

26. Nota:
Si 𝛁𝒇 𝑥, 𝑦 = 0 entonces 𝐷𝒖𝑓 𝑥, 𝑦 = 0 para cualquier 𝒖.
Ahora, si 𝛁𝒇 𝑥, 𝑦 ≠ 0 y si 𝜃 es la medida del ángulo en radianes entre los dos
vectores 𝒖 y 𝛁𝒇 𝑥, 𝑦 entonces
𝐷𝒖𝑓 𝑥, 𝑦 = 𝛁𝒇 𝑥, 𝑦 ∙ 𝒖 = 𝒖 𝛁𝒇 𝑥, 𝑦 cos 𝜃 = 1 𝛁𝒇 𝑥, 𝑦 cos 𝜃
= 𝛁𝒇 𝑥, 𝑦 cos 𝜃
¿Qué nos dice este resultado?
El valor máximo de 𝐷𝒖𝑓 𝑥, 𝑦 ocurre cuando cos 𝜃 = 1, es decir, 𝜃 = 0. Por tanto,
𝐷𝒖𝑓 𝑥, 𝑦 y 𝑢 están en la misma dirección.
El valor máximo de 𝐷𝒖𝑓 𝑥, 𝑦 es 𝛁𝒇 𝑥, 𝑦 .
De manera similar, el valor mínimo de 𝐷𝒖𝑓 𝑥, 𝑦 se presenta cuando cos 𝜃 = −1, es
decir, 𝜃 = 𝜋. Por tanto, 𝐷𝒖𝑓 𝑥, 𝑦 y 𝑢 tienen dirección opuesta. El valor mínimo de
𝐷𝒖𝑓 𝑥, 𝑦 es − 𝛁𝒇 𝑥, 𝑦
Nota: 𝐷𝒖𝑓 𝑥, 𝑦 = 𝛁𝒇 𝑥, 𝑦 cos 𝜃
−1 ≤ 𝑐𝑜𝑠 𝜃 ≤ 1
−1 ≤
𝐷𝒖𝑓 𝑥, 𝑦
𝛁𝒇 𝑥, 𝑦
≤ 1
− 𝛁𝒇 𝑥, 𝑦 ≤ 𝐷𝒖𝑓 𝑥, 𝑦 ≤ 𝛁𝒇 𝑥, 𝑦

35. Funciones de tres variables