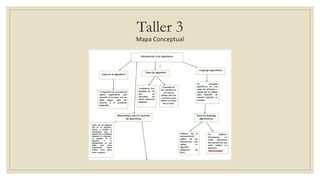
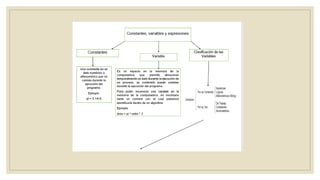
Este documento presenta la temática de un curso de Lógica y Algoritmos. Incluye temas como lógica proposicional, lógica de predicados, conjuntos, operaciones básicas sobre conjuntos, relaciones, funciones, inducción finita y más. El documento proporciona una lista detallada de los subtemas que se cubrirán en el curso.

1. UAM
UNIVERSIDAD
AMERICANA
Lic. En informática con Énfasis en Computo Gerencial
Nombre
Jostin Barba
Materia
Lógica y algoritmo
Profesora
Carmen Perea

2. Temática de curso
1. LÓGICA SIMBÓLICA Y LÓGICA PREPOSICIONAL.
1.1. Definiciones y Notaciones.
1.2. Negación, Disyunción, y Conjunción.
1.3. Tablas de Verdad e Interpretación de Fórmulas.
1.4. Implicación y Equivalencia.
1.5. Álgebra Preposicional.
1.6. Validez e Inconsistencia (o Tautologías y Contradicciones)
1.7. Formas Normales
1.8. Consecuencias Lógicas y Prueba de Teoremas
1.9. Aplicaciones de la Lógica Preposicional
2. LÓGICA DE PREDICADOS ( LÓGICA DE PRIMER ORDEN ).
2.1. Definiciones y Notaciones
2.2. Cuantificaciones
2.3. Interpretación de Fórmulas

3. ◦ 3. CONJUNTOS.
◦ 3.1. Definiciones y Notaciones.
◦ 3.2. Los conjuntos N , Z, I, P, Q, R, C, Nm, Zm.
◦ 3.3. Cardinalidad, Conjuntos Finitos e Infinitos, y el Conjunto Vacío
◦ 3.4. Especificaciones de Elementos
◦ 3.5. Subconjuntos y Conjunto Potencia.
◦ 3.6. Subconjunto, Superconjunto, Subconjunto Propio.
◦ 3.7. Conjunto de Conjuntos, Conjunto Potencia
◦ 4. OPERACIONES BÁSICAS.
◦ 4.1. Conjunto Universo, Complemento, Unión, Intersección.
◦ 4.2. Conjuntos Disjuntos, Conjuntos Generados
◦ 4.3. Diagramas de Euler/Venn.
◦ 4.4. Tablas de Membresía

4. ◦ 5. LEYES BÁSICAS DE OPERACIONES SOBRE CONJUNTOS
◦ 5.1. Leyes : Conmutativa, Asociativa, Distributiva, de Identidad, de
◦ Complementos, de Involución, de Indempotencia, de Nulidad, de
◦ Absorción, y de De Morgan.
◦ 5.2. Relaciones
◦ 5.3. Productos Cartesianos.
◦ 5.4. R-Tuplas.

5. ◦ 6. RELACIONES.
◦ 6.1. Relaciones r-arias, binarias.
◦ 6.2. Dominio y Rango.
◦ 6.3. El Opuesto de una Relación.
◦ 6.4. Matriz de Relación.
◦ 6.5. Relación de Identidad.
◦ 6.6. Conceptos Generales de Grafos.
◦ 6.7. Vértices, caminos, bordes, el término alcanzable, descendientes.
◦ 6.8. Composición de las Relaciones.
◦ 6.9. Matrices de Relación de Relaciones Compuestas.
◦ 6.10. Aritmética Booleana : suma y multiplicación.
◦ 6.11. Producto de dos Matrices de Relación
◦ 6.12. Propiedades de las Relaciones.
◦ 6.13. Reflexiva, Simétrica, Asimétrica, Antisimétrica, Transitiva.
◦ 6.14. Relaciones de Equivalencia.

6. ◦ 7. FUNCIONES
◦ 7.1. Definiciones y Notaciones.
◦ 7.2. Valor, Argumento, Dominio, Codominio, Rango.
◦ 7.3. Mapeo/Transformación/Función
◦ 7.4. Restricción, Extensión, Proyección
◦ 8. FUNCIONES INYECTIVAS, SOBREYECTIVAS Y BIYECTIVAS.
◦ 8.1. Composición de Funciones
◦ 8.2. Funciones de Identidad e Inversa
◦ 8.3. Identidad.
◦ 8.4. Inversa Izquierda, Derecha, Ambos Lados
◦ 8.5. Permutaciones.
◦ 8.6. La Permutación Identidad.
◦ 8.7. Ciclos de Orden R
◦ 8.8. Cardinalidad.
◦ 8.9. El Principio del Palomar (Pigeonhole)
◦ 8.10. Conjuntos Enumerables, Contables, e Incontables
◦ 8.11. La Función Característica.
◦ 8.12. Inducción Finita.
◦ 8.13. Ejemplos de Prueba por Inducción

7. Talleres

11. Taller 3
Mapa Conceptual

20. Materiales de estudio para parciales

21. Parciales

22. Adelanto de proyectos

23. Experiencias adquiridas