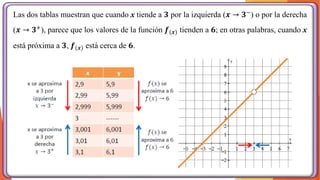
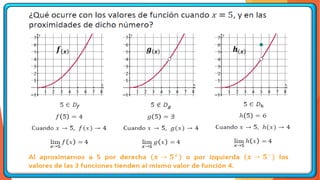
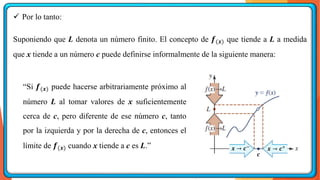
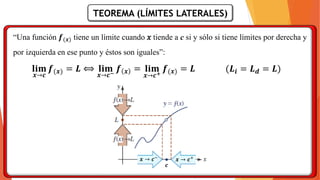
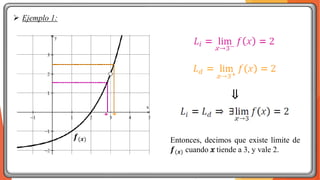
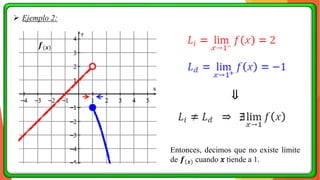
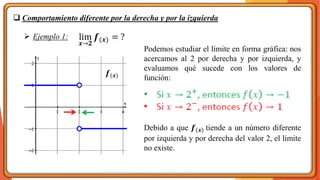
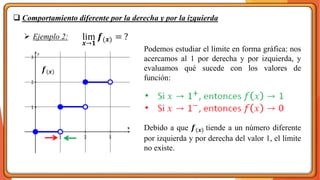
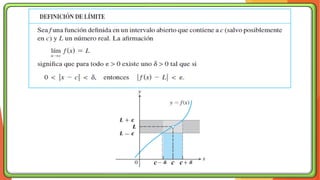
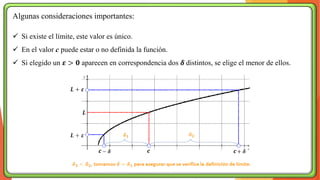
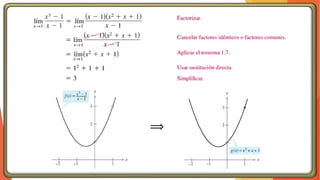
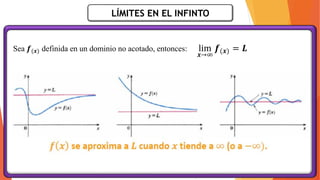
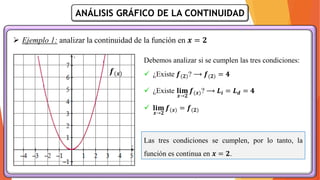
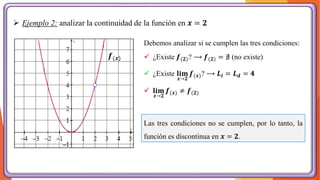
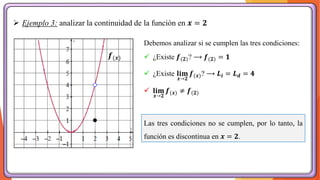
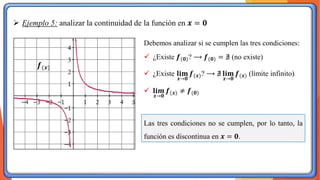
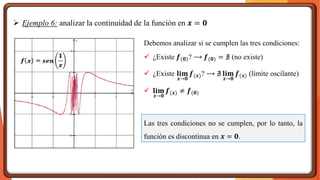
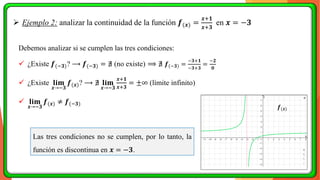
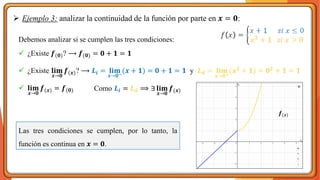
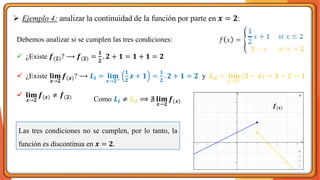
La unidad 2 del análisis matemático se enfoca en los conceptos de límite y continuidad, esenciales para el cálculo. Se exploran los límites de funciones mediante ejemplos y teoremas, destacando su importancia en la determinación de la continuidad de las funciones. La existencia de un límite está ligada a los límites laterales y se presenta una definición formal y propiedades relacionadas.

1. UNIDAD 2: Límite y Continuidad
ANÁLISIS MATEMÁTIC0 2024
LICENCIATURA EN ENOLOGÍA
FCAI - UNCuyo

2. INTRODUCCIÓN AL LÍMITE
• Dentro del estudio del Cálculo, los tres temas más importantes son los conceptos de
límite, derivada e integral.
• Cada uno de estos conceptos está relacionado con las funciones, razón por la cual la
Unidad 1 contiene una revisión de algunos conceptos importantes sobre funciones y sus
gráficas.
• Históricamente, para introducir los enunciados fundamentales del Cálculo se han usado
dos problemas: el de la recta tangente y el del área.

3. Los orígenes del cálculo se remontan a unos 2.500 años a los antiguos griegos, quienes calculaban áreas
usando el “método de agotamiento”. Ellos encontraban el área de cualquier polígono al dividirlo en triángulos
y luego sumaban las áreas de esos triángulos.
Un problema mucho más difícil es encontrar el área encerrada por una figura curvada. El método griego de
agotamiento consistía en inscribir y circunscribir polígonos en la figura curvada y a continuación aumentar el
número de lados de los polígonos.

4. Para el caso anterior del área encerrada por una figura curvada, sea An el área del
polígono inscripto con n lados, a medida que aumenta n, el área An se parece cada
vez más al área del círculo. Así, decimos que el área del círculo es el límite de las
áreas de los polígonos inscriptos, y lo escribimos como:
𝑨 = lim
𝒏→∞
𝑨𝒏
Entonces, el límite de una función es el concepto principal que distingue al Cálculo
del Álgebra y de la Geometría Analítica. Por lo tanto, la noción de un límite es
fundamental para el estudio del Cálculo.

5. LÍMITE (ENFOQUE INFORMAL O INTUITIVO)
❑ Considere la función racional fraccionaria: 𝒇 𝒙 =
𝒙𝟐−𝟗
𝒙−𝟑
• El dominio de esta función es: 𝑫𝒎𝒇 = ℝ − 𝟑
• Esto significa que, aunque no es posible evaluar a la función en el valor 𝟑
(porque al sustituir el 𝟑 en las x se obtiene la indeterminación
𝟎
𝟎
), la función
puede calcularse en cualquier número x que esté muy próximo a 𝟑.

6. Las dos tablas muestran que cuando x tiende a 𝟑 por la izquierda (𝒙 → 𝟑−) o por la derecha
(𝒙 → 𝟑+), parece que los valores de la función 𝒇(𝒙) tienden a 𝟔; en otras palabras, cuando x
está próxima a 𝟑, 𝒇(𝒙) está cerca de 𝟔.

7. ❑ Considere la función racional fraccionaria: 𝒇 𝒙 =
𝟏𝟔−𝒙𝟐
𝟒+𝒙
• El dominio de esta función es: 𝑫𝒎𝒇 = ℝ − −𝟒
• Esto significa que, aunque no es posible evaluar a la función
en el valor −𝟒 (porque al sustituir el −𝟒 en las x se
obtiene la indeterminación
𝟎
𝟎
), la función puede calcularse
en cualquier número x que esté muy próximo a −𝟒 .
Se observa que cuando x tiende a −𝟒 por la izquierda (𝒙 → −𝟒−
) o por la derecha (𝒙 → −𝟒+
),
parece que los valores de la función 𝒇(𝒙) tienden a 𝟖; en otras palabras, cuando x está próxima a
− 𝟒, 𝒇(𝒙) está cerca de 𝟖.

8. 𝒇 𝒙 𝒈 𝒙 𝒉 𝒙

9. ✓ Por lo tanto:
Suponiendo que L denota un número finito. El concepto de 𝒇(𝒙) que tiende a L a medida
que x tiende a un número c puede definirse informalmente de la siguiente manera:
“Si 𝒇(𝒙) puede hacerse arbitrariamente próximo al
número L al tomar valores de x suficientemente
cerca de c, pero diferente de ese número c, tanto
por la izquierda y por la derecha de c, entonces el
límite de 𝒇(𝒙) cuando x tiende a c es L.”
𝒄
𝒙 → 𝒄−
𝒙 → 𝒄+

10. LÍMITES LATERALES
El análisis del concepto de límite se facilita al usar una notación especial. Si el símbolo de
la flecha (→) representa la palabra “tiende”, entonces el simbolismo sería:
▪ Límite por izquierda: 𝒙 → 𝒄− indica que x tiende al número c por la izquierda, es decir,
a través de los números que son menores que c.
▪ Límite por derecha: 𝒙 → 𝒄+ indica que x tiende al número c por la derecha, es decir, a
través de los números que son mayores que c.
▪ Finalmente, la notación 𝒙 → 𝒄 significa que x tiende al número c desde ambos lados, es
decir, por la izquierda y por la derecha de c sobre una recta numérica.

11. ❑ Límite por izquierda:
En general, una función 𝒇(𝒙) puede hacerse arbitrariamente próxima a un número L1 al
tomar x suficientemente cerca, pero sin que sea igual, a un número c por la izquierda;
entonces se escribe:
Se dice que el número L1 es el límite por la izquierda de 𝒇(𝒙) cuando x tiende al número c.
𝒇(𝒙) ⟶ 𝑳𝟏 cuando 𝒙 ⟶ 𝒄−
o bien, 𝐥𝐢𝐦
𝒙→𝒄−
𝒇(𝒙) = 𝑳𝟏

12. ❑ Límite por derecha:
De manera semejante, una función 𝒇(𝒙) puede hacerse arbitrariamente próxima a un
número L2 al tomar x suficientemente cerca, pero sin que sea igual, a un número c por la
derecha; entonces se escribe:
Se dice que el número L2 es el límite por la derecha de 𝒇(𝒙) cuando x tiende al número c.
𝒇(𝒙) ⟶ 𝑳𝟐 cuando 𝒙 ⟶ 𝒄+ o bien, 𝐥𝐢𝐦
𝒙→𝒄+
𝒇(𝒙) = 𝑳𝟐

13. TEOREMA (LÍMITES LATERALES)
“Una función 𝒇(𝒙) tiene un límite cuando 𝑥 tiende a c si y sólo si tiene límites por derecha y
por izquierda en ese punto y éstos son iguales”:
𝒄
𝒙 → 𝒄−
𝒙 → 𝒄+
𝐥𝐢𝐦
𝒙→𝒄
𝒇(𝒙) = 𝑳 ⟺ 𝐥𝐢𝐦
𝒙→𝒄−
𝒇 𝒙 = 𝐥𝐢𝐦
𝒙→𝒄+
𝒇(𝒙) = 𝑳 (𝑳𝒊 = 𝑳𝒅 = 𝑳)

14. ➢ Ejemplo 1:
𝒇(𝒙) Entonces, decimos que existe límite de
𝒇(𝒙) cuando 𝑥 tiende a 3, y vale 2.
⇓

15. ➢ Ejemplo 2:
𝒇(𝒙)
Entonces, decimos que no existe límite
de 𝒇(𝒙) cuando 𝑥 tiende a 1.
⇓

16. EXISTENCIA DEL LÍMITE
“La existencia de un límite de una función 𝒇(𝒙) cuando x tiende a un número c (desde un
lado o desde ambos lados) no depende de si 𝒇(𝒙) está definida en c, sino sólo de si está
definida para valores de x cerca del número c”.

17. ❑ Comportamiento diferente por la derecha y por la izquierda
Podemos estudiar el límite en forma gráfica: nos
acercamos al 2 por derecha y por izquierda, y
evaluamos qué sucede con los valores de
función:
➢ Ejemplo 1:
𝒇(𝒙)
Debido a que 𝒇(𝒙) tiende a un número diferente
por izquierda y por derecha del valor 2, el límite
no existe.
lim
𝒙→𝟐
𝒇(𝒙) = ?

18. ❑ Comportamiento diferente por la derecha y por la izquierda
Podemos estudiar el límite en forma gráfica: nos
acercamos al 1 por derecha y por izquierda, y
evaluamos qué sucede con los valores de
función:
➢ Ejemplo 2:
Debido a que 𝒇(𝒙) tiende a un número diferente
por izquierda y por derecha del valor 1, el límite
no existe.
𝒇(𝒙)
lim
𝒙→𝟏
𝒇(𝒙) = ?

19. ❑ Comportamientos no acotados
Podemos estudiar el límite en forma gráfica: nos
acercamos al -1 por derecha y por izquierda, y
evaluamos qué sucede con los valores de
función:
➢ Ejemplo 1:
Debido a que 𝒇(𝒙) tiende a decrecer sin límite
(−∞) por izquierda y a crecer sin límite por
derecha (+∞) del valor -1, el límite no existe.
𝒇(𝒙)
lim
𝒙→−𝟏
𝒇(𝒙) = ?

20. ❑ Comportamientos no acotados
Podemos estudiar el límite en forma gráfica: nos
acercamos al 3 por derecha y por izquierda, y
evaluamos qué sucede con los valores de
función:
➢ Ejemplo 2:
Debido a que 𝒇(𝒙) tiende a crecer sin límite por
izquierda y por derecha (+∞) del valor 3, el
límite no existe.
lim
𝒙→𝟑
𝒇(𝒙) = ?
𝒇(𝒙)

21. En general, podemos escribir simbólicamente:
lim
𝒙→𝒄
𝒇(𝒙) = ∞ o lim
𝒙→𝒄
𝒇(𝒙) = −∞
Esto no quiere decir que estemos considerando a ∞ o −∞ como un número.
Tampoco significa que el límite exista. Simplemente expresa la forma particular
en que el límite no existe: la función 𝒇(𝒙) puede hacerse tan grande (∞) o tan
chica (−∞) como queramos, tomando a x suficientemente cerca del valor c.
Simbólicamente, lim
𝒙→𝒄
𝒇(𝒙) = ∞ o lim
𝒙→𝒄
𝒇(𝒙) = −∞
sirven para indicar que los valores de 𝒇(𝒙) tienden a ser más y más grandes
(crecen sin límite), o más y más chicos (decrecen sin límite) a medida que x se
acerca más y más al valor c.

22. ❑ Comportamientos oscilantes
Sea 𝒇(𝒙) = 𝒔𝒆𝒏
𝟏
𝒙
, se observa en la figura que,
cuando x se aproxima a 0, 𝒇(𝒙) oscila entre -1 y
1. Por consiguiente, el límite no existe puesto
que, por pequeño que se elija a x, siempre es
posible encontrar valores x1 y x2 donde
𝒔𝒆𝒏
𝟏
𝒙𝟏
= 𝟏 y 𝒔𝒆𝒏
𝟏
𝒙𝟏
= −𝟏, como también
se puede ver en la tabla:
➢ Ejemplo 1: lim
𝒙→𝟎
𝒇(𝒙) = ?

23. DEFINICIÓN FORMAL DE LÍMITE
Si se examina nuevamente la descripción informal de límite: si 𝒇(𝒙) se acerca de manera
arbitraria a un número L a medida que x se aproxima a un valor c por cualquiera de sus
lados, se dice que el límite de 𝒇(𝒙) cuando x se aproxima a c es L, y se escribe:
lim
𝒙→𝒄
𝒇(𝒙) = 𝑳?
A primera vista, esta descripción parece muy técnica. No obstante, es informal porque aún
hay que conferir un significado preciso a las frases: “𝒇(𝒙) se acerca arbitrariamente a L” y
“x se aproxima a c”.

24. En la figura, sea ε la representación de un número positivo (pequeño), entonces, la frase
“𝒇(𝒙) se acerca arbitrariamente a L” significa que 𝒇(𝒙) pertenece al intervalo (L-ε ; L+ε). Al
usar la noción de valor absoluto, esto se puede escribir como 𝒇(𝒙) − 𝑳 < 𝜺.
Del mismo modo, la frase “x se aproxima a c”
significa que existe un número positivo δ tal que x
pertenece al intervalo (c-δ ; c), o bien al intervalo
(a ; c+δ). Esto puede expresarse de manera concisa
mediante la doble desigualdad 𝟎 < 𝒙 − 𝒄 < 𝜹 .
c c
c

25. c c
c

26. Algunas consideraciones importantes:
✓ Si existe el límite, este valor es único.
✓ En el valor c puede estar o no definida la función.
✓ Si elegido un 𝜺 > 𝟎 aparecen en correspondencia dos 𝜹 distintos, se elige el menor de ellos.
𝒄
𝒄 𝒄

27. Ejemplo: determinar δ para un ε dado.

28. PROPIEDADES DE LOS LÍMITES
El límite de 𝒇(𝒙) cuando x se aproxima a c no depende del valor de 𝒇 en 𝒙 = 𝒄 . Sin
embargo, puede darse el caso de que este límite sea 𝒇(𝒄). En esta situación, se puede
evaluar el límite por sustitución directa. Esto es:
lim
𝒙→𝒄
𝒇(𝒙) = 𝒇(𝒄)
Lo que se hace es sustituir al valor de c en la función f, y luego se realizan las operaciones
que correspondan.
Las funciones con este comportamiento son continuas en el valor c.

29. ✓ TEOREMA 1.1

30. ✓ TEOREMA 1.2
( )

32. ✓ TEOREMA 1.3

34. ✓ TEOREMA 1.4
(Funciones Irracionales)
Ejemplos:
▪ lim
𝒙→𝟒
𝒙 = 𝟒 = 𝟐
▪ lim
𝒙→−𝟖
𝟑
𝒙 =
𝟑
−𝟖 = −𝟐
Ejemplos:
▪ lim
𝒙→𝟏𝟔
𝟒
𝒙 =
𝟒
𝟏𝟔 = 𝟐
▪ lim
𝒙→𝟐𝟕
𝟑
𝒙 =
𝟑
𝟐𝟕 = 𝟑

35. ✓ TEOREMA 1.5

37. ✓ TEOREMA 1.6

39. ✓ TEOREMA 1.7
En las diapositivas previas se han estudiado diversos tipos de funciones cuyos límites
pueden calcularse mediante sustitución directa. Lo anterior, aunado al teorema siguiente,
permite desarrollar una estrategia para calcular límites.

41. ⟹

43. LÍMITES EN EL INFINTO
Sea 𝒇(𝒙) definida en un dominio no acotado, entonces: lim
𝒙→∞
𝒇(𝒙) = 𝑳

44. ❑ LÍMITES DE FUNCIONES RACIONALES
Si 𝒇(𝒙) =
𝑷(𝒙)
𝑸(𝒙)
, entonces el lim
𝒙→∞
𝒇(𝒙) nos da una forma indeterminada del tipo
∞
∞
.

45. LÍMITES INFINITOS EN EL INFINTO
Sea 𝒇(𝒙) definida en un dominio no acotado, entonces: lim
𝒙→∞
𝒇(𝒙) = ∞

46. ❑ LÍMITES DE FUNCIONES POLINÓMICAS
Dependiendo del signo del coeficiente principal y del grado del polinomio, tenemos:

47. CONTINUIDAD
Hemos visto que el límite de una función 𝒇(𝒙) cuando x tiende a a, con frecuencia se
obtiene simplemente calculando el valor de la función 𝒇(𝒙) en el valor a, es decir 𝒇(𝒂).
Las funciones con esta propiedad son llamadas continuas en 𝒙 = 𝒂. Veremos que la
definición matemática de continuidad coincide notoriamente con el sentido de continuidad
que la palabra tiene en el lenguaje cotidiano, es decir, un “proceso continuo es uno que se
lleva a cabo gradualmente, sin interrupción o cambio brusco”.

48. Definición de Continuidad:
Una función 𝒇 es continua en un valor 𝒙 = 𝒂 si 𝐥𝐢𝐦
𝒙→𝒂
𝒇(𝒙) = 𝒇(𝒂)
Esta definición es equivalente a que la función 𝒇(𝒙) cumpla las tres condiciones siguientes:
✓ Que exista 𝒇(𝒂), es decir, que 𝒇(𝒂) esté definida (a está en el dominio de f).
✓ Que exista el 𝐥𝐢𝐦
𝒙→𝒂
𝒇(𝒙).
✓ Que 𝐥𝐢𝐦
𝒙→𝒂
𝒇(𝒙) = 𝒇 𝒂 .

49. ANÁLISIS GRÁFICO DE LA CONTINUIDAD
Debemos analizar si se cumplen las tres condiciones:
✓ ¿Existe 𝒇(𝟐)? ⟶ 𝒇(𝟐) = 𝟒
✓ ¿Existe 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙)? ⟶ 𝑳𝒊 = 𝑳𝒅 = 𝟒
✓ 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙) = 𝒇(𝟐)
➢ Ejemplo 1: analizar la continuidad de la función en 𝒙 = 𝟐
Las tres condiciones se cumplen, por lo tanto, la
función es continua en 𝒙 = 𝟐.
𝒇(𝒙)

50. Debemos analizar si se cumplen las tres condiciones:
✓ ¿Existe 𝒇(𝟐)? ⟶ 𝒇(𝟐) = ∄ (no existe)
✓ ¿Existe 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙)? ⟶ 𝑳𝒊 = 𝑳𝒅 = 𝟒
✓ 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙) ≠ 𝒇(𝟐)
➢ Ejemplo 2: analizar la continuidad de la función en 𝒙 = 𝟐
Las tres condiciones no se cumplen, por lo tanto, la
función es discontinua en 𝒙 = 𝟐.
𝒇(𝒙)

51. Debemos analizar si se cumplen las tres condiciones:
✓ ¿Existe 𝒇(𝟐)? ⟶ 𝒇(𝟐) = 𝟏
✓ ¿Existe 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙)? ⟶ 𝑳𝒊 = 𝑳𝒅 = 𝟒
✓ 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙) ≠ 𝒇(𝟐)
➢ Ejemplo 3: analizar la continuidad de la función en 𝒙 = 𝟐
Las tres condiciones no se cumplen, por lo tanto, la
función es discontinua en 𝒙 = 𝟐.
𝒇(𝒙)

52. Debemos analizar si se cumplen las tres condiciones:
✓ ¿Existe 𝒇(𝟏)? ⟶ 𝒇(𝟏) = −𝟏
✓ ¿Existe 𝐥𝐢𝐦
𝒙→𝟏
𝒇(𝒙)? ⟶ 𝑳𝒊 ≠ 𝑳𝒅 ⟹ ∄ 𝐥𝐢𝐦
𝒙→𝟏
𝒇(𝒙)
✓ 𝐥𝐢𝐦
𝒙→𝟏
𝒇(𝒙) ≠ 𝒇(𝟏)
➢ Ejemplo 4: analizar la continuidad de la función en 𝒙 = 𝟏
Las tres condiciones no se cumplen, por lo tanto, la
función es discontinua en 𝒙 = 𝟏.
𝒇(𝒙)

53. Debemos analizar si se cumplen las tres condiciones:
✓ ¿Existe 𝒇(𝟎)? ⟶ 𝒇(𝟎) = ∄ (no existe)
✓ ¿Existe 𝐥𝐢𝐦
𝒙→𝟎
𝒇(𝒙)? ⟶ ∄ 𝐥𝐢𝐦
𝒙→𝟎
𝒇(𝒙) (límite infinito)
✓ 𝐥𝐢𝒎
𝒙→𝟎
𝒇(𝒙) ≠ 𝒇(𝟎)
➢ Ejemplo 5: analizar la continuidad de la función en 𝒙 = 𝟎
Las tres condiciones no se cumplen, por lo tanto, la
función es discontinua en 𝒙 = 𝟎.
𝒇(𝒙)

54. Debemos analizar si se cumplen las tres condiciones:
✓ ¿Existe 𝒇(𝟎)? ⟶ 𝒇(𝟎) = ∄ (no existe)
✓ ¿Existe 𝐥𝐢𝐦
𝒙→𝟎
𝒇(𝒙)? ⟶ ∄ 𝐥𝐢𝐦
𝒙→𝟎
𝒇(𝒙) (límite oscilante)
✓ 𝐥𝐢𝐦
𝒙→𝟎
𝒇(𝒙) ≠ 𝒇(𝟎)
➢ Ejemplo 6: analizar la continuidad de la función en 𝒙 = 𝟎
Las tres condiciones no se cumplen, por lo tanto, la
función es discontinua en 𝒙 = 𝟎.

55. ANÁLISIS ANALÍTICO DE LA CONTINUIDAD
Debemos analizar si se cumplen las tres condiciones:
✓ ¿Existe 𝒇(𝟐)? ⟶ 𝒇(𝟐) = ∄ (no existe) ⟹ ∄ 𝒇(𝟐) =
𝟐𝟐−𝟒
𝟐−𝟐
=
𝟒−𝟒
𝟐−𝟐
=
𝟎
𝟎
✓ ¿Existe 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙)? ⟶ 𝐥𝐢𝐦
𝒙→𝟐
𝒙𝟐−𝟒
𝒙−𝟐
= 𝐥𝐢𝐦
𝒙→𝟐
𝒙+𝟐 𝒙−𝟐
𝒙−𝟐
= 𝐥𝐢𝐦
𝒙→𝟐
(𝒙 + 𝟐) = 𝟐 + 𝟐 = 𝟒
✓ 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙) ≠ 𝒇(𝟐)
➢ Ejemplo 1: analizar la continuidad de la función 𝒇(𝒙) =
𝒙𝟐−𝟒
𝒙−𝟐
en 𝒙 = 𝟐
Las tres condiciones no se cumplen, por lo tanto, la
función es discontinua en 𝒙 = 𝟐.
𝒇(𝒙)

56. ➢ Ejemplo 2: analizar la continuidad de la función 𝒇(𝒙) =
𝒙+𝟏
𝒙+𝟑
en 𝒙 = −𝟑
Debemos analizar si se cumplen las tres condiciones:
✓ ¿Existe 𝒇(−𝟑)? ⟶ 𝒇(−𝟑) = ∄ (no existe) ⟹ ∄ 𝒇(−𝟑) =
−𝟑+𝟏
−𝟑+𝟑
=
−𝟐
𝟎
✓ ¿Existe 𝐥𝐢𝐦
𝒙→−𝟑
𝒇(𝒙)? ⟶ ∄ 𝐥𝐢𝐦
𝒙→−𝟑
𝒙+𝟏
𝒙+𝟑
= ±∞ (límite infinito)
✓ 𝐥𝐢𝐦
𝒙→−𝟑
𝒇(𝒙) ≠ 𝒇(−𝟑)
Las tres condiciones no se cumplen, por lo tanto, la
función es discontinua en 𝒙 = −𝟑.
𝒇(𝒙)

57. ➢ Ejemplo 3: analizar la continuidad de la función por parte en 𝒙 = 𝟎:
Debemos analizar si se cumplen las tres condiciones:
✓ ¿Existe 𝒇(𝟎)? ⟶ 𝒇(𝟎) = 𝟎 + 𝟏 = 𝟏
✓ ¿Existe 𝐥𝐢𝐦
𝒙→𝟎
𝒇(𝒙)? ⟶ 𝑳𝒊 = 𝐥𝐢𝐦
𝒙→𝟎−
(𝒙 + 𝟏) = 𝟎 + 𝟏 = 𝟏 y 𝑳𝒅 = 𝐥𝐢𝐦
𝒙→𝟎+
(𝒙𝟐 + 𝟏) = 𝟎𝟐 + 𝟏 = 𝟏
✓ 𝐥𝐢𝐦
𝒙→𝟎
𝒇(𝒙) = 𝒇(𝟎)
Las tres condiciones se cumplen, por lo tanto, la
función es continua en 𝒙 = 𝟎.
𝒇(𝒙)
Como 𝑳𝒊 = 𝑳𝒅 ⟹ ∃ 𝐥𝐢𝐦
𝒙→𝟎
𝒇(𝒙)

58. ➢ Ejemplo 4: analizar la continuidad de la función por parte en 𝒙 = 𝟐:
Debemos analizar si se cumplen las tres condiciones:
✓ ¿Existe 𝒇(𝟐)? ⟶ 𝒇(𝟐) =
𝟏
𝟐
. 𝟐 + 𝟏 = 𝟏 + 𝟏 = 𝟐
✓ ¿Existe 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙)? ⟶ 𝑳𝒊 = 𝐥𝐢𝐦
𝒙→𝟐−
𝟏
𝟐
𝒙 + 𝟏 =
𝟏
𝟐
. 𝟐 + 𝟏 = 𝟐 y 𝑳𝒅 = 𝐥𝐢𝐦
𝒙→𝟐+
(𝟑 − 𝒙) = 𝟑 − 𝟐 = 𝟏
✓ 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙) ≠ 𝒇(𝟐)
Las tres condiciones no se cumplen, por lo tanto, la
función es discontinua en 𝒙 = 𝟐.
Como 𝑳𝒊 ≠ 𝑳𝒅 ⟹ ∄ 𝐥𝐢𝐦
𝒙→𝟐
𝒇(𝒙)
𝒇(𝒙)