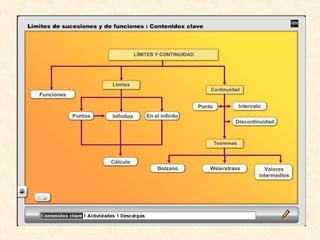
Este documento presenta conceptos básicos sobre límites y continuidad de funciones. Introduce las definiciones de dominio, recorrido y límite de una función en un punto de forma intuitiva y formal. Explica propiedades de los límites como la unicidad y el cálculo de límites simples. Finalmente, clasifica los tipos de indeterminaciones y cómo resolverlas.

1. Límites y continuidad
2º Bachillerato
Presentación elaborada por la profesora Ana Mª Zapatero a partir
de los materiales utilizados en el centro (Editorial SM)

3. Funciones. Primeras definiciones
1.- Dado un nº real “a” y un nº real positivo e, se llama entorno de
centro a y radio e, al intervalo abierto de extremos a - e, a + e:
E(a, e) = (a - e, a + e) = {xÎR/a - e< x < a + e}
2.- 2.1El conjunto A es el dominio de definición.
Dom f = {x/ f(x) es un número real}
2.2. El conjunto de las imágenes de A es el recorrido de la
función.
Rec f = {y / y = f(x) con x del conjunto A}

4. Función real de variable real: ejemplo I
La fórmula f(x)=x 2 relaciona dos variables reales
R
Dominio Recorrido
• 2
• 2,3
• 5
Para que sea aplicación ha de cumplir dos condiciones:
• Todo elemento de D ha de tener imagen.
• Esta imagen ha de ser única.
R
• 4
• 5,29
• 25
f(x) = x2
f(2) = 4
f(2,3) = 5,29
f(5) = 25

5. Función real de variable real: ejemplo II
f(x) • (x, f(x))
x
– 1 1
Dominio
Recorrido
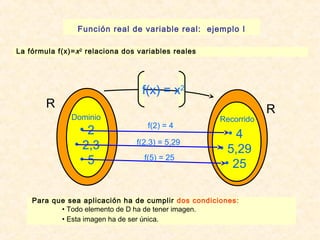
Variable independiente Ley de asociación Variable dependiente
x f y = f(x)
Dominio
D = [–1, 1] f(x) = 1 – x2 Recorrido
f([–1, 1]) = [0, 1]

6. Límite de una función en un punto: definición intuitiva
f(x)
lim
®
Importante: si existe el límite de una función en un punto, dicho límite debe ser un
número y además único.
x 0,98 0,99 0,999 0,9999 1 1,0001 1,001 1,01 1,1
f(x) –1,9412 –1,9703 –1,9970 –1,9997 no existe –2,0003 –2,003 –2,0303 –2,3333
• Cuando x se acerca a 1 por la derecha f(x) se acerca a – 2
• Cuando x se acerca a 1 por la izquierda f(x) se acerca a – 2
Se escribe
lim
x®1
x2 – 1
x2 – 3x + 2 = – 2
Si a y b son dos números, la expresión
x a
=b
quiere decir que si la variable independiente x toma valores próximos al número a,
los correspondientes valores de f(x) se aproximan al número b
Ejemplo: La función f(x) = x2 – 1
x2 – 3x + 2 no está definida en los puntos 1 y 2. ¿Cómo se comporta
cuando x toma valores cada vez más próximos a 1?

7. Límite de una función en un punto: definición formal
Def: Sean a y L dos números reales. Una función f(x) tiene límite L en el punto
x = a si para todo número real e > 0 existe otro número real d > 0, tal que si
0 < |x – a | < d Þ |f(x) – L | < e
Para cada e > 0 Hay un d> 0 0 < |x – a | <d |f(x) – L | < e
La condición 0 < | x – a | < d prohibe que x tome el valor a.
No es necesario que la función esté definida en a.

8. Límites laterales de una función
· Se dice que el número b es el límite de f(x) cuando x tiende hacia a por la dere-cha
(izquierda) , si al tomar valores x estrictamente mayores (menores) próximos
al número a, los correspondientes valores de f(x) se aproximan al número b. Se
designa
(lim f (x)= b).
Ejemplo: la función Ent(x) = «mayor nº entero menor o igual a x» tiene una gráfica como
la siguiente. Se observa que:
·
lxi®m3 + Ent(x) = 3
·
lxi®m3 – Ent(x) = 2
Como los límites laterales no coinciden la
función no tiene límite cuando x®3.
3
x®alim + f (x) = b (
x®a –
· Una función se dice que tiene límite en un punto si y sólo si existen los límites
laterales y ambos son iguales.

9. Teorema de la unicidad del límite
Enunciado: Si una función tiene límite en un punto, es único.
Demostración: La demostración se hace por reducción al absurdo
Suponemos que f(x) tiene 2 límites distintos b y c, si x tiende a “a”. Y b > c.
limx->af(x)=b => (por def. de límite) " E(b, e) $ d1 ' "x Î E*(a,d1) f(x) ÎE(b, e)
limx->af(x)=c => (por def. de límite) " E(c, e) $ d2 ' " x Î E*(a, d2) f(x) Î E(c, e)
Consideremos un ε tal que E(b, e)∩ E(c, e) = Ø.
Por ej. c+ε < b-ε => ε < (b - c)/2 y sea δ = min {d1 , d2}
Para todo x perteneciente al E*(a, δ ) se cumple
 f(x) pertenece a E(b, e)
 f(x) pertenece a E(c, e)
Absurdo, pues f(x) no puede pertenecer a dos entornos disjuntos. El absurdo
procede de suponer b ≠ c. Por lo tanto b = c.

10. Propiedades de los límites de funciones
2. Si k es un número real lim(k · f(x)) = k · lim f(x) = k · p

11. Propiedades de los límites. Demostración
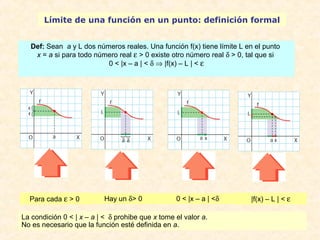
Enunciado: El límite de una suma es igual a la suma de los límites (si
son finitos)
Demostración: Queremos probar que, dado ε > 0, $ δ > 0 ' " x Î E(a, δ)
f(x)+g(x) Î E(b+c, ε ). Es decir |(f(x) + g(x)) - (b+c)| < ε.
Sea ε' = ε/2
lim
f(x)=b => (def. de lím.) " ε'>0 $ δ1>0 ' " x Î E(a,δ1) |f(x) - b| < ε'.
x®a
lim
g(x)=c => (def. de lím.) " ε'>0 $ δ2>0 ' " x Î E(a,δ2) |g(x) - c| < ε'.
Sea δ = min {δ1,δ2}. " x Î E(a,δ) se cumple:|f(x) - b| < ε‘, |g(x) - c|< ε‘
=> |f(x) - b| + |g(x) - c| < 2ε' = ε
|(f(x) + g(x)) - (b+c)|=|(f(x) - b) + (g(x) - c)|£ |f(x) - b|+|g(x) - c| < ε
(*) Desigualdad triangular: |a + b| ≤ |a| + |b|
lim
=> (por def. de límite) [f(x) + g(x)] = b + c
x®a
x®a

12. Límites infinitos de una función en un punto: definición
• Se dice que el límite de f(x) cuando x tiende hacia el punto “a” es mas infinito si la
función f(x) se hace tan grande como se quiera (en valor absoluto) siempre que se
tomen valores de x suficientemente próximos al número a, pero distintos de él. Se
designa :
= +¥
lim f (x)
x a
•· Se dice que el límite de f(x) cuando x tiende hacia el punto “a” es menos infinito si
la función f(x) se hace tan grande como se quiera (en valor absoluto) siempre que se
tomen valores de x suficientemente próximos al número a, pero distintos de él. Se
designa:
lim f (x)
x a
Ejemplo: observando la gráfica de la
función f(x) = 1
·
x®0+ lim
| x | se ve que:
1
| x | = ¥
·
x®0– lim
1
| x | = ¥
lim
Û
1
| x | = ¥
x®0
®
= -¥
®

13. Límite infinito en un punto: definición formal
Ejemplo: En la medida en que x se acerca o 0, con valores positivos ¿a quién se acerca
f(x) = (x+1) / x?
x 1 0,1 0,01 0,01 ®0+
f(x) = (x+1)/x 2 11 101 1001 ®+¥
x + 1
x = +¥
x®0+ lim
De igual manera si x se acerca a 0 con valores negativos se ve que:
x + 1
x = –¥
x®0– lim
• El límite de f(x) cuando x tiende a “a” por la derecha es infinito si para cada
número K > 0 existe otro número d > 0 tal que f(x) > K si a < x < a + d donde d
es función del K elegido .
• El límite de f(x) cuando x tiende a “a” por la izquierda es menos infinito si para
cada número K < 0 existe otro número d > 0 tal que f(x) < K si a – d < x < a donde
d debe ser función de K.

14. Límites finitos en el infinito: Definición
Se dice que el nº L es el límite de f(x) cuando x tiende a infinito (menos infinito), si
la distancia | f(x) – L | se hace tan pequeña como se quiera siempre que se tomen
valores de x suficientemente grandes (en valor absoluto). De denota
f x L
lim ( )
x
=
®+¥
lim ( )
Ejemplo (comportamiento en el infinito, límite finito) : En la medida en que x
se hace muy grande, con valores positivos ¿a quién se acerca f(x) = (x+1) / x?
x 10 102 103 104 ®+ ¥
f(x) = (x+1)/x 1,1 1,01 1,001 1,0001 ®1
lim
x + 1
x = 1
x®+¥
f x L
x
=
®-¥

15. Límites infinitos en el infinito: Definición
Def: El límite de f(x) cuando x tiende a infinito es infinito si para todo número real M
se puede encontrar otro número real K tal que f(x) > M si x > K donde K debe ser
función de M.
En la medida en que x se hace muy grande, con valores positivos ¿a quién se acerca
f(x) = x2 ?
x 10 102 103 104 ® + ¥
f(x) = x2 102 104 106 108 ® + ¥
lim x2 = + ¥
x® + ¥
Otros comportamientos en el infinito, gráficamente.

16. Ejemplo de comportamiento en el infinito: no existe límite
Cuando x tiende a infinito o x tiende a menos infinito los valores de estas
funciones seno y coseno no tienden a ningún valor, ya que oscilan entre 1 y –1.
Ambos límites no existen.

17. Cálculo de límites
Límites simples
lim f (x) f (a)
x a
Cuando las funciones verifican se pueden obtener directamente
por el procedimiento de sustituir en la expresión de la función el valor de la variable x
por el de a hacia el que tiende.
Algunos límites típicos
lim x = 1
x
·
lim è ç ç æ ø ÷ ÷ ö
x®¥
1 +
ax
= ea, para todo a
=
®
sen x ·
x®0
x
lim ex
·
x®¥
p = ¥, para todo p
lim
ln x ·
x®¥
xp = 0, para todo p > 0

18. Cálculo de límites simples: ejemplos
lim
x®0
x2 cos x + e2x
ln (x + 1) + x3 + 1 =
0 . 1 + e0
ln 1 + 0 + 1 = 1
lim
ç è lim x®1
æ
ç x3 + x – 1
x2 – 1 = –100 + 1 = – 99
ø ÷ ÷ ö
è ç ç æ
3 2x3 – 2x + 1
x3 –x + 1
(x2 – 2x + 1)
= è ç ç æ
ø ÷ ÷ ö
3 2 . 13–2 . 1 + 1
13 – 1 + 1
(12–2.1+1)
= 10 = 1
lim
x®3
–2x2 + 3
x3 – 2x + 5 =
–2 . 32 + 3
33 – 2 . 3 + 5 = –
15
16
x®0
ø ÷ ÷ ö x2 – 100 +

19. Indeterminaciones: tipos
Cuando podemos calcular el límite de la operación de dos o más funciones, aun sin
conocerlas, decimos que el límite es determinado. Aplicando las propiedades de los
límites podemos obtener el límite buscado. En caso de que no podamos aplicar ninguna
propiedad que nos permita calcular el límite, diremos que es indeterminado.
lim f(x) = 2
lim g(x) = 3
lim
Este resultado no depende de las funciones f
y g. El límite es determinado.
lim f(x) = 0
lim g(x) = 0
No es posible obtener
lim
Este límite depende de las funciones f y g. El
límite es indeterminado.
x®a
x®a
Entonces
x®a
f(x)
g(x) =
23
x®a
x®a
x®a
f(x)
g(x) . Para
poder salvar la indeterminación hemos
de conocer f y g.
Tipos de
indeterminacione s
L0
/ L ¹ 0 00
¥¥
0 . ¥ ¥ – ¥ ¥0 00 1¥

20. Cuadro de indeterminaciones: Forma de resolverlas
Tipos de
indeterminacione s
L0
/ L ¹ 0 00
¥¥
0 . ¥ ¥ – ¥ ¥0 00 1¥
•En las del tipo L/0 con L no nulo, se calculan los límites laterales
•En las del tipo 0/0 Si hay raíces, se multiplica por el conjugado de la expresión con
raíces y luego se factoriza y simplifica
• Si no hay raíces, se factoriza y simplifica
¥
•En las del tipo Se dividen numerador y denominador por la máxima potencia
¥
¥· 0
¥ -¥
•En las del tipo Se transforman, mediante operaciones, en uno de los anteriores
•En las del tipo
•Si no hay radicales se hacen operaciones y se transforma en uno de los anteriores
•Si hay radicales, se multiplica y se divide por el conjugado y se transforma en uno
del tipo
¥0 ,00 y1¥
•En las de los tipos Se aplican logaritmos o la expresión correspondiente

21. Ejemplos de cálculo de indeterminaciones: tipo L/0, con L ¹ 0
En estos casos el límite si existe es +¥ o –¥ dependiendo del signo de la función
a izquierda y derecha del valor al cual tiende la variable.
lim
1
x – 2 = – ¥
·
x®2–
lim
1
x – 2 = + ¥
·
x®2+
lim
1
x – 2 no existe
Þ
x®2
lim
1
(x – 2)2 = + ¥
·
x®2–
lim
1
(x – 2)2 = + ¥
·
x®2+
lim
Þ
1
(x – 2)2 = + ¥
x®2

22. Ejemplos de cálculo de indeterminaciones: tipo 0/0
Cuando el
lim
x®a
P(x)
Q(x) es indeterminado
00
siendo P(x) y Q(x) polinomios, pod e-mos
salvar la indeterminación dividiéndolos ambos por (x – a)
lim
–18 + 21x – 8x2 + x3
·
x®3
x2 – 9 =
lim
(x – 3)2(x – 2)
(x – 3)(x + 3) =
x®3
lim
(x – 3)(x – 2)
(x + 3) = 06
x®3
= 0
Indet 00
lim –18 + 33 x – 20 x2 + 4 x3
·
x®32
9 – 12 x + 4 x2 =
lim (x – 2)(2x – 3)2
x®32
(2x – 3)2 =
lim (x – 2) = –1
x®32
2
Indet 00

23. Ejemplo de cálculo de indeterminaciones: tipo 0 . ¥
Estas indeterminaciones se resuelven a veces operando previamente para
obtener una expresión más sencilla o reduciéndolas a otras del tipo
lim xpe–x = 0
lim x3e–x + lim x2e–x +
7
= 0 + 5 . 0 + 7 . 0 = 0
lim ln
®¥ = 0
1/x = y
00
o
¥¥
Recordando que
x®¥
·
x®¥ lim (x3 + 5x2 + 7x)e–x =
Indet 0 . ¥
Recordando que x
x
X
·
x®0+ lim x . ln x =
x®0+ lim ln x
1x
= lim
0
y®¥
– ln y
y =
5
x®¥
x®¥
x®¥ lim xe–x =
Indet 0 . ¥

24. Ejemplos de cálculo de indeterminaciones: tipo ¥/¥
lim
lim –2x3 + 3x – 5
lim
En otros casos un cambio de variable permite salvar la indeterminación.
lim
ln x = y
x®¥
–x3 – 2x + 5 =
Indet
¥¥
x®¥
–2 +
3
x2 –
5
x3
–1 –
2
x2 +
5
x3
= –2
–1 = 2
lim
x®¥
ln (ln x)
ln x =
y®¥
ln y
y = 0
Indet
¥¥
Cuando el
x®¥
P(x)
Q(x) es indeterminado
¥¥
siendo P(x) y Q(x) polinomios,
podemos salvar la indeterminación dividiéndolos ambos por la potencia más
alta de x que aparezca en ambos.

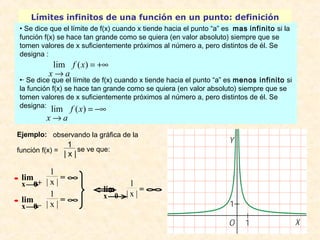
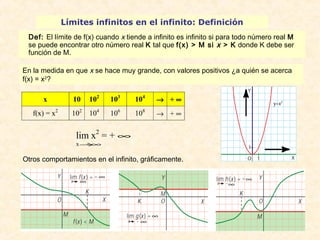
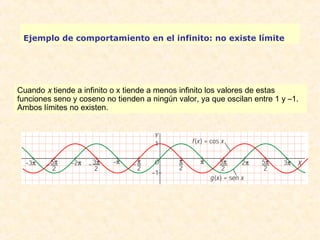
25. Ejemplos de cálculo de indeterminaciones: tipo ¥ – ¥
En estos casos es aconsejable operar previamente para simplificar, si es posible, la
expresión antes de tomar el límite.
Cuando la indeterminación procede de una diferencia de radicales, es conveniente multi-plicar
y dividir por la expresión conjugada .
lim (x3 – x2) =
x®¥
Indet ¥ – ¥
lim x2(x – 1) = ¥ . ¥ = ¥
x®¥
lim [ x2 + 1 – x2 – 1] =
x®¥
Indet ¥ – ¥
lim
[ x2 + 1 – x2 – 1] [ x2 + 1+ x2 – 1]
x®¥
[ x2 + 1+ x2 – 1] =
=
lim
x®¥
(x2 + 1) – (x2 – 1)
[ x2 + 1 + x2 – 1] =
lim
x®¥
2
x2 + 1 + x2 – 1 = 2
¥ = 0

26. Ejemplos de cálculo de indeterminaciones: tipos ¥0, 00
Estas indeterminaciones se resuelven frecuentemente tomando logaritmos y
expresando la función inicial como «la exponencial de su logaritmo».
x ®+¥
Indet 0
e0 = 1
x
x
ln
lim 0 1
= = =
x
e e
®+¥
x®0+ lim xx =
Indet 0 0
x®0+ lim eln (xx ) =
x®0+ lim ex ln x =
( )1
lim x
x
1
lim e ln xx
x
®+¥
=

27. Ejemplos de cálculo de indeterminaciones: tipo 1¥
Para resolver estas indeterminaciones resulta útil muchas veces recordar la expresión
de ea como límite, combinada con un cambio de variable.
lim è ç ç æ
Indet 1¥
lim (1 + 2x2 + x4)
Indet 1¥
1
2x2 + x4 = y
e8
x®¥
ø ÷ ÷ ö
1 +
1x
lim è ç ç æ
2x
=
x®¥
ø ÷ ÷ ö
è ç æ
ø ÷ ö
1+
1
x
x 2
=
è ç ç æ
ø ÷ ÷ ö
lim è ç æ
x®¥
ø ÷ ö
1+
1
x
x 2
= e2
x®0
4
x2
= lim
x®0
è ç æ
ø ÷ ö
1 +
11
2x2 + x4
4
x2
=
lim
x®0
è ç ç æ
ø ÷ ÷ ö
è ç æ
ø ÷ ö
1 +
11
2x2 + x4
1
2x2 + x4 (2x2 + x4 ) 4
x2
=
lim ë ê é
=
y®¥
û ú ù
è ç æ
ø ÷ ö
1 +
1
y
y
lim 4(2x2 + x4 )
x®0
x2
lim ë ê é
=
y®¥
û ú ù
è ç æ
ø ÷ ö
1 +
1
y
y
lim (8 + 4x2)
x®0
=

28. Continuidad en un punto: primera aproximación
Estatura medida cada 5 años:
hay grandes saltos entre cada
punto y el siguiente.
Estatura medida cada año: el
incremento entre cada punto y el
siguiente será menor, como lo es
también el incremento de tiempo.
Una función es continua cuando a pequeñas variaciones de la variable
independiente le corresponden pequeñas variaciones de la variable
dependiente.

29. Continuidad en un punto: definición
lim [f(a + h) – f(a)] = 0
Al hacer a + h = x, si h®0
entonces x®a
lim f(x) = f(a)
Desglosando la
definición de límite
Al llamar f(a + h) – f(a) = Dy, si Dx =
h®0 entonces Dy ®0
Una función f(x), definida en x = a, es continua
en dicho punto cuando:
h® 0
Una función f(x), definida en x = a, es continua
en dicho punto cuando:
x® a
Una función f(x), definida en x = a, es continua
en dicho punto cuando:
lim Dy =0
Dx® 0
Una función f(x), definida en x = a, es continua en
dicho punto cuando:
· Existe
lim f(x)
x® a
· Existe f(a)
· Los dos valores anteriores son iguales

30. Continuidad en un punto: definición formal
Una función f(x) tiene límite L en el punto x = a si
"e (real) >0 $ d>0, ' si:
0 < |x – a | < d Þ |f(x) – L | < e
lim f(x) = f(a)
Definición formal continuidad
Una función f(x), definida en x=a, es continua en
dicho punto si "e (real) >0 $ d>0, ' si:
|x – a | < d Þ |f(x) – f(a) | < e
Usando la definición de
continuidad Usando la
definición formal
de límite
Una función f(x), definida en x = a, es continua
en dicho punto cuando:
x® a

31. Continuidad en un intervalo: definición
Una función f(x) es continua en a por la derecha
si y sólo si
x® a + lim f (x ) = f(a)
Una función f(x) es continua en a por la izq uierda
si y sólo si
x® a – lim f(x) = f(a)
• Una función es continua en un intervalo abierto (a, b) si es continua en cada uno de sus puntos.
• Una función es continua en un intervalo cerrado [a, b] si es continua en cada uno de los puntos
del intervalo (a, b), y además es continua en a por la derecha y en b por la izquierda.
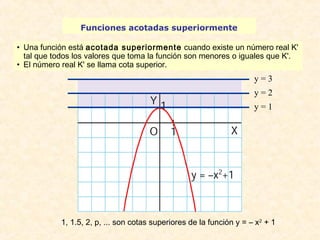
f(x) = 1 – x2 es continua en
[–1, 1], pero no es continua ni
en 1 ni en –1 porque no lo es
por la derecha o por la i zquierda.
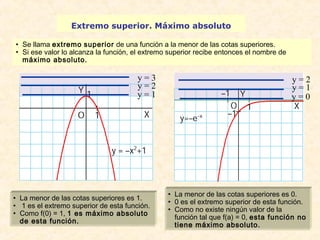
f(x) =
1x
no es continua en
[–1, 1], porque no está
definida en 0.
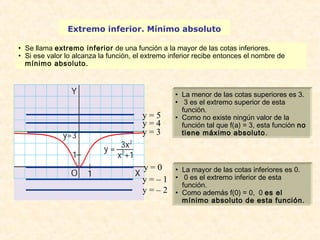
f(x) =
x 2 si x < 1
2 si x ³ 1
îï í ï ì
no es
continua en [ –1, 1], porque no
es continua por la izquierda
en 1.

32. 3
Función discontinua en un punto
Cuando una función no cumple la definición de función continua en un punto se dice
que es discontinua.
Estas funciones no son
continuas en el punto 1
Esta función no es
continua en los puntos 1
y – 1
Función discontinua en 0
4

33. Discontinuidad evitable
Una función tiene una discontinuidad evitable en un punto cuando existe límite en él y
no coincide con el valor de la función en el mismo.
f(x) =
x2 – 1
x – 1 si x ¹ 1
3 si x = 1
î ï í ï ì
Estudiamos el comportamiento de f(x) en el punto 1:
Por tanto f(x) presenta una discontinuidad evitable en el punto 1.

34. Evitando una discontinuidad evitable
El valor que deberíamos dar a una función en un punto (en el que la función
presenta discontinuidad evitable) para que dicha función sea continua es el
verdadero valor de la función en el punto.
La siguiente función g(x), evita la discontinuidad que presenta f(x) en el punto 1:
g(x) =
x2 – 1
x – 1 si x ¹ 1
2 si x = 1
î ï í ï ì
=
• El verdadero valor de f(x) en el
punto 1 es 2.
• La función g(x) es continua en
el punto 1.
î ï í ï ì(x – 1)( x + 1)
x – 1 si x ¹ 1
2 si x = 1
= x + 1

35. Discontinuidad inevitable
• Una función tiene en un punto una discontinuidad inevitable cuando existen
los límites laterales en él y son distintos.
• Si f(x) es discontinua en el punto x = a, la diferencia entre los dos límites se
llama salto de la función en dicho punto.
• Si alguno de los límites laterales en el punto a son infinito, se dice que el salto
y = sig(x) presenta discontinuidad
inevitable en el punto 0 de salto 2.
y =
î ï í ïìx + 1
x si x ¹ 0
0 si x = 0
y = sig(x)
Esta función presenta discontinuidad
inevitable de salto infinito en el punto 0.
es infinito

36. Funciones acotadas superiormente
• Una función está acotada superiormente cuando existe un número real K'
tal que todos los valores que toma la función son menores o iguales que K'.
• El número real K' se llama cota superior.
y = 3
y = 2
y = 1
1, 1.5, 2, p, ... son cotas superiores de la función y = – x2 + 1

37. Función acotada inferiormente
• Una función está acotada inferiormente cuando existe un número real K tal
que todos los valores que toma la función son mayores o iguales que K.
• El número real K se llama cota inferior.
y = 0
y = – 1
y = – 2
0, –1, –1.5, –p, .... son cotas inferiores de la función y = e– x

38. Extremo superior. Máximo absoluto
• Se llama extremo superior de una función a la menor de las cotas superiores.
• Si ese valor lo alcanza la función, el extremo superior recibe entonces el nombre de
máximo absoluto.
y = 3
y = 2
• La menor de las cotas superiores es 1.
• 1 es el extremo superior de esta función.
• Como f(0) = 1, 1 es máximo absoluto
de esta función.
y = 2
y = 1
• La menor de las cotas superiores es 0.
• 0 es el extremo superior de esta función.
• Como no existe ningún valor de la
función tal que f(a) = 0, esta función no
tiene máximo absoluto.
y = 1
y = 0

39. Extremo inferior. Mínimo absoluto
• Se llama extremo inferior de una función a la mayor de las cotas inferiores.
• Si ese valor lo alcanza la función, el extremo inferior recibe entonces el nombre de
mínimo absoluto.
• La menor de las cotas superiores es 3.
• 3 es el extremo superior de esta
función.
• Como no existe ningún valor de la
función tal que f(a) = 3, esta función no
tiene máximo absoluto.
• La mayor de las cotas inferiores es 0.
• 0 es el extremo inferior de esta
función.
• Como además f(0) = 0, 0 es el
mínimo absoluto de esta función.
y = 5
y = 4
y = 3
y = 0
y = – 1
y = – 2

40. Teorema de acotación
Enunciado: Si una función tiene límite finito en un punto “a”, está acotada
en un entorno reducido de “a”
Demostración:
(por def. de límite)
f x b
lim ( )
x a
=
®
" e>0 existe δ>0 ' "x ÎE*(a, δ) f(x) ÎE( b, e )
lo que indica b - ε < f(x) < b + ε
--^-- --^--
h k
cota inferior cota superior
Nota: también podemos expresar la tesis como
" e>0 $ δ>0 y $ h y k reales positivos ' " x ÎE*(a, δ)
h < |f(x)| < k.
Luego la función f(x) está acotada

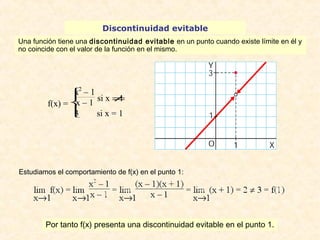
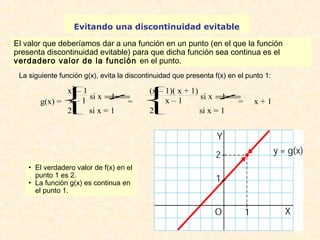
41. Teorema de Bolzano: Enunciado e interpretación geométrica
Sea f(x) una función continua en un intervalo cerrado [a, b], que toma en a y
b valores de signo opuesto (es decir f(a) · f(b) < 0), entonces $ al menos un
punto c interior al intervalo en el que f(c) = 0.
c
f(x) continua en [a, b]
f(a) < 0
f(b) > 0
Entonces $ c Î (a, b) ' f(c) = 0
c
f(x) continua en [a, b]
f(a) > 0
f(b) < 0
Entonces $ c Î (a, b) ' f(c) = 0

42. Teorema de Bolzano: Demostración (I)
 Supongamos que f(a)<0 y f(b)>0. (La demostración sería análoga si supusiéramos
f(a)>0 y f(b)<0.)
 Consideremos el punto medio de [a,b]: (a+b)/2.
 Si f((a+b)/2)=0 queda demostrado el teorema.
Si no, f será positiva o negativa en (a+b)/2.
Tomemos una de las mitades del intervalo [a,b] donde la función sea negativa en un
extremo y positiva en el otro. Llamemos a1 y b1 a los extremos de este intervalo.
Ahora dividamos [a1,b1] a la mitad.
Si f no vale cero en el punto medio, será positiva o negativa. Tomemos la mitad
donde f tiene distinto signo en cada extremo, y llamemos a estos puntos a2 y b2.
 Si continuamos de esta manera, obtenemos una sucesión de intervalos [a,b], [a1,b1],
[a2,b2], etc., tales que
a £ a1 £ a2 £...£ an y b ³ b1 ³ b2 ³...³ bn.
Es decir,
1) Los aI forman una sucesión creciente y los bI forman una sucesión decreciente.
2) Los aI son siempre menores que los bI.

43. Teorema de Bolzano: Demostración (II)
b - a
lim( ) n n n
Veamos cuál es el
La long. del intervalo [a1,b1] es,(b-a)/2 , la mitad de la long. de [a,b] que es b - a.
La longitud del intervalo [a2,b2] es (b - a)/22, la mitad de la longitud de [a1,b1] que
es (b - a)/2.
®¥
Y siguiendo de esta manera, la longitud del intervalo [a,b] es (b - a)/2n.
nn3) De modo que,
lim( b - a ) = lim b - a
=
n®¥ n n n®¥ 2
n
1), 2) y 3) son las condiciones que permiten obtener un único número frontera entre
ambas sucesiones y que esté en todos los intervalos.
$ c ' "n an £ c £ bn,
0
Esto significa que, para cualquier entorno de c que consideremos, $ un intervalo
[an,bn] contenido en dicho entorno.
Es decir, para todo δ>0 $ n1 / para todo n >= n1 c-δ < [an,bn] < c+δ.

44. Teorema de Bolzano: Demostración (III)
Por otro lado, f es continua en [a,b] por hipótesis. Por lo tanto es continua en c.
Por definición de continuidad, lim
f(x)=f(c).
x®c
Vamos a proceder por reducción al absurdo
Supongamos que f(c)<0, por teo. de conservación del signo $ un entorno de c
donde f(x) es negativa.
Dentro de este entorno, $ un intervalo [a,b], donde f(a) es de distinto signo
nnnque f(b).
nEsto es una contradicción, por lo tanto f(c) no puede ser negativo.
Si f(c)>0, por teo. de conservación del signo $ un entorno de c donde f(x) es
positiva.
Pero, otra vez, dentro de ese entorno existe un intervalo [an,bn] tal que f(an)
es de distinto signo que f(bn).
Esto es una contradicción, por lo tanto f(c) no puede ser positivo.
Por lo tanto, no existe otra posibilidad: f(c)=0.

45. Teorema del máximo – mínimo. Teorema de
Weierstrass
Enunciado e interpretación geométrica
Enunciado: Toda función continua en un intervalo cerrado [a, b], alcanza en dicho
intervalo al menos un máximo absoluto y un mínimo absoluto.
x1
M
x2
m
Esta función, continua en [a, b], presenta en
x1 un máximo absoluto de valor M y en x2
un mínimo absoluto de valor m.
x1
M
x2
m
Esta función, continua en [a, b], presenta en
x1 un máximo absoluto de valor M y en x2
un mínimo absoluto de valor m.

46. Teorema del máximo – mínimo. Teorema de Weierstrass
Demostración (I)
Se hace la demostración en dos partes
A) La función está acotada en [a,b].
Lo haremos por reducción al absurdo. Supongamos que f no está acotada, Si
tomamos x0 el punto intermedio del intervalo, la función no estará acotada en
[a,x0] o en [x0,b].
Elegimos de los dos aquel en el que no está acotada y reiteramos el proceso
obteniendo así un sucesión de intervalos cerrados encajados y tales que la
amplitud tiende a cero. Luego existe un nº real c del intervalo (a,b) que
pertenece a todos ellos y por tanto f( c ) no está acotada.
Sin embargo, f es continua en todo el intervalo y c está en él, luego es continua
en c y por el teorema de acotación f( c ) está acotada, lo que lleva a una
contradicción.
Por tanto la suposición que hemos hecho no es válida y por ello la función f está
acotada en todo el intervalo

47. Teorema del máximo – mínimo. Teorema de Weierstrass
Demostración (II)
B) Por el apartado A) existen un éxtremo inferior m y un extremo superior M.
Si M es un valor de la función ya estaría demostrado.
En caso contrario M-f(x) es distinto de cero.
Construimos la función g ( x
) =
1
M f x
que está definida y es continua en [a,b].
-
( )
Por el apartado A) esta función está acotada, luego existe un nº K tal que
g x ( ) 1
K
( ) 1 < K Þ f x < M
-
M f x
( )
-
=
Y esto es cierto para todo x del dominio. Por lo que hemos encontrado una cota
menor que el extremo superior lo que indica una contradicción.
Esta procede de suponer que M – f (x) es no nulo luego M = f(x) por lo que M es
máximo.

48. Teorema de los valores intermedios o de Darboux
Enunciado e interpretación geométrica
Sea f(x) una función continua en un intervalo cerrado [a, b] y K un número
real tal que:
f(a)< K <f(b) o f(b)< K <f(a),
entonces existe al menos un punto c en el intervalo tal que f(c) = K.
f(x) continua en [a, b]
f(a) < K< f(b)
Entonces $ c Î (a, b) / f(c) = M
f(x) continua en [a, b]
f(b) < K< f(a)
Entonces $ c Î (a, b) / f(c) = M
c
K
c
K
La demostración se hace comprobando que la función g(x) = f(x) – K cumple el
teorema de Bolzano luego g(c) = 0 por lo que f( c) = K