Este documento define los conceptos básicos de límites de funciones. Explica que un límite es el valor al que se aproxima una función cuando la variable independiente se aproxima a un punto. Define límites laterales, límites finitos e infinitos, y cómo calcular límites de funciones elementales y compuestas mediante propiedades de operaciones con límites. También describe cómo resolver indeterminaciones que surgen al calcular ciertos límites.

1. LÍMITES DE FUNCIONES
1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO
Intuitivamente la idea que tenemos de límite de una función en un punto es el número hacia
el que se aproximan los valores que toma la función cuando la variable independiente se
aproxima a ese punto.
Analíticamente podemos definir el límite de una función en un punto de la siguiente manera:
Una función f tiene por límite L cuando x tiende a a si para todo entorno E(L ,e)
existe un entorno E(a ,d) , de modo que para todo x perteneciente al entorno reducido
E* (a ,d) se cumple que f (x) pertenece al entorno E(L ,e)
lim f ( x) = L Û " e > 0, $ d > 0 / " x Î E(a ,d ) Þ f ( x) Î
E( L , e )
x ®
a
Por la definición de entorno podemos expresar la definición de límite de la siguiente
manera:
Una función f tiene por límite L cuando x tiende a a si para todo e > 0 , existe un
d > 0 tal que si 0 < x -a <d , entonces f (x)-L <e
( ) = Û "e > $d > < - < d Þ ( ) - < e
lim 0, 0 / 0
®
f x L x a f x L
x a
Si una función f (x) cumple esta definición, decimos que es convergente en a .
Nota: Para que una función tenga límite en un punto de abscisa a , o sea convergente en ese
punto, no es necesario que la función esté definida en ese punto.
Cálculo analítico de algunos límites

2. En las funciones elementales definidas por una sola fórmula (funciones polinómicas,
racionales, irracionales, exponenciales, logarítmicas y trigonométricas) se tiene que:
f ( x) f (a)
lim siempre que aÎDom f
x a
=
®
2. LÍMITES LATERALES
Existen funciones en las cuales no es posible calcular directamente el límite en algún punto.
Esto es debido a que estas funciones están definidas de diferente manera a la izquierda y a la
derecha de ese punto. Para estudiar estos límites, necesitamos recurrir a los límites laterales.
Una función f tiene por límite L cuando x tiende a a por la izquierda si para todo
e > 0 , existe un d > 0 tal que si a -d < x < a , entonces f (x)-L <e . Se escribe
f ( x) L
= ® -
lim .
x a
Una función f tiene por límite L cuando x tiende a a por la derecha si para todo
e > 0 , existe un d > 0 tal que si a < x < a +d , entonces f (x)-L <e . Se escribe f ( x) L
= ® +
lim
x a
.
CONDICIÓN NECESARIA Y SUFICIENTE DE CONVERGENCIA
La condición necesaria y suficiente para que una función f tenga límite en un punto de
abscisa a es que tenga límite lateral por la izquierda, tenga límite lateral por la derecha y ambos
sean iguales.
f ( x) L f ( x) f ( x) L
= Û = = ® ® - ® +
lim lim lim
x a x a x a
Cálculo analítico de algunos límites
Cuando necesitamos calcular el límite de una función definida a trozos en uno de los puntos
frontera debemos recurrir a la definición de los límites laterales y comprobar que existen y
coinciden.
3. PROPIEDADES DE LAS FUNCIONES CONVERGENTES
Unicidad de límite.
Si una función es convergente o tiene límite en un punto, este es único.
Acotación.
Una función que tiene límite en un punto está acotada en un entorno de ese punto.
Operaciones con las funciones convergentes.

3. Si f y g son dos funciones convergentes en a :
lim f ( x) L
g( x) M
x a
=
®
lim
x a
=
®
se verifican las siguientes propiedades:
- ( f ± g)( x) = L ±
M
x a
æ
x L
f
÷ lim - ÷ø
lim ( ) = ; ¹ 0 ®
ö
ç çè
®
si M
M
g
x a
lim - lim[ ( )] ( ) = ; > 0
- ( )( ) = " ÎÂ
®
a f x a L a
x a
®
f x g x LM L
x a
- lim ( f · g)( x) = L ·
M
x ®
a
4. LÍMITES INFINITOS CUANDO X TIENDE A UN NÚMERO REAL
En muchas funciones, cuando x tiende a algunos puntos por la izquierda o por la derecha,
el valor de f (x) no se aproxima a ningún número real si no que se hace cada vez más grande o
cada vez más pequeño. En estos casos decimos que el límite correspondiente es + ¥ o - ¥ ,
respectivamente.
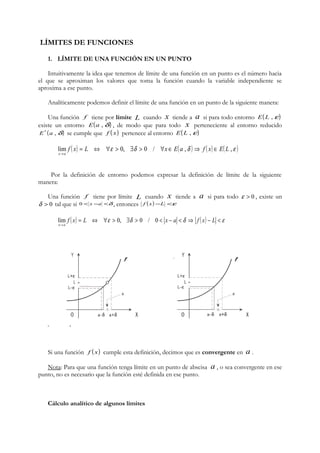
Una función f tiene por límite + ¥ cuando x tiende a a por la izquierda si para todo
número real K , existe d > 0 , tal que si a -d < x < a se verifica que f ( x) > K . Se escribe
f ( x
) = +¥ ® -
lim .
x a
Análogamente para lim
f ( x
) = +¥ ® +
x a
Una función f tiene por límite + ¥ cuando x tiende a a si para todo número real K ,
existe d > 0 , tal que si 0 < x -a <d se verifica que f ( x) > K . Se escribe ( ) = +¥
lim .
®
f x
x a
De forma similar se pueden definir ( ) = -¥ ® -
lim f x
, ( ) = -¥ ® +
x a
lim f x
y f ( x)
x a
lim
x®a
Cuando existe alguno de los seis límites mencionados decimos que la función f tiene una
asíntota vertical en x = a .
5. LÍMITES EN EL INFINITO
5.1 LÍMITES FINITOS EN EL INFINITO
Una función f tiene por límite un número real L cuando x tiende a + ¥ si para
todo e > 0 , existe un número real K , de modo que para cualquier valor de x mayor que K se
verifica que f (x)-L <e . Se escribe lim
f ( x) L
x
=
®+¥

4. Una función f tiene por límite un número real L cuando x tiende a - ¥ si para
todo e > 0 , existe un número real M , de modo que para cualquier valor de x menor que M
se verifica que f (x)-L <e . Se escribe lim
f ( x) L
x
=
®-¥
Cuando una función f tiene alguno de los límites anteriores, decimos que la función
tiene una asíntota horizontal de ecuación y =L .
5.2 LÍMITES INFINITOS EN EL INFINITO
Una función f tiende a + ¥ cuando x tiende a + ¥ si para todo número real K existe
un número real M, de modo que para cualquier x mayor que M se verifica que f (x) es mayor
que K. Simbólicamente:
f ( x) K M x M f ( x) K
lim , /
x
= +¥ Û " ÎÂ $ ÎÂ " > Þ >
®+¥
Análogamente se definen ( ) = -¥
lim , ( ) = +¥
®+¥
f x
x
lim y ( ) = -¥
®-¥
f x
x
lim
®-¥
f x
x
6. CÁLCULO DE LÍMITES
6.1. CÁLCULO DE LÍMITES EN LAS FUNCIONES ELEMENTALES.
Funciones polinómicas
Las funciones polinómicas son convergentes cuando x tiende a a , siendo a un
número real, y su límite coincide con el valor numérico del polinomio en a :
P( x) P(a)
lim
x a
=
®
Las funciones polinómicas, cuando x tiende a ±¥ , se comportan del mismo modo
que su término de mayor grado, siendo su límite ±¥ .
( ) n
P x a x
lim = lim
x ®±¥ x ®±¥
n
Funciones racionales
Las funciones racionales son convergentes cuando x tiende a a , para todo valor de a
perteneciente al dominio de la función:
( )
( )
( )
( ) a Dom f
P a
Q a
P x
Q x
lim
x a
= " Î
®
Para los valores de a que no pertenecen al dominio de la función y que se corresponden
con las raíces del denominador aparecen las indeterminaciones de tipo
K y
0
0 que se
0

5. resuelven estudiando los límites laterales y simplificando los factores comunes del numerador y
denominador, respectivamente.
Al calcular los límites en el infinito de este tipo de funciones aparece la indeterminación
¥ que se resuelve dividiendo numerador y denominador por la máxima potencia o utilizando
¥
la siguiente expresión:
( )
a x
( ) m
m
n
n
P x
lim = lim
Q x
x ®±¥ x ®±¥
b x
El resultado depende de los grados de los polinomios numerador y denominador y denominador,
de forma que:
- Si n > m, el límite es infinito.
n = m, a
- Si el límite es
n
b
m
.
- Si n < m, el límite es cero.
Otras funciones elementales
Para calcular límites en las funciones irracionales, exponenciales y logarítmicas hay que
tener muy presente el dominio de definición de estas funciones
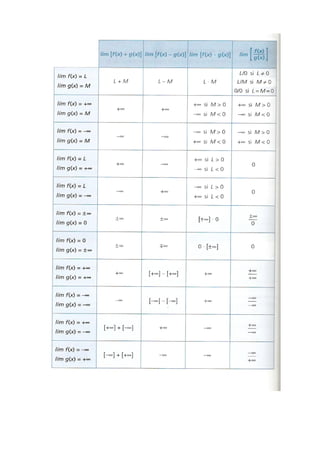
6.2. OPERACIONES CON LÍMITES DE FUNCIONES
Conociendo como se calculan los límites de las funciones elementales y aplicando las
operaciones con límites de funciones podemos calcular todos los demás. La siguiente tabla
muestra todos los casos posibles de cálculo de límites funcionales, cuando la variable x tiende a
un número real, + ¥ o - ¥ . Los recuadros sombreados corresponden a los casos en los cuales
no es posible hallar directamente el límite. Por esta razón, se llaman indeterminaciones y hay
que resolverlas de manera particular.
Para interpretar la tabla debes recordar las propiedades vistas en el apartado 3 del tema
sobre operaciones con límites:
lim[ f ( x) + g( x)] = lim f ( x) + limg( x)
lim[ f ( x) - g( x)] = lim f ( x) -limg( x)
lim[ f ( x) · g( x)] = lim f ( x) · limg( x)
( )
( )
f ( x
)
g( x)
úû ù
lim f x
= lim g x
lim
é
êë

7. Funciones potencial- exponenciales
Los límites de este tipo de funciones se resuelven aplicando la propiedad:
lim[ f ( x) g ( x ) ] = [lim f ( x)]lim g ( x )
Los posibles resultados se recogen en la siguiente tabla:
Las expresiones 00 , ¥0 y 1±¥son indeterminaciones. En este tema sólo aprenderemos
a resolver la última de ellas pues las demás se resuelven utilizando la regla de L’ Hôpital.
Límite de la composición de funciones
Sea la función compuesta g  f , donde g es una función potencial (de exponente
entero o fraccionario), logarítmica o trigonométrica (seno, coseno y tangente) y lim f ( x) = L .
Entonces:
lim( g  f )( x) = limg( f ( x)) = g(lim f ( x)) = g(L)
6.3. RESOLUCIÓN DE INDETERMINACIONES
Todas las indeterminaciones vistas en el apartado anterior se pueden agrupar en los
siguientes tipos:
Indeterminaciones del tipo ¥
¥
Aparecen al calcular límites de cocientes de funciones polinómicas. Su resolución se ha
explicado en el apartado de las funciones racionales.

8. 0
Indeterminaciones del tipo 0
Las indeterminaciones de cocientes de funciones polinómicas se resuelven factorizando
los polinomios numerador y denominador mediante la regla de Ruffini.
Las indeterminaciones de cocientes de funciones irracionales se resuelven multiplicando
numerador y denominador por la expresión conjugada de la función que lleve raíz.
K
Indeterminaciones del tipo 0
Estas indeterminaciones se resuelven estudiando los límites laterales de los cocientes de
funciones que los generan.
Indeterminaciones del tipo 0 ·¥
Estas indeterminaciones se resuelven transformándolas en las del tipo ¥
¥, o en las des
del tipo
0 .
0
Indeterminaciones del tipo ¥ - ¥
Las indeterminaciones con funciones racionales se resuelven operando
convenientemente.
Las indeterminaciones con funciones irracionales se resuelven multiplicando el
numerador y el denominador por la expresión conjugada de la función que lleve raíz.
Indeterminaciones del tipo 1¥
Este tipo de indeterminaciones se resuelven aplicando la siguiente propiedad, que es
válida para 0 x real, + ¥ o - ¥ .
( )
= [ ( )] g ( x ) lim g ( x ) ·[ f ( x
) 1]
( ) lim 1 -
0
ü
= ± ¥
x ® x 0 Þ lim
f x = ex ®
x
lim
g x
0
0
®
®
ïþ
ïý
x x
x x
f x
6.4. CÁLCULO DE LÍMITES UTILIZANDO INFINITÉSIMOS
EQUIVALENTES
Llamamos infinitésimos a las funciones f (x) que tienden a cero cuando x tiende a un
número real, + ¥ o - ¥
f (x) es un infinitésimo Û lim f ( x) = 0

9. Dos infinitésimos son equivalentes si el límite de su cociente es 1.
( ) ( ) ( )
f x g x en x f x
0 » Û =
lim ( ) 1
® g x
x x
0
Cuando f (x) tiende a cero, los infinitésimos equivalentes más importantes son:
sen( f ( x)) » f ( x) tg( f ( x)) » f ( x) ( ( )) [ ( )]
f x 2 - f x »
2
1 cos
ln(1+ f ( x)) » f ( x) a f ( x) -1 » f ( x) ln a
En el cálculo de límites podemos sustituir un infinitésimo por su equivalente siempre que
aparezca multiplicando o dividiendo.
7. ASÍNTOTAS Y RAMAS INFINITAS DE UNA FUNCIÓN
7.1 ASÍNTOTAS VERTICALES
Si alguno de los límites de una función en un punto es infinito, decimos que la función
tiene ramas infinitas verticales. Estas ramas se aproximan a una recta vertical que se llama
asíntota vertical.
La recta x = a es una asíntota vertical de la función f cuando existe al menos uno
de los seis límites siguientes:
lim f ( x
) = +¥ ( ) = +¥ ® -
® +
x a
lim f x
( ) = +¥
x a
lim
®
f x
x a
lim f ( x
) = -¥ ( ) = -¥ ® -
® +
x a
lim f x
( ) = -¥
x a
lim
®
f x
x a
7.2 ASÍNTOTAS HORIZONTALES
Si alguno de los límites en el infinito de una función es un número real, decimos que la
función tiene ramas infinitas horizontales. Estas ramas se aproximan a una recta horizontal
que se llama asíntota horizontal.
La recta y =L es una asíntota horizontal de la función f cuando existe al menos
uno de los siguientes límites:
lim f ( x) L
f ( x) L
x
=
®+¥
lim
x
=
®-¥
7.3 ASÍNTOTAS OBLICUAS
Si una función se aproxima infinitamente a una recta oblicua cuando la variable
independiente tiende a infinito, decimos que la función tiene ramas infinitas oblicuas
hiperbólicas. Estas ramas se aproximan a una recta que se llama asíntota oblicua.

10. La recta y = mx + n es una asíntota oblicua de la función f cuando la pendiente m y la
ordenada en el origen n pueden obtenerse mediante los siguientes límites:
( )
x
= lim n [ f ( x) mx]
m f x
x®±¥
= -
lim
x
®±¥
7.4. RAMAS PARABÓLICAS
Si los valores de una función crecen indefinidamente cuando la variable independiente
tiende a infinito pero sin aproximarse a una recta oblicua, decimos que la función tiene ramas
infinitas oblicuas parabólicas. Las funciones con ramas infinitas parabólicas carecen de
asíntotas oblicuas.
La función f tiene una rama parabólica cuando existe al menos uno de los siguientes
límites y no existen asíntotas oblicuas:
lim ( ) = -¥
( ) = +¥
®-¥
f x
x
lim
®-¥
f x
x
lim ( ) = -¥
( ) = +¥
®+¥
f x
x
lim
®+¥
f x
x