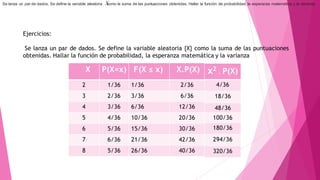
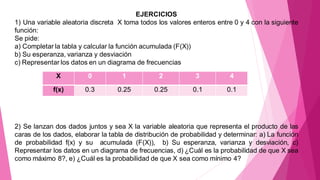
Este documento describe conceptos básicos sobre variables aleatorias, incluyendo su clasificación como discretas o continuas. Explica cómo calcular la probabilidad, esperanza, varianza y desviación estándar para variables aleatorias discretas y continuas. También presenta ejemplos numéricos y gráficos para ilustrar estos conceptos.

1. Prof.: Maria E. Briceño

2. Variable Aleatoria:
Se denomina variable aleatoria (o estocástica) a la función que adjudica eventos posibles
a números reales (cifras), cuyos valores se miden en experimentos de tipo aleatorio.
Estos valores posibles representan los resultados de experimentos que todavía no se
llevaron a cabo o cantidades inciertas.
VariablesAleatoriaDiscreta:
Una variable aleatoria es discreta si los números a los que da lugar
son números enteros. La forma de calcular las probabilidades de una
variable discreta es a través de la función de probabilidad.
VariableAleatoria Continua:
Una variable es continua en caso de que los números a los que dé lugar no sean números
enteros. Es decir, tengan decimales. La probabilidad de que se dé un suceso determinado
correspondiente a una variable aleatoria continua viene establecida por la función de
densidad.

4. -Función de distribución de probabilidad:
La distribución de probabilidad es un modelo teórico que describe la forma en que
varían los resultados de un experimento aleatorio, es decir, nos da todas las
probabilidades de todos los posibles resultados que podrían obtenerse cuando se realiza
un experimento aleatorio. Se clasifican como discretas o continuas.
En la distribución de probabilidad discreta está permitido tomar solo un número
limitado de valores. En la continua, llamada función de densidad y función de
distribución.
La función de distribución describe el comportamiento probabilístico de una variable
aleatoria x asociada a un experimento aleatorio y se representa como: f(x) y es la
Probabilidad de que X tome un valor x, es decir, P(X=x)

5. Función aculada F(x)
La función de distribución acumulada asociada a una variable aleatoria real: X (mayúscula) sujeta a
cierta ley de distribución de probabilidad, es una función matemática de la variable real: x(minúscula);
que describe la probabilidad de que X tenga un valor menor o igual que x. Intuitivamente, asumiendo la
función f como la ley de distribución de probabilidad, la FDA sería la probabilidad de que la variable
aleatoria “ X ” , tome valores menores o iguales a “x”, es decir, P(X ≤ x )

6. Representación grafica de la distribución de probabilidad : para variable aleatoria discreta
y variable aleatoria continua
f(X=x) = P(X=x)
F(X ≤ x) = P(X ≤ x)
f(X)

7. Valor Esperado, Varianza y Desviación de una Variable
Aleatoria Discreta:
• Valor Esperado: La media «µ» o valor esperado «E(X)» es un promedio ponderado
de los valores que asume la variable aleatoria cuando los pesos son las
probabilidades. Es una medida de tendencia central. Cuando se trabaja con una
variable aleatoria discreta, la media o valor esperado se calcula mediante
la siguiente formula:
‚ P(X=x)= f(X=x)
La media µ de una variable aleatoria discreta X se encuentra al multiplicar cada posible
valor de X por su propia probabilidad y luego sumar todos los productos.

8. Varianza: La varianza, o V(X), es un promedio ponderado de las desviaciones al cuadrado
de una variable aleatoria de su media. La varianza o V(X) se
calcula con la siguiente formula:
Se debe recordar que la varianza es una medida de variabilidad o dispersión y se mide en las
mismas unidades que en variable aleatoria original.

9. • :Desviación estándar
La desviación estándar σ es la raíz cuadrada positiva de la varianza y mide en cuanto se
aleja o se acerca los valores de la variable al valor promedio calculado « µ » .
σ = √

10. Ejercicios:
Se lanza un par de dados. Se define la variable aleatoria {X} como la suma de las puntuaciones
obtenidas. Hallar la función de probabilidad, la esperanza matemática y la varianza
Se lanza un par de dados. Se define la variable aleatoria como la suma de las puntuaciones obtenidas. Hallar la función de probabilidad, la esperanza matemática y la varianza
X P(X=x) F(X ≤ x) X.P(X)
2 1/36 1/36 2/36
3 2/36 3/36 6/36
4 3/36 6/36 12/36
5 4/36 10/36 20/36
6 5/36 15/36 30/36
7 6/36 21/36 42/36
8 5/36 26/36 40/36
x2 . P(X)
4/36
18/36
48/36
100/36
180/36
294/36
320/36

11. X P(X=x) F(X ≤ x) X.P(X) x2 . P(X)
9 4/36 30/36 36/36 324/36
10 3/36 33/36 30/36 300/36
11 2/36 35/36 22/36 242/36
12 1/36 36/36 12/36 144/36
∑252/36 ∑54.83
µ = 7
= 54.83‐‐(7̂ ^ 2)
=5.83
=√5.83
= 2.415
µ=E(x)
Continuación

12. P(X ≤ 6 ) = 15/36
P(X ≥ 10) = 6/36
P( 9 < X ≤ 12) =6/36

13. 2) Sea X una variable aleatoria discreta cuya función de probabilidad es::
X P(X=x) F( X ≤ x) X.P(X) x2 . P(X)
0 0.1 0-1 0 0
1 0.2 0.3 0.2 0.2
2 0.1 0.4 0.2 0.4
3 0.4 0.8 3.6
445 0.1 1
2.5
4
5
0.1
0.1
0.9
1.0
1.6
2.5 8.3
2.5
= 8.3 –(2.5 )^2
=2.05
= 1.432

14. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 1 2 3 4 5 6
f(x)
probabilidad
Variable X (discreta)
DIAGRAMA DE FRECUENCIA

15. 3)Se lanza 3 monedas juntas, sea X la variable aleatoria que indica el numero de caras obtenidas .
Hallar :
a) Función de probabilidad y su acumulada
b) La esperanza, varianza y desviación
c) P(X sea como mínimo 2 ),
d) P(X sea como maximo1)
Solución : C
C
S
=

16. X P(X=x) F( X ≤ x) X.P(X) x2 .P(X)
0 1/8 1/8 0 0
1 3/8 4/8 3/8 3/8
2
3
3/8
1/8
7/8
8/8
6/8
3/8
12/8
9/8
= 1
=12/8 =24/8
1.5
= 3 −(1.5)
= √ 0.75
= 0.866
c) P(X sea como mínimo 2 )=P(X≥2)= 4/8=0.5
d) P(X sea como maximo1) = P(X≤1)= F( 1) = 0.5
a)
b)

17. X 0 1 2 3 4
f(x) 0.3 0.25 0.25 0.1 0.1
EJERCICIOS
1) Una variable aleatoria discreta X toma todos los valores enteros entre 0 y 4 con la siguiente
función:
Se pide:
a) Completar la tabla y calcular la función acumulada (F(X))
b) Su esperanza, varianza y desviación
c) Representar los datos en un diagrama de frecuencias
2) Se lanzan dos dados juntos y sea X la variable aleatoria que representa el producto de las
caras de los dados, elaborar la tabla de distribución de probabilidad y determinar: a) La función
de probabilidad f(x) y su acumulada (F(X)), b) Su esperanza, varianza y desviación, c)
Representar los datos en un diagrama de frecuencias, d) ¿Cuál es la probabilidad de que X sea
como máximo 8?, e) ¿Cuál es la probabilidad de que X sea como mínimo 4?

18. 3) En una región se cobra a los visitantes de los parques naturales, estimando que la variable
aleatoria número de personas que visitan el parque en coche sigue la siguiente distribución:
X 1 2 3 4 5
P(X =x ) 0,15 0,2 0,35 0,2 0,1
a) Hallar el número medio de visitantes por vehículos
b) Hallar cuánto debe pagar cada visitante para que la ganancia por coche sea 2 euros
c) Representar los datos en un diagrama de frecuencia aculada
d) Determinar P(X≥2).
4) Se lanza un par de dados. Se define la variable aleatoria {X} como el producto de las
puntuaciones obtenidas. Hallar (de acuerdo al espacio muestral),a)La función de
probabilidad, b) La esperanza matemática y c)La varianza

19. 5)En un recipiente hay 5 marcadores rojos, 4 marcadores verdes y 3 marcadores negros . Si se
selecciona al azar dos marcadores (sin reemplazo) y la variable aleatoria X es el numero de
marcadores rojos extraídos, determine :
a) Función de probabilidad y su acumulada
b) La esperanza, varianza y desviación
c) P(X sea como mínimo 2 ),
d) P(X sea como maximo1)
e)Que como mínimo hayan 2 marcadores rojos en los seleccionados