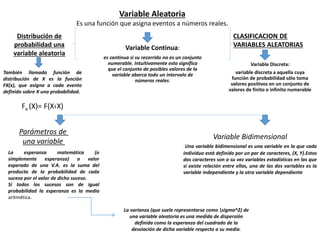
Una variable aleatoria es una función que asigna eventos a números reales. Existen tres tipos de variables aleatorias: continuas, discretas y bidimensionales. La distribución de probabilidad de una variable aleatoria asigna una probabilidad a cada posible valor. Los parámetros clave de una variable aleatoria son la esperanza matemática y la varianza.

1. Variable Aleatoria
Es una función que asigna eventos a números reales.
Distribución de
probabilidad una
variable aleatoria
También llamada función de
distribución de X es la función
FX(x), que asigna a cada evento
definido sobre X una probabilidad.
Fx (X)= F(X‹X)
CLASIFICACION DE
VARIABLES ALEATORIASVariable Continua:
es continua si su recorrido no es un conjunto
numerable. Intuitivamente esto significa
que el conjunto de posibles valores de la
variable abarca todo un intervalo de
números reales.
Variable Discreta:
variable discreta a aquella cuya
función de probabilidad sólo toma
valores positivos en un conjunto de
valores de finito o infinito numerable
Variable Bidimensional
Una variable bidimensional es una variable en la que cada
individuo está definido por un par de caracteres, (X, Y).Estos
dos caracteres son a su vez variables estadísticas en las que
sí existe relación entre ellas, una de las dos variables es la
variable independiente y la otra variable dependiente
Parámetros de
una variable
La esperanza matemática (o
simplemente esperanza) o valor
esperado de una V.A. es la suma del
producto de la probabilidad de cada
suceso por el valor de dicho suceso.
Si todos los sucesos son de igual
probabilidad la esperanza es la media
aritmética.
La varianza (que suele representarse como sigma^2) de
una variable aleatoria es una medida de dispersión
definida como la esperanza del cuadrado de la
desviación de dicha variable respecto a su media.

2. Supóngase que la producción de un día de 850 piezas manufacturadas contiene 50
piezas que no cumplen con los requerimientos del cliente. Se seleccionan del lote dos piezas
al azar y sin reemplazo. Sea la variable aleatoria X igual al número de piezas de la
muestra que no cumplen. ¿Cuál es la función de distribución acumulada de X?
SOLUCIÓN:
La pregunta puede contestarse encontrando primero la función de masa de
probabilidad de X.
P(x=0)= (800/850)(799/849)=0,886
P(x=1)=2(800/850)(50/849)=0,111
P(x=2)=(50/850)(49/849)=0,003
Por lo tanto,
F(0)=P(x≤ 0 )=0.886
F(1)=P(x ≤ 1)=0.886+0,111=0,997
F(2)=P(x ≤ 2)=1
EJERCICIO