aprobechalo valora el sacrificio del auto de ete libro

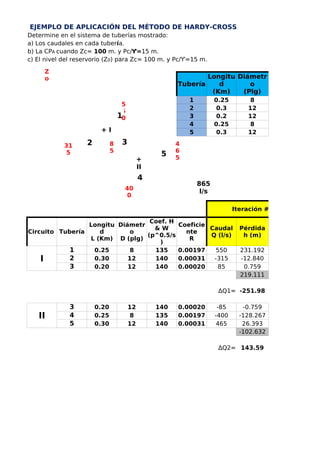
1. EJEMPLO DE APLICACIÓN DEL MÉTODO DE HARDY-CROSS
Determine en el sistema de tuberías mostrado:
Tubería
1 0.25 8
2 0.3 12
3 0.2 12
4 0.25 8
5 0.3 12
Iteración #1
Circuito Tubería
I
1 0.25 8 135 0.00197 550 231.192
2 0.30 12 140 0.00031 -315 -12.840
3 0.20 12 140 0.00020 85 0.759
219.111
ΔQ1= -251.98
II
3 0.20 12 140 0.00020 -85 -0.759
4 0.25 8 135 0.00197 -400 -128.267
5 0.30 12 140 0.00031 465 26.393
-102.632
ΔQ2= 143.59
a) Los caudales en cada tubería.
b) La CPA cuando Zc= 100 m. y Pc/Ƴ=15 m.
c) El nivel del reservorio (Z0) para Zc= 100 m. y Pc/Ƴ=15 m.
Longitu
d
(Km)
Diámetr
o
(Plg)
Longitu
d
L (Km)
Diámetr
o
D (plg)
Coef. H
& W
(p^0.5/s
)
Coeficie
nte
R
Caudal
Q (l/s)
Pérdida
h (m)
Zo
550
1
+ I
31 2 3
5
85
465
5 +
II4
40
0
865
l/s

2. 135
140
140
135
140
Iteración #1 Iteración #2 Iteración #3 Iteración #4
h/Q h/Q h/Q
0.420 298.02 74.416 0.250 254.01 55.370 0.218 253.10
0.041 -566.98 -38.089 0.067 -610.99 -43.739 0.072 -611.90
0.009 -310.57 -8.339 0.027 -362.37 -11.093 0.031 -359.30
0.470 27.989 0.344 0.538 0.320
ΔQ1= -44.01 ΔQ1= -0.91 ΔQ1=
0.009 310.57 8.339 0.027 362.37 11.093 0.031 359.30
0.321 -256.41 -56.341 0.220 -248.62 -53.216 0.214 -252.60
0.057 608.59 43.421 0.071 616.38 44.455 0.072 612.40
0.386 -4.581 0.318 2.332 0.317
ΔQ2= 7.79 ΔQ2= -3.98 ΔQ2=
C
(p^0.5/
s)
Caudal
Q (l/s)
Pérdida
h (m)
Caudal
Q (l/s)
Pérdida
h (m)
Caudal
Q (l/s)

3. Iteración #4 Iteración #5 Iteración #6
Caudal
Q (l/s)
Pérdida
h (m)
Caudal
Q (l/s)
Pérdida
h (m)
h/Q h/Q h/Q
Pérdida
h (m)
55.004 0.217 252.72 54.851 0.217 252.71 54.848 0.217
-43.859 0.072 -612.28 -43.910 0.072 -612.29 -43.911 0.072
-10.920 0.030 -359.61 -10.937 0.030 -359.58 -10.935 0.030
0.225 0.319 0.004 0.319 0.002 0.319
-0.38 ΔQ1= -0.01 ΔQ1= 0.00
10.920 0.030 359.61 10.937 0.030 359.58 10.935 0.030
-54.802 0.217 -252.67 -54.831 0.217 -252.71 -54.846 0.217
43.926 0.072 612.33 43.916 0.072 612.29 43.911 0.072
0.043 0.319 0.021 0.319 0.000 0.319
-0.07 ΔQ2= -0.04 ΔQ2= 0.00

4. PROBLEMA 4: En la Fig. 3 El sistema de tuberías se encuentra de Hardy-Cross (u otro alternativo) determinar los caudales y 85
l/s 194
l/s
Tubería Longitud (Km)Diámetro (Plg) C (Pie^0.5/s)
1 0.52 8 140
2 0.62 6 140
3 0.51 6 140
4 0.63 8 140
5 0.70 6 140
6 1.60 6 140
7 0.72 8 140
Utilizando el Método de Hardy-Cross
52
Coeficiente: R = (1.72*10^6*L)/(C^1.85*D^4.87)
Factor de aceleración de convergencia: n=1.85
Circuito Tubería
I
Longitud
L (Km)
Diámetro
D (Plg)
Coef. de H &
W
C
(pies^0.5/s)
1 0.52 8 140
2 0.62 6 140
3 0.51 6 140
44
1 7
33
2 + I 4 + I
I
65
3 5
81
26 48

5. I
4 0.63 8 140
II
4 0.63 8 140
5 0.70 6 140
6 1.60 6 140
7 0.72 8 140
Luego de 6 iteraciones, obtenemos un error de pérdida
con lo cual concluye el proceso iterativo.
Obteniendo los siguientes caudales y pérdidas finales
Circuito Tubería
I
1234
II
4567

6. tuberías se encuentra en un plano horizontal. Empleando el método
determinar los caudales y pérdidas de carga en el sistema.
2
44 20
7
+ I
I
6 24
5
15
9
Iteración #1 Iteración #2 Iteración #Coeficient
Caudal
Q (l/s)
Pérdida
h (m)
h/Q h/Q
eR
Caudal
Q (l/s)
Pérdida
h (m)
Caudal
Q (l/s)
0.00383 -85 -14.209 0.167 ### ### 0.170 ###
0.01853 -33 -11.946 0.362 ### ### 0.380 ###
0.01525 48 19.654 0.409 ### ### 0.395 ###

7. 0.00464 65 10.480 0.161 ### ### 0.171 ###
3.979 1.100 1.956 1.117
ΔQ1= -1.956 ΔQ1= -0.947 ΔQ1=
0.00464 -65 -10.480 0.161 ### ### 0.171 ###
0.02093 9 1.219 0.135 2.531 0.117 0.046 1.205
0.04783 24 17.104 0.713 ### 9.567 0.546 ###
0.00530 44 5.819 0.132 ### 4.336 0.116 ###
13.662 1.142 2.153 0.878
ΔQ2= -6.469 ΔQ2= -1.326 ΔQ2=
error de pérdida ΔQ < 0.001
pérdidas finales:
Resultados
CaudFainlales
Q (l/s)
Pérdida
h (m)
-88.147 ###
-36.147 ###
44.853 ###
69.945 ###
0.003
ΔQ1= -0.001
-69.945 ###
0.907 0.017
15.907 7.992
35.907 3.995
0.002
ΔQ2= -0.001

8. h/Q h/Q h/Q
### 0.172 ### ### 0.172 ### ### 0.172
### 0.389 ### ### 0.391 ### ### 0.391
### 0.388 ### ### 0.387 ### ### 0.387
método
Iteración #3 Iteración #4 Iteración #5
Pérdida
h (m)
Caudal
Q (l/s)
Pérdida
h (m)
Caudal
Q (l/s)
Pérdida
h (m)

9. ### 0.171 ### ### 0.172 ### ### 0.172
0.416 1.121 0.078 1.122 0.014 1.122
-0.201 ΔQ1= -0.038 ΔQ1= -0.007
### 0.171 ### ### 0.172 ### ### 0.172
0.030 0.025 0.960 0.019 0.020 0.915 0.018 0.019
8.272 0.510 ### 8.041 0.504 ### 8.000 0.503
4.057 0.112 ### 4.006 0.111 ### 3.997 0.111
0.372 0.818 0.066 0.807 0.012 0.805
-0.246 ΔQ2= -0.044 ΔQ2= -0.008

10. Iteración #6
h/Q
Caudal
Q (l/s)
Pérdida
h (m)
### ### 0.172
### ### 0.391
### ### 0.387

11. ### ### 0.172
0.003 1.122
ΔQ1= -0.001
### ### 0.172
0.907 0.017 0.019
### 7.992 0.502
### 3.995 0.111
0.002 0.805
ΔQ2= -0.001

12. EJEMPLO DE APLICACIÓN DEL MÉTODO DE HARDY-CROSS
Caso de seudo-circuito / seudo-tubería
En el sistema de los 3 reservorios, determine los caudales que transportan las tuberías, cota piezométrica en el punto D
Circuito Tubería
1
1 4 10 120 0.01 -40
2 6 8 120 0.06 20
4
Iteración #1
ΔQ1=
2
2 6 8 120 ### -20.000
3 5 6 120 ### -57.500
5
ΔQ2=
Longitu
d
L (Km)
Diámet
ro
D (Plg)
Coef. de H &
W
C (pies^0.5/s)
Coeficient
eR
Caudal
Q (l/s)
100
m
91 m 4
+
1 1
2
40 20 5
+
2.5 2
l/s 3
57.
5

13. que transportan las tuberías, y la
Tubería Longitud (KmD)iámetro (PlgC) (Pie^0.5/s)
1 4 10 120
2 6 8 120
3 5 6 120
ΔQ1= -[Ʃh+(ZA-ZB)]/[1.85*Ʃ(h/Q)]
ΔQ2= -[Ʃh+(ZB-ZC)]/[1.85*Ʃ(h/Q)]
80
m
Iteración #1 Iteración #2 Iteración #3
Pérdida
Caudal
Q (l/s)
Pérdida
h (m)
h/Q h/Q
h (m)
Caudal
Q (l/s)
Pérdida
h (m)
-12.159 0.304 -46.072 -15.793 0.343 ### ###
14.999 0.750 -14.121 -7.878 0.558 ### ###
9.000 9.000 9.000
11.839 1.054 -14.671 0.901 ###
-6.072 ΔQ1= 8.805 ΔQ1= 7.156
-14.999 0.750 14.121 7.878 0.558 ### ###
### 6.225 -29.451 ### 3.525 ### ###
11.000 11.000 ###
### 6.975 -84.934 4.083 ###
28.049 ΔQ2= 11.245 ΔQ2= 3.819

14. Iteración #3 Iteración #4 Iteración #5 Iteración #6
Caudal
Q (l/s)
Pérdida
h (m)
Caudal
Q (l/s)
Pérdida
h (m)
Caudal
Q (l/s)
h/Q h/Q h/Q
0.286 ### ### 0.239 ### ### 0.214 ###
0.639 ### ### 0.528 ### ### 0.476 ###
9.000 9.000
0.925 ### 0.766 ### 0.690
ΔQ1= 3.644 ΔQ1= 1.748 ΔQ1=
0.639 ### 6.977 0.528 ### 5.566 0.476 ###
2.342 ### ### 1.917 ### ### 1.674 ###
### ###
2.981 ### 2.445 ### 2.149
ΔQ2= 2.124 ΔQ2= 0.996 ΔQ2=

15. Iteración #6 Iteración #7 Iteración #8
Pérdida
Caudal
Q (l/s)
Pérdida
h (m)
Caudal
Q (l/s)
Pérdida
h (m)
h/Q h/Q h/Q
h (m)
### 0.202 ### ### 0.197 ### ### 0.194
### 0.449 ### ### 0.438 ### ### 0.434
9.000 9.000 9.000
### 0.651 ### 0.635 ### 0.628
0.758 ΔQ1= 0.316 ΔQ1= 0.127
4.923 0.449 ### 4.660 0.438 ### 4.550 0.434
### 1.558 ### ### 1.506 ### ### 1.485
### ### ###
### 2.007 ### 1.944 ### 1.918
0.438 ΔQ2= 0.180 ΔQ2= 0.073

16. Iteración #9
h/Q
Caudal
Q (l/s)
Pérdida
h (m)
### ### 0.194
### ### 0.432
9.000
### 0.625
ΔQ1= 0.051
### 4.507 0.432
### ### 1.476
###
### 1.908
ΔQ2= 0.029

17. PROBLEMA 3: ¿Cuáles son los gastos que fluyen por las tuberías El nivel de agua en A se encuentra en la cota 91.40
SOLUCIÓN:
Utilizando el Método de Hardy-Cross
Coeficiente: R = (1.72*10^6*L)/(C^1.85*D^4.87)
Factor de aceleración de convergencia: n=1.85
91.40
m.
5 10
51.20
m. 4
Circuito Tubería
1
0 +
3
Longitu
d
L (Km)
+
1 1 20 2
Diámet
ro
D (Plg)
6
60
Coef. de H &
W
C (pies^0.5/s)
+
2
60
Coeficiente
R
1 (*) 1.22 16 100 0.000573
2(**) 0.61 8 140 0.004492
6
2
2(**) 0.61 8 140 0.004492

18. 2 3 1.5 10 130 0.004274
7
3
1(*) 1.22 16 100 0.000573
4 6.1 12 90 0.014122
5
Luego de 7 iteraciones, obtenemos un error de pérdida
con lo cual concluye el proceso iterativo.
Obteniendo los siguientes caudales finales:
Resultados
FCianuadleasl
Q (l/s)
Circuito Tubería
1 1 (*) -150.308
2(**) 0.453
6
2 2(**) -0.453
3 -83.365
7
3 1(*) 150.308
4 67.396
5

19. fluyen por las tuberías del sistema mostrado en la Fig. 2?
91.40 m, B en la 85.30 m, C en la 70 m, y D en la 51.20 m
Tubería
Longitud
(Km)
Diámet
ro
(Plg)
C
(p^0.5/
s)
1 1.22 16 100
2 0.61 8 140
3 1.5 10 130
4 6.1 12 90
85.30 m.
7
70.0
m.
Iteración #1 Iteración #2 Iteración #3
Caudal
Q (l/s)
Pérdida
h (m)
h/Q h/Q
3
60
Caudal
Q (l/s)
Pérdida
h (m)
Caudal
Q (l/s)
-100 -2.870 0.029 ### -5.235 0.038 ###
20 1.147 0.057 8.563 0.239 0.028 5.359
6.1 6.1
4.377 0.086 1.104 0.066
ΔQ1= -27.503 ΔQ1= -9.079 ΔQ1=
-20 -1.147 0.057 -8.563 -0.239 0.028 -5.359

20. -60 -8.325 0.139 ### -12.913 0.170 ###
15.300 15.300
5.828 0.196 2.148 0.198
ΔQ2= -16.066 ΔQ2= -5.875 ΔQ2=
100 2.870 0.029 ### 5.235 0.038 ###
60 27.509 0.458 ### 37.459 0.528 ###
-40.200 -40.200
-9.821 0.487 2.494 0.566
ΔQ3= 10.897 ΔQ3= -2.381 ΔQ3=
de pérdida ΔQ < 0.001

21. Iteración #3 Iteración #4 Iteración #5
Pérdida
Caudal
Q (l/s)
Pérdida
h (m)
Caudal
Q (l/s)
Pérdida
h (m)
h/Q h/Q h/Q
h (m)
-5.713 0.039 ### -5.998 0.040 ### -6.071 0.040
0.100 0.019 1.861 0.014 0.008 0.894 0.004 0.004
6.1 6.1 6.1
0.487 0.058 0.116 0.048 0.032 0.045
### ΔQ1= ### ΔQ1= ###
-0.100 0.019 -1.861 -0.014 0.008 -0.894 -0.004 0.004

22. ### 0.181 ### ### 0.183 ### ### 0.183
### ### ###
0.381 0.200 0.120 0.190 0.015 0.188
### ΔQ2= ### ΔQ2= ###
5.713 0.039 ### 5.998 0.040 ### 6.071 0.040
### 0.513 ### ### 0.509 ### ### 0.507
### ### ###
0.678 0.553 0.336 0.549 0.098 0.547
### ΔQ3= ### ΔQ3= ###

23. Iteración #6 Iteración #7
Caudal
Q (l/s)
Pérdida
h (m)
h/Q h/Q
Caudal
Q (l/s)
Pérdida
h (m)
### -6.093 0.041 ### -6.099 0.041
0.546 0.001 0.003 0.453 0.001 0.002
6.1 6.1
0.008 0.043 0.002 0.043
ΔQ1= ### ΔQ1= ###
-0.546 -0.001 0.003 -0.453 -0.001 0.002

24. ### ### 0.183 ### ### 0.184
### ###
0.003 0.186 0.000 0.186
ΔQ2= ### ΔQ2= ###
### 6.093 0.041 ### 6.099 0.041
### ### 0.506 67.396 ### 0.506
### ###
0.029 0.547 0.008 0.547
ΔQ3= ### ΔQ3= ###