Asintoti
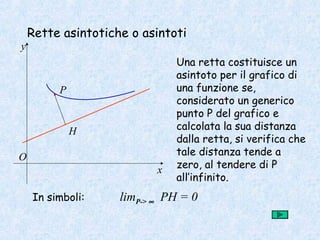
- 1. Rette asintotiche o asintoti Una retta costituisce un asintoto per il grafico di una funzione se, considerato un generico punto P del grafico e calcolata la sua distanza dalla retta, si verifica che tale distanza tende a zero, al tendere di P all’infinito. x y O P H In simboli: limP-> ∞ PH = 0
- 2. Si tratta di esplicitare il calcolo simbolico della definizione. A tale scopo occorre: a) calcolare la distanza punto-retta, e b) di stabilire come far tendere il punto P all’infinito. Si presentano tre casi: 1. La retta asintotica è parallela all’asse x (si parla di asintoto orizzontaleasintoto orizzontale). 2. La retta è parallela all’asse y ( si parla di asintotoasintoto verticale).verticale). 3. La retta è una generica retta del piano: né parallela ad un asse né all’altro ( si parla di asintoto obliquoasintoto obliquo)
- 3. ASINTOTO ORIZZONTALE In questo caso il limite della definizione di asintoto si esplicita nel seguente modo: La distanza PH è espressa da: PH = | f(x) – l | e per far tendere P all’infinito occorre far tendere la sua ascissa x ad infinito. In conclusione: limx-> ∞ | f(x) – l | = 0limx-> ∞ | f(x) – l | = 0 y = l x y O P(x;f(x)) Hf(x) l
- 4. ASINTOTO VERTICALE x y O P(x;f(x)) x = xo xo In questo caso il limite della definizione di asintoto si esplicita nel seguente modo: La distanza PH è espressa da: PH = | x – xO | e per far tendere P all’infinito occorre far tendere la sua ascissa x ad xO. In conclusione: limx-> xo | x – xO | = 0limx-> xo | x – xO | = 0
- 5. ASINTOTO OBLIQUO x y O In questo caso il limite della definizione di asintoto si esplicita nel seguente modo: La distanza PH, dalla retta asintotica y = mx + q è espressa da: | mx – f(x) + q | PH = ———————— √ m2 + 1 il punto P tende all’infinito per x tendente all’infinito: P(x;f(x)) H y = mx +q
- 6. Il limite della definizione diventa: limx-> ∞ | mx – f(x) + q | = 0 ( siccome il risultato deve essere zero, la quantità al denominatore, in quanto costante numerica, può essere trascurata). Va notato che tutte le quantità presenti nella definizione sono note: 1. l’equazione della retta y = mx + q, 2. l’equazione f(x) della funzione, 3. il risultato del limite.
- 7. Fine della trattazione teorica Termina lo svolgimento della teoria relativa agli asintoti di una funzione. Ora si apre il capitolo applicativo della teoria relativo alla ricerca degli eventuali asintoti di una funzione di equazione assegnata.
- 8. PROBLEMA INVERSO Si pone il problema di stabilire sotto quali condizioni una data funzione ammette asintoti. Caso dell’asintoto orizzontaleCaso dell’asintoto orizzontale. Ipotesi: se la funzione y = f(x), è tale che il limite: limx-> ∞ f(x), esiste e vale l, finito, cioè se si verifica che: limx-> ∞ f(x) = l Tesi: allora il grafico della funzione ammette asintoto orizzontale y = l.
- 9. Caso dell’asintoto verticaleCaso dell’asintoto verticale. Ipotesi: se la funzione y = f(x), è tale che il limite: limx-> xo f(x), esiste e vale infinito, cioè se si verifica che: limx-> xo f(x) = ∞ Tesi: allora il grafico della funzione ammette asintoto verticale: x = xo.
- 10. Asintoto obliquo Premessa: Condizione necessaria affinché la funzione f(x) ammetta asintoto obliquo è che risulti: limx-> ∞ f(x) = ∞ N.B.: il limite infinito costituisce solo una condizione necessaria: Se tale limite è verificato NON è detto che la funzione ammetta asintoto obliquo. Comunque se tale limite NON è verificato allora la funzione NON ammette asintoto obliquo.
- 11. Caso dell’asintoto obliquoCaso dell’asintoto obliquo. In questo caso si tratta di calcolare i coefficienti dell’equazione della retta asintotica: y = mx + q. Quindi il problema consiste nel ricercare le incognite del problema: i due coefficienti mm e qq. A questo scopo ricorriamo alla definizione data di asintoto obliquo, espressa dal limite: limx-> ∞ | mx – f(x) + q | = 0. in cui, ora, m e q figurano come parametri incogniti.
- 12. Procedura risolutiva: Se il limite limx-> ∞ | mx – f(x) + q | = 0. risulta nullo, a maggior ragione risulta nullo anche il limite: | mx – f(x) + q | limx-> ∞ ———————— = 0 x Che può essere scritto: mx f(x) q limx-> ∞ | —— - —— + —— | = 0 x x x
- 13. Da cui si ha: f(x) q limx-> ∞ | m - —— + — | = 0 x x il limite q limx-> ∞ — x vale zero, perciò il limite di sopra diventa: f(x) limx-> ∞ | m - —— | = 0 x Da questa relazione si può ricavare il parametro m: f(x) mm = limx-> ∞ —— (*) x
- 14. Una volta determinato m, si passa a calcolare il parametro q. Dal limite della definizione: limx-> ∞ | mx – f(x) + q | = 0. dopo aver sostituito il valore calcolato di mm, si può ricavare q: qq = limx-> ∞ [ f(x) - mmx ] (**) in conclusione la funzione ammette asintoto obliquo se i due limiti (*) e (**) , che permettono di ricavare i due parametri mm e qq, esistonoesistono e sono finitifiniti.
- 15. In conclusione per calcolare un asintoto obliquo si devono calcolare i due limiti: f(x) mm = limx-> ∞ —— xqq = limx-> ∞ [ f(x) - mmx ] Questi due limiti devono esistere ed essere finiti. N.B.: anche se uno dei due risultasse infinito, allora l’asintoto NON esiste.
- 16. Caso particolare relativo alle funzioni razionali fratte. Per le funzioni di equazione: P(x) f(x) = ——— con P(x), Q(x) polinomi, Q(x) esiste asintoto obliquo quando il grado del numeratore supera di una unità quello del denominatore. Si perviene, per via elementare, all’equazione dell’asintoto eseguendo la divisione P(x) : Q(x) . Il quoziente di tale divisione dà l’equazione dell’asintoto.
- 17. Se P(x) è di 1 grado superiore a quello di Q(x), allora il quoziente risulta di 1° grado P(x) Q(x) ——— ………. mx + q ——— quoziente resto L’equazione dell’asintoto è data da: y = mx + q .