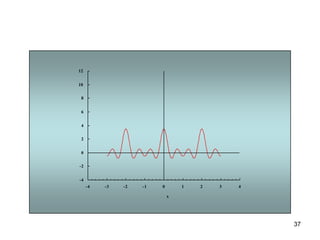
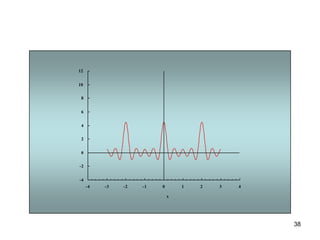
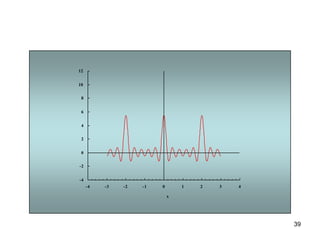
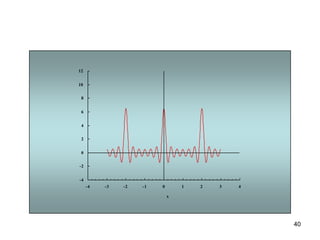
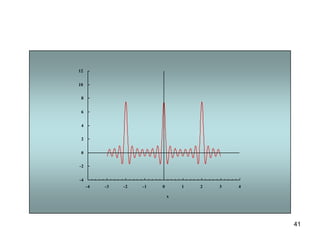
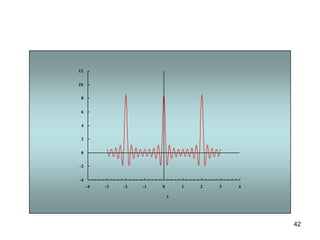
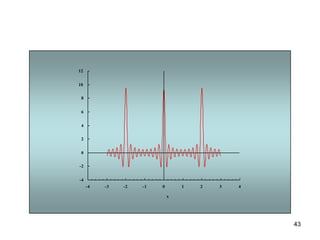
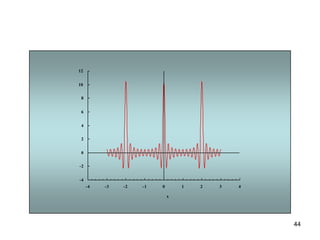
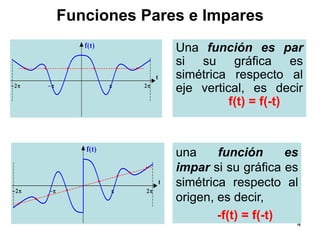
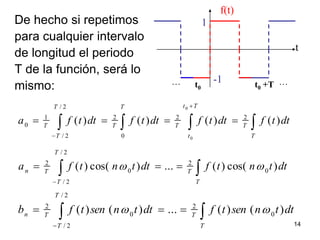
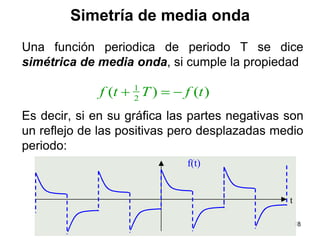
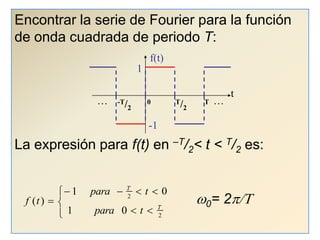
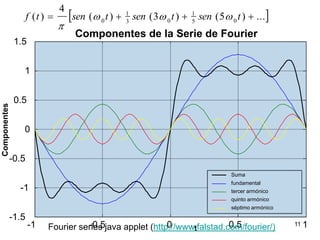
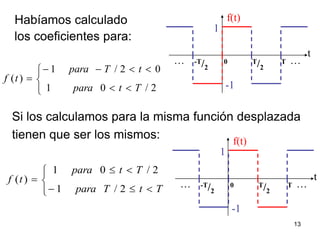
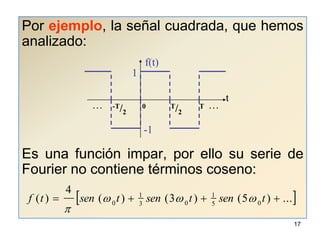
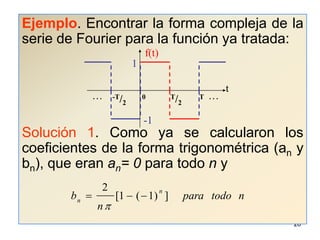
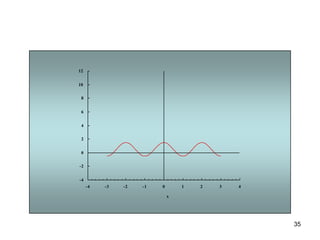
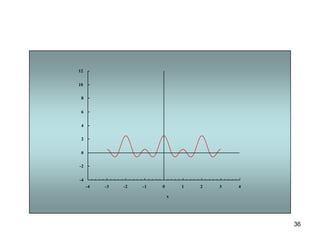
1) El documento describe la serie de Fourier, una representación de funciones periódicas como suma de funciones seno y coseno. 2) Explica conceptos como ortogonalidad, funciones pares e impares y cómo calcular los coeficientes de la serie. 3) Proporciona un ejemplo numérico de la serie de Fourier para una función de onda cuadrada.

1. 1Series de Fourier"Series de Fourier, Transformadas de Fourier y Aplicaciones",Genaro González

2. 2Serie trigonométrica de FourierAlgunas funciones periódicas f(t) de periodo T pueden expresarse por la siguiente serie, llamada serie trigonométrica de Fourierf(t) = ½ a0 + a1cos(w0t) + a2cos(2w0t) + ... + b1sen(w0t) + b2sen(2w0t) + ...Donde w0 = 2p/T se denomina frecuencia fundamental.

3. 3OrtogonalidadSe dice que las funciones del conjunto {fk(t)} son ortogonales en el intervalo a < t < b si dos funciones cualesquiera fm(t), fn(t) de dicho conjunto cumplen:Ejemplo: Demostrar que las funciones sen t y cos t son ortogonales en el intervalo –p < t <p:

4. 4Funciones Pares e ImparesUna función es par si su gráfica es simétrica respecto al eje vertical, es decir f(t) = f(-t)una función es impar si su gráfica es simétrica respecto al origen, es decir, -f(t) = f(-t)

5. 5¿Cómo calcular los coeficientes de la serie?

6. 6f(t)1t. . . -T/2 0T/2 T . . .-1w0= 2p/TEncontrar la serie de Fourier para la función de onda cuadrada de periodo T:La expresión para f(t) en –T/2< t < T/2 es:

7. 7Coeficientea0:

8. 8Coeficientesan:

9. 9Coeficientes bn:

10. 10Finalmente, la serie de Fourier queda como En la siguiente figura se muestran: la componente fundamental y los armónicos 3, 5 y 7, así como la suma parcial de estos primeros cuatro términos de la serie para w0 = p (w0= 2p/T), es decir, T = 2:

11. 11Componentes de la Serie de Fourier1.510.50Componentes-0.5Sumafundamental-1tercer armónicoquinto armónicoséptimo armónico-1.5-1-0.500.51tFourier series java applet (http://www.falstad.com/fourier/)

12. 12Nota:Para expresarse como serie de Fourier f(t), no necesita estar centrada en el origen. Simplemente debemos tomar el intervalo, donde está definida, como el periodo de la serie. La ortogonalidad de las funciones seno y coseno no sólo se da en el intervalo de –T/2 a T/2, sino en cualquier intervalo que cubra un periodo completo: de t0 a t0 + T, con t0 arbitrario, con el mismo resultado.

13. 13f(t)1t. . . -T/2 0T/2 T . . .-1f(t)Habíamos calculado los coeficientes para:1t. . . -T/2 0T/2 T . . .-1Si los calculamos para la misma función desplazadatienen que ser los mismos:

14. 14f(t)De hecho si repetimos para cualquier intervalo de longitud el periodo T de la función, será lo mismo:1t-1. . . t0 t0 +T . . .

15. Actividad 1Calcular la serie de Fourier de la función periódica:

16. 16 Como la función sen(nw0t) es una función impar para todo n y la función cos(nw0t) es una función par para todo n, es de esperar que:Si f(t) es par, su serie de Fourier no contendrá términos seno, por lo tanto bn= 0 para todo n.Si f(t) es impar, su serie de Fourier no contendrá términos coseno, por lo tanto an= 0 para todo n.

17. 17f(t)1t. . . -T/2 0T/2 T . . .-1Por ejemplo, la señal cuadrada, que hemos analizado:Es una función impar, por ello su serie de Fourier no contiene términos coseno:

18. 18f(t) tSimetría de media ondaUna función periodica de periodo T se dice simétrica de media onda, si cumple la propiedadEs decir, si en su gráfica las partes negativas son un reflejo de las positivas pero desplazadas medio periodo:

19. 19Simetrías y Coeficientes de Fourier

20. 20

21. 21

22. 22Actividad 2

23. 23Forma compleja de la serie de FourierConsideremos la serie de Fourier para una función periódica f(t), con periodo T = 2p/w0.Es posible obtener una forma alternativa usando las fórmulas de Euler:

24. 24Sustituyendo:Y usando el hecho de que 1/i = -i:Y definiendo:

25. 25A la expresión obtenidase le llama forma compleja de la serie de Fourier y sus coeficientes cn pueden obtenerse a partir de los coeficientes an, bn como ya se dijo, o bien:Para n = 0, 1, 2, 3, ...

26. 26f(t)1t. . . -T/2 0T/2 T . . .-1Ejemplo. Encontrar la forma compleja de la serie de Fourier para la función ya tratada:Solución 1. Como ya se calcularon los coeficientes de la forma trigonométrica (an y bn), que eran an= 0 para todo n y

27. 270Entonces la serie compleja de Fourier queda:

28. 28Solución 2. También podemos calcular los coeficientes cn mediante la integral:

29. 29Como w0T = 2p y :que coincide con el resultado ya obtenido.

30. 30Actividad 3Calcular la serie de Fourier de la función de Heaviside, usando la forma compleja,

31. 31d(t)d(t)f3(t)f2(t)tLa función impulso o delta de Diracf1(t)tPodemos pensar en la delta de Dirac como el límite de una serie de funciones:

32. 32d(t)tPropiedades de la función d

33. 33Calcular la serie de Fourier de d(x):

34. 34Calcular la serie de Fourier de d(x):Para todas las x ≠ 0 la función delta vale 0

35. 35

36. 36

37. 37

38. 38

39. 39

40. 40

41. 41

42. 42

43. 43

44. 44