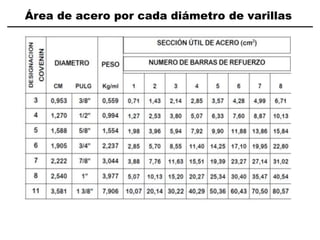
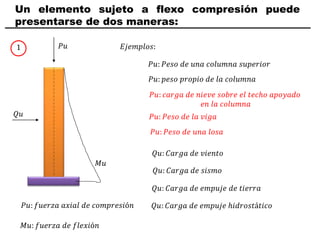
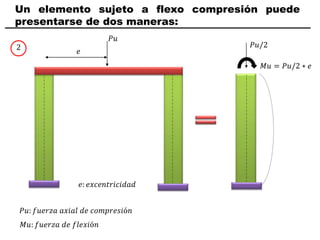
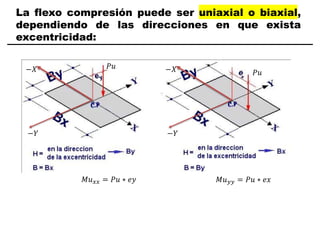
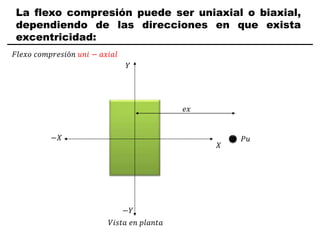
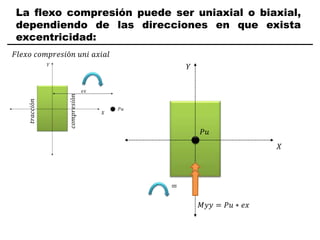
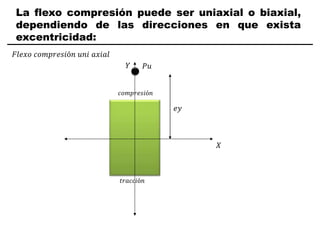
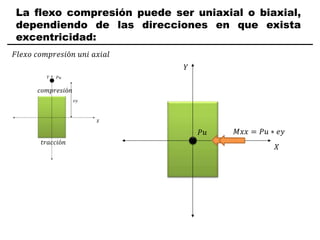
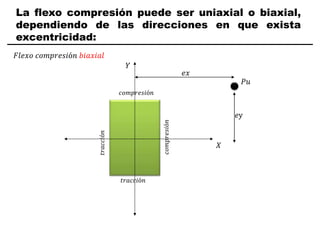
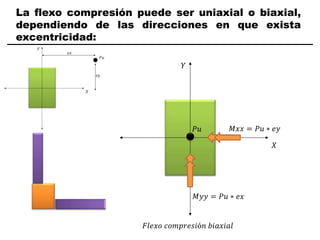
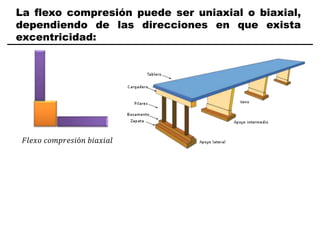
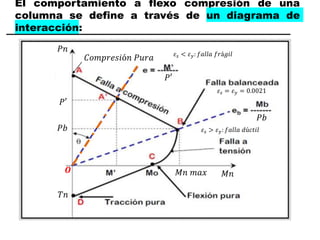
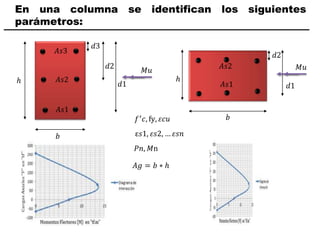
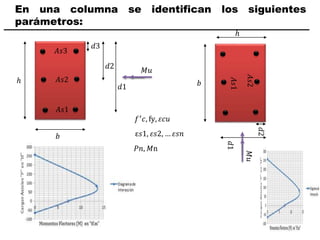
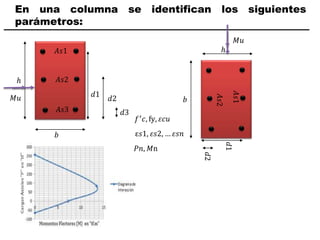
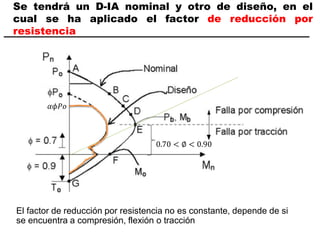
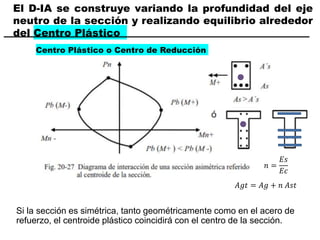
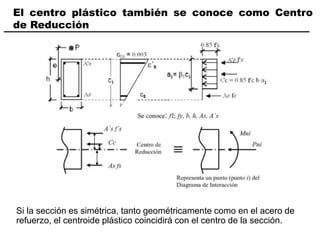
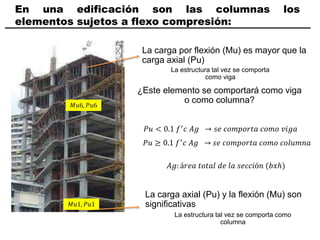
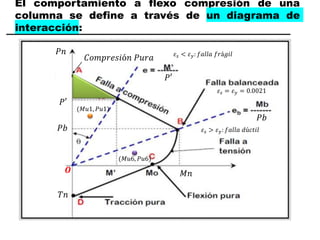
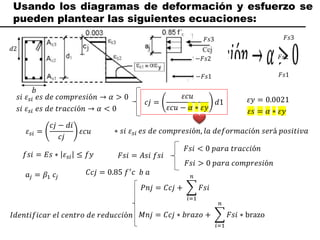
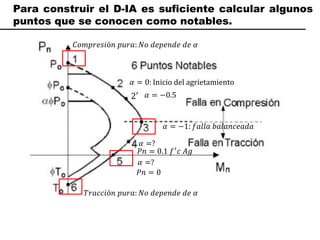
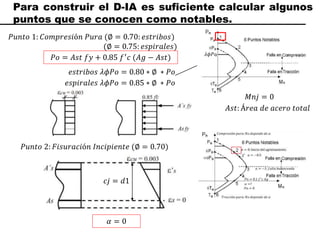
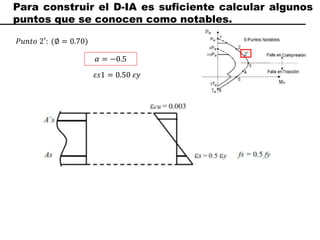
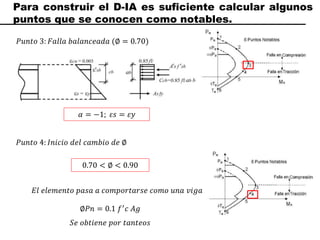
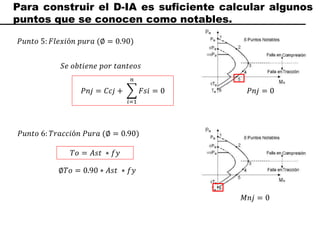
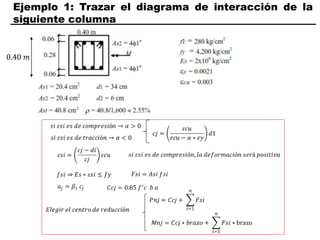
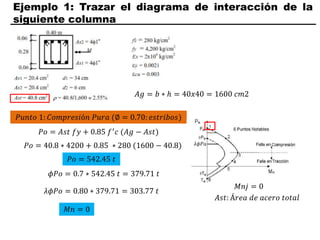
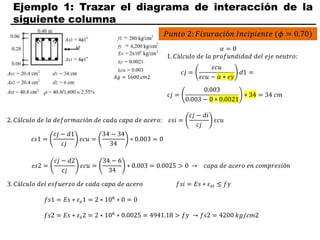
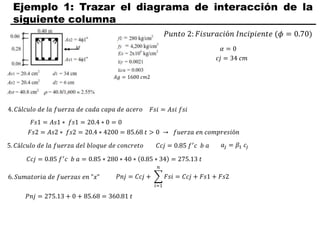
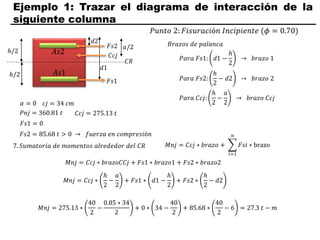
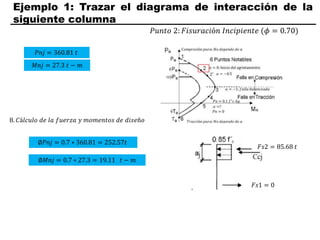
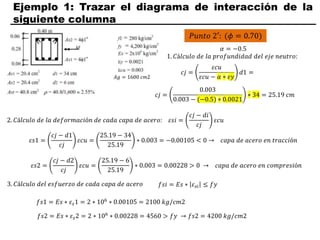
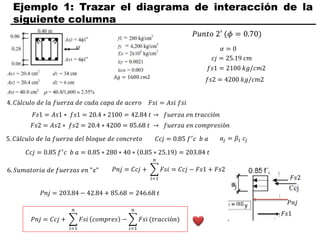
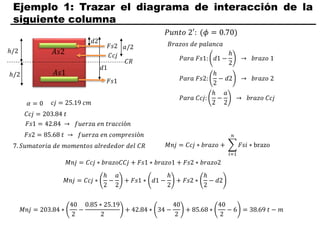
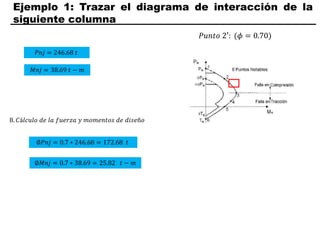
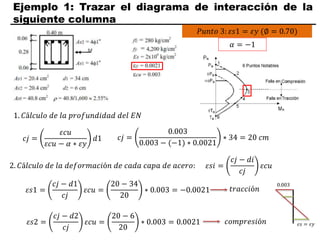
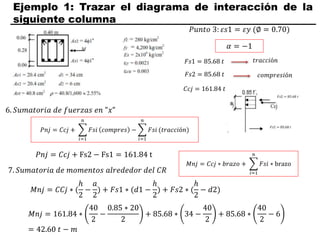
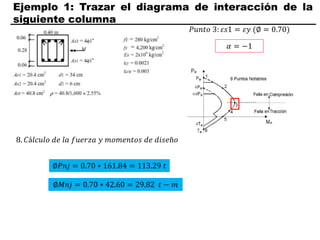
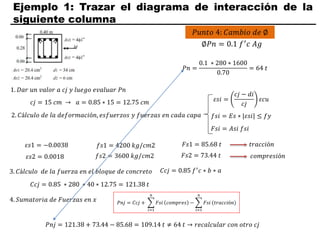
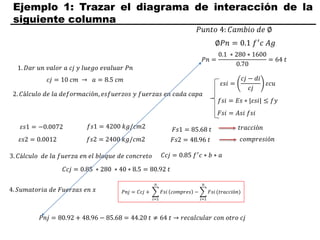
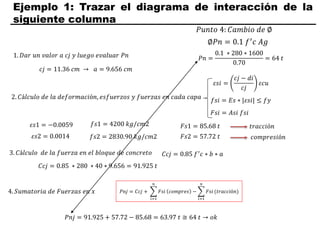
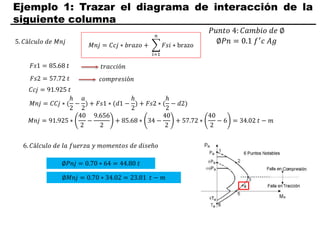
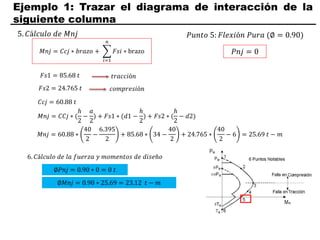
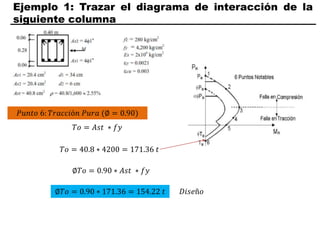
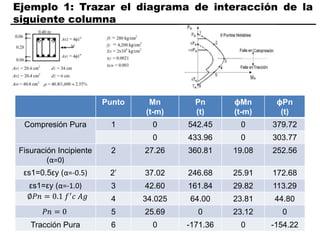
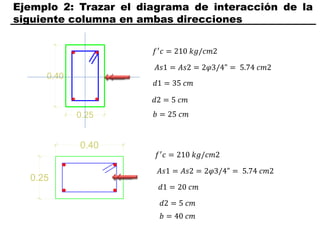
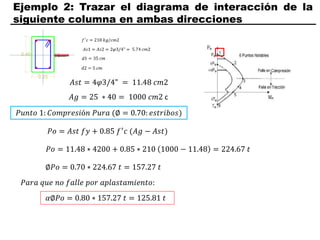
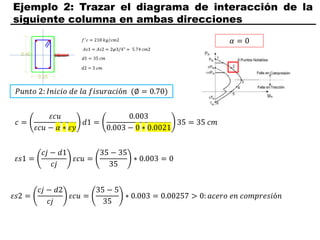
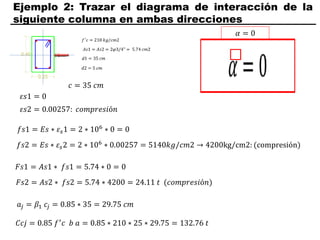
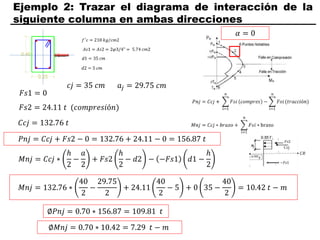
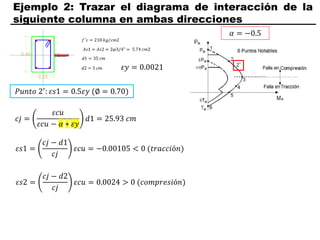
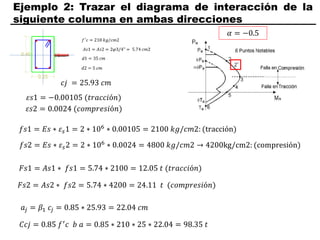
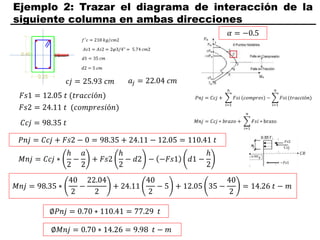
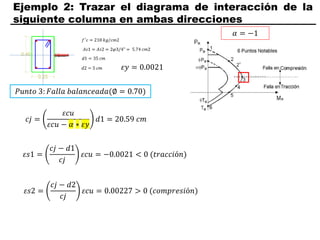
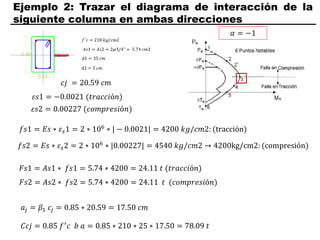
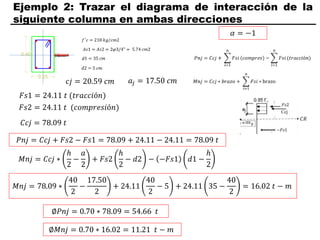
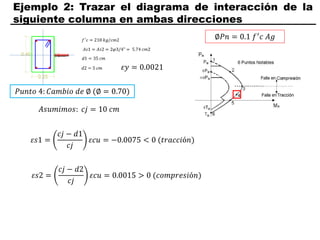
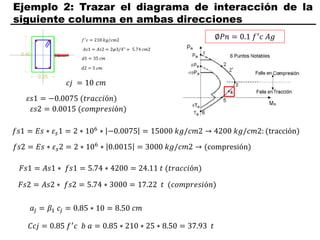
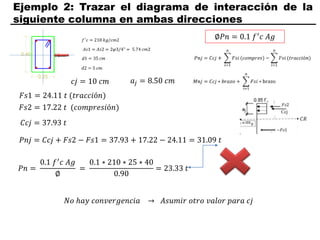
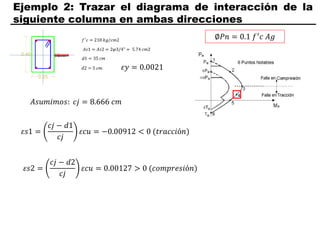
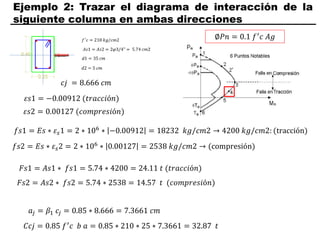
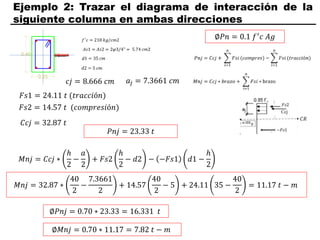
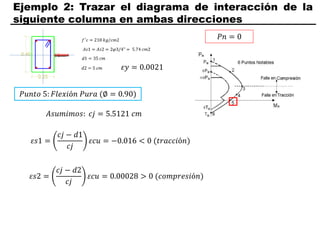
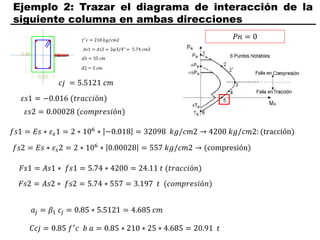
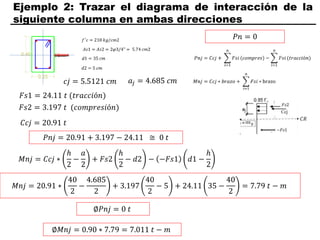
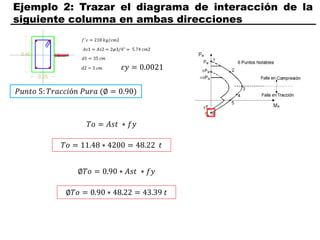
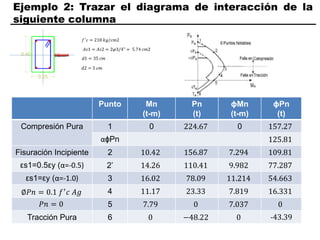
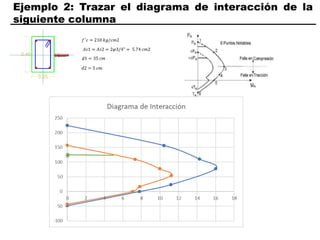
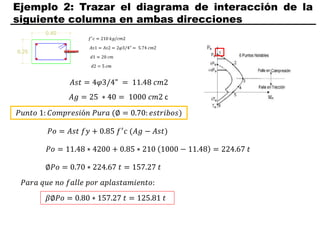
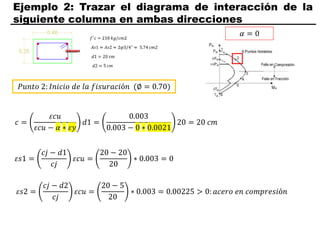
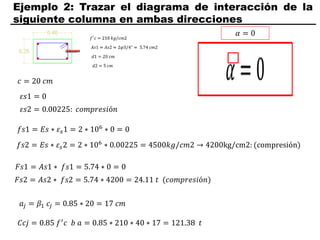
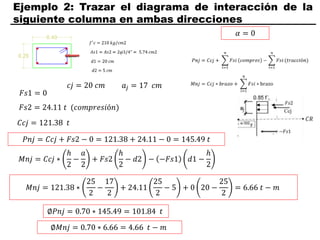
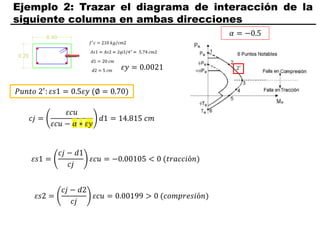
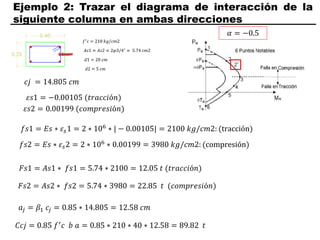
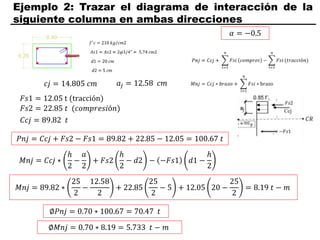
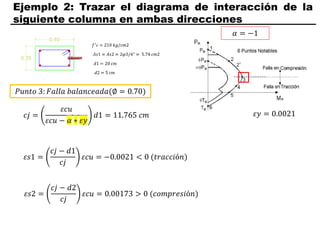
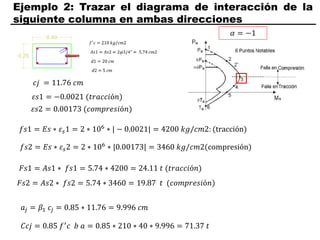
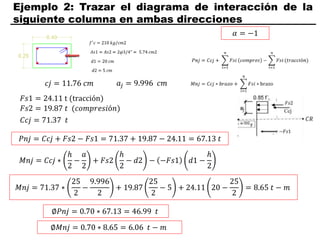
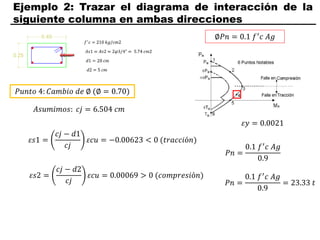
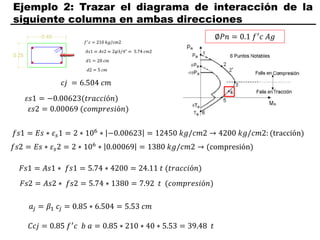
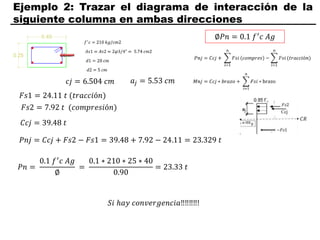
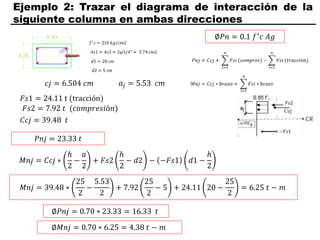
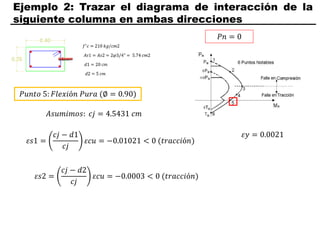
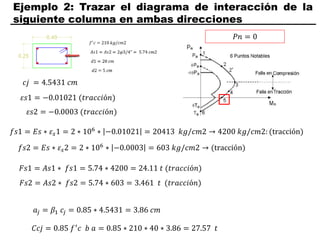
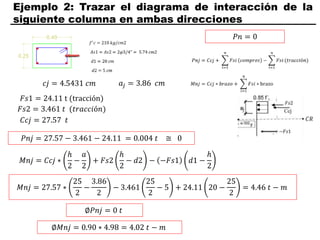
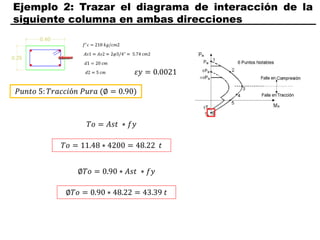
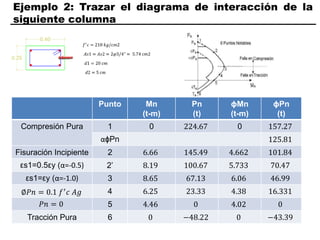
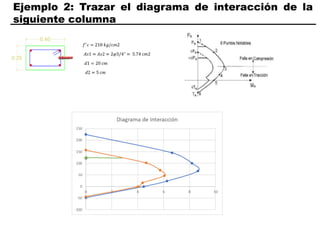
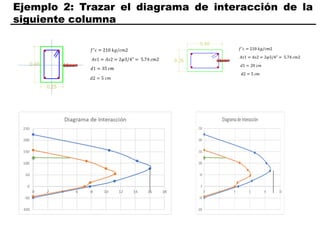
El documento describe los conceptos fundamentales de flexo compresión en elementos de concreto armado. Flexo compresión se refiere a la combinación de fuerzas de flexión y compresión que actúan sobre un elemento. Esto puede ocurrir de manera uniaxial o biaxial dependiendo de la dirección de las fuerzas. El comportamiento de un elemento sujeto a flexo compresión se define a través de un diagrama de interacción. Este diagrama depende de factores como la resistencia del concreto, la geometría de la sección y el área